第十五讲最短路线问题.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：0.07M 资料格式：doc 举报版权申诉

第1页 / 共5页

第2页 / 共5页

第3页 / 共5页

第4页 / 共5页

第5页 / 共5页

文本预览

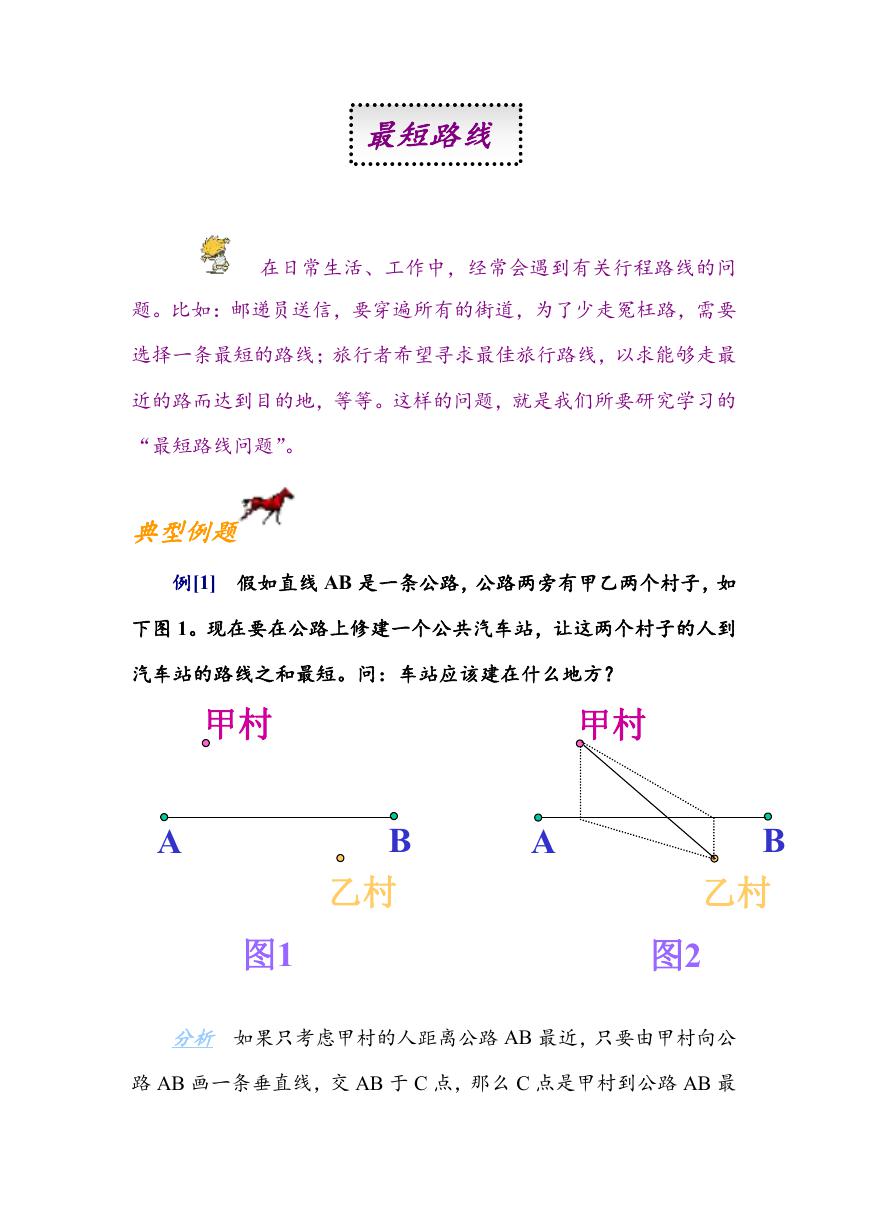
最短路线在日常生活、工作中，经常会遇到有关行程路线的问题。比如：邮递员送信，要穿遍所有的街道，为了少走冤枉路，需要选择一条最短的路线；旅行者希望寻求最佳旅行路线，以求能够走最近的路而达到目的地，等等。这样的问题，就是我们所要研究学习的 “最短路线问题”。典型例题例[1] 假如直线 AB 是一条公路，公路两旁有甲乙两个村子，如下图 1。现在要在公路上修建一个公共汽车站，让这两个村子的人到汽车站的路线之和最短。问：车站应该建在什么地方？甲村甲村 A B 乙村 A 图1 B 乙村图2 分析如果只考虑甲村的人距离公路 AB 最近，只要由甲村向公路 AB 画一条垂直线，交 AB 于 C 点，那么 C 点是甲村到公路 AB 最

近的点，但是乙村到 C 点就较远了。反过来，由乙村向公路 AB 画垂线，交 AB 于 D 点，那么 D 点是乙村到公路 AB 最近的点。但是这时甲村到公路 AB 的 D 点又远了。因为本题要求我们在公路 AB 上取的建站点，能够兼顾甲村和乙村的人到这个车站来不走冤枉路（既路程之和最短），根据我们的经验：两个地点之间走直线最近，所以，只要在甲村乙村间连一条直线，这条直线与公路 AB 交点 P，就是所求的公共汽车站的建站点了（图 2）。解用直线把甲村、乙村连起来。因为甲村乙村在公路的两侧，所以这条连线必与公路 AB 有一个交点，设这个交点为 P，那么在 P 点建立汽车站，就能使甲村乙村的人到汽车站所走的路程之和最短。例[2] 一个邮递员投送信件的街道如图 3 所示，图上数字表示各段街道的千米数。他从邮局出发，要走遍各街道，最后回到邮局。问：走什么样的路线最合理？全程要走多少千米？ 1 2 4 2 1 3 分析选择最短的路线最合理。那么，什么路线最短呢？一笔画路线应该是最短的。邮递员从邮局出发，还要回到邮局，按一笔画问

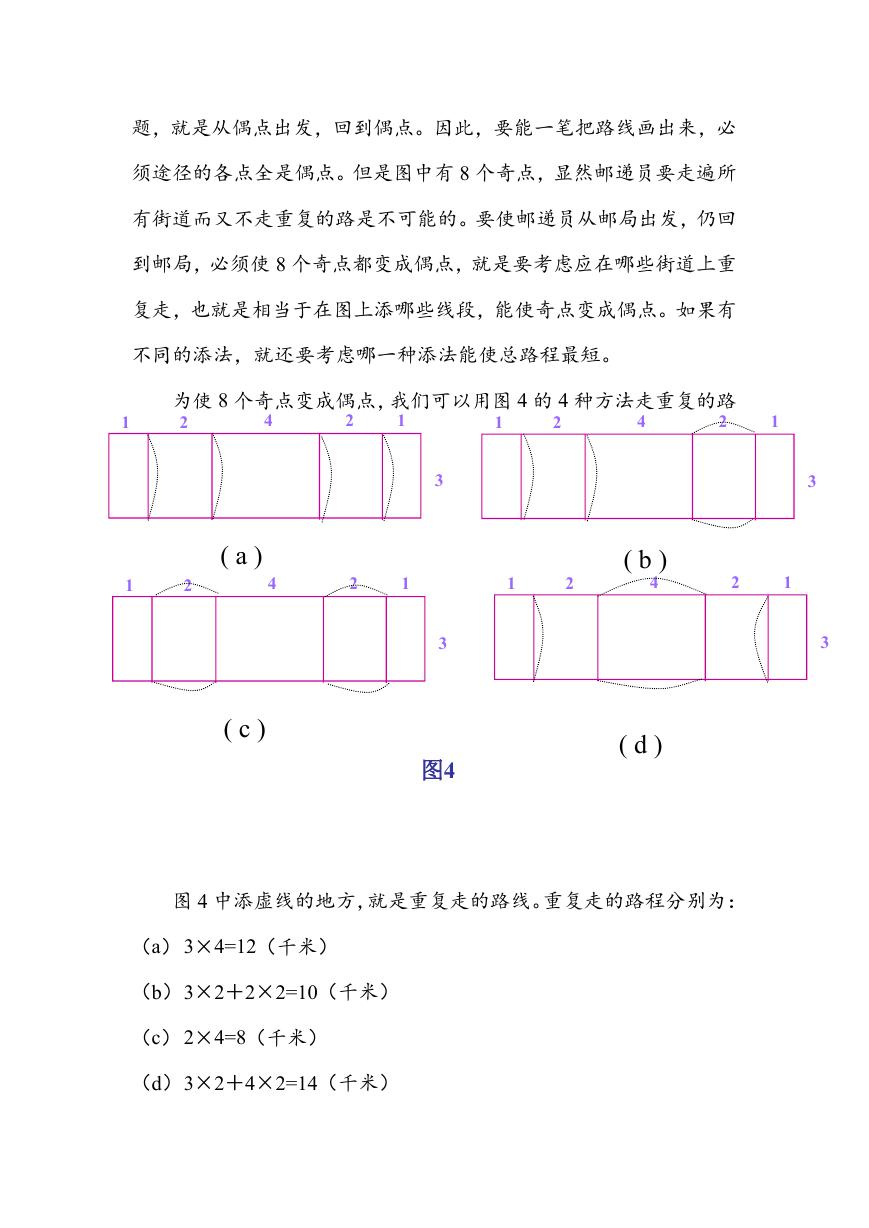
题，就是从偶点出发，回到偶点。因此，要能一笔把路线画出来，必须途径的各点全是偶点。但是图中有 8 个奇点，显然邮递员要走遍所有街道而又不走重复的路是不可能的。要使邮递员从邮局出发，仍回到邮局，必须使 8 个奇点都变成偶点，就是要考虑应在哪些街道上重复走，也就是相当于在图上添哪些线段，能使奇点变成偶点。如果有不同的添法，就还要考虑哪一种添法能使总路程最短。为使 8 个奇点变成偶点，我们可以用图 4 的 4 种方法走重复的路 2 2 4 4 2 1 1 2 1 线。 ( a ) 4 1 2 2 1 ( c ) 3 3 图4 1 3 1 2 ( b ) 4 2 1 3 ( d ) 图 4 中添虚线的地方，就是重复走的路线。重复走的路程分别为：（a）3×4=12（千米）（b）3×2＋2×2=10（千米）（c）2×4=8（千米）（d）3×2＋4×2=14（千米）

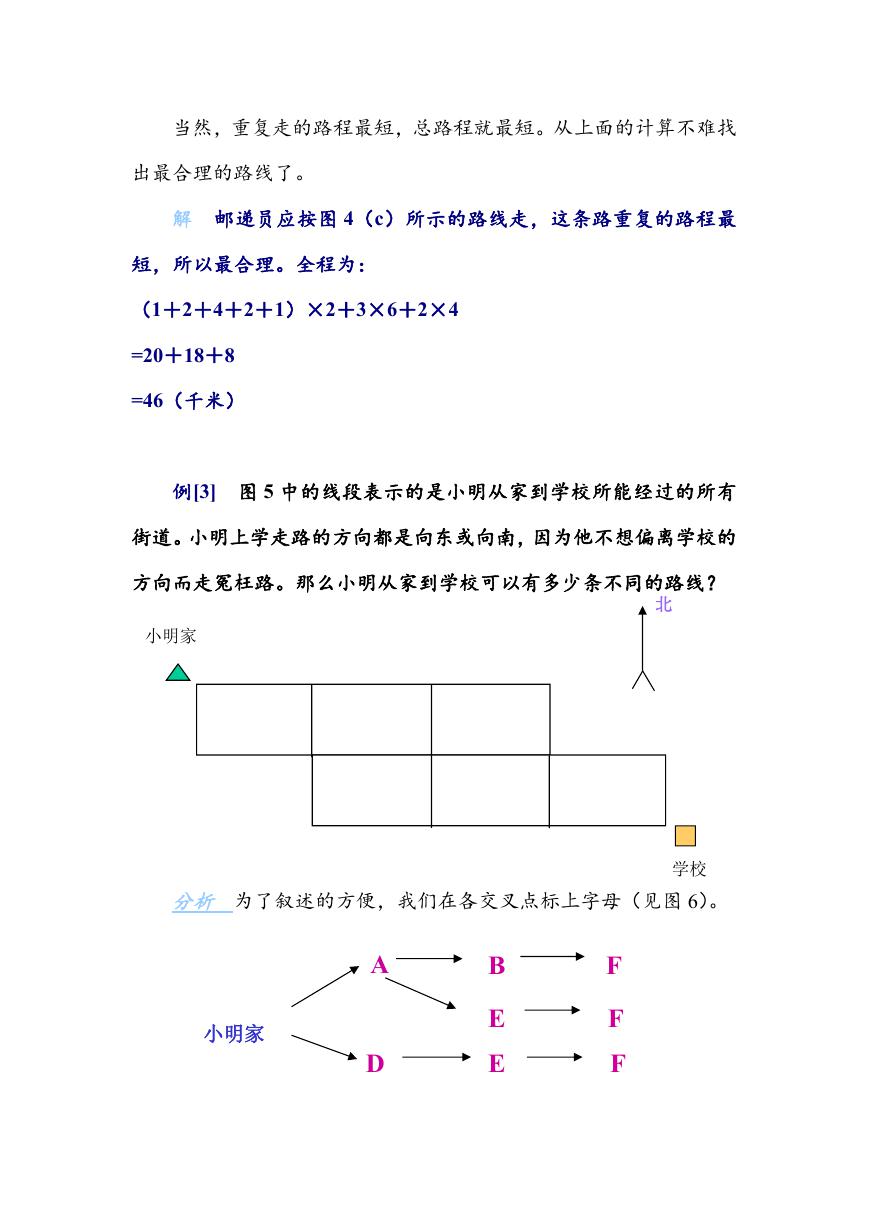
当然，重复走的路程最短，总路程就最短。从上面的计算不难找出最合理的路线了。解邮递员应按图 4（c）所示的路线走，这条路重复的路程最短，所以最合理。全程为：（1＋2＋4＋2＋1）×2＋3×6＋2×4 =20＋18＋8 =46（千米）例[3] 图 5 中的线段表示的是小明从家到学校所能经过的所有街道。小明上学走路的方向都是向东或向南，因为他不想偏离学校的方向而走冤枉路。那么小明从家到学校可以有多少条不同的路线？北小明家分析为了叙述的方便，我们在各交叉点标上字母（见图 6）。学校小明家 A D B E E F F F

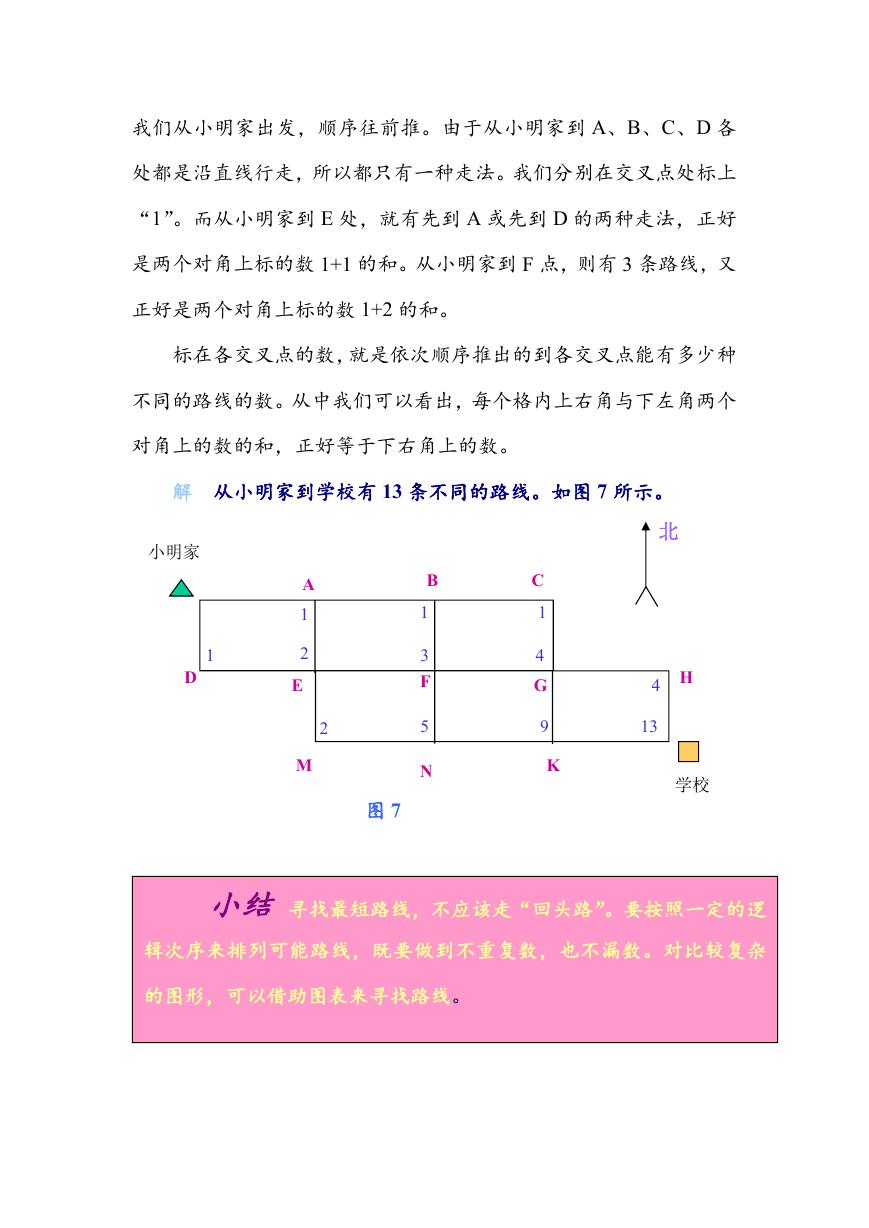
我们从小明家出发，顺序往前推。由于从小明家到 A、B、C、D 各处都是沿直线行走，所以都只有一种走法。我们分别在交叉点处标上 “1”。而从小明家到 E 处，就有先到 A 或先到 D 的两种走法，正好是两个对角上标的数 1+1 的和。从小明家到 F 点，则有 3 条路线，又正好是两个对角上标的数 1+2 的和。标在各交叉点的数，就是依次顺序推出的到各交叉点能有多少种不同的路线的数。从中我们可以看出，每个格内上右角与下左角两个对角上的数的和，正好等于下右角上的数。解从小明家到学校有 13 条不同的路线。如图 7 所示。小明家 1 D A 1 2 E 2 M B 1 3 F 5 N 图 7 C 1 4 G 9 K 北 H 4 13 学校小结寻找最短路线，不应该走“回头路”。要按照一定的逻辑次序来排列可能路线，既要做到不重复数，也不漏数。对比较复杂的图形，可以借助图表来寻找路线。

分享到：

赞收藏

资料库

第十五讲最短路线问题.doc

相关推荐

小学奥数

热门标签

最新资料