4-5-1 长方体与正方体（一）.学生版.doc-资料库

第1页 / 共20页

第2页 / 共20页

第3页 / 共20页

第4页 / 共20页

第5页 / 共20页

第6页 / 共20页

第7页 / 共20页

第8页 / 共20页

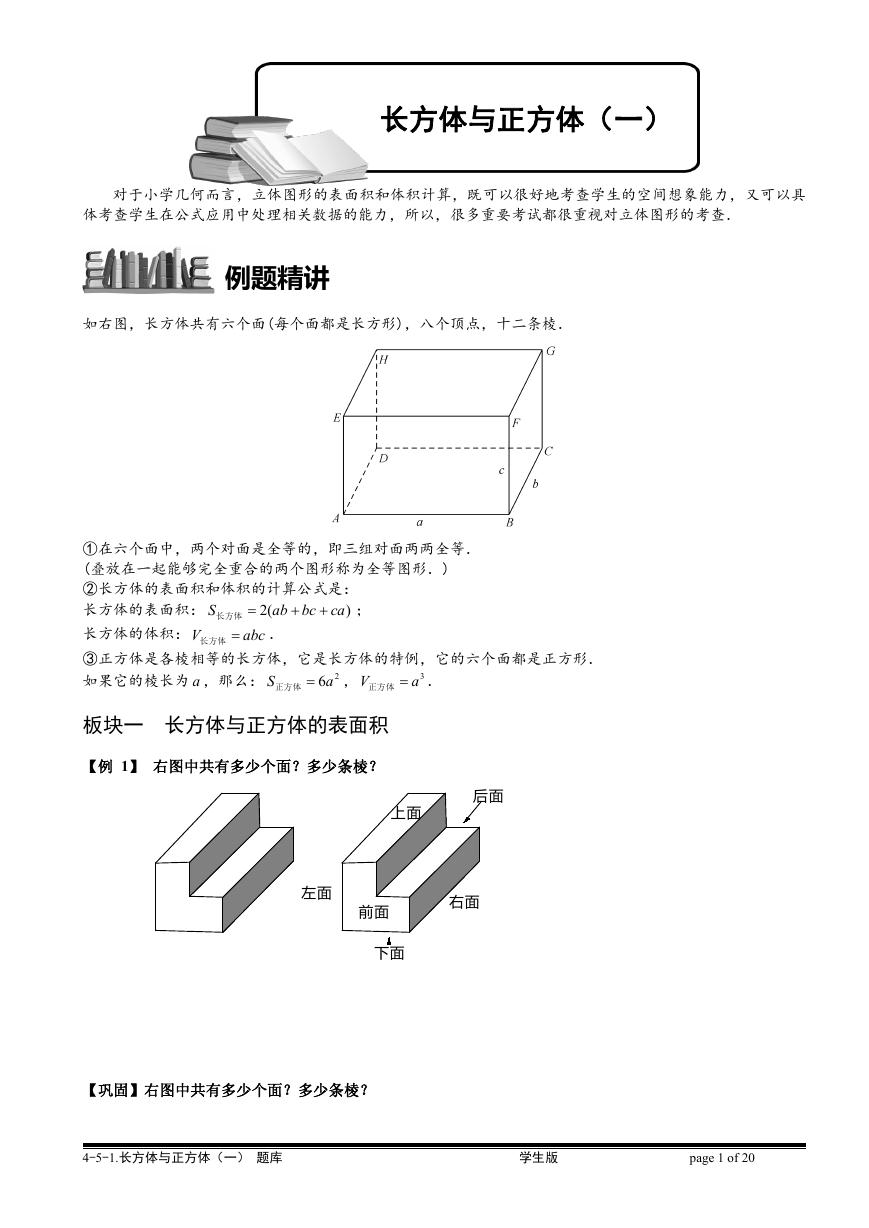
长方体与正方体（一）对于小学几何而言，立体图形的表面积和体积计算，既可以很好地考查学生的空间想象能力，又可以具体考查学生在公式应用中处理相关数据的能力，所以，很多重要考试都很重视对立体图形的考查．例题精讲如右图，长方体共有六个面(每个面都是长方形)，八个顶点，十二条棱．   长方体 ①在六个面中，两个对面是全等的，即三组对面两两全等． (叠放在一起能够完全重合的两个图形称为全等图形．) ②长方体的表面积和体积的计算公式是： ) 长方体的表面积：长方体的体积：V ③正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形．如果它的棱长为 a ，那么： 2( ab bc  abc ． 26 a 3 a  ca ；， V 正方体 S 正方体 S 长方体．板块一长方体与正方体的表面积【例 1】右图中共有多少个面？多少条棱？后面上面左面前面下面右面【巩固】右图中共有多少个面？多少条棱？ 4-5-1.长方体与正方体（一）题库学生版 page 1 of 20

【例 2】如右图，在一个棱长为 10 的立方体上截取一个长为 8，宽为 3，高为 2 的小长方体，那么新的几何体的表面积是多少？【巩固】在一个棱长为 50 厘米的正方体木块，在它的八个角上各挖去一个棱长为 5 厘米的小正方体，问剩下的立体图形的表面积是多少？【例 3】如右图，有一个边长是 5 的立方体，如果它的左上方截去一个边分别是 5，3，2 的长方体，那么它的表面积减少了多少? 【例 4】如图，有一个边长是 5 的立方体，如果它的左上方截去一个边分别是 5，3，2 的长方体，那么它的表面积减少了百分之几? 4-5-1.长方体与正方体（一）题库学生版 page 2 of 20

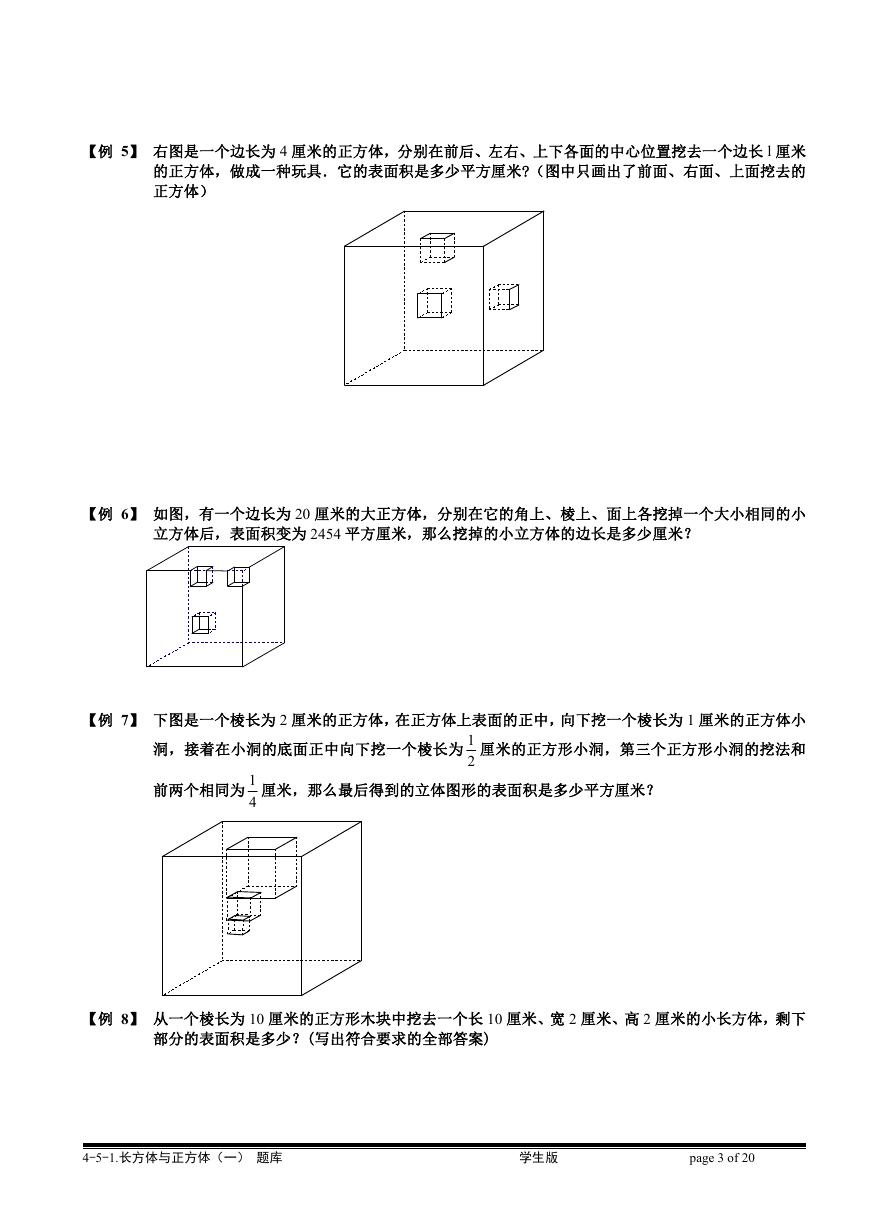
【例 5】右图是一个边长为 4 厘米的正方体，分别在前后、左右、上下各面的中心位置挖去一个边长 l 厘米的正方体，做成一种玩具．它的表面积是多少平方厘米?（图中只画出了前面、右面、上面挖去的正方体）【例 6】如图，有一个边长为 20 厘米的大正方体，分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后，表面积变为 2454 平方厘米，那么挖掉的小立方体的边长是多少厘米？【例 7】下图是一个棱长为 2 厘米的正方体，在正方体上表面的正中，向下挖一个棱长为 1 厘米的正方体小厘米的正方形小洞，第三个正方形小洞的挖法和洞，接着在小洞的底面正中向下挖一个棱长为 1 2 前两个相同为 1 4 厘米，那么最后得到的立体图形的表面积是多少平方厘米？【例 8】从一个棱长为 10 厘米的正方形木块中挖去一个长 10 厘米、宽 2 厘米、高 2 厘米的小长方体，剩下部分的表面积是多少？(写出符合要求的全部答案) 4-5-1.长方体与正方体（一）题库学生版 page 3 of 20

【例 9】一个正方体木块，棱长是 15．从它的八个顶点处各截去棱长分别是 1、2、3、4、5、6、7、8 的小正方体．这个木块剩下部分的表面积最少是多少？【例 10】从一个长 8 厘米、宽 7 厘米、高 6 厘米的长方体中截下一个最大的正方体(如下图)，剩下部分的表面积之和是平方厘米． 8 6 6 6 7 【巩固】一个长、宽、高分别为 21 厘米、15 厘米、12 厘米的长方形，现从它的上面尽可能大的切下一个正方体，然后从剩余的部分再尽可能大的切下一个正方体，最后再从第二次剩余的部分尽可能大的切下一个正方体，剩下的体积是多少平方厘米？【例 11】一个正方体木块，棱长是 1 米，沿着水平方向将它锯成 2 片，每片又锯成 3 长条，每条又锯成 4 小块，共得到大大小小的长方体 24 块，那么这 24 块长方体的表面积之和是多少？ 4-5-1.长方体与正方体（一）题库学生版 page 4 of 20

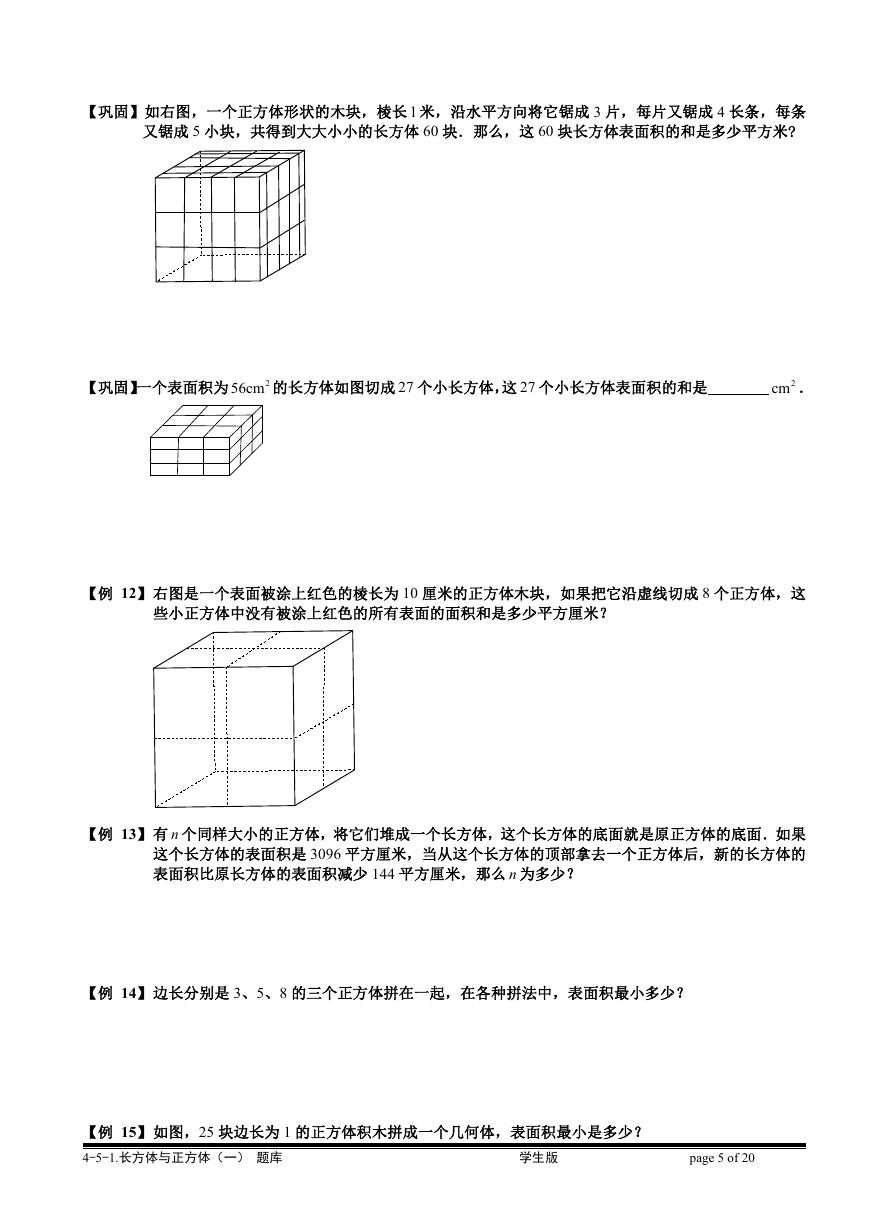
【巩固】如右图，一个正方体形状的木块，棱长 l 米，沿水平方向将它锯成 3 片，每片又锯成 4 长条，每条又锯成 5 小块，共得到大大小小的长方体 60 块．那么，这 60 块长方体表面积的和是多少平方米? 【巩固】一个表面积为 56cm 的长方体如图切成 27 个小长方体，这 27 个小长方体表面积的和是 2 2cm ．【例 12】右图是一个表面被涂上红色的棱长为 10 厘米的正方体木块，如果把它沿虚线切成 8 个正方体，这些小正方体中没有被涂上红色的所有表面的面积和是多少平方厘米？【例 13】有 n 个同样大小的正方体，将它们堆成一个长方体，这个长方体的底面就是原正方体的底面．如果这个长方体的表面积是 3096 平方厘米，当从这个长方体的顶部拿去一个正方体后，新的长方体的表面积比原长方体的表面积减少 144 平方厘米，那么 n 为多少？【例 14】边长分别是 3、5、8 的三个正方体拼在一起，在各种拼法中，表面积最小多少？【例 15】如图，25 块边长为 1 的正方体积木拼成一个几何体，表面积最小是多少？ 4-5-1.长方体与正方体（一）题库学生版 page 5 of 20

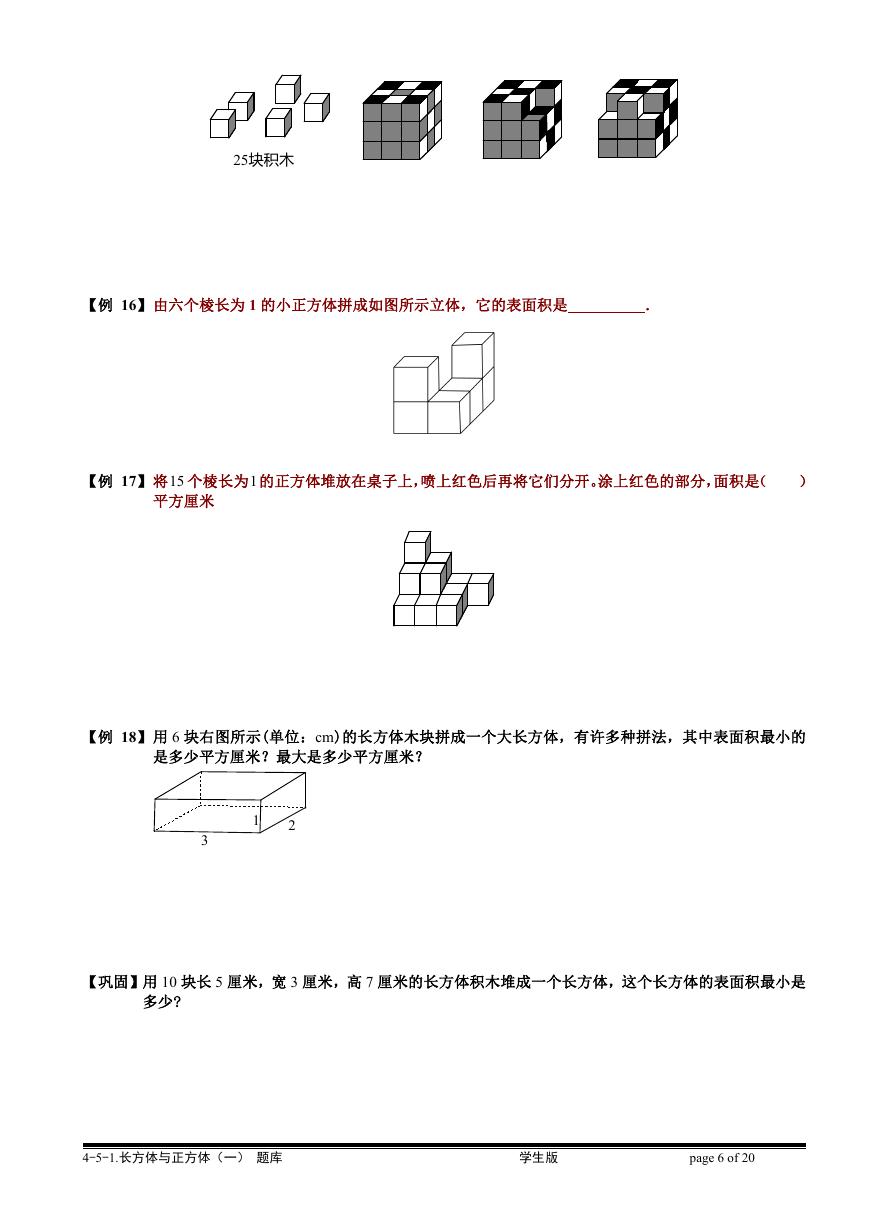
25块积木【例 16】由六个棱长为 1 的小正方体拼成如图所示立体，它的表面积是．【例 17】将15 个棱长为1 的正方体堆放在桌子上，喷上红色后再将它们分开。涂上红色的部分，面积是（）平方厘米【例 18】用 6 块右图所示(单位：cm)的长方体木块拼成一个大长方体，有许多种拼法，其中表面积最小的是多少平方厘米？最大是多少平方厘米？ 1 2 3 【巩固】用 10 块长 5 厘米，宽 3 厘米，高 7 厘米的长方体积木堆成一个长方体，这个长方体的表面积最小是多少? 4-5-1.长方体与正方体（一）题库学生版 page 6 of 20

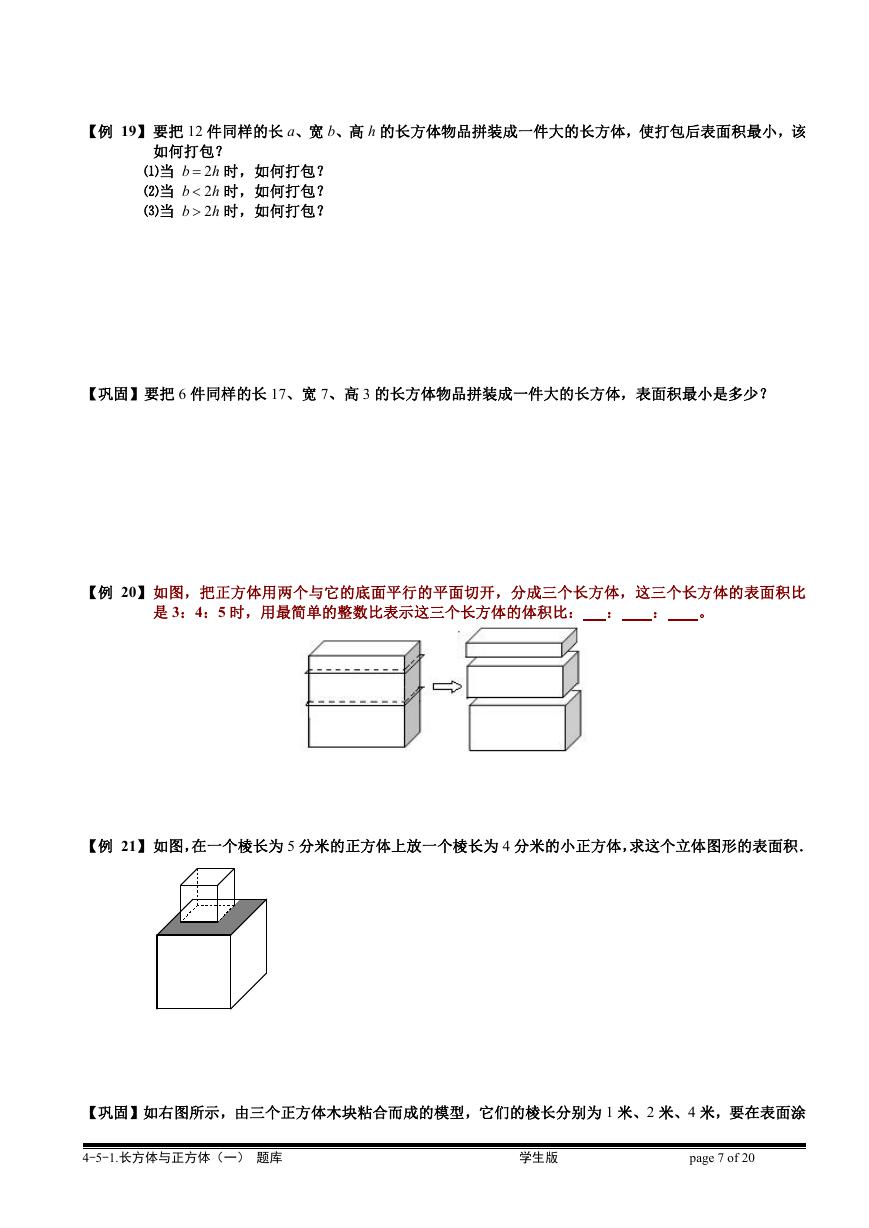
【例 19】要把 12 件同样的长 a、宽 b、高 h 的长方体物品拼装成一件大的长方体，使打包后表面积最小，该如何打包？ ⑴当 b  2h 时，如何打包？ ⑵当 b  2h 时，如何打包？ ⑶当 b  2h 时，如何打包？【巩固】要把 6 件同样的长 17、宽 7、高 3 的长方体物品拼装成一件大的长方体，表面积最小是多少？【例 20】如图，把正方体用两个与它的底面平行的平面切开，分成三个长方体，这三个长方体的表面积比是 3：4：5 时，用最简单的整数比表示这三个长方体的体积比：：：。【例 21】如图，在一个棱长为 5 分米的正方体上放一个棱长为 4 分米的小正方体，求这个立体图形的表面积．【巩固】如右图所示，由三个正方体木块粘合而成的模型，它们的棱长分别为 1 米、2 米、4 米，要在表面涂 4-5-1.长方体与正方体（一）题库学生版 page 7 of 20

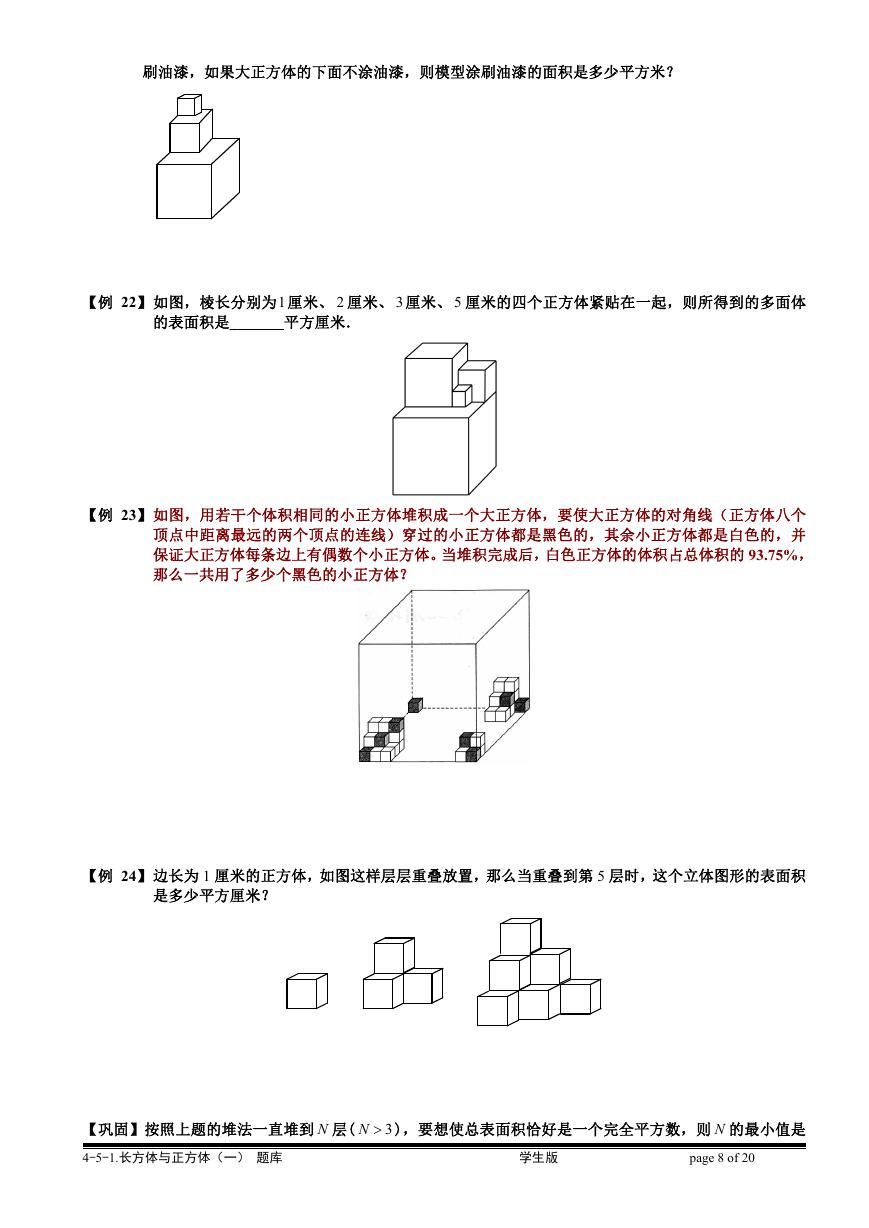
刷油漆，如果大正方体的下面不涂油漆，则模型涂刷油漆的面积是多少平方米？【例 22】如图，棱长分别为1 厘米、 2 厘米、 3 厘米、 5 厘米的四个正方体紧贴在一起，则所得到的多面体的表面积是_______平方厘米．【例 23】如图，用若干个体积相同的小正方体堆积成一个大正方体，要使大正方体的对角线（正方体八个顶点中距离最远的两个顶点的连线）穿过的小正方体都是黑色的，其余小正方体都是白色的，并保证大正方体每条边上有偶数个小正方体。当堆积完成后，白色正方体的体积占总体积的 93.75%，那么一共用了多少个黑色的小正方体？【例 24】边长为 1 厘米的正方体，如图这样层层重叠放置，那么当重叠到第 5 层时，这个立体图形的表面积是多少平方厘米？【巩固】按照上题的堆法一直堆到 N 层( 4-5-1.长方体与正方体（一）题库 3N  )，要想使总表面积恰好是一个完全平方数，则 N 的最小值是学生版 page 8 of 20

资料库

4-5-1 长方体与正方体（一）.学生版.doc

相关推荐

小学奥数

热门标签

最新资料