5-1-3-2 数阵图（二）.学生版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：0.99M 资料格式：doc 举报版权申诉

第1页 / 共5页

第2页 / 共5页

第3页 / 共5页

第4页 / 共5页

第5页 / 共5页

文本预览

5-1-3-2.数阵图教学目标 1. 了解数阵图的种类 2. 学会一些解决数阵图的解题方法 3. 能够解决和数论相关的数阵图问题知识点拨 . 一、数阵图定义及分类： 1. 定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图. 2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图. 3. 二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手：第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．例题精讲复合型数阵图【例 1】由数字 1、2、3 组成的不同的两位数共有 9 个，老师将这 9 个数写在一个九宫格上，让同学选数，每个同学可以从中选 5 个数来求和．小刚选的 5 个数的和是 120，小明选的 5 个数的和是 111．如果两人选的数中只有一个是相同的，那么这个数是_____________．【例 2】如图 1，圆圈内分别填有 1，2，……，7 这 7 个数。如果 6 个三角形的顶点处圆圈内的数字的和是 64，那么，中间圆圈内填入的数是。 5-1-3-2.数阵图.题库学生版 page 1 of 5

【例 3】如下图（1）所示，在每个小圆圈内填上一个数，使得每一条直线上的三个数的和都等于大圆圈上三个数的和. 【例 4】请你将数字 1、2、3、4、5、6、7 填在下面图（1）所示的圆圈内，使得每个圆圈上的三个数之和与每条直线上的三个数之和相等.应怎样填？【例 5】在左下图的每个圆圈中填上一个数，各数互不相等，每个圆圈有 3 个相邻(即有线段相连的圆圈)的圆圈。将左下图中每个圆圈中的数改为 3 个相邻圆圈所填数的平均值，便得到右下图。如果左下图中已有一个数 1，请填出左下图中的其它数，使得右下图中的数都是自然数。【例 6】将 1 至 8 这八个自然数分别填入图中的正方体的八个顶点处的  内，并使每个面上的四个  内的数字之和都相等。求与填入数字 1 的  有线段相连的三个  内的数的和的最大值。【例 7】将自然数1 到11分别填在右图的圆圈内，使得图中每条直线上的三个圆圈内的数的和相等． 5-1-3-2.数阵图.题库学生版 page 2 of 5

b 18- b - c c 12- b b+ -6 c 12- c + c d -6 18- - c d 6 12- d d 1 11 6 8 4 3 5 10 9 7 2 【例 8】在下图中，在每个圆圈中填入一个数，使每条直线上所有圆圈中数的和都是 234，那么标有★的圆圈中所填的数是_____________．【例 9】请将 1，2，3，…，10 这 10 个自然数填入图中的 10 个小圆圈内，使得图中的 10 条直线上圆圈内数字之和都相等．那么乘积 A B C    ？ A B C 【例 10】下图中有 11 条直线．请将 1 至 11 这 11 个数分别填在 11 个圆圈里，使每一条直线上所有数的和相等．求这个相等的和以及标有*的圆圈中所填的数． ﹡ 【例 11】 “美妙的数学花园”这 7 个字各代表 1~7 中的一个数，并且每个圆中 4 个数的和都是 15。如果学比 5-1-3-2.数阵图.题库学生版 page 3 of 5

美大，美比园大，那么，园表示。【例 12】图 2 中的五个问号分别表示五个连续的自然数，它们的和等于 130，三角形内两个数的和等于 53，圆内三个数的和等于 79，正方形内两个数的和等于 50。那么，从左向右，这五个问号依次是【例 13】右图是大家都熟悉的奥林匹克五环标志．请将1 9 分别填入五个圆相互分割的九个部分，并且使每个圆环内的数字之和都相等．【例 14】2008 年奥运会在北京举行。“奥”、“运”、 “会”、“北”、“京”这五个汉字代表五个连续的自然数，将其分别填在五环图案的五个环内，满足“奥”+“运”+“会”=“北”+“京”。这五个自然数的和最大是。【例 15】如图， A ， B ， C ， D ， E ， F ， G ， H ， I 代表九个各不相同的正整数，且每个圆中所填数的和都等于 2008 。这九个数总和最小为。【例 16】如图， A ， B ，C ， D ， E ， F ，G ， H ， I 代表九个各不相同的正整数， A ， B ，C ， D ， E ， 5-1-3-2.数阵图.题库学生版 page 4 of 5

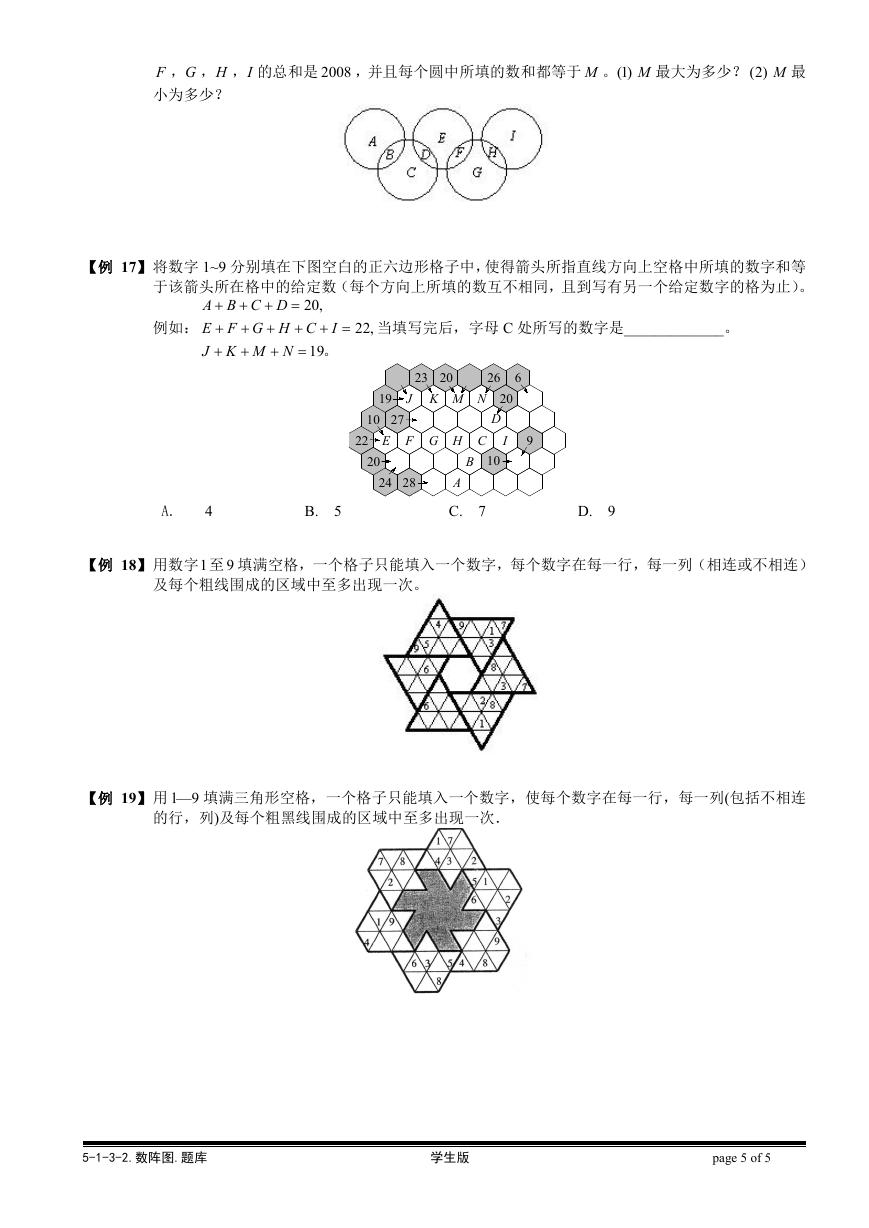
F ，G ，H ，I 的总和是 2008 ，并且每个圆中所填的数和都等于 M 。(1) M 最大为多少？ (2) M 最小为多少？【例 17】将数字 1~9 分别填在下图空白的正六边形格子中，使得箭头所指直线方向上空格中所填的数字和等于该箭头所在格中的给定数（每个方向上所填的数互不相同，且到写有另一个给定数字的格为止）。 A B C D  E F G H C I  J K M N  。          20, 19 例如：   22, 当填写完后，字母 C 处所写的数字是_____________。 23 20 J F K G 19 10 27 22 E 20 24 28 M H A C. 26 6 20 D I 9 N C B 10 7 D. 9 A. 4 B. 5 【例 18】用数字1 至 9 填满空格，一个格子只能填入一个数字，每个数字在每一行，每一列（相连或不相连）及每个粗线围成的区域中至多出现一次。【例 19】用 l—9 填满三角形空格，一个格子只能填入一个数字，使每个数字在每一行，每一列(包括不相连的行，列)及每个粗黑线围成的区域中至多出现一次． 5-1-3-2.数阵图.题库学生版 page 5 of 5

分享到：

赞收藏

资料库

5-1-3-2 数阵图（二）.学生版.doc

相关推荐

小学奥数

热门标签

最新资料