7-7-1 容斥原理之重叠问题（一）.学生版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：0.91M 资料格式：doc 举报版权申诉

第1页 / 共7页

第2页 / 共7页

第3页 / 共7页

第4页 / 共7页

第5页 / 共7页

第6页 / 共7页

第7页 / 共7页

文本预览

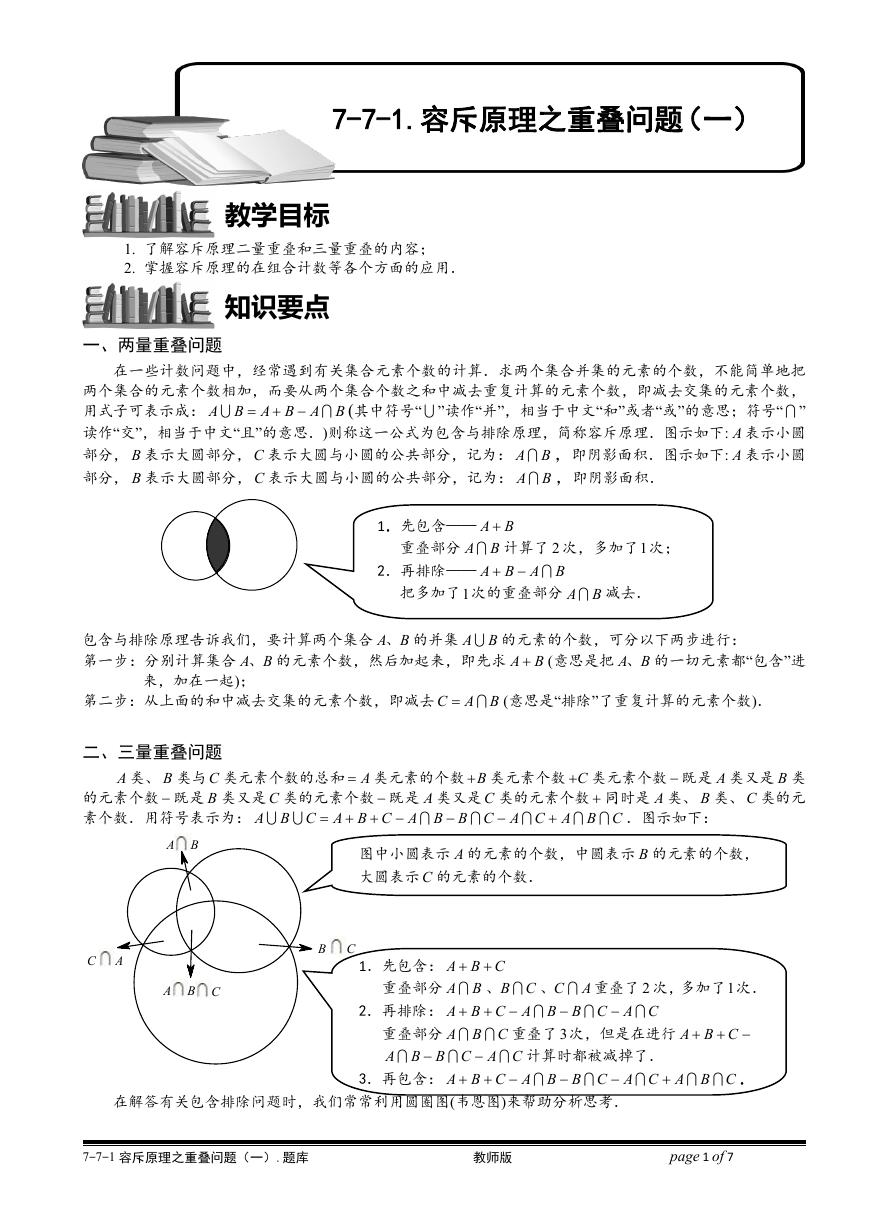
7-7-1.容斥原理之重叠问题（一）教学目标 1. 了解容斥原理二量重叠和三量重叠的内容； 2. 掌握容斥原理的在组合计数等各个方面的应用．知识要点一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，  (其中符号“  ”读作“并”，相当于中文“和”或者“或”的意思；符号“  ” 用式子可表示成： A B A B A B 读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下: A 表示小圆部分， B 表示大圆部分， C 表示大圆与小圆的公共部分，记为： A B ，即阴影面积．图示如下: A 表示小圆部分， B 表示大圆部分， C 表示大圆与小圆的公共部分，记为： A B ，即阴影面积．     1．先包含—— A B 重叠部分 A B 计算了 2 次，多加了1次； 2．再排除—— A B A B    把多加了1次的重叠部分 A B 减去．包含与排除原理告诉我们，要计算两个集合 A B、的并集 A B 的元素的个数，可分以下两步进行：第一步：分别计算集合 A B、的元素个数，然后加起来，即先求 A B (意思是把 A B、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去 C A B   (意思是“排除”了重复计算的元素个数)．二、三量重叠问题 A 类、 B 类与 C 类元素个数的总和 A 类元素的个数 B 类元素个数 C 类元素个数  既是 A 类又是 B 类的元素个数  既是 B 类又是 C 类的元素个数  既是 A 类又是 C 类的元素个数  同时是 A 类、 B 类、 C 类的元素个数．用符号表示为： A B C A B C A B B C A C A B C   ．图示如下：             A B 图中小圆表示 A 的元素的个数，中圆表示 B 的元素的个数，大圆表示 C 的元素的个数． C A B C 1．先包含： A B C   A B C 重叠部分 A B 、B C 、C A 重叠了 2 次，多加了1次．     2．再排除： A B C A B B C A C     重叠了 3 次，但是在进行 A B C 重叠部分 A B C A B B C A C  计算时都被减掉了．               在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考． 3．再包含： A B C A B B C A C A B C   ．     7-7-1 容斥原理之重叠问题（一）.题库教师版 page 1 of 7

例题精讲两量重叠问题【例 1】小明喜欢：踢足球、上网、游泳、音乐、语文、数学；小英喜欢：数学、英语、音乐、陶艺、跳绳。用圆 A、圆 B 分别表示小明、小英的爱好，如图所示，则图中阴影部分表示________。【考点】两量重叠问题【难度】1 星【题型】填空【关键词】希望杯，四年级，二试，第 3 题【解析】阴影部分是两人都爱好的：数学、音乐【答案】数学、音乐【例 2】四（1）班全体同学站成一排，当从左向右报数时，小华报：18；当从右向左报数时，小华报：13. 那么该班有学生______________名。【考点】两量重叠问题【难度】1 星【题型】填空【关键词】希望杯，四年级，二试，第 2 题【解析】该班学生人数为：18 13 1 30 【答案】 30 名   （名）。  【例 3】实验小学四年级二班，参加语文兴趣小组的有 28 人，参加数学兴趣小组的有 29 人，有12 人两个小组都参加．这个班有多少人参加了语文或数学兴趣小组？ A C B 【考点】两量重叠问题【难度】1 星【题型】解答【解析】如图所示， A 圆表示参加语文兴趣小组的人， B 圆表示参加数学兴趣小组的人， A 与 B 重合的部分【解析】 C (阴影部分)表示同时参加两个小组的人．图中 A 圆不含阴影的部分表示只参加语文兴趣小组未参 (人)；图中 B 圆不含阴影的部分表示只参加数学兴趣小组未参加数学兴趣小组的人，有 28 12 16 (人)．加语文兴趣小组的人，有 29 12 17 方法一：由此得到参加语文或数学兴趣小组的有：16 12 17 方法二：根据包含排除法，直接可得： (人)．     45    参加语文或数学兴趣小组的人  参加语文兴趣小组的人  参加数学兴趣小组的人  两个小组都参加的人，即： 28 29 12 (人)． 45    【答案】 45 人【巩固】芳草地小学四年级有 58 人学钢琴，43 人学画画，37 人既学钢琴又学画画，问只学钢琴和只学画画的分别有多少人？ A C B 【考点】两量重叠问题【难度】1 星【题型】解答【解析】解包含与排除题，画图是一种很直观、简捷的方法，可以帮助解决问题，画图时注意把不同的对象与不同的区域对应清楚．建议教师帮助学生画图分析，清楚的分析每一部分的含义． 7-7-1 容斥原理之重叠问题（一）.题库教师版 page 2 of 7

如图， A 圆表示学画画的人， B 圆表示学钢琴的人， C 表示既学钢琴又学画画的人，图中 A 圆不含  (人)，图中 B 圆不含阴影的部分表示只学钢琴的人，阴影的部分表示只学画画的人，有： 43 37 有： 58 37 (人)． 21 6    【答案】 21 人【巩固】四(二)班有 48 名学生，在一节自习课上，写完语文作业的有 30 人，写完数学作业的有 20 人，语文数学都没写完的有 6 人． ⑴ 问语文数学都写完的有多少人？ ⑵ 只写完语文作业的有多少人？【考点】两量重叠问题【难度】1 星【题型】解答【解析】⑴ 由题意，有 48 6    (人)． 42  (人)至少完成了一科作业，根据包含排除原理，两科作业都完成的学生有：  30 20 42 8 ⑵ 只写完语文作业的人数  写完语文作业的人数-语文数学都写完的人数，即 30 8 22   (人)．【答案】 22 人【巩固】四（1）班有 46 人，其中会弹钢琴的有 30 人，会拉小提琴的有 28 人，则这个班既会弹钢琴又会拉小提琴的至少有人。【考点】两量重叠问题【难度】1 星【题型】填空【关键词】希望杯，四年级，二试，第 6 题【解析】至少一项不会的最多有(46-30)+(46-28)=34,那么两项都会的至少有 46-34=12 人【答案】12 人【例 4】如图，圆 A 表示 1 到 50 这 50 个自然数中能被 3 整除的数，圆 B 表示这 50 个数中能被 5 整除的数，则阴影部分表示的数是。【考点】两量重叠问题【难度】1 星【题型】填空【关键词】希望杯，四年级，二试，第 4 题【解析】阴影部分是 A 和 B 共有的，即 1 到 50 这 50 个自然数中能被 3×5＝15 整除的数，即 15，30，45 【答案】15 ， 30 ， 45 【例 5】学校为了丰富学生的课余生活，组建了乒乓球俱乐部和篮球俱乐部，同学们踊跃报名参加，其中有 321 人报名参加乒乓球俱乐部，429 人报名参加了篮球俱乐部，但学校最后发现有 50 人既报名参加了乒乓球俱乐部，又报名参加了篮球俱乐部，还有 23 人什么俱乐部都没报名，问该学校共有名学生．【考点】两量重叠问题【难度】1 星【题型】填空【关键词】学而思杯，4 年级，第 5 题【解析】 321 429 50 23 723  【答案】 723 人  人   【例 6】某班共有 46 人，参加美术小组的有12 人，参加音乐小组的有 23 人，有 5 人两个小组都参加了．这个班既没参加美术小组也没参加音乐小组的有多少人？【考点】两量重叠问题【难度】1 星【题型】解答【解析】已知全班总人数，从反面思考，找出参加美术或音乐小组的人数，只需用全班总人数减去这个人数，【解析】就得到既没参加美术小组也没参加音乐小组的人数．根据包含排除法知，该班至少参加了一个小组的总人数为12 23 5 30 (人)．所以，该班未参加美术或音乐小组的人数是 46 30 16 (人)．      【答案】16 人【巩固】四年级一班有 45 人，其中 26 人参加了数学竞赛，22 人参加了作文比赛，12 人两项比赛都参加了．一班有多少人两项比赛都没有参加？【考点】两量重叠问题【难度】1 星【题型】解答 7-7-1 容斥原理之重叠问题（一）.题库教师版 page 3 of 7

【解析】由包含排除法可知，至少参加一项比赛的人数是： 26 22 12 36    加的人数为： 45 36 9  (人)．  (人)，所以，两项比赛都没有参【答案】 9 人【巩固】实验二校一个歌舞表演队里，能表演独唱的有 10 人，能表演跳舞的有 18 人，两种都能表演的有 7 人．这个表演队共有多少人能登台表演歌舞？【考点】两量重叠问题【难度】1 星【题型】解答【解析】根据包含排除法，这个表演队能登台表演歌舞的人数为：10 18 7 【答案】 21 人    21 (人)．【例 7】全班 50 个学生，每人恰有三角板或直尺中的一种，28 人有直尺，有三角板的人中，男生是 14 人，若已知全班共有女生 31 人，那么有直尺的女生有____人。【考点】两量重叠问题【难度】1 星【题型】填空【关键词】华杯赛，初赛，第 8 题【解析】有三角板的学生共 50-28=22（人），其中女生 22-14=8（人），那么有直尺的女生有 31-8=23（人）。【答案】 23 人【例 8】某次英语考试由两部分组成，结果全班有12 人得满分，第一部分有 25 人做对，第二部分有19 人有错，问两部分都有错的有多少人？【考点】两量重叠问题【难度】2 星【题型】解答【解析】如图，用长方形表示参加考试的人数， A 圆表示第一部分对的人数． B 圆表示第二部分对的人数，长方形中阴影部分表示两部分都有错的人数．已知第一部分对的有 25 人，全对的有12 人，可知只对第一部分的有： 25 12 13 部分有19 人有错，其中第一部分对第二部分有错的有13 人，那么余下的19 13 6 和第二部分均有错的，两部分都有错的有 6 人．   (人)．又因为第二   (人)必是第一部分【答案】 6 人【例 9】对全班同学调查发现，会游泳的有 20 人，会打篮球的有 25 人．两项都会的有10 人，两项都不会的有 9 人．这个班一共有多少人？【考点】两量重叠问题【难度】2 星【题型】解答【解析】如图，用长方形表示全班人数， A 圆表示会游泳的人数， B 圆表示会打篮球的人数，长方形中阴影部分表示两项都不会的人数．由图中可以看出，全班人数  至少会一项的人数  两项都不会的人数，至少会一项的人数为： 20 25 10 35 (人)，全班人数为： 35 9 (人)．   44    【答案】 44 人【巩固】某班组织象棋和军棋比赛，参加象棋比赛的有 32 人，参加军棋比赛的有 28 人，有18 人两项比赛都参加了，这个班参加棋类比赛的共有多少人？ 7-7-1 容斥原理之重叠问题（一）.题库教师版 page 4 of 7

【考点】两量重叠问题【难度】2 星【题型】解答【解析】如图， A 圆表示参加象棋比赛的人， B 圆表示参加军棋比赛的人， A 与 B 重合的部分表示同时参加两项比赛的人．图中 A 圆不含阴影的部分表示只参加象棋比赛不参加军棋比赛的人，有 ( 人) ；图中 B 圆不含阴影的部分表示只参加军棋比赛不参加象棋比赛的人，有 32 18 14 (人)．由此得到参加棋类比赛的人有14 18 10 28 18 10 或者根据包含排除法直接得： 32 28 18 42  (人)． (人)．     42      【答案】 42 人【例 10】在 46 人参加的采摘活动中，只采了樱桃的有18 人，既采了樱桃又采了杏的有 7 人，既没采樱桃又没采杏的有 6 人，问：只采了杏的有多少人？【考点】两量重叠问题【难度】2 星【题型】解答【解析】如图，用长方形表示全体采摘人员 46 人， A 圆表示采了樱桃的人数， B 圆表示采了杏的人数．长方形中阴影部分表示既没采樱桃又没采杏的人数．由图中可以看出，全体人员是至少采了一种的人数与两种都没采的人数之和，则至少采了一种的人 (人)，而至少采了一种的人数  只采了樱桃的人数  两种都采了的人数  只采了杏数为： 46 6 的人数，所以，只采了杏的人数为： 40 18 7 15 (人)．     40  【答案】15 人【例 11】甲、乙、丙三个小组学雷锋，为学校擦玻璃，其中 68 块玻璃不是甲组擦的，52 块玻璃不是乙组擦的，且甲组与乙组一共擦了 60 块玻璃．那么，甲、乙、丙三个小组各擦了多少块玻璃？【考点】两量重叠问题【难度】2 星【题型】解答【解析】68 块玻璃不是甲组擦的，说明这 68 块玻璃是乙、丙两组擦的； 52 块玻璃不是乙组擦的，说明这 52 块玻璃是甲、丙两组擦的．如图，用圆 A 表示乙、丙两组擦的 68 块玻璃，B 圆表示甲、丙两组擦的 52 块玻璃．因甲乙两组共擦 (块)．丙组擦了 30 块了 60 块玻璃，那么 68 52 60 60 玻璃．乙组擦了： 68 30 38  (块)玻璃，甲组擦了： 52 30 (块)，这是两个丙组擦的玻璃数．60 2 30   (块)玻璃．   22   (块)玻璃，乙组擦了： 68 30 38     22 【答案】甲组擦了： 52 30   (块)玻璃，丙组擦了 30 块玻璃。【例 12】育才小学画展上展出了许多幅画，其中有 16 幅画不是六年级的，有 15 幅画不是五年级的，五、六年级共展出 25 幅画，其他年级的画共有多少幅？【考点】两量重叠问题【难度】2 星【题型】解答【解析】通过 16 幅画不是六年级的可以知道，五年级和其他年级的画作数量之和是 16，通过 15 幅画不是五年级的可以知道六年级和其他年级的画作数量之和是 15，那也就是说五年级的画比六年级多 1 幅，我们还知道五、六年级共展出 25 幅画，进而可以求出五年级画作有 13 幅，六年级画作有 12 幅，那么久可以求出其他年级的画作共有 3 幅．【答案】 3幅【例 13】 47 名学生参加数学和语文考试，其中语文得分 95 分以上的14 人，数学得分 95 分以上的 21 人，两 7-7-1 容斥原理之重叠问题（一）.题库 page 5 of 7 教师版

门都不在 95 分以上的有 22 人．问：两门都在 95 分以上的有多少人？【考点】两量重叠问题【难度】2 星【题型】解答【解析】如图，用长方形表示这 47 名学生， A 圆表示语文得分 95 分以上的人数， B 圆表示数学得 95 分以上【解析】的人数， A 与 B 重合的部分表示两门都在 95 分以上的人数，长方形内两圆外的部分表示两门都不在 95 分以上的人数．由图中可以看出，全体人数是至少一门在 95 分以上的人数与两门都不在 95 分以上的人数之和，则至 (人)．根据包含排除法，两门都在 95 分以上的人数为：少一门在 95 分以上的人数为： 47 22 14 21 25 10 (人)． 25      【答案】10 人【巩固】有100 位旅客，其中有10 人既不懂英语又不懂俄语，有 75 人懂英语， 83 人懂俄语．问既懂英语又懂俄语的有多少人？【考点】两量重叠问题【难度】2 星【题型】解答【关键词】迎春杯【解析】方法一：在100 人中懂英语或俄语的有：100 10 90     (人)．从 83 位懂俄语的旅客中除去只懂俄语的人，剩下的83 15 有：90 75 15 英语又懂俄语的旅客．方法二：学会把公式进行适当的变换，由包含与排除原理，得： (人)．又因为有 75 人懂英语，所以只懂俄语的 (人)就是既懂 68 A B A B A B       75 83 90    68 (人)．【答案】 68 人【例 14】一个班 48 人，完成作业的情况有三种：一种是完成语文作业没完成数学作业；一种是完成数学作业没完成语文作业；一种是语文、数学作业都完成了．已知做完语文作业的有 37 人；做完数学作业的有 42 人．这些人中语文、数学作业都完成的有多少人？【考点】两量重叠问题【难度】2 星【题型】解答【解析】不妨用下图来表示：【解析】完成语文作业的人数 A D C B 完成数学作业的人数线段 AB 表示全班人数，线段 AC 表示做完语文作业的人数，线段 DB 表示做完数学作业的人数，重叠部分 DC 则表示语文、数学都做完的人数．根据题意，做完语文作业的有 37 人，即 AC  ．做完数学作业的有 42 人，即 DB  ． 37 42 AC DB 48 AB  DC  ①式减②式，就有  (人) 37 42 79   (人)  ①  ② 79 48 31   (人),所以，数学、语文作业都做完的有 31人．【答案】 31人【巩固】四年级科技活动组共有 63 人．在一次剪贴汽车模型和装配飞机模型的定时科技活动比赛中，老师到时清点发现：剪贴好一辆汽车模型的同学有 42 人，装配好一架飞机模型的同学有 34 人．每个同学都至少完成了一项活动．问：同时完成这两项活动的同学有多少人？【考点】两量重叠问题【难度】2 星【题型】解答【解析】因 42 34 76  ，76  根据包含排除法知， 42 34 数) 63 ．由减法运算法则知，完成两项活动的人数为 76 63 13   63 ，所以必有人同时完成了这两项活动．由于每个同学都至少完成了一项活动，  (完成了两项活动的人数)  全组人数，即 76  (完成了两项活动的人 (人)．也可画图分析．【答案】13 人 7-7-1 容斥原理之重叠问题（一）.题库教师版 page 6 of 7

【巩固】科技活动小组有 55 人．在一次制作飞机模型和制作舰艇模型的定时科技活动比赛中，老师到时清点发现：制作好一架飞机模型的同学有 40 人，制作好一艘舰艇的同学有 32 人．每个同学都至少完成了一项制作．问两项制作都完成的同学有多少人？【考点】两量重叠问题【难度】2 星【题型】解答 A C B 【解析】因为 40 32 72   ， 72 55 ，所以必有人两项制作都完成了．由于每个同学都至少完成了一项制作，  完成了两项制作的  完成了两项制作的人数，即 55 72  根据包含排除法可知：全组人数 40 32 人数．所以，完成了两项制作的人数为： 72 55 17    (人)．【答案】17 人【例 15】一次数学测验，甲答错题目总数的 1 4 ，乙答错 3 道题，两人都答错的题目是题目总数的 1 6 ．求甲、乙都答对的题目数. 【考点】两量重叠问题【难度】3 星【题型】解答【解析】(法一)设共有 n 道题．由右图知 d 即为所求，并有关系式 (1) n 4 3(2) 由①③知,n 是 4 和 6 的公倍数，    a c   c b     n   c 6  (3) b   ，由于 b 是非负整数，所以 n=12，由此求出 c=2，b=1，即 12 的倍数．将③代入②，有 3 a=1.又由 a+b+c+d=n，得到 d=n-（a+b+c)=8（法二）显然两人都答错的题目不多于 3 道，所以题目总数只可能是 6、12、18，其中只有 12，能使甲答错题目总数是整数. n 6 【答案】 8 道题【例 16】小赵、小钱、小孙、小李、小周、小吴、小郑、小王，这 8 名同学站成一排．其中小孙和小周不能相邻，小钱和小吴也不能相邻，小李必须在小郑和小王之间(可相邻也可不相邻)．则不同的排列方法共有________种．【考点】两量重叠问题【难度】3 星【题型】填空【解析】8 名同学站成一排，所有的排法共有 8! 40320   种，小钱和小吴相邻的也有10080 种，这两对都相邻的有 2 2 6! 2880 种，其中小孙和小周相邻的排法，根据“捆绑法”有 2 7! 10080  种．根据容斥原理，符合前两个条件的排法有 40320 2 10080 2880 种．在这 23040 种排法里面，小李、小郑、小王 3 个人的排列中每个人在中间的可能性都相等，所以小李在小郑和小王之间的排法占其中的 1 3 23040 23040 ，即有 7680       种． 1 3    【答案】 7680 种 7-7-1 容斥原理之重叠问题（一）.题库教师版 page 7 of 7

分享到：

赞收藏

资料库

7-7-1 容斥原理之重叠问题（一）.学生版.doc

相关推荐

小学奥数

热门标签

最新资料