7-2-1 简单乘法原理.学生版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：0.51M 资料格式：doc 举报版权申诉

第1页 / 共8页

第2页 / 共8页

第3页 / 共8页

第4页 / 共8页

第5页 / 共8页

第6页 / 共8页

第7页 / 共8页

第8页 / 共8页

文本预览

7-2-1.简单乘法原理教学目标 1.使学生掌握乘法原理主要内容，掌握乘法原理运用的方法； 2.使学生分清楚什么时候用乘法原理，分清有几个必要的步骤，以及各步之间的关系． 3.培养学生准确分解步骤的解题能力；乘法原理的数学思想主旨在于分步考虑问题，本讲的目的也是为了培养学生分步考虑问题的习惯．知识要点一、乘法原理概念引入老师周六要去给同学们上课，首先得从家出发到长宁上 8 点的课，然后得赶到黄埔去上下午 1 点半的课．如果说申老师的家到长宁有 5 种可选择的交通工具（公交、地铁、出租车、自行车、步行），然后再从长宁到黄埔有 2 种可选择的交通工具（公交、地铁），同学们，你们说老师从家到黄埔一共有多少条路线？我们看上面这个示意图，老师必须先的到长宁，然后再到黄埔．这几个环节是必不可少的，老师是一定要先到长宁上完课，才能去黄埔的．在没学乘法原理之前，我们可以通过一条一条的数，把线路找出来，显而易见一共是 10 条路线．但是要是老师从家到长宁有 25 种可选择的交通工具，并且从长宁到黄埔也有 30 种可选择的交通工具，那一共有多少条线路呢？这样数，恐怕是要耗费很多的时间了．这个时候我们的乘法原理就派上上用场了．二、乘法原理的定义完成一件事，这个事情可以分成 n 个必不可少的步骤（比如说老师从家到黄埔，必须要先到长宁，那么一共可以分成两个必不可少的步骤，一是从家到长宁，二是从长宁到黄埔），第 1 步有 A 种不同的方法，第二步有 B 种不同的方法，……，第 n 步有 N 种不同的方法．那么完成这件事情一共有 A×B×……×N 种不同的方法．结合上个例子，老师要完成从家到黄埔的这么一件事，需要 2 个步骤，第 1 步是从家到长宁，一共 5 种选择；第 2 步从长宁到黄埔，一共 2 种选择；那么老师从家到黄埔一共有 5×2 个可选择的路线了，即 10 条．三、乘法原理解题三部曲 1、完成一件事分 N 个必要步骤； 2、每步找种数（每步的情况都不能单独完成该件事）； 3、步步相乘四、乘法原理的考题类型 1、路线种类问题——比如说老师举的这个例子就是个路线种类问题； 2、字的染色问题——比如说要 3 个字，然后有 5 种颜色可以给每个字然后，问 3 个字有多少种染色方法； 3、地图的染色问题——同学们可以回家看地图，比如中国每个省的染色情况，给你几种颜色，问你一张 7-2-1.简单乘法原理.题库教师版 page 1 of 8

包括几个部分的地图有几种染色的方法； 4、排队问题——比如说 6 个同学，排成一个队伍，有多少种排法； 5、数码问题——就是对一些数字的排列，比如说给你几个数字，然后排个几为数的偶数，有多少种排法．例题精讲【例 1】邮递员投递邮件由 A 村去 B 村的道路有 3 条，由 B 村去 C 村的道路有 2 条，那么邮递员从 A 村经 B 村去 C 村，共有多少种不同的走法？北 A 中南 B 【考点】简单乘法原理【解析】把可能出现的情况全部考虑进去．【难度】1 星 1 号路 C 号路 2 【题型】解答第一步第二步南北中 A 村 A 村 A 村 B 村 B 村 B 村 1 2 1 2 1 2 号路号路号路号路号路号路 C 村 C 村 C 村由分析知邮递员由 A 村去 B 村是第一步，再由 B 村去 C 村为第二步，完成第一步有 3 种方法，而每种方法的第二步又有 2 种方法．根据乘法原理，从 A 村经 B 村去 C 村，共有 3×2=6 种方法．【答案】 6 【巩固】如下图所示，从 A 地去 B 地有 5 种走法，从 B 地去 C 地有 3 种走法，那么李明从 A 地经 B 地去 C 地有多少种不同的走法？ C B A 【考点】简单乘法原理【解析】从 A 地经 B 地去 C 地分为两步，由 A 地去 B 地是第一步，再由 B 地去 C 地为第二步，完成第一步有 5 种方法，而每种方法的第二步又有 3 种方法．根据乘法原理，从 A 地经 B 地去 C 地，共有 5×3=15 种方法．【题型】解答【难度】1 星【答案】15 【例 2】如下图中，小虎要从家沿着线段走到学校，要求任何地点不得重复经过．问：他最多有几种不同走法？学校家【考点】简单乘法原理【解析】从家到中间结点一共有 2 种走法，从中间结点到学校一共有 3 种走法，根据乘法原理，一共有 3×2=6 【题型】解答【难度】1 星种走法．【答案】6 【巩固】在下图中，一只甲虫要从 A 点沿着线段爬到 B 点，要求任何点不得重复经过．问：这只甲虫最多有几种不同走法？ 7-2-1.简单乘法原理.题库教师版 page 2 of 8

A C 【考点】简单乘法原理【解析】甲虫要从 A 点沿着线段爬到 B 点，需要经过两步，第一步是从 A 点到 C 点，一共有 3 种走法；第二【难度】1 星步是从 C 点到 B 点，一共也有 3 种走法，根据乘法原理一共有 3×3=9 种走法． B 【题型】解答【答案】9 【巩固】在右图中，一只甲虫要从 A 点沿着线段爬到 B 点，要求任何点不得重复经过．问：这只甲虫最多有几种不同走法？ A B C D 【考点】简单乘法原理【解析】从 A 点沿着线段爬到 B 点需要分成三步进行，第一步，从 A 点到 C 点，一共有 3 种走法；第二步，从 C 点到 D 点，有 1 种走法；第三步，从 D 点到 B 点，一共也有 3 种走法．根据乘法原理，一共有 3×1×3=9 种走法．【题型】解答【难度】2 星【答案】9 【巩固】在右图中，一只蚂蚁要从 A 点沿着线段爬到 B 点，要求任何点不得重复经过．问：这只蚂蚁最多有几种不同走法？ A B C D 【难度】2 星【考点】简单乘法原理【解析】解这道题时千万不要受铺垫题目的影响，第一步，A 点到 C 点的走法是 3 种；第二步，从 C 点到 D 点，有 1 种走法；但第三步，从 D 点到 B 点的走法并不是 3 种，由 D 出去有 2 条路选择，到下一岔路口又有 2 条路选择，所总共有 2×2=4（种）走法，根据乘法原理，这只蚂蚁最多有 3 1 4 12    （种）不同走法．【题型】解答【答案】12 【巩固】在右图中，一只甲虫要从 A 点沿着线段爬到 B 点，要求任何点不得重复经过．问：这只甲虫最多有几种不同走法？ A B C D 【考点】简单乘法原理【解析】从 A 点沿着线段爬到 B 点需要分成三步进行，第一步，从 A 点到 C 点，一共有 3 种走法；第二步，从 C 点到 D 点，一共也有 3 种走法；第三步，从 D 点到 B 点，一共也有 3 种走法．根据乘法原理，一共有 3 3 3 27    种走法．【题型】解答【难度】2 星【答案】 27 【巩固】在右图中，一只甲虫要从 A 点沿着线段爬到 B 点，要求任何点不得重复经过．问：这只甲虫最多有几种不同走法? 7-2-1.简单乘法原理.题库教师版 page 3 of 8

B C 【考点】简单乘法原理【解析】解这道题时千万不要受铺垫题目的影响， A 点到 C 点的走法不是 3 种，而是 4 种， C 点到 B 点的走【题型】解答法也是 4 种，根据乘法原理，这只甲虫最多有 4 4 16   种走法． A 【难度】3 星【答案】16 【例 3】如果将四面颜色不同的小旗子挂在一根绳子上，组成一个信号，那么这四面小旗子可组成种不同的信号。【考点】简单乘法原理【难度】1 星【题型】填空【关键词】希望杯，4 年级，1 试【解析】4×3×2×1=24 【答案】 24 种【巩固】按下表给出的词造句，每句必须包括一个人、一个交通工具，以及一个目的地，请问可以造出多少个不同的句子？【考点】简单乘法原理【解析】1、造一个句子必须包含三个部分，即人、交通工具、目的地．【题型】解答【难度】2 星 2、那么这个句子可以分成三个部分；第一个步——选择人物，有三种选择；第二步——选择交通工具，有三种选择；第三个步——选择目的地，有三种选择． 3、根据乘法原理：3×3×3=27．【答案】27 【巩固】小琴、小惠、小梅三人报名参加运动会的跳绳，跳高和短跑这三个项目的比赛，每人参加一项，报名的情况有______ 种。【考点】简单乘法原理【难度】3 星【题型】填空【关键词】希望杯，4 年级，1 试【解析】乘法原理，3×3×3=27 种【巩固】题库中有三种类型的题目，数量分别为 30 道、40 道和 45 道，每次考试要从三种类型的题目中各取一道组成一张试卷．问：由该题库共可组成多少种不同的试卷？【题型】解答【难度】2 星【考点】简单乘法原理【解析】从该题库每一类试卷中分三步各选一道题，每一步分别有 30、40、45 种选法．根据乘法原理，一共有 30×40×45=54000 种不同的选法，所以一共可以组成 54000 种不同试卷．【答案】54000 【巩固】文艺活动小组有 3 名男生，4 名女生，从男、女生中各选 1 人做领唱，有多少种选法？【考点】简单乘法原理【解析】完成这件事需要两步：一步是从女生中选 1 人，有 4 种选法；另一步是从男生中选 1 人，有 3 种选法．因此，由乘法原理，选出 1 男 1 女的方法有 3 4 12   种．还可以用乘法的意义来理解这道题：男生有 3 种选法，每选定 1 个男生，再选 1 个女生，对应着 4 种选法，即 3 个男生，每个男生对应 4 种选女生的方法，因此选出 1 男 1 女共有 3 4 12   种方法．【难度】2 星【题型】解答【答案】12 【巩固】要从四年级六个班中评选出学习、体育、卫生先进集体，有多少种不同的评选结果？【考点】简单乘法原理【题型】解答【难度】2 星 7-2-1.简单乘法原理.题库教师版 page 4 of 8

【解析】第一步选出学习先进集体一共有 6 种方法，第二步选出体育先进集体一共有 6 种方法，第三步选出卫生先进集体一共有 6 种评选方法，根据乘法原理，一共有 6 6 6    种评选方法． 216 【答案】 216 【例 4】小丸子有许多套服装，帽子的数量为 5 顶、上衣有 10 件，裤子有 8 条，还有皮鞋 6 双，每次出行要从几种服装中各取一个搭配．问：共可组成多少种不同的搭配(帽子可以选择戴与不戴)？【难度】2 星【考点】简单乘法原理【解析】小丸子搭配服装分四步．第一步选帽子，由于不戴帽子可以看作戴了顶空帽子，所以有 5 1 6   种选法；第二步选上衣，有 10 种选法；第三步选裤子，有 8 种选法；第四步选皮鞋，有 6 种选法．根据种选法，所以一共可以组成 2880 乘法原理，四种服装中各取一个搭配．一共有 5 1 10 8 6 种不同搭配．【题型】解答   （）    2880 【答案】2880 【例 5】已知图 3 是一个轴对称图形，若将图中某些黑色的图形去掉后，得到一些新的图形，则其中轴对称图形共有（）个。（A）9 （B）8 （C）7 （D）6 【考点】简单乘法原理【难度】3 星【题型】选择【关键词】华杯赛，初赛，第 4 题【解析】两个眼睛可以去掉也可以不去掉有 2 种选择，同理嘴和脚也是各有两种选择，所以共有 2 2 2=8   种选择，但是题目说的新图型，所以要去掉题目已给的形式，共有 8 1=7  种，所以答案是：C 【答案】 C 【例 6】从四年级六个班中评选出学习、体育、卫生先进集体，如果要求同一个班级只能得到一个先进集体，那么一共有多少种评选方法？【考点】简单乘法原理【解析】第一步选出学习先进集体共有 6 种方法，第二步从剩下班级中选出体育先进集体共有 5 种方法，第【题型】解答【难度】2 星三步选出卫生先进集体只剩有 4 种评选方法，根据乘法原理，共有 6×5×4=120 种评选方法．【答案】120 【巩固】奥运吉祥物中的 5 个“福娃”取“北京欢迎您”的谐音：贝贝、京京、欢欢、迎迎、妮妮。如果在盒子中从左向右放 5 个不同的“福娃”，那么，有________种不同的放法。【考点】简单乘法原理【难度】2 星【题型】填空【关键词】希望杯，五年级，二试，第 2 题【解析】 5 个“福娃”各不相同，所以放第一个时有 5 种放法，放第二个时有 4 种放法，放第三个时有 3 种放法，放第四个时有 2 种放法，放第五个时有1种放法，总共有： 5 4 3 2 1 120      种放法。【答案】120 种【例 7】从全班 20 人中选出 3 名学生排队，一共有多少种排法？【考点】简单乘法原理【解析】分三步，分别挑选第一人，第二人，第三人，分别有 20，19，18 种挑选法，一共有 20 19 18 6840 【难度】2 星【题型】解答    种排法．【答案】 6840 【例 8】五位同学扮成奥运会吉祥物福娃贝贝、晶晶、欢欢、迎迎和妮妮，排成一排表演节目．如果贝贝 7-2-1.简单乘法原理.题库教师版 page 5 of 8

和妮妮不相邻，共有多少种不同的排法？【考点】简单乘法原理【解析】五位同学的排列方式共有 5×4×3×2×1=120（种）．【难度】3 星【题型】解答如果将相邻的贝贝和妮妮看作一人，那么四人的排列方式共有 4×3×2×1=24（种）；因为贝贝和妮妮可以交换位置，所以贝贝和妮妮相邻的排列方式有 24×2=48(种)；贝贝和妮妮不相邻的排列方式有 120-48=72（种）．【答案】72 【巩固】 10 个人围成一圈，从中选出三个人，其中恰有两人相邻，共有多少种不同选法？【考点】简单乘法原理【解析】两人相邻的情况有 10 种，第三个人不能与他们相邻，所以对于每一种来说，只剩 6 个人可选，10×6=60 【难度】3 星【题型】解答（种）共有 60 种不同的选法．【答案】 60 种【巩固】 12 个人围成一圈，从中选出 3 个人，其中恰有两个人相邻，共有种不同的选法。【考点】简单乘法原理【难度】星【题型】填空【关键词】学而思杯，6 年级，第 4 题【解析】现在恰有两个人相邻，我们首先来从这 12 个人中选出两个相邻的人，由于这 12 个人是围成 1 圈的，那么共有 12 种选法；根据乘法原理，共有 12×8=96 种【答案】 96 种【例 9】 “数学”这个词的英文单词是“MATH”．用红、黄、蓝、绿、紫五种颜色去分别给字母染色，每个字母染的颜色都不一样．这些颜色一共可以染出多少种不同搭配方式？【考点】简单乘法原理【解析】为了完成对单词“MATH”的染色，我们可以按字母次序，把这个染色过程分四步依次完成：【题型】解答【难度】2 星第 1 步——对字母“M”染色，此时有 5 种颜色可以选择；第 2 步——对字母“A”染色，由于字母“M”已经用过一种颜色，所以对字母“A”染色只有 4 种颜色可以选择；第 3 步——对字母“T”染色，由于字母“M”和“A”已经用去了 2 种颜色，所以对字母“T”染色只剩 3 种颜色可以选择；第 4 步——对字母“H”，染色，由于字母“M”、“A”和“T”已经用去了 3 种颜色，所以对字母“H”染色只有 2 种颜色可以选择．由乘法原理，共可以得到 5 4 3 2 120     种不同的染色方式．【小结】下面的这棵枚举树清晰地揭示了利用乘法原理分步计数的过程： M A T H M 有种选择，这是其中的一种染法 5 红每种选择有种搭配 4 黄蓝绿紫每种搭配又可搭配种 3 蓝绿紫每种搭配又可搭配种 2 绿紫思考一下，如果不要求“每个字母染的颜色都不一样”，会有多少种不同的染色方式？每个字母都有５种颜色可选，那么染色方式一共有 5×5×5×5=625 种染色方式．【答案】120 【巩固】 “IMO”是国际数学奥林匹克的缩写，把这 3 个字母用 3 种不同颜色来写，现有 5 种不同颜色的笔，问共有多少种不同的写法？【考点】简单乘法原理【解析】第一步写“I”有 5 种方法，第二步写“M”有 4 种方法，第三步写“O”有 3 种方法，共有 5 4 3 60 【题型】解答    种【难度】2 星方法．【答案】 60 7-2-1.简单乘法原理.题库教师版 page 6 of 8

【巩固】 “学习改变命运”这六个字要用 6 种不同颜色来写，现只有 6 种不同颜色的笔，问共有多少种不同的写法？【考点】简单乘法原理【解析】第一步写“学”有 6 种方法，第二步写“习”有 5 种方法，第三步写“改”有 4 种方法，第四步写“变”有 3 种方法，第五步写 “ 命 ” 有 2 种方法，第六步写 “ 运 ” 有 1 种方法，根据乘法原理，一共有 6 5 4 3 2 1 720       种方法．【题型】解答【难度】2 星【答案】 720 【例 10】有 6 种不同颜色的笔，来写“学习改变命运”这六个字，要求相邻字的颜色不能相同，有多少种不同的方法？【考点】简单乘法原理【解析】写第一个字有 6 种选择，以后每写一个字，只要保证不与前一个字相同就行了，都有 5 种选择，所【难度】2 星【题型】解答以，有 6 5 5 5 5 5 18750       种写法．【答案】18750 【巩固】用 5 种不同颜色的笔来写“智康教育”这几个字，相邻的字颜色不同，共有多少种写法？【考点】简单乘法原理【解析】第一个字有 5 种写法，第二个字有 4 种写法，第三个字也是 4 种写法，同理后面的字也是 4 种写法，【难度】2 星【题型】解答共有 5×4×4×4=320 种．【答案】320 【例 11】联欢会上有一则数字谜语，谜底是一个八位数。现已猜出：□54□7□39，主持人提示：“这个无重复数字的八位数中，最小的数是 2。”要猜出这个谜语，最多还要猜次。【考点】简单乘法原理【难度】2 星【题型】填空【关键词】希望杯，六年级，一试，第 12 题【解析】根据题意三个方框只能从 2，6，8 中选，根据乘法原理最多还要猜 3 2 1 6 【答案】 6 次    次【例 12】在右面每个方格中各放 1 枚围棋子(黑子或白子)，有（）种放法．【考点】简单乘法原理【难度】2 星【题型】填空【关键词】走美四年级初赛第 5 题【解析】每个方格中有 2 种填法：故 2×2×2×2=16（种）【答案】16 种【例 13】将 1～6 分别填入图中的 6 个方框内，使得同一行中左边的数比右边的小，同一列中上边的数比下边的小，共有______种不同的填法．【考点】简单乘法原理【关键词】走美杯，3 年级，初赛，第 12 题【解析】根据题意可知 1 和 6 的位置是固定只能添在左上角和右下角如图所示：【难度】2 星【题型】填空将余下的 4 个格编号如图根据同一行中左边的数比右边的小，同一列中上边的数比下边的小的原则知道 2 只能选择（1）或者（2）号位置，当 2 的位置确定后 3 的位值也就确定了，故当 2 选择（1）时 3 只能选择（2），当 2 选择（2）时 3 只能选择（1），共有 2 种填法，同理 4 和 5 只能在（3）和 7-2-1.简单乘法原理.题库教师版 page 7 of 8

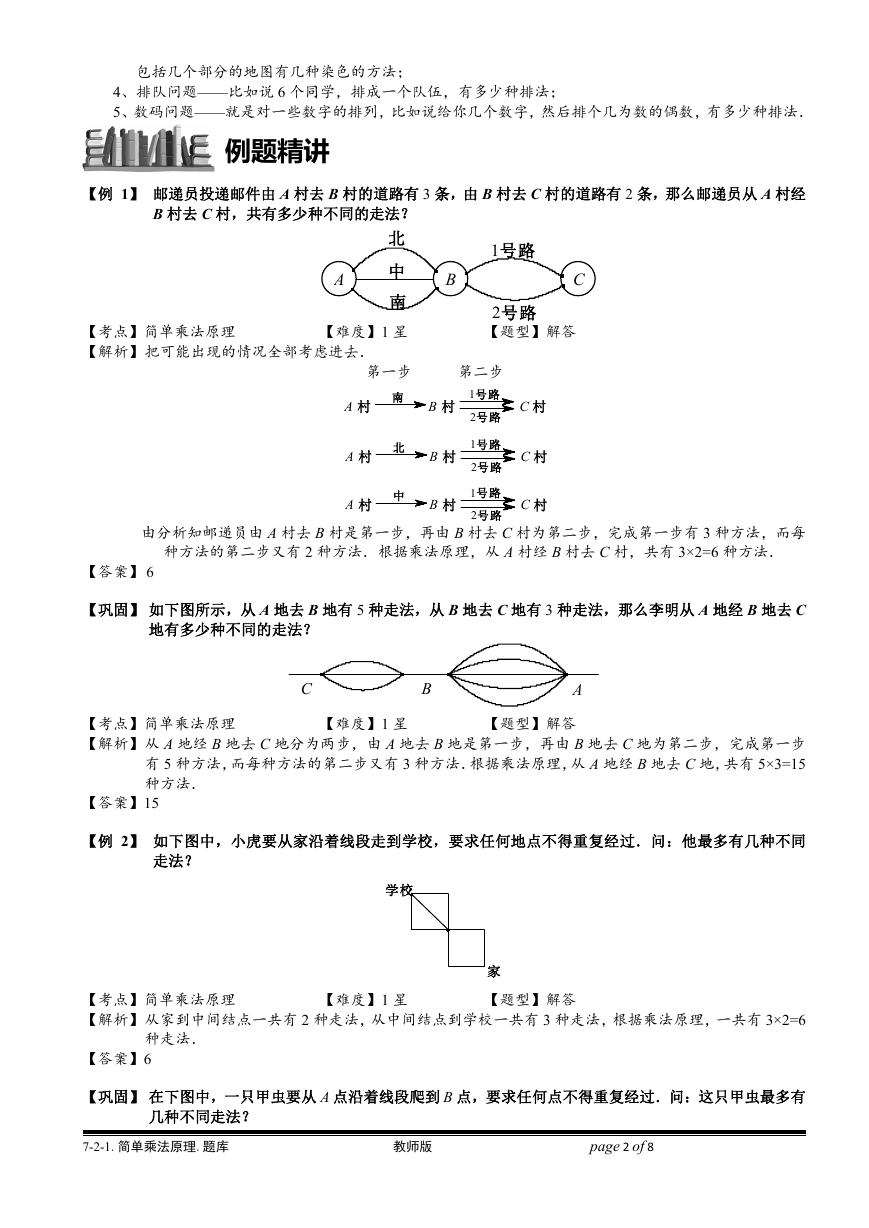
（4）中互选，根据乘法原理，所以本题一共有 2 2   （种）不同填法。 4 【答案】 4 种【例 14】将 19 枚棋子放入 5 5 的方格网内，每个方格至多只放一枚棋子，且每行每列的棋子个数均为奇数个，那么共有________种不同的放法．【考点】简单乘法原理【难度】3 星【题型】填空【关键词】迎春杯，高年级，初试，7 题【解析】反过来考虑 6 个空格，则肯定是某 3 行和某 3 列中每行每列各有 2 个，如下：【解析】 □表示空格，○表示有棋子的方格，其他方格全部有棋子．选择有空格的 3 行 3 列有10 10 100 选法，在这 3 行 3 列中选择哪 6 个格空有 3 2 1 6    种选法，所以总共有 600 种．  种  【答案】 600 种 7-2-1.简单乘法原理.题库教师版 page 8 of 8

分享到：

赞收藏

资料库

7-2-1 简单乘法原理.学生版.doc

相关推荐

小学奥数

热门标签

最新资料