4-4-2 圆与扇形（二）.教师版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：2.56M 资料格式：doc 举报版权申诉

第1页 / 共26页

第2页 / 共26页

第3页 / 共26页

第4页 / 共26页

第5页 / 共26页

第6页 / 共26页

第7页 / 共26页

第8页 / 共26页

文本预览

圆与扇形例题精讲研究圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形，通过变动图形的位置或对图形进行分割、旋转、拼补，使它变成可以计算出面积的规则图形来计算它们的面积．圆的面积 2πr ；扇形的面积 2π r  圆的周长 2πr  ；扇形的弧长 2π  r n 360 n  360 ；．一、跟曲线有关的图形元素： ①扇形：扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形，扇形是圆的一部分．我们经常说的 1 2 圆等等其实都是扇形，而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几圆、 1 4 圆、 1 6 比如：扇形的面积  所在圆的面积分之几．那么一般的求法是什么呢？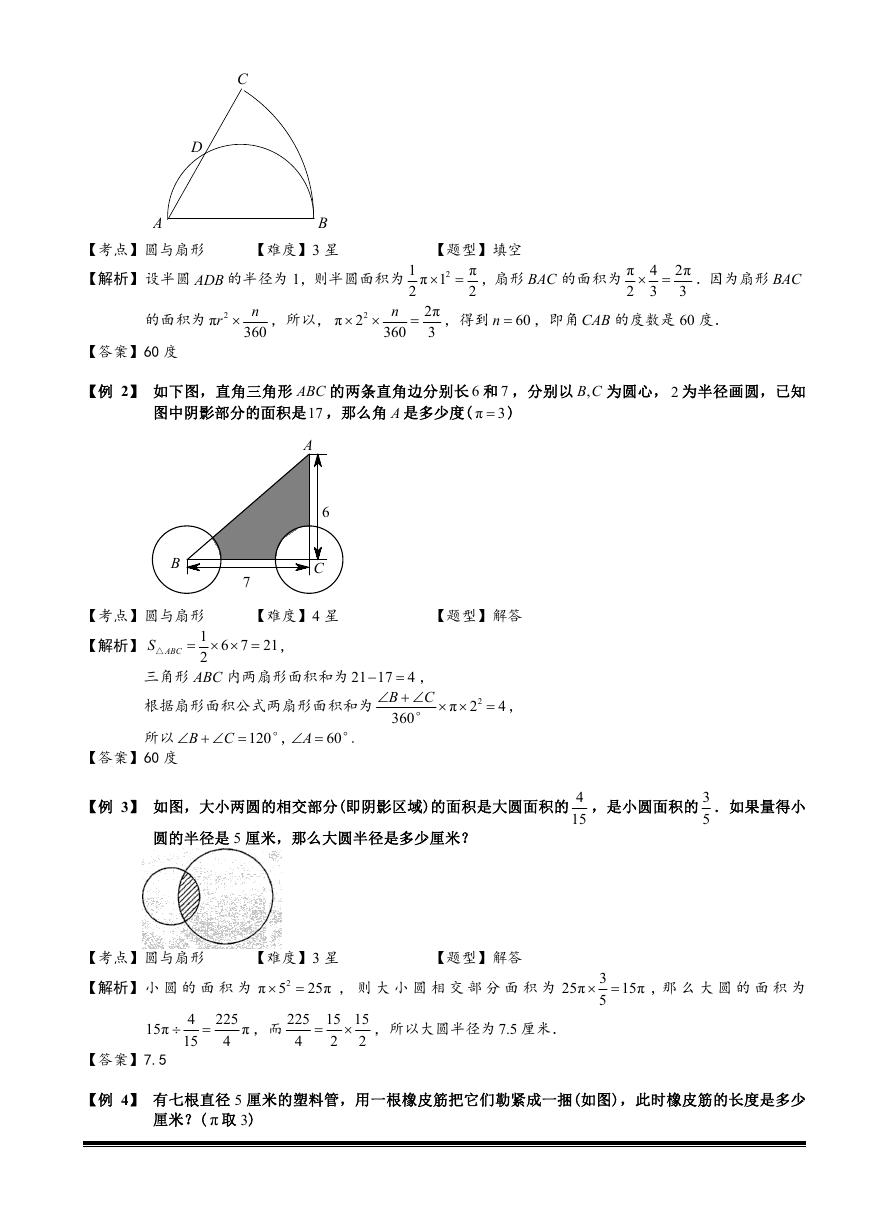关键是 n ； 360 n 360 扇形中的弧长部分  所在圆的周长 n ． 360 n 360 扇形的周长  所在圆的周长  2 半径(易错点是把扇形的周长等同于扇形的弧长) ②弓形：弓形一般不要求周长，主要求面积．一般来说，弓形面积  扇形面积-三角形面积．(除了半圆) ③”弯角”：如图：弯角的面积  正方形-扇形 ④”谷子”：如图： “谷子”的面积  弓形面积 2 二、常用的思想方法： ①转化思想(复杂转化为简单，不熟悉的转化为熟悉的) ②等积变形(割补、平移、旋转等) ③借来还去(加减法) ④外围入手(从会求的图形或者能求的图形入手，看与要求的部分之间的”关系”) 板块二曲线型面积计算【例 1】如图，已知扇形 BAC 的面积是半圆 ADB 面积的 4 倍，则角 CAB 的度数是________． 3

C D A B 【考点】圆与扇形【难度】3 星【解析】设半圆 ADB 的半径为 1，则半圆面积为的面积为 2π r  ，所以， n 360 π 2  2  n 360 【题型】填空  ，扇形 BAC 的面积为 π π 2 2 2 π 1  1 2  ，得到 60 n  ，即角 CAB 的度数是 60 度．   ．因为扇形 BAC 4 3 2π 3 2π 3 【答案】60 度【例 2】如下图，直角三角形 ABC 的两条直角边分别长 6 和 7 ，分别以 ,B C 为圆心， 2 为半径画圆，已知图中阴影部分的面积是17 ，那么角 A 是多少度( π 3 ) A 6 C B 7 【考点】圆与扇形【解析】 S △ ABC 1 6 7 21     2 , 【难度】4 星【题型】解答三角形 ABC 内两扇形面积和为 21 17 4  ， B C    360 ° 根据扇形面积公式两扇形面积和为      °, 120 C B A  °. 60 π 2   2  4 , 所以【答案】60 度【例 3】如图，大小两圆的相交部分(即阴影区域)的面积是大圆面积的 4 15 圆的半径是 5 厘米，那么大圆半径是多少厘米？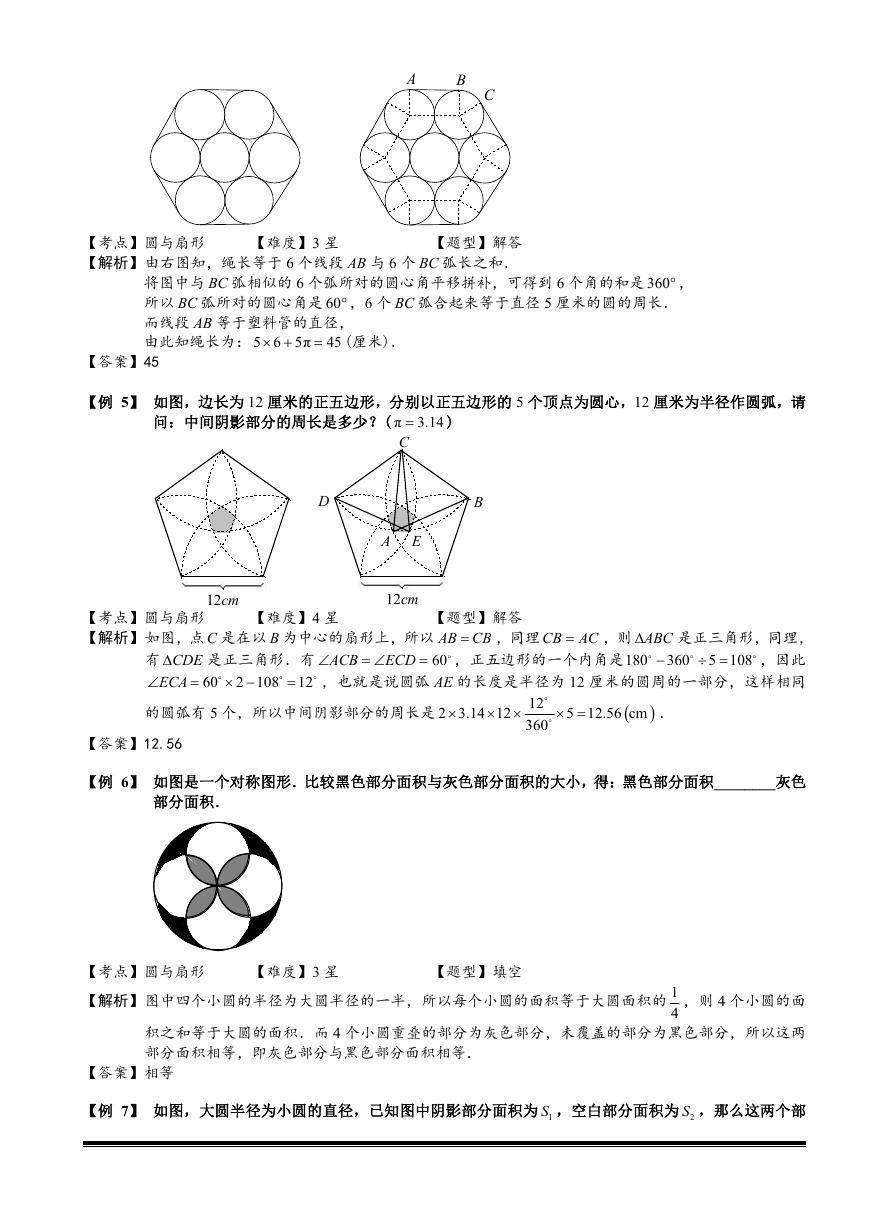，是小圆面积的 3 5 ．如果量得小【考点】圆与扇形【题型】解答【解析】小圆的面积为，则大小圆相交部分面积为 25π   3 5 15π , 那么大圆的面积为  ，所以大圆半径为 7.5 厘米． 2 【难度】3 星 π 5 25π   ，而 225 4  15 15 2 2 15π  4 15  225 4 π 【答案】7.5 【例 4】有七根直径 5 厘米的塑料管，用一根橡皮筋把它们勒紧成一捆(如图)，此时橡皮筋的长度是多少厘米？( π 取 3)

A B C 【考点】圆与扇形【题型】解答【解析】由右图知，绳长等于 6 个线段 AB 与 6 个 BC 弧长之和．【难度】3 星将图中与 BC 弧相似的 6 个弧所对的圆心角平移拼补，可得到 6 个角的和是 360 ，所以 BC 弧所对的圆心角是 60 ，6 个 BC 弧合起来等于直径 5 厘米的圆的周长．而线段 AB 等于塑料管的直径，由此知绳长为： 5 6 5π (厘米)．   45  【答案】45 【例 5】如图，边长为 12 厘米的正五边形，分别以正五边形的 5 个顶点为圆心，12 厘米为半径作圆弧，请问：中间阴影部分的周长是多少？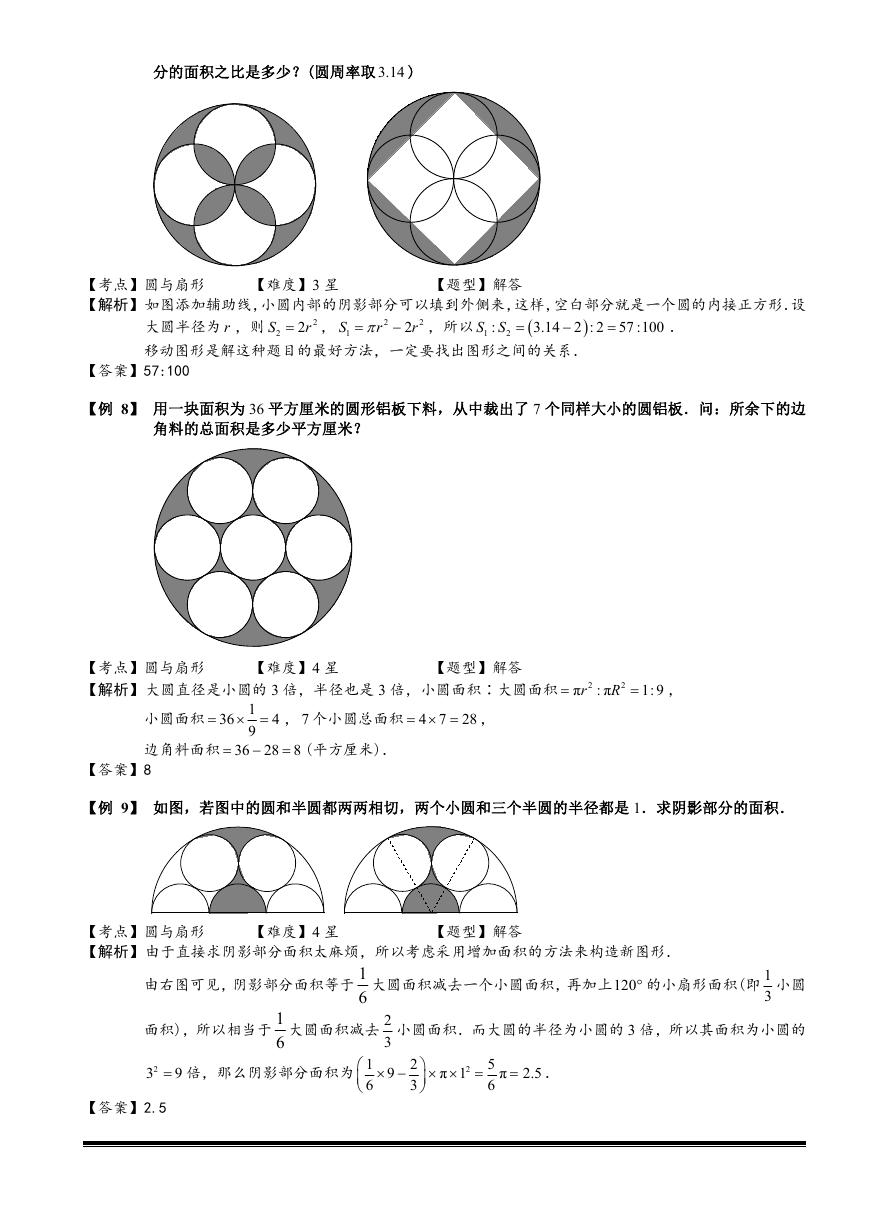( π  C 3.14 ) D B A E 12 cm 12 cm 【难度】4 星【考点】圆与扇形【解析】如图，点 C 是在以 B 为中心的扇形上，所以 AB CB ，同理 CB AC ，则 ABC  是正三角形，同理，  ，因此   ，也就是说圆弧 AE 的长度是半径为 12 厘米的圆周的一部分，这样相同  ，正五边形的一个内角是180 【题型】解答 5 108 ACB   360 60     是正三角形．有 60 12 有 CDE ECA  的圆弧有 5 个，所以中间阴影部分的周长是 2 108  ECD       2 3.14 12    12  360    5 12.56 cm   ．【答案】12.56 【例 6】如图是一个对称图形．比较黑色部分面积与灰色部分面积的大小，得：黑色部分面积________灰色部分面积．【考点】圆与扇形【解析】图中四个小圆的半径为大圆半径的一半，所以每个小圆的面积等于大圆面积的 1 4 【题型】填空【难度】3 星，则 4 个小圆的面积之和等于大圆的面积．而 4 个小圆重叠的部分为灰色部分，未覆盖的部分为黑色部分，所以这两部分面积相等，即灰色部分与黑色部分面积相等．【答案】相等【例 7】如图，大圆半径为小圆的直径，已知图中阴影部分面积为 1S ，空白部分面积为 2S ，那么这两个部

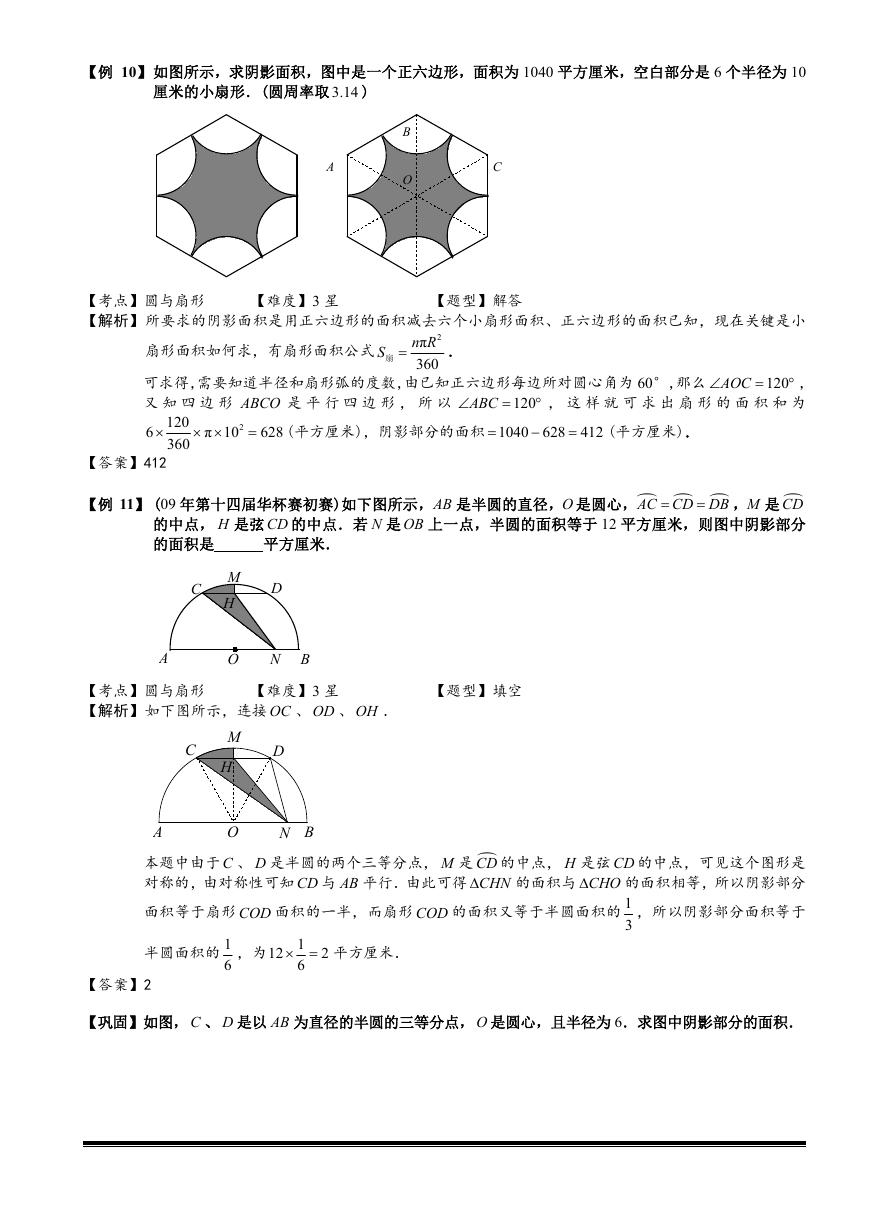
分的面积之比是多少？(圆周率取 3.14 ) 【考点】圆与扇形【解析】如图添加辅助线，小圆内部的阴影部分可以填到外侧来，这样，空白部分就是一个圆的内接正方形．设【题型】解答【难度】3 星  大圆半径为 r ，则移动图形是解这种题目的最好方法，一定要找出图形之间的关系．  ，所以 S S  1 r ， r  2 r S 1 2 S  : 2 2 2 2 3.14 2 : 2 57 :100   ． 2 【答案】57:100 【例 8】用一块面积为 36 平方厘米的圆形铝板下料，从中裁出了 7 个同样大小的圆铝板．问：所余下的边角料的总面积是多少平方厘米？【考点】圆与扇形【解析】大圆直径是小圆的 3 倍，半径也是 3 倍，小圆面积∶大圆面积 2 r 【题型】解答【难度】4 星 π  2 : π R  ， 1:9 小圆面积  36   ， 7 个小圆总面积 4 7    ， 28 4 边角料面积 36 28 8  (平方厘米)．  1 9  【答案】8 【例 9】如图，若图中的圆和半圆都两两相切，两个小圆和三个半圆的半径都是 1．求阴影部分的面积．【考点】圆与扇形【解析】由于直接求阴影部分面积太麻烦，所以考虑采用增加面积的方法来构造新图形．【题型】解答【难度】4 星由右图可见，阴影部分面积等于 1 6 大圆面积减去一个小圆面积，再加上120 的小扇形面积(即 1 3 小圆面积)，所以相当于 1 6 大圆面积减去 2 3 小圆面积．而大圆的半径为小圆的 3 倍，所以其面积为小圆的 23 9 倍，那么阴影部分面积为【答案】2.5    1 6   9 2 3    2 π 1    5 6 π  2.5 ．

【例 10】如图所示，求阴影面积，图中是一个正六边形，面积为 1040 平方厘米，空白部分是 6 个半径为 10 厘米的小扇形．(圆周率取 3.14 ) A B O C 【考点】圆与扇形【解析】所要求的阴影面积是用正六边形的面积减去六个小扇形面积、正六边形的面积已知，现在关键是小【题型】解答【难度】3 星扇形面积如何求，有扇形面积公式 S 扇 2π n R 360 ．可求得，需要知道半径和扇形弧的度数，由已知正六边形每边所对圆心角为 60°，那么又知四边形 ABCO 是平行四边形，所以 6 (平方厘米)，阴影部分的面积 1040 628 412  ，  ，这样就可求出扇形的面积和为 ABC  (平方厘米)． 120  AOC 628   π 10 120     2  120 360 【答案】412 【例 11】 (09 年第十四届华杯赛初赛)如下图所示，AB 是半圆的直径，O 是圆心，   AC CD DB  ，M 是 CD 的中点， H 是弦 CD 的中点．若 N 是 OB 上一点，半圆的面积等于 12 平方厘米，则图中阴影部分的面积是平方厘米．  C M H D A O N B 【考点】圆与扇形【解析】如下图所示，连接 OC 、 OD 、 OH ．【难度】3 星【题型】填空 C M H D B N O A 本题中由于 C 、 D 是半圆的两个三等分点， M 是 CD 的中点， H 是弦 CD 的中点，可见这个图形是对称的，由对称性可知 CD 与 AB 平行．由此可得 CHN 的面积与 CHO 的面积相等，所以阴影部分面积等于扇形 COD 面积的一半，而扇形 COD 的面积又等于半圆面积的 1 3 半圆面积的 1 6 ，为 1 6 ，所以阴影部分面积等于   平方厘米． 12  2 【答案】2 【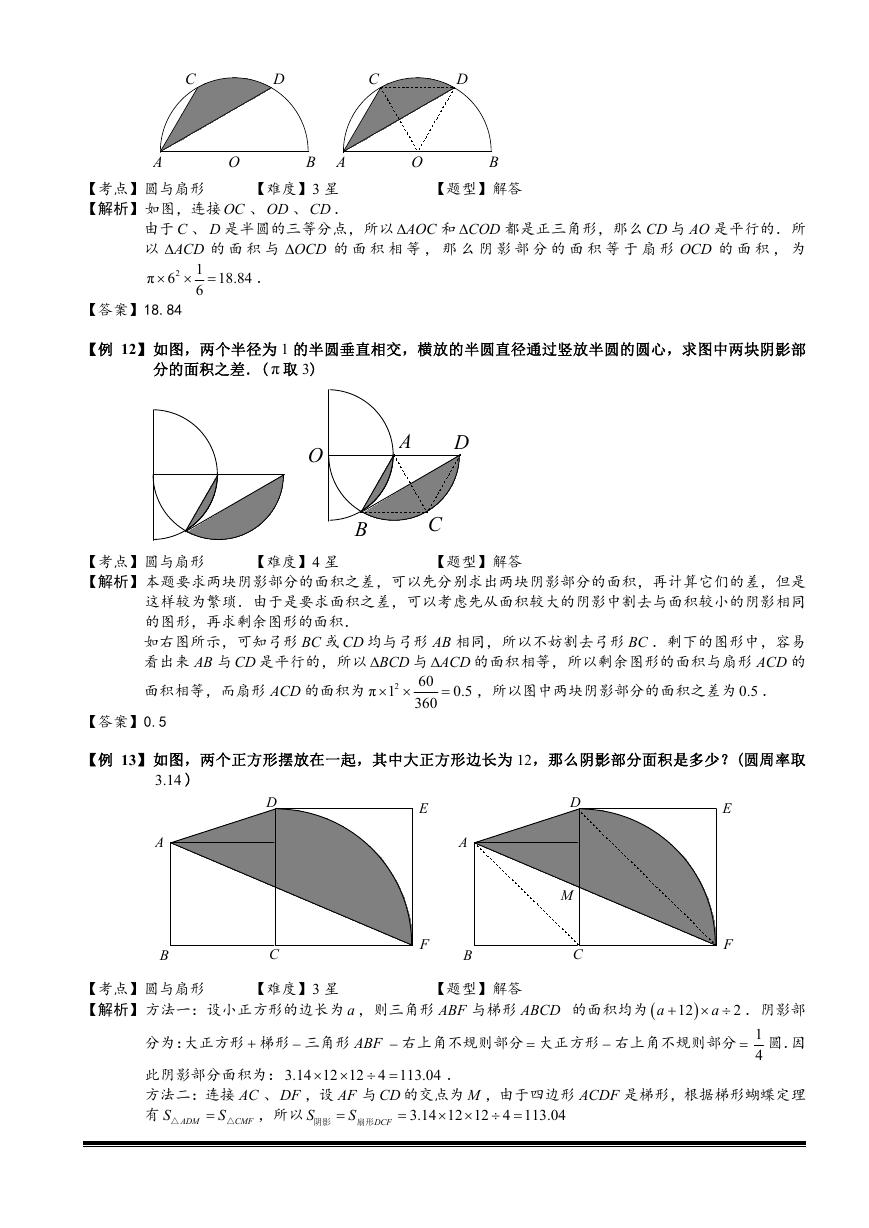巩固】如图， C 、 D 是以 AB 为直径的半圆的三等分点， O 是圆心，且半径为 6．求图中阴影部分的面积．

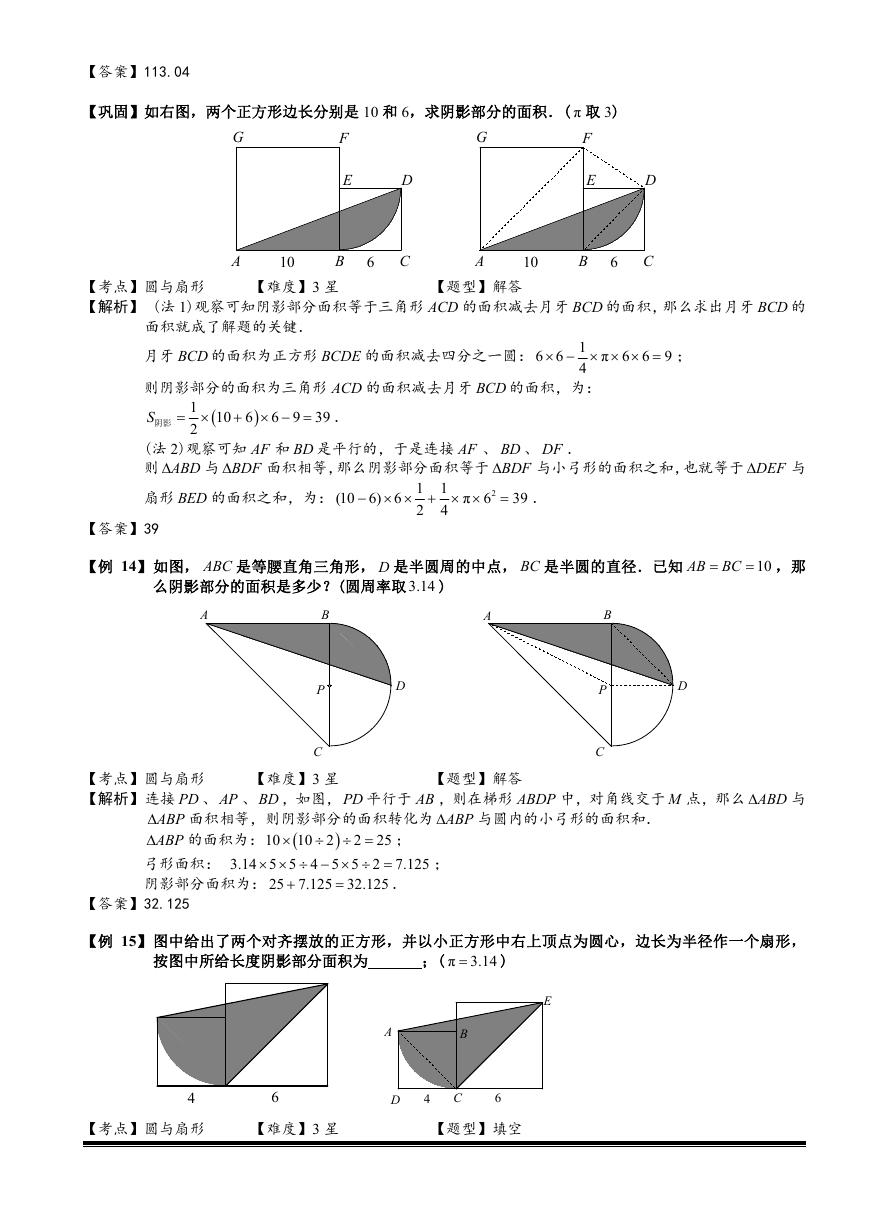
C D C D A A 【难度】3 星【考点】圆与扇形【解析】如图，连接 OC 、 OD 、 CD ． O B O B 【题型】解答由于 C 、 D 是半圆的三等分点，所以 AOC 以 ACD 1 π 6  6 的面积与 OCD 18.84   ． 2 都是正三角形，那么 CD 与 AO 是平行的．所的面积相等，那么阴影部分的面积等于扇形 OCD 的面积，为和 COD 【答案】18.84 【例 12】如图，两个半径为 1 的半圆垂直相交，横放的半圆直径通过竖放半圆的圆心，求图中两块阴影部分的面积之差．( π 取 3) O A D B C 【难度】4 星【题型】解答【考点】圆与扇形【解析】本题要求两块阴影部分的面积之差，可以先分别求出两块阴影部分的面积，再计算它们的差，但是这样较为繁琐．由于是要求面积之差，可以考虑先从面积较大的阴影中割去与面积较小的阴影相同的图形，再求剩余图形的面积．如右图所示，可知弓形 BC 或 CD 均与弓形 AB 相同，所以不妨割去弓形 BC ．剩下的图形中，容易看出来 AB 与 CD 是平行的，所以 BCD 的面积相等，所以剩余图形的面积与扇形 ACD 的面积相等，而扇形 ACD 的面积为 2 π 1    ，所以图中两块阴影部分的面积之差为 0.5 ．与 ACD 60 0.5 360 【答案】0.5 【例 13】如图，两个正方形摆放在一起，其中大正方形边长为 12，那么阴影部分面积是多少？(圆周率取 3.14 ) D C A B E F A B D M C E F 【考点】圆与扇形【解析】方法一：设小正方形的边长为 a ，则三角形 ABF 与梯形 ABCD 的面积均为 【题型】解答【难度】3 星 a  12   ．阴影部 a 2 分为：大正方形  梯形  三角形 ABF  右上角不规则部分  大正方形  右上角不规则部分  1 4 此阴影部分面积为： 3.14 12 12 4 113.04 方法二：连接 AC 、DF ，设 AF 与 CD 的交点为 M ，由于四边形 ACDF 是梯形，根据梯形蝴蝶定理有 ADM 3.14 12 12 4 113.04 △ ，所以 CMF S S阴影圆．因     S ．     S △ 扇形 DCF 

【答案】113.04 【巩固】如右图，两个正方形边长分别是 10 和 6，求阴影部分的面积．( π 取 3) F E D G F E D G A 【考点】圆与扇形【解析】 (法 1)观察可知阴影部分面积等于三角形 ACD 的面积减去月牙 BCD 的面积，那么求出月牙 BCD 的【题型】解答 10 B 【难度】3 星 6 C A 10 B 6 C 面积就成了解题的关键．月牙 BCD 的面积为正方形 BCDE 的面积减去四分之一圆： 6 6       ； π 6 6 9 1 4 则阴影部分的面积为三角形 ACD 的面积减去月牙 BCD 的面积，为： S 6 9 39     10 6   ．  阴影  1 2 (法 2)观察可知 AF 和 BD 是平行的，于是连接 AF 、 BD 、 DF ．则 ABD 扇形 BED 的面积之和，为：面积相等，那么阴影部分面积等于 BDF 39      (10 6) 6 与 BDF  ． π 6    2 1 2 1 4 与小弓形的面积之和，也就等于 DEF  与【答案】39 【例 14】如图， ABC 是等腰直角三角形， D 是半圆周的中点， BC 是半圆的直径．已知么阴影部分的面积是多少？(圆周率取 3.14 ) AB BC  ，那 10 A A D B P C B P C D 【考点】圆与扇形【解析】连接 PD 、 AP 、BD ，如图，PD 平行于 AB ，则在梯形 ABDP 中，对角线交于 M 点，那么 ABD 【题型】解答【难度】3 星与与圆内的小弓形的面积和．面积相等，则阴影部分的面积转化为 ABP 的面积为：   ABP 25 10 ABP 弓形面积： 3.14 5 5 4 5 5 2 7.125        阴影部分面积为： 25 7.125 32.125   ； 10 2 ；． 2     【答案】32.125 【例 15】图中给出了两个对齐摆放的正方形，并以小正方形中右上顶点为圆心，边长为半径作一个扇形，按图中所给长度阴影部分面积为；( π 3.14  ) E A B 4 6 D 4 C 6 【考点】圆与扇形【难度】3 星【题型】填空

【解析】连接小正方形 AC ,有图可见 ABC △ 扇形  S S  1 4 4    2 S 阴影  ∵ S  1 1 2 2 ∴ 2 AC  同理 2 △ ACD 2 AC 32  48 ACD AC CE 72 CE  ，∴ 1 48 24    2 90 π 4  360 24 12.56 8 28.56   12.56   ，   S 2 △ ∴ S △ S 扇形 ∴ S 1 4 4 8     2 ABC 阴影【答案】28.56 【例 16】如图，图形中的曲线是用半径长度的比为 2 :1.5: 0.5 的 6 条半圆曲线连成的．问：涂有阴影的部分的面积与未涂有阴影的部分的面积的比是多少？【考点】圆与扇形【解析】假设最小圆的半径为 r ，则三种半圆曲线的半径分别为 4r ， 3r 和 r ．【题型】解答【难度】4 星 1 阴影部分的面积为：  π 4 r 2 空白部分的面积为：  2 π 4 则阴影部分面积与空白部分面积的比为 5 :11． 1 2 5π r 1 2 ，  π 3 r 11π r π r     r   2 2 2 2 2  2 π r  2 5π r ，【答案】5:11 【例 17】(西城实验考题)奥运会的会徽是五环图，一个五环图是由内圆直径为 6 厘米，外圆直径为 8 厘米的五个环组成，其中两两相交的小曲边四边形(阴影部分)的面积都相等，已知五个圆环盖住的面积是 77.1 平方厘米，求每个小曲边四边形的面积．( π 3.14  ) 【考点】圆与扇形【解析】⑴每个圆环的面积为：【难度】4 星 2 π 4  2 π 3 7π   ⑵五个圆环的面积和为： 21.98 5 109.9   ⑶八个阴影的面积为：109.9 77.1 32.8  ⑷每个阴影的面积为： 32.8 8 4.1 (平方厘米)．  (平方厘米)； (平方厘米)；     【题型】解答 21.98 (平方厘米)；【答案】4.1 【例 18】已知正方形 ABCD 的边长为 10 厘米，过它的四个顶点作一个大圆，过它的各边中点作一个小圆， ) 再将对边中点用直线连擎起来得右图．那么，图中阴影部分的总面积等于______方厘米．( π 3.14 

分享到：

赞收藏

资料库

4-4-2 圆与扇形（二）.教师版.doc

相关推荐

小学奥数

热门标签

最新资料