4-3-1 三角形等高模型与鸟头模型（一）.教师版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：4.29M 资料格式：doc 举报版权申诉

第1页 / 共37页

4-3-1 三角形等高模型与鸟头模型（一）.教师版.doc.pdf-第2页.jpg

第2页 / 共37页

4-3-1 三角形等高模型与鸟头模型（一）.教师版.doc.pdf-第3页.jpg

第3页 / 共37页

4-3-1 三角形等高模型与鸟头模型（一）.教师版.doc.pdf-第4页.jpg

第4页 / 共37页

4-3-1 三角形等高模型与鸟头模型（一）.教师版.doc.pdf-第5页.jpg

第5页 / 共37页

4-3-1 三角形等高模型与鸟头模型（一）.教师版.doc.pdf-第6页.jpg

第6页 / 共37页

4-3-1 三角形等高模型与鸟头模型（一）.教师版.doc.pdf-第7页.jpg

第7页 / 共37页

4-3-1 三角形等高模型与鸟头模型（一）.教师版.doc.pdf-第8页.jpg

第8页 / 共37页

文本预览

4-3-1.三角形等高模型与鸟头模型例题精讲板块一三角形等高模型我们已经知道三角形面积的计算公式：三角形面积  底 高 2 从这个公式我们可以发现：三角形面积的大小，取决于三角形底和高的乘积．如果三角形的底不变，高越大(小)，三角形面积也就越大(小)；如果三角形的高不变，底越大(小)，三角形面积也就越大(小)；这说明当三角形的面积变化时，它的底和高之中至少有一个要发生变化．但是，当三角形的底和高同时发生变化时，三角形的面积不一定变化．比如当高变为原来的 3 倍，底变为原来的 1 3 样．这就是说：一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化．同时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状．，则三角形面积与原来的一在实际问题的研究中，我们还会常常用到以下结论： ①等底等高的两个三角形面积相等； ②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；如左图 1 : S S : a b  2 S ③夹在一组平行线之间的等积变形，如右上图 ACD 反之，如果 ACD ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)； ⑤三角形面积等于与它等底等高的平行四边形面积的一半； ⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比． △ ，则可知直线 AB 平行于CD ． △ ； BCD S BCD △ S △ S 【例 1】你有多少种方法将任意一个三角形分成：⑴ 3 个面积相等的三角形；⑵ 4 个面积相等的三角形； ⑶6 个面积相等的三角形．【考点】三角形的等高模型【难度】1 星【题型】解答【解析】⑴ 如下图，D、E 是 BC 的三等分点，F、G 分别是对应线段的中点，答案不唯一： ⑵ 如下图，答案不唯一，以下仅供参考： 4-3-1.三角形等高模型与鸟头模型题库 page 1 of 37

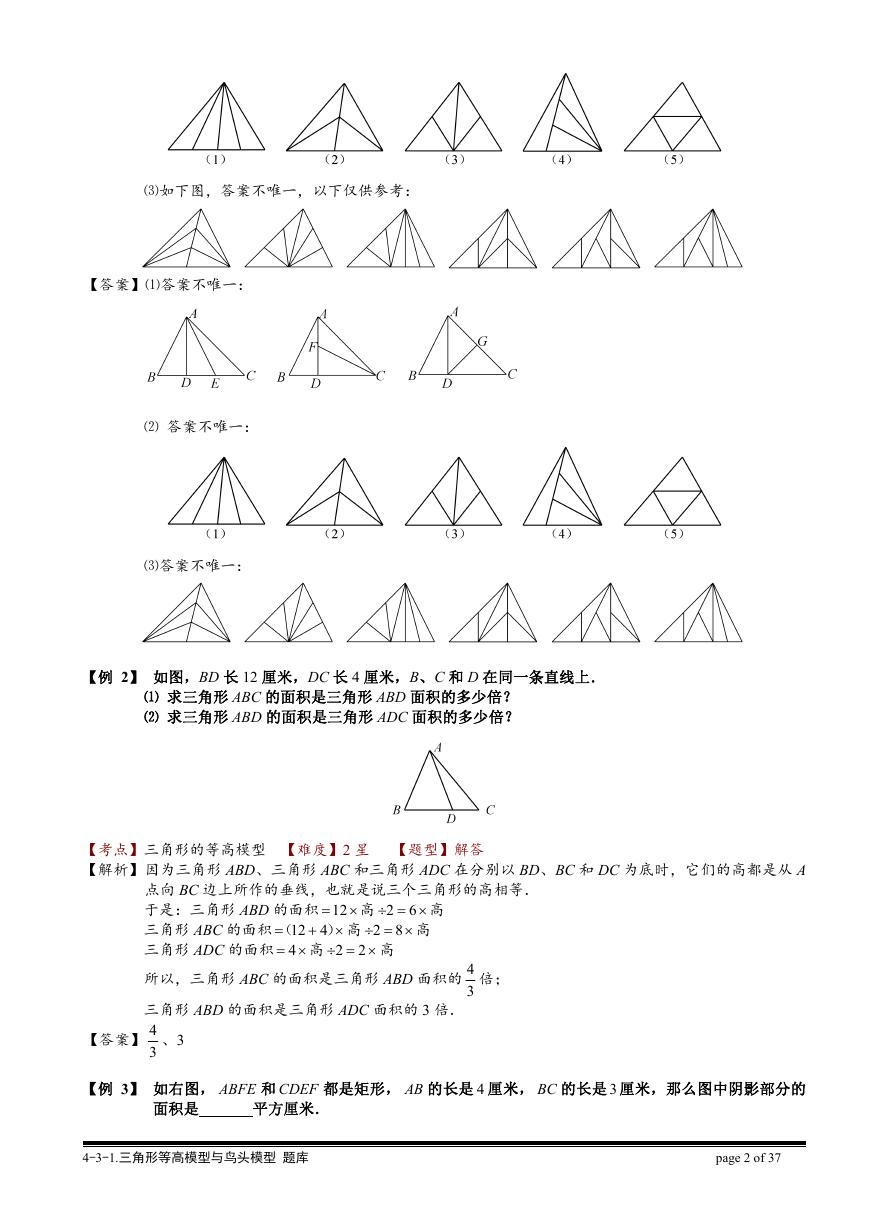
⑶如下图，答案不唯一，以下仅供参考：【答案】⑴答案不唯一： ⑵ 答案不唯一： ⑶答案不唯一：【例 2】如图，BD 长 12 厘米，DC 长 4 厘米，B、C 和 D 在同一条直线上． ⑴ 求三角形 ABC 的面积是三角形 ABD 面积的多少倍？ ⑵ 求三角形 ABD 的面积是三角形 ADC 面积的多少倍？【考点】三角形的等高模型【难度】2 星【题型】解答【解析】因为三角形 ABD、三角形 ABC 和三角形 ADC 在分别以 BD、BC 和 DC 为底时，它们的高都是从 A  高 2 6    高点向 BC 边上所作的垂线，也就是说三个三角形的高相等．于是：三角形 ABD 的面积 12 三角形 ABC 的面积 12 4 ）高 2 8  三角形 ADC 的面积 4  高 2    高所以，三角形 ABC 的面积是三角形 ABD 面积的 4 3 三角形 ABD 的面积是三角形 ADC 面积的 3 倍．    高 2 倍；  （  【答案】 4 3 、3 【例 3】如右图， ABFE 和 CDEF 都是矩形， AB 的长是 4 厘米， BC 的长是 3 厘米，那么图中阴影部分的面积是平方厘米． 4-3-1.三角形等高模型与鸟头模型题库 page 2 of 37

【考点】三角形的等高模型【难度】2 星【题型】解答【解析】图中阴影部分的面积等于长方形 ABCD 面积的一半，即 4 3 2 6 【答案】6    (平方厘米)．【巩固】(2009 年四中小升初入学测试题)如图所示，平行四边形的面积是 50 平方厘米，则阴影部分的面积是平方厘米．【考点】三角形的等高模型【难度】2 星【题型】解答【解析】根据面积比例模型，可知图中空白三角形面积等于平行四边形面积的一半，所以阴影部分的面积也等于平行四边形面积的一半，为 50 2   平方厘米． 25 【答案】25 【巩固】如下图，长方形 AFEB 和长方形 FDCE 拼成了长方形 ABCD ，长方形 ABCD 的长是 20，宽是 12，则它内部阴影部分的面积是．【考点】三角形的等高模型【难度】2 星【题型】解答【解析】根据面积比例模型可知阴影部分面积等于长方形面积的一半，为 1 20 12 120 【答案】120 2    ．【例 4】如图，长方形 ABCD 的面积是 56 平方厘米，点 E 、F 、G 分别是长方形 ABCD 边上的中点，H 为 AD 边上的任意一点，求阴影部分的面积． A E B H D G C F A E B H D G C F 【考点】三角形的等高模型【难度】2 星【题型】解答【解析】本题是等底等高的两个三角形面积相等的应用． S 连接 BH 、 CH ． ∵ AE EB ， S ∴ AEH S 同理， BFH S △ ． BEH S ∴ S 长方形阴影 △ △ ABCD 1 2 【答案】28 △ ，S CFH  CGH =S 1 56   2   ， DGH (平方厘米)． 28 4-3-1.三角形等高模型与鸟头模型题库 page 3 of 37

【巩固】图中的 E 、F 、G 分别是正方形 ABCD 三条边的三等分点，如果正方形的边长是12 ，那么阴影部分的面积是． A E B F D G C 6 5 A E B F H 1 2 4 3 D G C 【考点】三角形的等高模型【难度】2 星【题型】解答【解析】把另外三个三等分点标出之后，正方形的 3 个边就都被分成了相等的三段．把 H 和这些分点以及正方形的顶点相连，把整个正方形分割成了 9 个形状各不相同的三角形．这 9 个三角形的底边分别是在正方形的 3 个边上，它们的长度都是正方形边长的三分之一．阴影部分被分割成了 3 个三角形，右边三角形的面积和第1第 2 个三角形相等：中间三角形的面积和第 3 第 4 个三角形相等；左边三角形的面积和第 5 个第 6 个三角形相等．因此这 3 个阴影三角形的面积分别是 ABH 、BCH 和 CDH 的三分之一，因此全部阴影的总面积就等于正方形面积的三分之一．正方形的面积是144 ，阴影部分的面积就是 48 ．【答案】48 【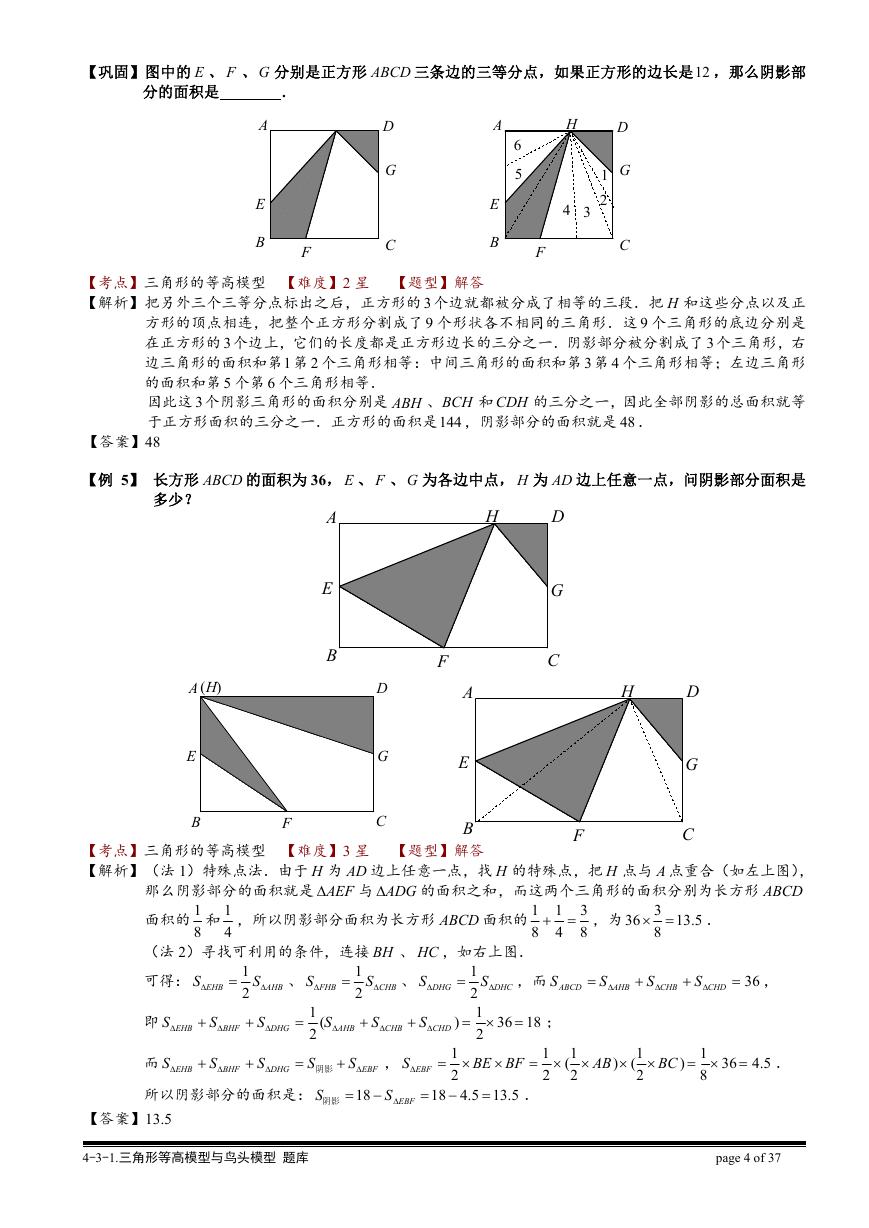例 5】长方形 ABCD 的面积为 36， E 、 F 、G 为各边中点， H 为 AD 边上任意一点，问阴影部分面积是多少？ A ( ) H E A E B H D G C F A E D G H D G B F B 【考点】三角形的等高模型【难度】3 星【题型】解答【解析】（法 1）特殊点法．由于 H 为 AD 边上任意一点，找 H 的特殊点，把 H 点与 A 点重合（如左上图）， C F 那么阴影部分的面积就是 AEF 与 ADG 的面积之和，而这两个三角形的面积分别为长方形 ABCD C 和 1 8 面积的 1 8 （法 2）寻找可利用的条件，连接 BH 、 HC ，如右上图．，所以阴影部分面积为长方形 ABCD 面积的 1 4 1 4 3 8   ，为 36   13.5 ． 3 8 S 、  AHB S  S 、 S  DHG  CHB  ，而 S ABCD  S AHB   S CHB   S CHD   ， 36 可得： S  EHB  即 S  EHB  S  BHF 1 2  S  DHG AHB S  CHB  S  36 18  ； FHB ( S  1 2 S 阴影    1 2  S  EBF 18   S DHC 1 2 1   2 BE BF  ) CHD 1 2  S EBF  18 4.5 13.5  而 EHB  S  S  BHF  S  DHG ， S  EBF   所以阴影部分的面积是： S 阴影  【答案】13.5 4-3-1.三角形等高模型与鸟头模型题库   1 2 ( 1 2  AB )  ( 1 2  BC )   1 8 36  ． 4.5 ． page 4 of 37

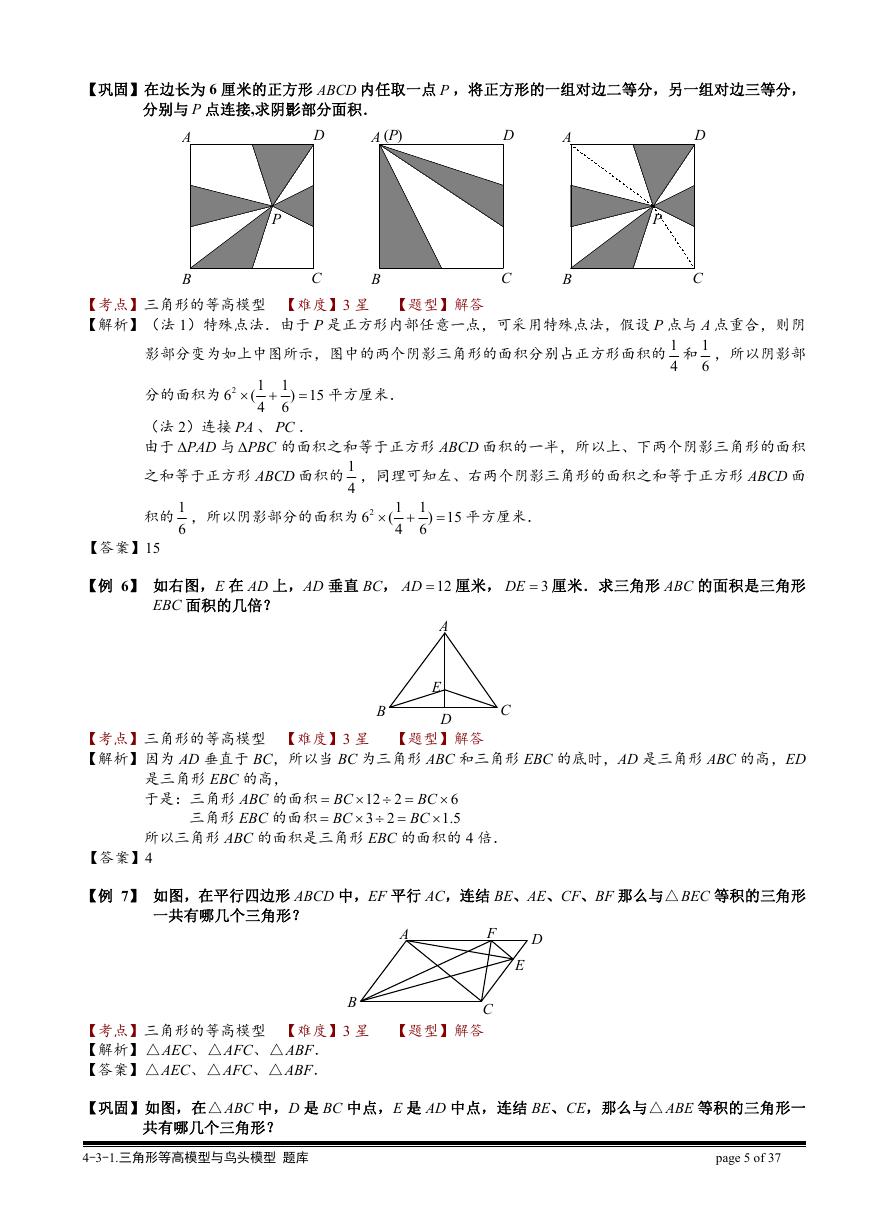
【巩固】在边长为 6 厘米的正方形 ABCD 内任取一点 P ，将正方形的一组对边二等分，另一组对边三等分，分别与 P 点连接,求阴影部分面积． A D A ( ) P D A P B C B C B 【考点】三角形的等高模型【难度】3 星【题型】解答【解析】（法 1）特殊点法．由于 P 是正方形内部任意一点，可采用特殊点法，假设 P 点与 A 点重合，则阴影部分变为如上中图所示，图中的两个阴影三角形的面积分别占正方形面积的 1 4 和 1 6 ，所以阴影部 D C P 分的面积为 2 6  (  ) 15  平方厘米． 1 4 1 6 与 PBC （法 2）连接 PA 、 PC ．由于 PAD 之和等于正方形 ABCD 面积的 1 4 积的 1 6 ，所以阴影部分的面积为 2 6 【答案】15  ( 1 4  1 6 ) 15  平方厘米．的面积之和等于正方形 ABCD 面积的一半，所以上、下两个阴影三角形的面积，同理可知左、右两个阴影三角形的面积之和等于正方形 ABCD 面【例 6】如右图，E 在 AD 上，AD 垂直 BC， EBC 面积的几倍？ AD  厘米， 12 DE  厘米．求三角形 ABC 的面积是三角形 3 A E 【考点】三角形的等高模型【难度】3 星【题型】解答【解析】因为 AD 垂直于 BC，所以当 BC 为三角形 ABC 和三角形 EBC 的底时，AD 是三角形 ABC 的高，ED B D C 是三角形 EBC 的高，于是：三角形 ABC 的面积三角形 EBC 的面积   BC BC 12 2    3 2    6 BC  1.5 BC  所以三角形 ABC 的面积是三角形 EBC 的面积的 4 倍．【答案】4 【例 7】如图，在平行四边形 ABCD 中，EF 平行 AC，连结 BE、AE、CF、BF 那么与△BEC 等积的三角形一共有哪几个三角形？ A F D E C 【考点】三角形的等高模型【难度】3 星【题型】解答【解析】 △AEC、△AFC、△ABF．【答案】△AEC、△AFC、△ABF． B 【巩固】如图，在△ABC 中，D 是 BC 中点，E 是 AD 中点，连结 BE、CE，那么与△ABE 等积的三角形一共有哪几个三角形？ 4-3-1.三角形等高模型与鸟头模型题库 page 5 of 37

A E D C B 【考点】三角形的等高模型【难度】2 星【题型】解答【解析】3 个，△AEC、△BED、△DEC．【解析】【答案】3 个，△AEC、△BED、△DEC．【巩固】如图，在梯形 ABCD 中，共有八个三角形，其中面积相等的三角形共有哪几对？ A D O 【考点】三角形的等高模型【难度】2 星【题型】解答【解析】 △ABD 与△ACD，△ABC 与△DBC，△ABO 与△DCO．【答案】△ABD 与△ACD，△ABC 与△DBC，△ABO 与△DCO B C 【例 8】如图，三角形 ABC 的面积为 1，其中 AE  3 AB ， BD A B C E A D 【考点】三角形的等高模型【难度】2 星【题型】解答【关键词】迎春杯【解析】连接 CE ，∵ BC 3 AE  ，∴ ，∴  2 S V 4 ． BCE  BE 2 S V AB S V BD  2  2 S V ABC BDE BCE AB ， 4 S  V ACB 又∵ 【答案】4 BC ，三角形 BDE 的面积是多少？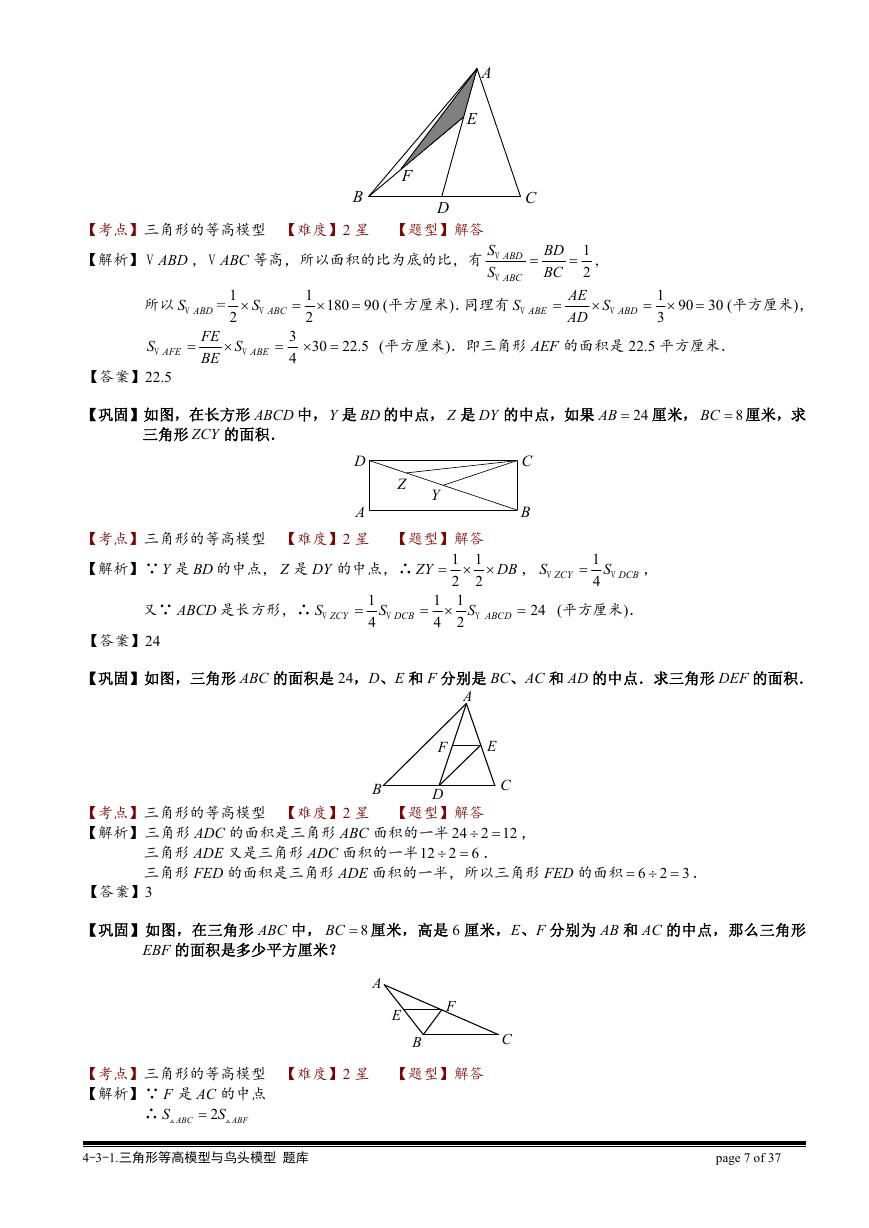 E 2  B C D 【例 9】如右图，AD DB ，AE EF FC  ，已知阴影部分面积为 5 平方厘米， ABC  的面积是平方厘米． B D B D A E F C A E F C 【考点】三角形的等高模型【难度】2 星【题型】解答【关键词】2008 年，四中考题【解析】连接 CD ．根据题意可知， DEF 的面积为 DAC  面积的 1 1 2 3 1 6 以 DEF  15   6 30 (平方厘米)．【答案】30 的面积为 ABC   ．而 DEF  的面积为 5 平方厘米，所以 ABC 的面积为面积的 1 3 ， DAC 的面积为 ABC 面积的 1 2 ，所【巩固】图中三角形 ABC 的面积是 180 平方厘米，D 是 BC 的中点，AD 的长是 AE 长的 3 倍，EF 的长是 BF 长的 3 倍．那么三角形 AEF 的面积是多少平方厘米？ 4-3-1.三角形等高模型与鸟头模型题库 page 6 of 37

A E B F D 【考点】三角形的等高模型【难度】2 星【题型】解答【解析】 ABD 等高，所以面积的比为底的比，有， ABC V V C S V S V ABD ABC  BD BC SV 所以 ABD FE BE S V  = 1 2 S  V S V ABC  ABE 3 4  1 180 90   2 30  22.5  AFE 【答案】22.5  1 2 AE AD ,  S V ABD 1 90 30   3  (平方厘米)， (平方厘米)．同理有 S V  ABE (平方厘米)．即三角形 AEF 的面积是 22.5 平方厘米．【巩固】如图，在长方形 ABCD 中，Y 是 BD 的中点， Z 是 DY 的中点，如果三角形 ZCY 的面积． AB  厘米， 24 BC  厘米，求 8 D A Z Y C B 【考点】三角形的等高模型【难度】2 星【题型】解答 1 【解析】∵Y 是 BD 的中点， Z 是 DY 的中点，∴ 2 ZY    ， DB S V ZCY S V ， DCB 1 4 又∵ ABCD 是长方形，∴ S V  ZCY 【答案】24 S Y ABCD  24 (平方厘米)． 1 2 1   2 1 4 1 4 S V DCB 【巩固】如图，三角形 ABC 的面积是 24，D、E 和 F 分别是 BC、AC 和 AD 的中点．求三角形 DEF 的面积． A F E 【考点】三角形的等高模型【难度】2 星【题型】解答【解析】三角形 ADC 的面积是三角形 ABC 面积的一半 24 2 12   ， B D C 三角形 ADE 又是三角形 ADC 面积的一半12 2 6 三角形 FED 的面积是三角形 ADE 面积的一半，所以三角形 FED 的面积 6 2 3   ．    ．【答案】3 【巩固】如图，在三角形 ABC 中， BC  厘米，高是 6 厘米，E、F 分别为 AB 和 AC 的中点，那么三角形 8 EBF 的面积是多少平方厘米？ A F E B C 【考点】三角形的等高模型【难度】2 星【题型】解答【解析】∵ F 是 AC 的中点 ∴ S  ABC 2 S  ABF 4-3-1.三角形等高模型与鸟头模型题库 page 7 of 37

同理 S ∴ 【答案】6  S  BEF ABF S 2 S  ABC  BEF       4 8 6 2 4 6 (平方厘米)．【例 10】如图所示， A 、 B 、 C 都是正方形边的中点，△ COD 比△ AOB 大15 平方厘米。△ AOB 的面积为平方厘米。【考点】三角形的等高模型【难度】3 星【题型】解答【关键词】走美杯，5 年级，决赛，第 8 题，10 分 15 S 【解析】  【答案】7.5 cm COD BCD ABD ABO ABD      S S S S     2 ，所以， S  ABO  7.5 cm 2 。【例 11】如图 ABCD 是一个长方形，点 E、F 和 G 分别是它们所在边的中点．如果长方形的面积是 36 个平方单位，求三角形 EFG 的面积是多少个平方单位． D G D C E A F B G C F B E A 【考点】三角形的等高模型【难度】2 星【题型】解答【解析】如右图分割后可得，【答案】9   ABCD DEFC EFG 2  矩形矩形 S S S    4 36 4 9   （平方单位）．【巩固】如图，长方形 ABCD 的面积是1 ， M 是 AD 边的中点， N 在 AB 边上，且 2AN BN .那么，阴影部分的面积是多少？ A N B M D C A N B M D C 【考点】三角形的等高模型【难度】3 星【题型】解答【关键词】迎春杯，决赛【解析】连接 BM ，因为 M 是中点所以 ABM△ 又因为 2AN BN ，所以 BDC△ 的面积为的面积为 1 4   ，又因为 BDC△ 1 12 1 1 4 3 5 12 【答案】面积为 1 2 ，所以阴影部分的面积为： 1 12 1    1 2 5 12 . 【例 12】如图，大长方形由面积是 12 平方厘米、24 平方厘米、36 平方厘米、48 平方厘米的四个小长方形组合而成．求阴影部分的面积． 4-3-1.三角形等高模型与鸟头模型题库 page 8 of 37

分享到：

赞收藏

资料库

4-3-1 三角形等高模型与鸟头模型（一）.教师版.doc

相关推荐

小学奥数

热门标签

最新资料