6-1-25 周期问题.学生版.doc-资料库

第1页 / 共10页

第2页 / 共10页

第3页 / 共10页

第4页 / 共10页

第5页 / 共10页

第6页 / 共10页

第7页 / 共10页

第8页 / 共10页

周期问题教学目标 1. 掌握各种周期问题的求解方法． 2. 培养学生观察、分析和逻辑推理能力。知识精讲知识点说明：周期问题：周期现象：事物在运动变化过程中，某些特征有规律循环出现；周期：我们把连续两次出现所经过的时间叫周期；解决有关周期性问题的关键是确定循环周期. 分类： 1．图形中的周期问题； 2．数列中的周期问题； 3．年月日中的周期问题．周期性问题的基本解题思路是：首先要正确理解题意，从中找准变化的规律，利用这些规律作为解题的依据；其次要确定解题的突破口。主要方法有观察法、逆推法、经验法等。主要问题有年月日、星期几问题等。 ⑴观察、逆推等方法找规律，找出周期．确定周期后，用总量除以周期，如果正好有整数个周期，结果就为周期里的最后一个；例如：1，2，1，2，1，2，…那么第 18 个数是多少？这个数列的周期是 2，18 2 9   ，所以第 18 个数是 2． ⑵如果比整数个周期多 n 个，那么为下个周期里的第 n 个；例如：1，2，3，1，2，3，1，2，3，…那么第 16 个数是多少？这个数列的周期是 3，16 3 5 ⑶如果不是从第一个开始循环，可以从总量里减掉不是循环的个数后，再继续算．例如：1，2，3，2，3，2，3，…那么第 16 个数是多少？这个数列从第二个数开始循环，周期是 2， (16 1) 2 7     ，所以第 16 个数是 2． 1    ，所以第 16 个数是 1． 1 例题精讲板块一、图形中的周期问题【例 1】小兔和小松鼠做游戏，他们把黑、白两色小球按下面的规律排列： ●●○●●○●●○… 你知道它们所排列的这些小球中，第 90 个是什么球？第 100 个又是什么球呢？【巩固】美美有黑珠、白珠共 102 个，她想把它们做成一个链子挂在自己的床头上，她是按下面的顺序排列的： ○●○○○●○○○●○○○…… 那么你知道这串珠子中，最后一个珠子应是什么颜色吗？美美怕这种颜色的珠子数量不够，你能帮她算出这种颜色在这串珠子中共有多少个吗？ 6-1-12.周期问题.题库学生版 page 1 of 10

【巩固】黑珠、白珠共 101 颗，穿成一串，排列如下图。这串珠子中，最后一颗珠子应该是_____色的, 这种颜色的珠子在这串中共有_____颗. 【巩固】 ★○○○★★○○○★★○○○……这样的一排图形中第 87 个是什么图形，在 87 个图形中一共有多少个五角星？【例 2】甲、乙、丙三个网站定期更新，甲网站每隔一天更新 1 次；乙网站每隔两天更新 1 次，丙网站每隔三天更新 1 次。在一个星期内，三个网站最多更新次。【例 3】小倩有一串彩色珠子，按红、黄、蓝、绿、白五种颜色排列． ⑴第 73 颗是什么颜色的？ ⑵第 10 颗黄珠子是从头起第几颗？ ⑶第 8 颗红珠子与第 11 颗红珠子之间（不包括这两颗红珠子）共有几颗珠子？【巩固】在一根绳子上依次穿 2 个红珠、2 个白珠、5 个黑珠，并按此方式反复，如果从头开始数，直到第 50 颗，那么其中白珠有多少颗？【例 4】节日的夜景真漂亮，街上的彩灯按照 5 盏红灯、再接 4 盏蓝灯、再接 1 盏黄灯，然后又是 5 盏红灯、4 盏蓝灯、1 盏黄灯、……这样排下去．问： ⑴第 150 盏灯是什么颜色？ ⑵前 200 盏彩灯中有多少盏蓝灯？【巩固】节日的校园内挂起了一盏盏小电灯，小明看出每两个白灯之间有红、黄、绿各一盏彩灯．也就是说，从第一盏白灯起，每一盏白灯后面都紧接着有 3 盏彩灯．那么第 73 盏灯是什么颜色的灯？ 6-1-12.周期问题.题库学生版 page 2 of 10

【巩固】按下面的摆法，摆一百个三角形，请问第 100 个三角形是什么颜色的？在这 100 个三角形中有多少个白色的三角形？ △△△▲▲▲△△△▲▲▲△△△▲▲▲…… 【巩固】流水线上给小木球涂色的次序是：先 5 个红、再 4 个黄、再 3 个绿、在 2 个黑、再 1 个白，然后又依次是 5 红、4 黄、3 绿、2 黑、1 白……如此继续涂下去，到第 2003 个小球该涂什么颜色？【例 5】奥运会就要到了，京京特意做了一些“北京欢迎你”的条幅，这些条幅连起来就成了：“北京欢迎你北京欢迎你北京欢迎你……”依次排列，第 28 个字是什么字？【巩固】在图所示的表中，将每列上、下两个字组成一组，例如第一组为（新奥），第二组为（北林），那么第 50 组是什么？新北京新奥运新北京新奥运新北京新奥运…… 奥林匹克运动会奥林匹克运动会奥林匹克运动会…… 【例 6】小莉把平时积存下来的 200 枚硬币按 3 个 1 分，2 个 2 分，1 个 5 分的顺序排列起来． ⑴最后 1 枚是几分硬币 ⑵这 200 枚硬币一共价值多少钱？【巩固】桌子上摆了很多硬币，按一个一角，两个五角，三个一元的次序排列，一共 19 枚硬币．问：最后一个是多少钱的？第十四个是多少钱的？【例 7】有 249 朵花，按 5 朵红花，9 朵黄花，13 朵绿花的顺序轮流排列，最后一朵是什么颜色的花？这 249 朵花中，什么花最多，什么花最少？最少的花比最多的花少几朵？【巩固】如图所示，每列上、下两个字（字母）组成一组，例如，第一组是“我，A ”，第二组是“们，B ”…… 我们爱科学我们爱科学我 …… D …… A D G A B E F B C C ⑴写出第 62 组是什么？ ⑵如果“爱， C ”代表 1991 年，那么“科， D ”代表 1992 年……问 2008 年对应怎样的组？ 6-1-12.周期问题.题库学生版 page 3 of 10

【例 8】如右图，是一片刚刚收割过的稻田，每个小正方形的边长是 1 米，A、B、C 三点周围的阴影部分是圆形的水洼。一只小鸟飞来飞去，四处觅食，它最初停留在 0 号位，过了一会儿，它跃过水洼，飞到关于 A 点对称的 1 号位；不久，它又飞到关于 B 点对称的 2 号位；接着，它飞到关于 C 点对称的 3 号位，再飞到关于 A 点对称的 4 号位，……，如此继续，一直对称地飞下去。由此推断，2004 号位和 0 号位之间的距离是多少米？板块二、数列中的周期问题【例 9】小和尚在地上写了一列数：7，0，2，5，3，7，0，2，5，3… 你知道他写的第 81 个数是多少吗？你能求出这 81 个数相加的和是多少吗？【巩固】根据下面一组数列的规律求出 51 是第几个数？ 1、2、3、4、6、7、8、9、11、12、13、14、16、17…… 【巩固】如右图所示的数表中，从左往右依次看作五列，第 99 行右边第一个数是几？【巩固】某个早晨,容器中有 200 个细菌,白天有光照,容器中的细菌将减少 65 个,夜间无光照,容器中的细菌将增加 40 个.则在第几个白天,容器中的细菌全部死亡！【例 10】⑴ 4 4  …… 4 （25 个 4），积的个位数是几？ ⑵24 个 2 相乘，积末位数字是几？【巩固】紧接着 1989 后面写一串数字，写下的每一个数字都是它前面两个数字的乘积的个位数．例如，   ，在 2 后面写 8……得到一串数字：19892868…，问：这串   ，在 9 后面写 2，9 2 18 8 9 72 数字从 1 开始，往右数，第 l999 个数字是几？这 1999 个数字的和是多少？ 6-1-12.周期问题.题库学生版 page 4 of 10

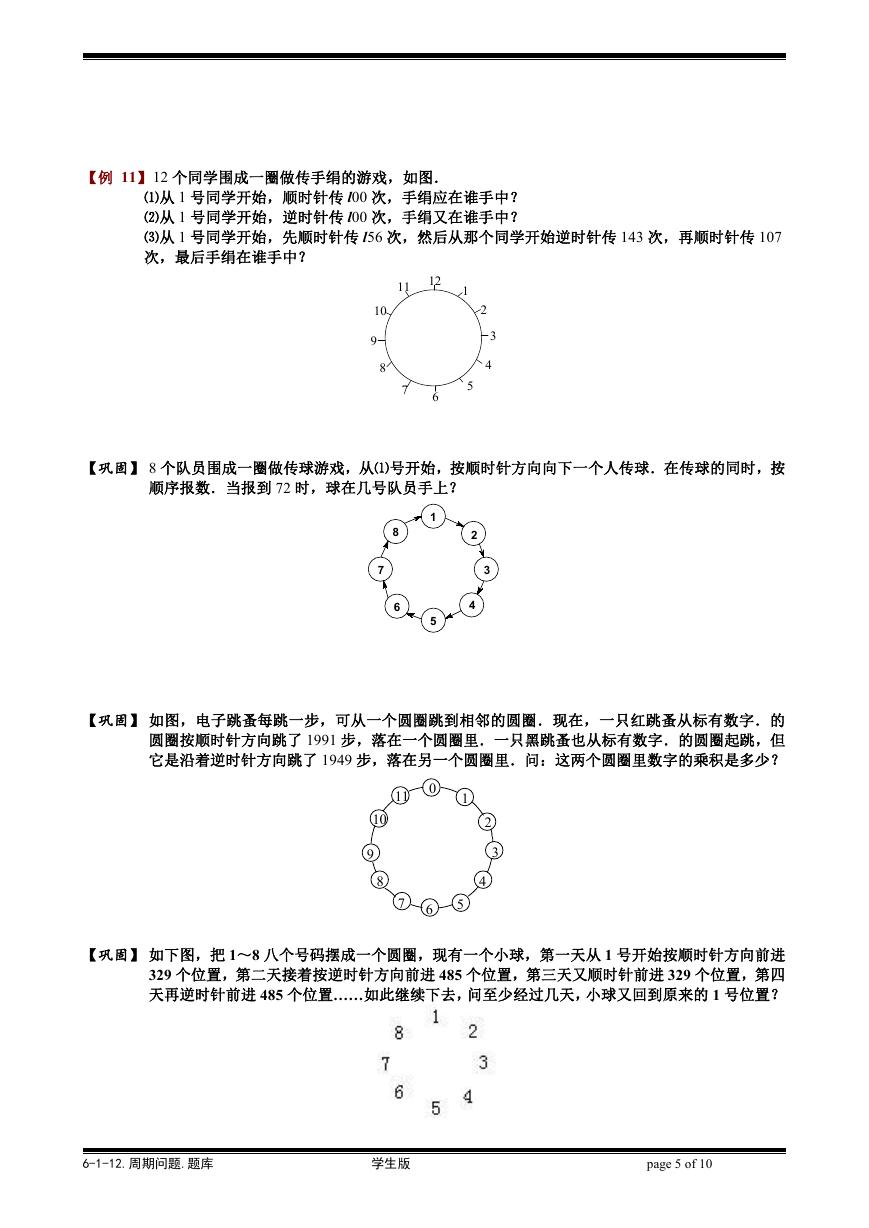
【例 11】12 个同学围成一圈做传手绢的游戏，如图． ⑴从 1 号同学开始，顺时针传 l00 次，手绢应在谁手中？ ⑵从 1 号同学开始，逆时针传 l00 次，手绢又在谁手中？ ⑶从 1 号同学开始，先顺时针传 l56 次，然后从那个同学开始逆时针传 143 次，再顺时针传 107 次，最后手绢在谁手中？ 10 9 8 12 11 1 7 6 5 2 3 4 【巩固】 8 个队员围成一圈做传球游戏，从⑴号开始，按顺时针方向向下一个人传球．在传球的同时，按顺序报数．当报到 72 时，球在几号队员手上？ 7 8 6 1 5 2 4 3 【巩固】如图，电子跳蚤每跳一步，可从一个圆圈跳到相邻的圆圈．现在，一只红跳蚤从标有数字．的圆圈按顺时针方向跳了 1991 步，落在一个圆圈里．一只黑跳蚤也从标有数字．的圆圈起跳，但它是沿着逆时针方向跳了 1949 步，落在另一个圆圈里．问：这两个圆圈里数字的乘积是多少？ 10 9 8 0 11 1 7 6 5 2 3 4 【巩固】如下图，把 1～8 八个号码摆成一个圆圈，现有一个小球，第一天从 1 号开始按顺时针方向前进 329 个位置，第二天接着按逆时针方向前进 485 个位置，第三天又顺时针前进 329 个位置，第四天再逆时针前进 485 个位置……如此继续下去，问至少经过几天，小球又回到原来的 1 号位置？ 6-1-12.周期问题.题库学生版 page 5 of 10

【巩固】如下图，有 16 把椅子摆成一个圆圈，依次编上从 1 到 16 的号码.现在有一人从第 1 号椅子顺时针前进 328 个，再逆时针前进 485 个，又顺时针前进 328 个，再逆时针前进 485 个，又顺时针前进 136 个，这时他到了第几号椅子？【例 12】甲、乙两人对一根 3 米长的木棍涂色。首先，甲从木棍的端点开始涂黑色 5 厘米，间隔 5 厘米不涂色，再涂 5 厘米黑色，这样交替做到底。然后，乙从木棍同一端点开始留出 6 厘米不涂色，然后涂 6 厘米黑色，再间隔 6 厘米不涂色，交替做到底，最后木棍上没有被涂黑色部分的总长度是多少？【例 13】右图中，任意三个连续的小圆圈内三个数的连乘积都是 891，那么 B 代表多少？【巩固】课外活动时，甲、乙、丙、丁四人排成一个圆圈依次报数．甲报“1”，乙报“2”，丙报“3”，丁报 “4”，这样每人报的数总比前一个人多 1．问“34”是谁报的？“71”是谁报的？【巩固】同学们在科技馆参加活动，谁最先参加游戏呢？同学们想了个好办法，大家排成一排 1～2 报数，报 2 的同学再 1～2 报数，这样依次进行下去，最后报 2 的这名同学先玩，如果这列一共有 12 人，最先玩的同学是这一列中的第几个？【巩固】 1999 名同学从前往后排成一列，按下面的规则报数：如果某名同学报的数是一位数，那么后一个同学就要报出这个数与 9 的和；如果某名同学报的数是两位数，那么后一个同学就要报出这个数的个位数与 6 的和。现让第一个同学报 1，那么最后一名同学报的数是( )。【例 14】某班 43 名同学围成一圈。由班长起从 1 开始连续报数，谁报到 100，谁就表演一个节目；然后再由这个同学起从 1 开始连续报数，结果第一个表演节目的是小明，第二个演节目的是小强。那么小明和小强之间有________名同学。 6-1-12.周期问题.题库学生版 page 6 of 10

【例 15】实验室里有一只特别的钟，一圈共有 20 个格．每过 7 分钟，指针跳一次，每跳一次就要跳过 9 个格，今天早晨 8 点整的时候，指针恰好从 0 跳到 9，问：昨天晚上 8 点整的时候指针指着几？【巩固】有 A 、B 、C 三个蜂鸣器，每次持续鸣叫的时间比例是 3: 4 :5 ．每个蜂鸣器每次鸣叫完后停 8 秒钟又开始鸣叫．最初三个蜂鸣器同时开始鸣叫，14 分钟后第二次同时开始鸣叫，此时 B 蜂鸣器已是第 43 次鸣叫了．问：最初同时开始鸣叫后的多少秒 A 与 C 第一次同时结束鸣叫？【例 16】有一个 111 位数，各位数字都是 1，这个数除以 6，余数是几？商的末位数字是几？【巩固】有一个 1111 位数，各位数字都是 1，这个数除以 6，余数是几？商的末位数字是几？【例 17】求 128 28 29 29 的个位数字. 【巩固】算式（ 367 367  762 762  ） 123 的得数的尾数是几？ 123 板块三、日期中的周期问题【例 18】阳历 1978 年 1 月 1 日是星期日，阳历 2000 年 1 月 1 日是星期几？ 6-1-12.周期问题.题库学生版 page 7 of 10

【巩固】 1999 年的元旦是星期五，那么据此你知道 2005 年的元旦是星期几吗？【巩固】小童的生日是 6 月 27 日，这一年的 6 月 1 日是星期六，小童的生日是星期几呢？【巩固】今天是星期三，那么从明天起第 365 天是星期几？【例 19】2002 年的 6 月 1 日是星期六，那么这一年的 10 月 1 日是星期几呢？【巩固】 2008 年 3 月 3 号是星期一，算一算 2008 年 8 月 8 号奥运会开幕是星期几？【巩固】 2008 年的“六·一”儿童节是星期日，2008 年的“十·一”是星期几？【例 20】某部 84 集的电视连续剧在某星期日开播，从星期一到星期五以及星期日每天都要播出 1 集，星期六停播．问：最后一集在星期几播出? 【巩固】某人连续打工 24 天，赚得 190 元(日工资 10 元，星期六做半天工，发半工资，星期日休息，无工资)．已知他打工是从 1 月下旬的某一天开始的，这个月的 1 号恰好是星期日．问：这人打工结束的那一天是 2 月几日? 6-1-12.周期问题.题库学生版 page 8 of 10

资料库

6-1-25 周期问题.学生版.doc

相关推荐

小学奥数

热门标签

最新资料