4-5-2 长方体与正方体（二）.教师版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：2.10M 资料格式：doc 举报版权申诉

第1页 / 共38页

第2页 / 共38页

第3页 / 共38页

第4页 / 共38页

第5页 / 共38页

第6页 / 共38页

第7页 / 共38页

第8页 / 共38页

即：(毫升)．

长方体与正方体（二）对于小学几何而言，立体图形的表面积和体积计算，既可以很好地考查学生的空间想象能力，又可以具体考查学生在公式应用中处理相关数据的能力，所以，很多重要考试都很重视对立体图形的考查．例题精讲如右图，长方体共有六个面(每个面都是长方形)，八个顶点，十二条棱． ①在六个面中，两个对面是全等的，即三组对面两两全等． (叠放在一起能够完全重合的两个图形称为全等图形．) ②长方体的表面积和体积的计算公式是： ) 长方体的表面积：长方体的体积：V ③正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形．如果它的棱长为 a ，那么：长方体与正方体的体积 2( ab bc  abc ． 26 a 3 a  ca ；， V 正方体 S 正方体 S 长方体．   长方体立体图形的体积计算常用公式：立体图形示例体积公式相关要素  V abh V Sh 3 V a V Sh 三要素： a 、 b 、 h 二要素： S 、 h 一要素： a 二要素： S 、 h 长方体正方体不规则形体的体积常用方法： ①化虚为实法 ②切片转化法 ③先补后去法 ④实际操作法 ⑤画图建模法【例 1】一个长方体的棱长之和是 28 厘米，而长方体的长宽高的长度各不相同，并且都是整厘米数，则长方体的体积等于立方厘米。 4-5-2.长方体与正方体（二）题库 page 1 of 38

【考点】长方体与正方体【难度】2 星【题型】填空【关键词】希望杯， 6 年级，第 16 题，6 分【解析】由题意知长、宽、高的和为 28 4 7 2、4，所以体积为 8 立方厘米【答案】8   ，又根据题意长、宽、高各不相同，且是整数，所以只能是 1、【例 2】将几个大小相同的正方体木块放成一堆，从正面看到的视图是图（a），从左向右看到的视图是图（b），从上向下看到的视图是图（c），则这堆木块最多共有___________块。【考点】长方体与正方体【难度】2 星【题型】填空【关键词】希望杯，4 年级，初赛，8 题【解析】对于图 c 来说，每个小方块都摞了 2 层，最多有 6 块。【答案】6 【例 3】一根长方体木料，体积是 0.078 立方米．已知这根木料长1.3 米．宽为 3 分米，高该是多少分米?孙健同学把高错算为 3 分米．这样，这根木料的体积要比 0.078 立方米多多少? 【考点】长方体与正方体【难度】2 星【题型】解答【关键词】小数报，决赛【解析】 0.078 (1.3 0.3) 0.2 (米)．    0.2 米  2 分米． 1.3 0.3 0.3 0.078 0.039 所以这根木料的高是 2 分米；算错后，这根木料的体积比 0.078 立方米多 0.039 立方米． (立方米)．     【答案】0.039 【例 4】如图，两个同样的铁环连在一起长 28 厘米，每个铁环长 16 厘米。8 个这样的铁环依此连在一起长厘米。【考点】长方体与正方体【难度】3 星【题型】填空【关键词】希望杯，四年级，复赛，第 10 题，4 分【解析】两个铁环连在一起，重叠的部分长 16×2-28＝4 厘米，8 个这样的铁环依此连在一起长 16×8-4×7＝100 厘米。【答案】100 【例 5】某工人用薄木板钉成一个长方体的邮件包装箱，并用尼龙编织条(如图所示)在三个方向上的加固．所用尼龙编织条分别为 365 厘米，405 厘米，485 厘米．若每个尼龙加固时接头重叠都是 5 厘米．问这个长方体包装箱的体积是多少立方米? 【考点】长方体与正方体【难度】3 星【题型】解答【关键词】华杯赛，决赛，口试【解析】长方体中 4-5-2.长方体与正方体（二）题库 page 2 of 38

 ，  ，  ，    2 2 2 高  宽 1 (365 5) 180 高  长 1 (405 5) 200 长  宽 1 (485 5) 240 ⑵  ⑴：长  宽 20 ， ⑷  ⑶：长 130 代入⑴得高 70 ．所以长方体体积为 70 110 130 1001000    ，从而宽 110  ， (立方厘米) 1.001   【答案】1.001 ⑴ ⑵ ⑶ ⑷ (立方米) 【例 6】某工人用木板钉成一个长方体邮件包装箱，并用三根长度分别为 235 厘米、445 厘米、515 厘米的尼龙带进行加固（如下图），若每根尼龙带加固时截头重叠都是 5 厘米，那么这个长方体包装箱的体积是立方米。【考点】长方体与正方体【难度】3 星【题型】填空【关键词】迎春杯，高年级，初赛，9 题【解析】长方形的长为： 长方形的宽为: 长方形的高为： 长方形的体积为:  445 515 235 5    2 75 515 5 180 2     235 5 75 2 2 40    6 180 75 40 10 0.54          4 180  （厘米）；（厘米）；（立方米）。（厘米）；【答案】0.54 【例 7】一个长方体的表面积是 33.66 平方分米，其中一个面的长是 2.3 分米，宽是 2.1 分米，它的体积是 _____立方分米. 【考点】长方体与正方体【难度】3 星【题型】填空【关键词】迎春杯【解析】长方体的高是 (33.66 2.1 2.3 2) 2 (2.1 2.3)       长方体的体积是 2.1 2.3   【答案】 19 110 13 30 11  13 19 110 (立方分米)．  30 11 (分米). 【例 8】把一根长 2.4 米的长方体木料锯成 5 段(如图)，表面积比原来增加了 96 平方厘米．这根木料原来的体积是_____立方厘米． 2.4米【考点】长方体与正方体【难度】3 星【题型】填空【关键词】迎春杯，决赛【解析】 96 8 12 (平方厘米)，  12 240 2880 所以这根木料原来的体积为 2880 立方厘米． (立方厘米)．    【答案】2880 4-5-2.长方体与正方体（二）题库 page 3 of 38

【例 9】一个长方体的宽和高相等，并且都等于长的一半(如图)．将这个长方体切成 12 个小长方体，这些小长方体的表面之和为 600 平方分米．求这个大长方体的体积．【考点】长方体与正方体【难度】3 星【题型】解答【关键词】小数报，决赛【解析】设大长方体的宽(高)为 a 分米，则长为 2a ，右(左)面积为 2a ，其余面的面积为 22a ，根据题意， 2 a  2 8 a 2 2  大长方体的体积 2 5 5 5 250      6 2   600 所以 2 25 a  ， 5a  ． (立方分米)． 2 a  【答案】250 【例 10】有三个大小一样的正方体，将接触的面用胶粘接在一起成图示的形状，表面积比原来减少了 16 平方厘米.求所成形体的体积. 【考点】长方体与正方体【难度】3 星【题型】解答【解析】三个小正方体拼接成图中的样子，减少了小正方体的 4 个侧面正方形的面积，表面积减少了 16 平方   平方厘米，每个正方体棱长为 2 厘米，三个小正方体体积(即所成厘米，每个正方形侧面为16 4 4 形体的体积)是 3  立方厘米. 3 2  24 【答案】24 【例 11】小明在桌面上摆了一些大小一样的正方体木块，摆完后从正面看如左下图，从侧面看如右下图，那么他最多用了_____块木块，最少用了____ __块木块。【考点】长方体与正方体【难度】3 星【题型】填空【关键词】走美杯，五年级，决赛，第 8 题，10 分【解析】从上往下看，分别如左下图和右下图所示(图中数字为每一格的木块数)。【答案】最多 25，最少 9 【例 12】边长为 5 的正方形，被分割成 5 5 的小方格。每个小方格上堆放边长为1cm 的正方体积木，个数如图所示。在每个积木外露的面上贴一张红纸，其它面（与其它积木块或方格纸相接的面）不贴。共贴张红纸。恰贴 3 张红纸的有块积木。 4-5-2.长方体与正方体（二）题库 page 4 of 38

【考点】长方体与正方体【难度】4 星【题型】填空【关键词】走美杯，4 年级，决赛，第 11 题，12 分【解析】从正面看，需要贴 5 5 25   （张）；      （张）；      （张）；      （张）；      （张）；从左边看，需要贴 5 4 5 5 5 24 从右边看，需要贴 5 4 5 5 5 24 从前面看，需要 5 5 4 5 5 24 从后面看，需要 5 5 4 5 5 24 再看中间凹进去的部分，需要贴 6 4 4 2 2 4 4 所以一共需要贴 25 24 24 24 24 26 147 先看四条边上，有14 块积木贴 3 张红纸；非边上的积木，有1块积木恰好贴 3 张，所以一共有14 1 15   （块）积木。     （张）；          （张）， 26 【答案】共贴 26 张，共有 15 块【例 13】有一个长方体，长是宽的 2 倍，宽是高的 3 倍；长的 1 2 与高的 1 3 之和比宽多 1 厘米．这个长方体的体积是立方厘米．【考点】长方体与正方体【难度】3 星【题型】填空【关键词】迎春杯【解析】长的 1 3 9 18 486   2 即宽，所以高的 1 (立方厘米)．  【答案】486 3 就是 1 厘米，高是 3 厘米，宽是 3 3 9   厘米，长是 9 2 18   厘米，体积是【巩固】一个长方体的各条棱长的和是 48 厘米，并且它的长是宽的 2 倍，高与宽相等，那么这个长方体的体积是______ 立方厘米．【考点】长方体与正方体【难度】3 星【题型】填空【关键词】迎春杯，决赛【解析】依题意，这个长方体的长、宽、高之和是 48 4 12      (厘米)， (厘米)，于是它的宽与高都等于12 (2 1 1) 3 它的长是 3 2 6 所以这个长方体的体积是 6 3 3 54   厘米．     (立方厘米)．【答案】54 【例 14】把 11 块相同的长方体的砖拼成如图所示的大长方体，已知每块砖的体积是 288cm ，则大长方体的 3 表面积为多少？【考点】长方体与正方体【难度】4 星【题型】解答【解析】如果知道每块砖的长、宽、高即可求出所有的量，但我们只知道它们的乘积，但可以从图中发现隐含的数量关系． 4-5-2.长方体与正方体（二）题库 page 5 of 38

由图可知每块砖的长、宽、高的比值，两个长等于三个宽，所以长、宽之比为 3: 2 ，四个高等于一个长，所以长、高之比为 4 :1 ，长、宽、高之比为12 :8 : 3 ，设砖的长为 12 单位，那么体积应该为    个立方单位，所以一个单位长度就是 1 厘米，所以大长方体的长、宽、高分别为：24 12 8 3 288 厘米，12 厘米，11 厘米，所以大长方体的表面积为： 24 12 12 11 11 24 平方厘米． 2 1368   ）（      【答案】1368 【例 15】有大、中、小三个正方形水池，它们的内边长分别是 6 米、3 米、2 米．把两堆碎石分别沉没在中、小水池的水里，两个水池的水面分别升高了 6 厘米和 4 厘米．如果将这两堆碎石都沉没在大水池的水里，大水池的水面升高了多少厘米？【考点】长方体与正方体【难度】4 星【题型】解答【解析】把碎石沉没在水中，水面升高所增加的体积，就等于所沉入的碎石的体积．   (米 3)，    因此，沉入水池中的碎石的体积是 3 3 0.06 0.54   而沉入小水池中的碎石的体积是 2 2 0.04 0.16 (米 3)．这两堆碎石的体积一共是 0.54 0.16 0.7 把它们都沉入大水池里，大水池的水面升高所增加的体积也就是 0.7 米 3．而大水池的底面积是 6 6 36   0.7 36 (厘米)  故大水池的水面升高了 171 18 (米 3)．所以水面升高了 171 0.7 36 18 (厘米)． (米 3)．厘米． 70 36 (米)     【答案】 171 18 【例 16】一个正方体容器，容器内部边长为 24 厘米，存有若干水，水深17.2 厘米，现将一些碎铁块放入容器中，铁块沉入水底，水面上升 2.5 厘米，如果将这些铁块铸成一个和容器等高的实心圆柱，重新放入池中，则水面升高几厘米？【考点】长方体与正方体【难度】4 星【题型】解答【解析】设铁块铸成和容器等高的实心圆柱放入池中水面升高 x 厘米，则有水面升高后水的总体积  原来水的体积  铁块浸入水中的体积， 2 24   2.5 S ，得到  (厘米)． 2  其中所以水面升高了19.2 17.2 24  铁块的底面积 24   S x 2 2 24  17.2    【答案】2 铁块的底面积 24 2.5 ，解得 19.2 ， S 铁块的底面积， x  x  【例 17】如图，有一个棱长为 10 厘米的正方体铁块，现已在每两个对面的中央钻一个边长为 4 厘米的正方形孔（边平行于正方体的棱），且穿透．另有一长方体容器，从内部量，长、宽、高分别为 15 厘米、12 厘米、9 厘米，内部有水，水深 3 厘米．若将正方体铁块平放入长方体容器中，则铁块在水下部分的体积为立方厘米．【考点】长方体与正方体【难度】4 星【题型】填空【关键词】迎春杯，初赛，6 年级【解析】可以把正方体铁块看作三层：最下面一层为中央穿孔的长方体，高为 3 厘米；中间一层为 4 个长方体立柱，高为 4 厘米；最上面一层也是高为 3 厘米的中央穿孔的长方体. 由于长方体容器内原有水深 3 厘米，所以正方体铁块放入水中后，铁块最下面一层肯定全部在水中，而水也不可能上升到最上面一层，即恰在中间一层.设水面上升了 h 厘米，则中间一层在水中的部分恰好为 h 厘米. 由于水面上升是由于铁块放入水中导致，水面上升的体积即等于铁块在水下部分的体积，即： 4-5-2.长方体与正方体（二）题库 page 6 of 38

15 12    h 2 (10  2 4 ) 3 3   2 故铁块在水下部分的体积为 15 12  【答案】315   ，解得 7 4 4 h  ， h   315 (立方厘米). 7 4 【例 18】把 1 个棱长是 3 厘米的正方体分割成若干个小的正方体，这些小正方体的棱长必须是整厘米数．如果这些小正方体的体积不要求都相等，那么最少可分割成个小正方体．【考点】长方体与正方体【难度】4 星【题型】填空【关键词】迎春杯，决赛【解析】因为小正方体的棱长只可能是 2 厘米或 1 厘米．必须分割出棱长是 2 厘米的小正方体才能使数量减少．显然，棱长是 3 厘米的正方体只能切割出一个棱长为 2 厘米的小正方体，剩余部分再切割出 (个)小正方 3 3 3 2 2 2 27 8 19       体．   个棱长是 1 厘米的小正方体，这样总共可以分割成1 19 20   【答案】20 【巩固】有一个长方体的盒子，从里面量长 40 厘米，宽 12 厘米，高 7 厘米，在这个盒子里放长 5 厘米，宽 4 厘米，高 3 厘米的长方体木块．最多可放块． 4 3 3 3 3 3 4 4 4 【考点】长方体与正方体【难度】3 星【题型】填空【关键词】祖冲之杯【解析】上图表明 3 4 的长方形可以填满 7 12 的长方形．   的长方体可以填满 40 7 12 于是 5 3 4 40 7 12 (5 3 4) 56      (个)．    的长方体，即盒子中最多可放这种长方体【答案】56 【例 19】有甲、乙、丙 3 种大小的正方体木块，棱长比是1: 2 : 3 ．如果用这三种正方体拼成尽量小的一个正方体，且每种都至少用一个，则最少需要这三种正方体共多少？【考点】长方体与正方体【难度】4 星【题型】解答【解析】设甲的棱长是 1，则乙的棱长是 2，丙的棱长是 3．一个甲种木块的体积是 1，一个乙种木块的体积    ．    ，一个丙种木块的体积是 3 3 3 27 是 2 2 2 8 由于每种正方体都要用到，那么所拼成的正方体的棱长最小应为 3 2 5 当这三种木块拼成的正方体的棱长是 5 时，体积是 5 5 5 125 要想使三种正方体的总数最小，则体积较大的木块应尽可能多．由于棱长为 5，所以其中丙种木块只能有 1 个．有了 1 个丙种木块后，乙种木块最多可以有 4 2 1 7 丙种木块的体积是 27，乙种木块的体积是 8 7 56 甲种木块 42 1 42 所以共需要至少1 7 42 50   ，余下的体积为125 27 56  ．所以还需要    块．    ．   块．  块．   ．   42   【答案】50 【例 20】用1 1 2   、1 1 3 还有 14 块1 1 3 ________块．   、1 2 2   的小木块，如果要拼成 10 个 3 3 3   三种小木块拼成 3 3 3   的正方体．现有足够多的1 2 2   的正方体，则最少需要 1 1 2   的小木块，   的小木块【考点】长方体与正方体【难度】4 星【题型】填空【解析】 1 1 2   、1 2 2   、1 1 3 因为 3 3 3 27 当只用 1 块1 1 3   三种木块的体积分别为 2，3，4，其中只有 3 为奇数，2，4 都是偶数．    ，体积为奇数，所以每个 3 3 3   的正方体中，1 1 3   的木块要有奇数块．   时，剩下的体积为 24，但无法完全用1 2 2   完成，还需要1 1 2   的小木块，由 4-5-2.长方体与正方体（二）题库 page 7 of 38

于 24 和 4 都是 4 的倍数，所以1 1 2 木块．检验可知用 1 块1 1 3 的正方体．当用 3 块1 1 3 拼成．当用 5 块1 1 3 用1 1 2 为了尽量少用1 1 2 以在 8 个 3 3 3 块；也可以在 9 个 3 3 3 的木块．前者需要 2 8 1 2 18 块 18 块．   的小木块拼成．【答案】18   的小木块、2 块1 1 2   的小木块和 5 块1 2 2   的小木块的体积和也是 4 的倍数，至少要用 2 块1 1 2   的小   的小木块可以拼成 3 3 3     的小木块时，体积剩下 18，可以再用 4 块1 2 2   的小木块和 1 块1 1 2   的小木块   的小木块时，体积剩下 12，此时可以再用 3 块1 2 2   的小木块拼成，即此时不需要   的木块，所以要尽量多用其他木块．而一共只有 14 块1 1 3   的正方体中各用 1 块1 1 3   的木块，另 2 个 3 3 3   的正方体各用 3 块1 1 3   的正方体中各用 1 块1 1 3     个，后者需要 2 9 18   的木块，另 1 个 3 3 3   个，数量相同，所以最少需要1 1 2   的木块，所以可   的木   的正方体用 5 块1 1 3     的木【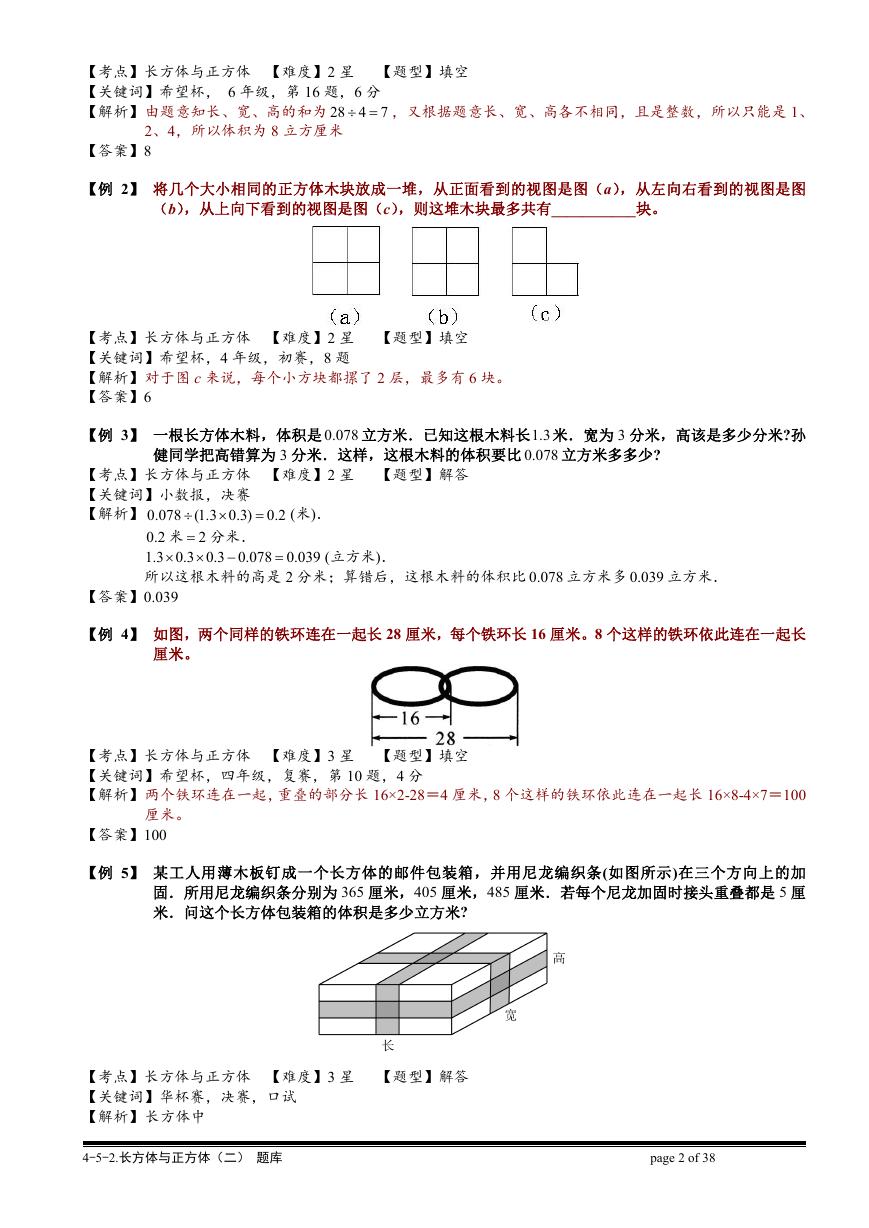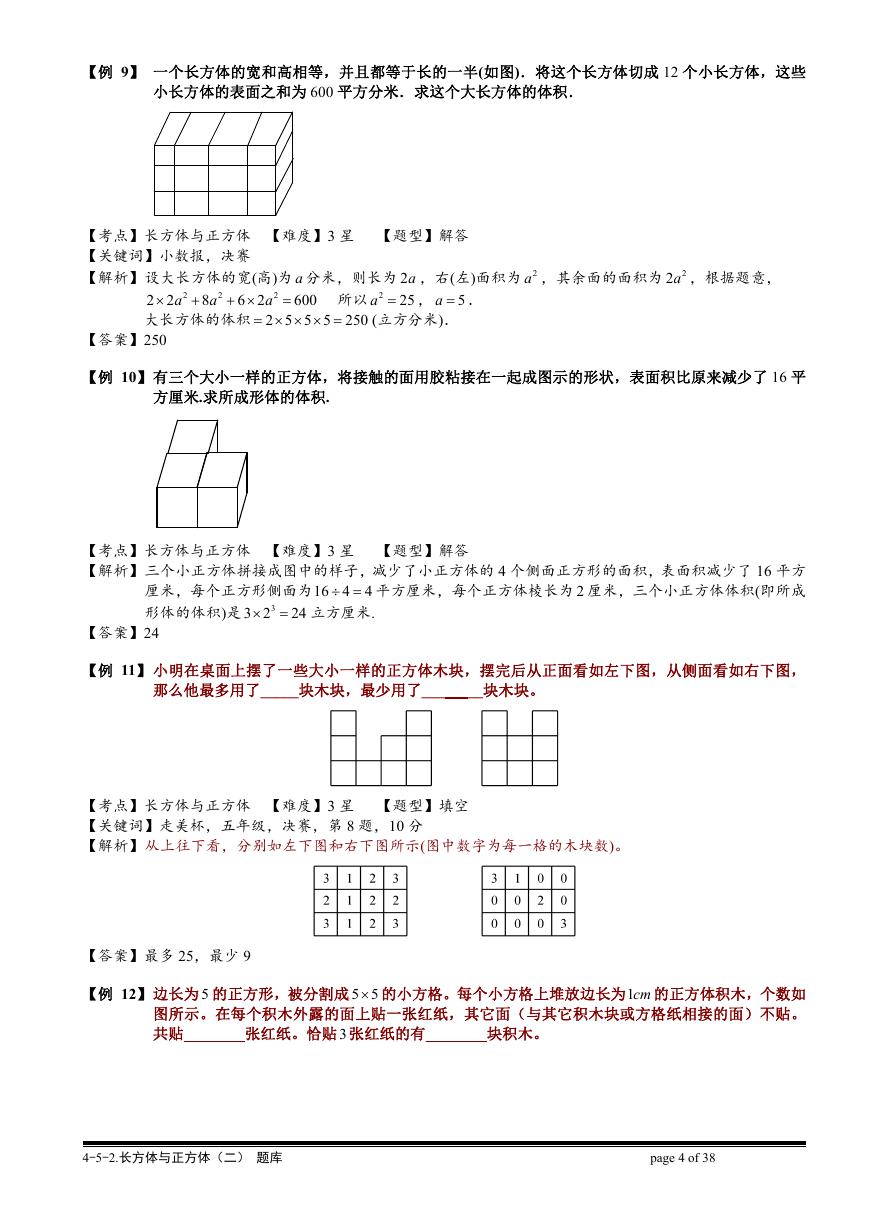例 21】把一个长方体形状的木料分割成 3 小块，使这 3 小块的体积相等．已知这长方体的长为 15 厘米，宽为 12 厘米，高为 9 厘米．分割时要求只能锯两次，如图 1 就是一种分割线的图．除这种分割的方法外，还可有其他不同的分割方法，请把分割线分别画在图 2 的各图中．图 1 【考点】长方体与正方体【难度】4 星【题型】解答【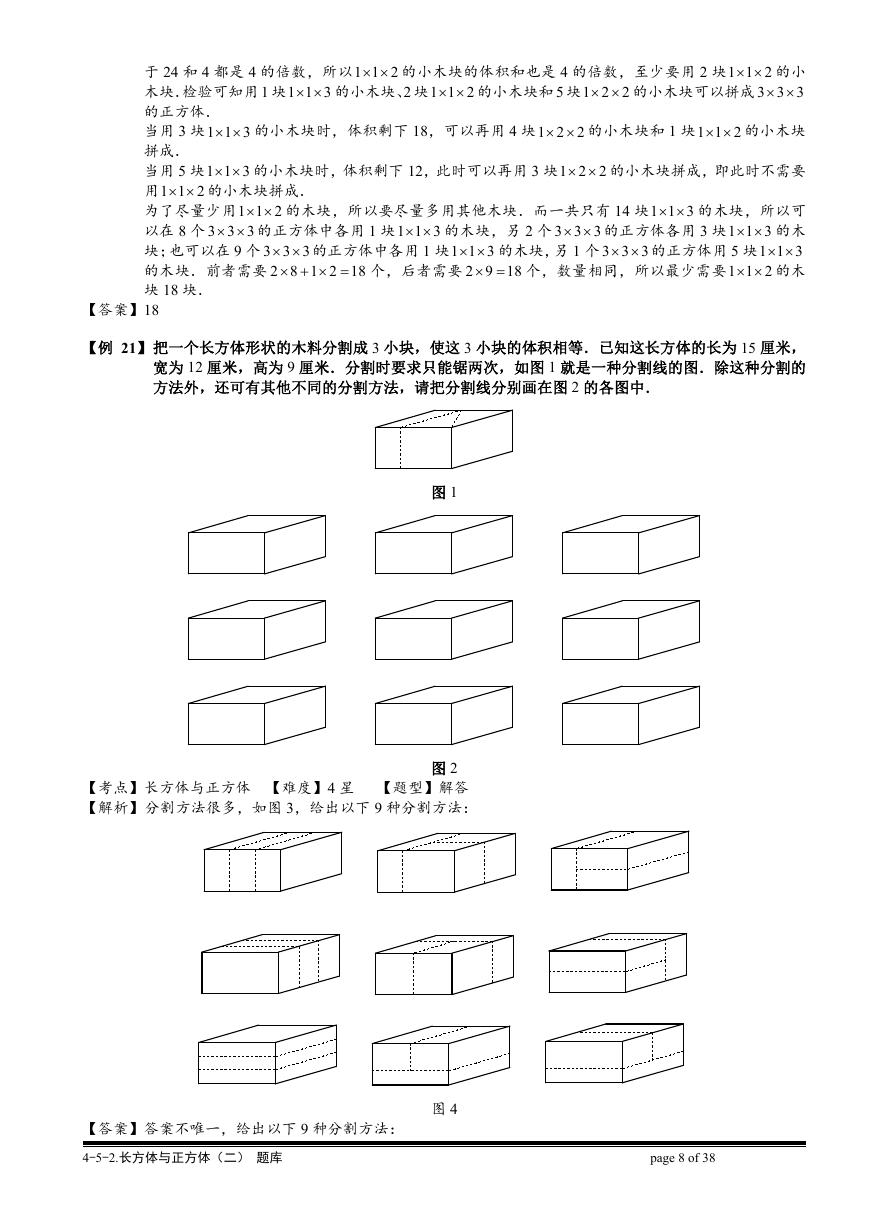解析】分割方法很多，如图 3，给出以下 9 种分割方法：图 2 【答案】答案不唯一，给出以下 9 种分割方法： 4-5-2.长方体与正方体（二）题库图 4 page 8 of 38

分享到：

赞收藏

资料库

4-5-2 长方体与正方体（二）.教师版.doc

相关推荐

小学奥数

热门标签

最新资料