5-1-3-1 数阵图（一）.教师版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：1.38M 资料格式：doc 举报版权申诉

第1页 / 共11页

第2页 / 共11页

第3页 / 共11页

第4页 / 共11页

第5页 / 共11页

第6页 / 共11页

第7页 / 共11页

第8页 / 共11页

文本预览

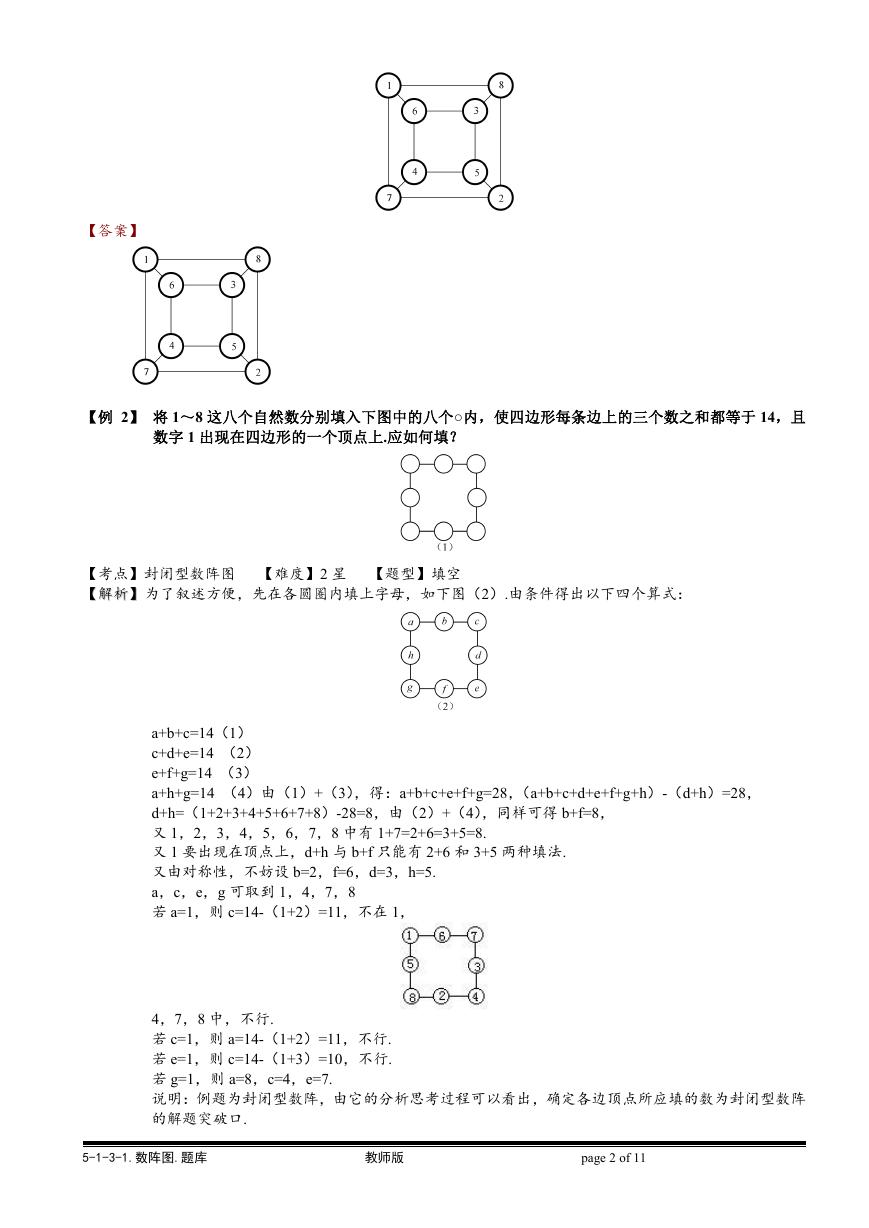
5-1-3-1.数阵图教学目标 1. 了解数阵图的种类 2. 学会一些解决数阵图的解题方法 3. 能够解决和数论相关的数阵图问题知识点拨 . 一、数阵图定义及分类： 1. 定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图. 2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图. 3. 二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手：第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．例题精讲模块一、封闭型数阵图【例 1】把 1～8 的数填到下图中，使每个四边形中顶点的数字和相等。【考点】复合型数阵图【难度】3 星【题型】填空【关键词】学而思杯，3 年级，第 6 题【解析】 5-1-3-1.数阵图.题库教师版 page 1 of 11

【答案】【例 2】将 1～8 这八个自然数分别填入下图中的八个○内，使四边形每条边上的三个数之和都等于 14，且数字 1 出现在四边形的一个顶点上.应如何填？【考点】封闭型数阵图【难度】2 星【题型】填空【解析】为了叙述方便，先在各圆圈内填上字母，如下图（2）.由条件得出以下四个算式：【解析】 a+b+c=14（1） c+d+e=14 （2） e+f+g=14 （3） a+h+g=14 （4）由（1）+（3），得：a+b+c+e+f+g=28，（a+b+c+d+e+f+g+h）-（d+h）=28， d+h=（1+2+3+4+5+6+7+8）-28=8，由（2）+（4），同样可得 b+f=8，又 1，2，3，4，5，6，7，8 中有 1+7=2+6=3+5=8. 又 1 要出现在顶点上，d+h 与 b+f 只能有 2+6 和 3+5 两种填法. 又由对称性，不妨设 b=2，f=6，d=3，h=5. a，c，e，g 可取到 1，4，7，8 若 a=1，则 c=14-（1+2）=11，不在 1， 4，7，8 中，不行. 若 c=1，则 a=14-（1+2）=11，不行. 若 e=1，则 c=14-（1+3）=10，不行. 若 g=1，则 a=8，c=4，e=7. 说明：例题为封闭型数阵，由它的分析思考过程可以看出，确定各边顶点所应填的数为封闭型数阵的解题突破口. 5-1-3-1.数阵图.题库教师版 page 2 of 11

【答案】【例 3】在如图 6 所示的○内填入不同的数，使得三条边上的三个数的和都是 12，若 A、B、C 的和为 18，则三个顶点上的三个数的和是。【考点】封闭型数阵图【难度】1 星【题型】填空【关键词】希望杯，五年级，复赛，第 11 题，5 分【解析】设三个顶点为 D,E,F，求 D,E,F。观察容易发现，三条边的和为 36，即 D+A+E+E+C+F+F+B+D=36 18+2( D+E+F)=36，所以 D+E+F=9 【答案】 9 【例 4】将1 至 6 这六个数字填入图中的六个圆圈中(每个数字只能使用一次)，使每条边上的数字和相等．那么，每条边上的数字和是． a d f 9 b e 8 7 c 9 7 8 【考点】封闭型数阵图【难度】2 星【题型】填空【解析】如图，用字母表示各个圆圈中的数，那么每条边上的数字和为【解析】    ，所以每条边上的数字和最小为 17，最大为 20，如下两图为每条边上的数字和分别为，由于 a b c   最小为1 2 3 6    ，最大为 9 a b c       1 2   4 5 6 15 17 和 20 时的填法．    3 15  a b c   3 1 6 8 5 4 9 2 7 9 3 5 4 2 1 3 8 7 6    ， d ，与题意不符，所以每条边上的数字和不能为 18．如果每条边上的数字和为 19，类似分     ，即而每条边上的数字和能否为 18 或 19 呢？答案是否定的，现说明如下．如果每条边上的数字和为 18，那么得到 c 析可得到 b 所以每条边上的数字和为 17 或 20． e ，也与题意不符，所以每条边上的数字和不能为 19．   ，而  18 15 a b d a b c    a b d 9 18 9   3 9 【答案】17 或 20 【例 5】将 1 到 8 这 8 个自然数分别填入如图数阵中的 8 个圆圈，使得数阵中各条直线上的三个数之和都相等，那么 A 和 B 两个圆圈中所填的数之差(大数减小数)是______． 5-1-3-1.数阵图.题库教师版 page 3 of 11

A B 【考点】封闭型数阵图【难度】3 星【题型】填空【关键词】2008 年，学而思杯，五年级，4 年级，第 4 题【解析】方法一：如图【解析】 a b c A B d e f  ，所以 2A B s 3 c B f s          3 2 A B s A B B        ，而   1 2 ，所以 5 A B         用字母来表示各个圆圈中的数字，设各条直线上的三个数之和都为 s ，那么 a A e b A d f a b c d  ，那么 A 是 3 的倍数.如果 3A  ， a b c d f 得 7B  ；如果 6A  ，得 2B  ，这两种情况下 A 和 B 的差都为 4，所以 A 和 B 两个圆圈中所填的数之差(大数减小数)是 4. 方法二：设各条直线上的三个数之和都为 s ， 2(1 2 3 5 A  8 36   a b c d            ，，即 72      5B  ， 5B s A 3 B 36 e e   8) e s f  ， 2 s ，由于 (1 2 3      8)  3A  s ，即 36  3A  ， s 所以因此有， 2 14 B    s 14 s    6 A 7 13 B    s 13 s    3 A , ,综合有 2 B    14 s   6 A ， 7 B    13 s   3 A ，所以 A 和 B 两个圆圈中所填的数之差(大数减小数)是 4. 【答案】4 【例 6】如图所示，圆圈中分别填人 0 到 9 这 10 个数，且每个正方形顶点上的四个数之和都是 18，则中间两个数 A 与 B 的和是________。【考点】封闭型数阵图【难度】3 星【题型】填空【关键词】希望杯，六年级，二试，第 5 题，4 分【解析】若每个正方形中数的和都是 18，那么总和为 54，而这 10 个数的和为 45，其中 A、B 各多算了一次，故 A+B=9。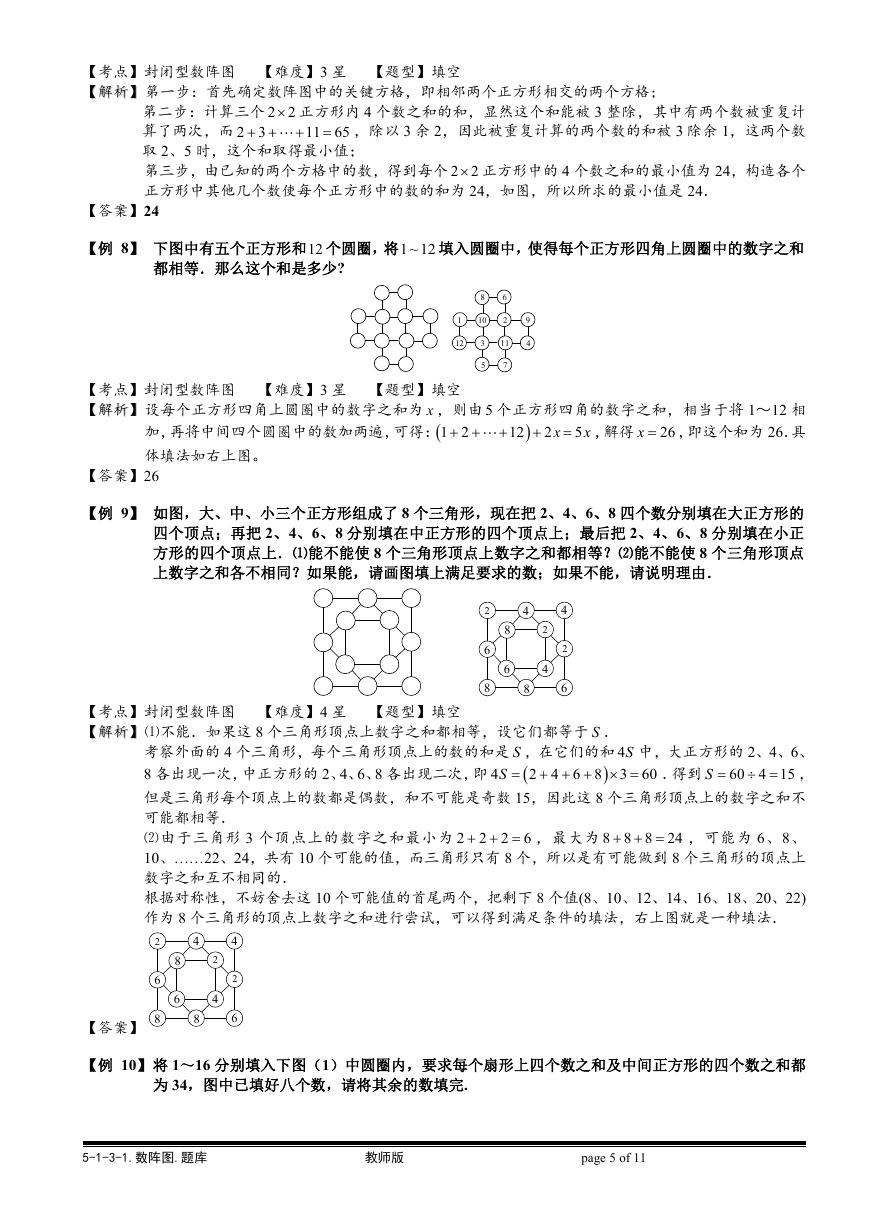【答案】 9 【例 7】把 2～11 这 10 个数填到右图的 10 个方格中，每格内填一个数，要求图中 3 个 2 2 的正方形中的 4 个数之和相等．那么，这个和数的最小值是多少？ 8 11 3 2 10 7 5 9 4 6 5-1-3-1.数阵图.题库教师版 page 4 of 11

【考点】封闭型数阵图【难度】3 星【题型】填空【解析】第一步：首先确定数阵图中的关键方格，即相邻两个正方形相交的两个方格；【解析】   第二步：计算三个 2 2 正方形内 4 个数之和的和，显然这个和能被 3 整除，其中有两个数被重复计，除以 3 余 2，因此被重复计算的两个数的和被 3 除余 1，这两个数算了两次，而 2 3 取 2、5 时，这个和取得最小值；第三步，由已知的两个方格中的数，得到每个 2 2 正方形中的 4 个数之和的最小值为 24，构造各个正方形中其他几个数使每个正方形中的数的和为 24，如图，所以所求的最小值是 24．  11 65  【答案】24 【例 8】下图中有五个正方形和12 个圆圈，将1 ~ 12 填入圆圈中，使得每个正方形四角上圆圈中的数字之和都相等．那么这个和是多少? 1 12 8 10 3 5 6 2 11 7 9 4 【考点】封闭型数阵图【难度】3 星【题型】填空【解析】设每个正方形四角上圆圈中的数字之和为 x ，则由 5 个正方形四角的数字之和，相当于将 1～12 相【解析】 x  ，即这个和为 26．具，解得 26 1 2   5x  12 2   x 加，再将中间四个圆圈中的数加两遍，可得： 体填法如右上图。   【答案】26 【例 9】如图，大、中、小三个正方形组成了 8 个三角形，现在把 2、4、6、8 四个数分别填在大正方形的四个顶点；再把 2、4、6、8 分别填在中正方形的四个顶点上；最后把 2、4、6、8 分别填在小正方形的四个顶点上．⑴能不能使 8 个三角形顶点上数字之和都相等？⑵能不能使 8 个三角形顶点上数字之和各不相同？如果能，请画图填上满足要求的数；如果不能，请说明理由． 2 6 8 8 6 4 8 2 4 4 2 6 【考点】封闭型数阵图【难度】4 星【题型】填空【解析】⑴不能．如果这 8 个三角形顶点上数字之和都相等，设它们都等于 S ．【解析】 4 S  考察外面的 4 个三角形，每个三角形顶点上的数的和是 S ，在它们的和 4S 中，大正方形的 2、4、6、 8 各出现一次，中正方形的 2、4、6、8 各出现二次，即   ，但是三角形每个顶点上的数都是偶数，和不可能是奇数 15，因此这 8 个三角形顶点上的数字之和不可能都相等．    ，可能为 6、8、 ⑵由于三角形 3 个顶点上的数字之和最小为 2 2 2 6 10、……22、24，共有 10 个可能的值，而三角形只有 8 个，所以是有可能做到 8 个三角形的顶点上数字之和互不相同的．根据对称性，不妨舍去这 10 个可能值的首尾两个，把剩下 8 个值(8、10、12、14、16、18、20、22) 作为 8 个三角形的顶点上数字之和进行尝试，可以得到满足条件的填法，右上图就是一种填法．    ，最大为 8 8 8 24   ．得到 60 4 15 2 4 6 8    3 60 S    2 6 8 8 6 4 8 2 4 4 2 6 【答案】【例 10】将 1～16 分别填入下图（1）中圆圈内，要求每个扇形上四个数之和及中间正方形的四个数之和都为 34，图中已填好八个数，请将其余的数填完. 5-1-3-1.数阵图.题库教师版 page 5 of 11

【考点】封闭型数阵图【难度】4 星【题型】填空【解析】为了叙述方便，将圆圈内先填上字母，如图（2）所示：【解析】 9+15+a+c=34，5+10+e+g=34，7+14+b+d=34，11+8+f+h=34，c+d+e+f=34，化简得：a+c=10 4+6=10. e+g=19 3+16=19，6+13=19 b+d=13 1+12=13， f+h=15 2+13=15，3+12=15. a，b，c，d，e，f，g，h 应分别从 1，2，3，4，6，12，13，16 中选取.因为 a+c=10，所以只能选 a+c=4+6； b+d=13，只能选 b+d=13；e+g=19，只能选 e+g=3+16；f+h=15，只能选 f+h=2+13 若 d=1，c=4，则 e+f=34-1-4=29，有 e=16，f=13. 若 d=1，c=6，则 e+f=34-1-6=27，那么 e、f 无值可取，使其和为 27. 若 d=12，c=4，则 e+f=34-12-4=18，有 e=16，f=2. 若 d=12，c=6，则 e+f=34-12-6=16，有 e=3，f=13. 解：共有三个解（见图）. 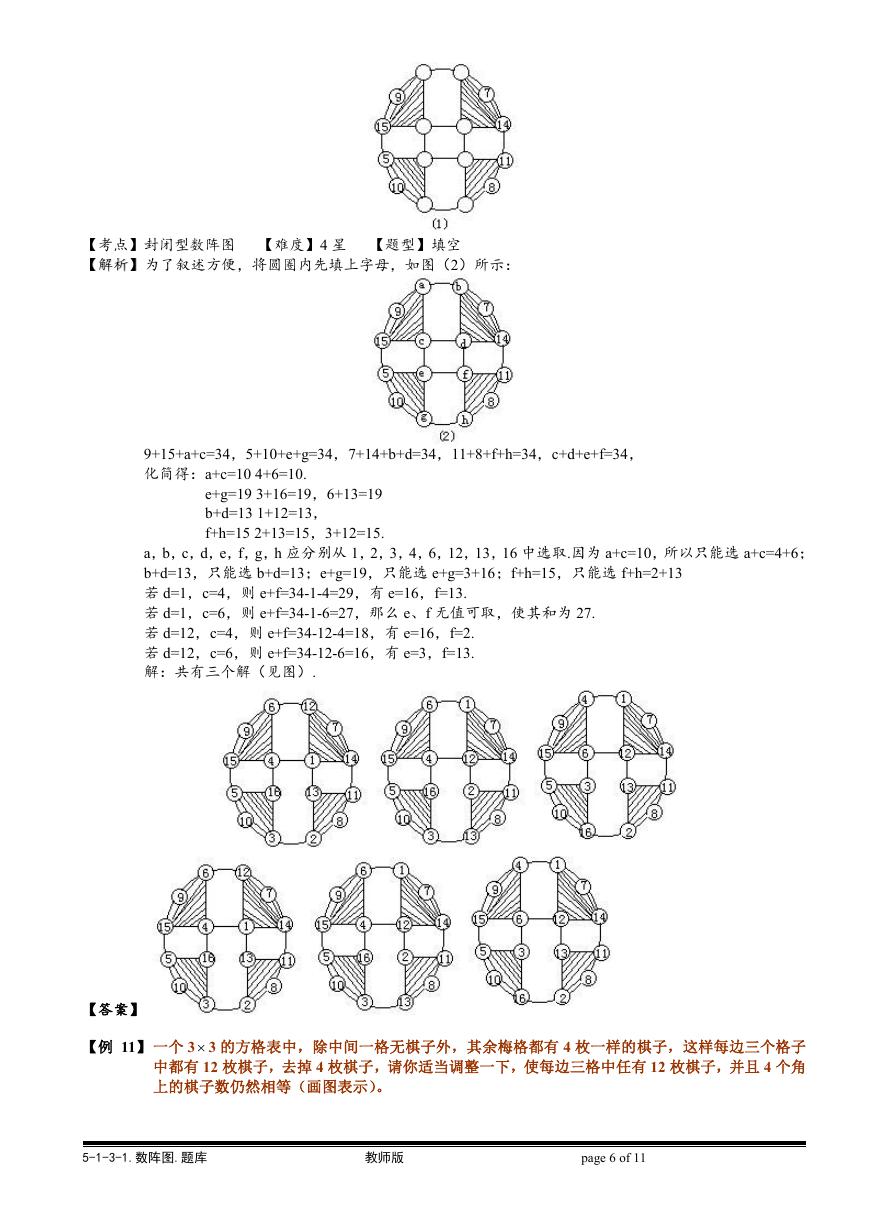【答案】【例 11】一个 3 3 的方格表中，除中间一格无棋子外，其余梅格都有 4 枚一样的棋子，这样每边三个格子中都有 12 枚棋子，去掉 4 枚棋子，请你适当调整一下，使每边三格中任有 12 枚棋子，并且 4 个角上的棋子数仍然相等（画图表示）。 5-1-3-1.数阵图.题库教师版 page 6 of 11

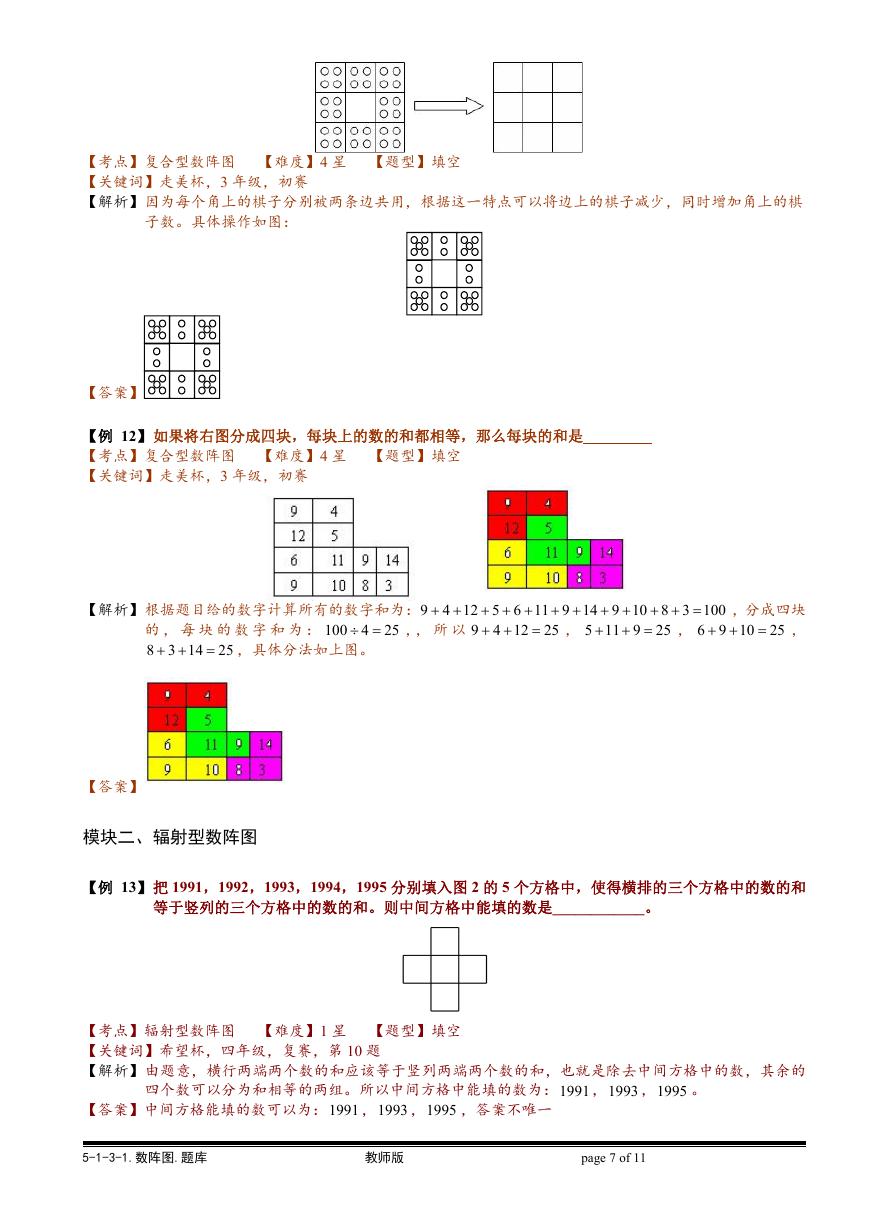
【考点】复合型数阵图【难度】4 星【题型】填空【关键词】走美杯，3 年级，初赛【解析】因为每个角上的棋子分别被两条边共用，根据这一特点可以将边上的棋子减少，同时增加角上的棋子数。具体操作如图：【答案】【例 12】如果将右图分成四块，每块上的数的和都相等，那么每块的和是【考点】复合型数阵图【难度】4 星【题型】填空【关键词】走美杯，3 年级，初赛【解析】根据题目给的数字计算所有的数字和为：9 4 12 5 6 11 9 14 9 10 8 3 100        ，，所以 9 4 12   25 的，每块的数字和为： 100 4 8 3 14  ，具体分法如上图。   25    ， 5 11 9    25    ，分成四块 25  ，   ， 6 9 10   25 【答案】模块二、辐射型数阵图【例 13】把 1991，1992，1993，1994，1995 分别填入图 2 的 5 个方格中，使得横排的三个方格中的数的和等于竖列的三个方格中的数的和。则中间方格中能填的数是____________。【考点】辐射型数阵图【难度】1 星【题型】填空【关键词】希望杯，四年级，复赛，第 10 题【解析】由题意，横行两端两个数的和应该等于竖列两端两个数的和，也就是除去中间方格中的数，其余的四个数可以分为和相等的两组。所以中间方格中能填的数为：1991 ，1993 ，1995 。【答案】中间方格能填的数可以为：1991 ，1993 ，1995 ，答案不唯一 5-1-3-1.数阵图.题库教师版 page 7 of 11

【例 14】请你把 1～7 这七个自然数，分别填在下图（1）的圆圈内，使每条直线上的三个数的和都相等.应怎样填？【考点】辐射型数阵图【难度】2 星【题型】填空【解析】为叙述方便，先在圆圈中标上字母，如下图（2），【解析】设 a+b+e=a+c+f=a+d+g=k，则（a+b+e）+（a+c+f）+（a+d+g）=3k 3a+b+c+d+e+f+g=3k 2a+（a+b+c+d+e+f+g）=3k 2a+（1+2+3+4+5+6+7）=3k 2a+28=3k a 为 1、4 或 7，若 a=1，则 k=10，直线上另外两个数的和为 9.在 2、3、4、5、6、7 中，2+7=3+6=4+5=9，因此得到一个解为：a=1，b=2，c=3，d=4，e=7，f=6，g=5. 若 a=4，则 k=12，直线上另外两个数的和为 8.在 1、2、3、5、6、7 中，1+7=2+6=3+5=8，因此得到第二个解为：a=4，b=1，c=2，d=3，e=7，f=6，g=5. 若 a=7，则 k=14，直线上另外两个数的和为 7.在 1、2、3、4、5、6 中，1+6=2+5=3+4=7，因此得到第三个解为：a=7，b=1， c=2，d=3，e=6，f=5，g=4. 解：共得到三个解：如下图. 例 2 为辐射型数阵图，填辐射型数阵图的关键在于确定中心数 a 和每条直线上几个圆圈内数的和 k. 【答案】【例 15】右边的一排方格中，除 9 、8 外，每个方格中的字都表示一个数(不同的字可以表示相同的数)，已知其中任何 3 个连续方格中的数相加起来都为 22 ，则“走”+“进”+“数”+“学”+“花”+“园” = 【考点】复合型数阵图【难度】2 星【题型】填空【关键词】走美杯，3 年级，初赛【解析】“走”+“进” 9   22 9  “数”+“学” 22 “花” 8  “园” 22 所以“走”+“进”+“数”+“学”+“花”+“园”  22 9 22 9 22 8      【答案】 40 40 【例 16】请在下图中每个方格中填一个数，使横行任意三个相邻方格内的数字之和都是 15，竖列任意三个相邻方格内的数字之和都是 18． 5-1-3-1.数阵图.题库教师版 page 8 of 11

分享到：

赞收藏

资料库

5-1-3-1 数阵图（一）.教师版.doc

相关推荐

小学奥数

热门标签

最新资料