4-4-1 圆与扇形（一）.教师版.doc-资料库

第1页 / 共13页

第2页 / 共13页

第3页 / 共13页

第4页 / 共13页

第5页 / 共13页

第6页 / 共13页

第7页 / 共13页

第8页 / 共13页

圆与扇形例题精讲研究圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形，通过变动图形的位置或对图形进行分割、旋转、拼补，使它变成可以计算出面积的规则图形来计算它们的面积．圆的面积 2πr ；扇形的面积 2π r  圆的周长 2πr  ；扇形的弧长 2π  r n 360 n  360 ；．一、跟曲线有关的图形元素： ①扇形：扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形，扇形是圆的一部分．我们经常说的 1 2 圆等等其实都是扇形，而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几圆、 1 4 圆、 1 6 n ． 360 比如：扇形的面积  所在圆的面积分之几．那么一般的求法是什么呢？关键是 n ； 360 n 360 2 半径(易错点是把扇形的周长等同于扇形的弧长) 扇形中的弧长部分  所在圆的周长 n 360 扇形的周长  所在圆的周长  ②弓形：弓形一般不要求周长，主要求面积．一般来说，弓形面积  扇形面积-三角形面积．(除了半圆) ③”弯角”：如图：弯角的面积  正方形-扇形 ④”谷子”：如图： “谷子”的面积  弓形面积 2 二、常用的思想方法： ①转化思想(复杂转化为简单，不熟悉的转化为熟悉的) ②等积变形(割补、平移、旋转等) ③借来还去(加减法) ④外围入手(从会求的图形或者能求的图形入手，看与要求的部分之间的”关系”) 板块一平移、旋转、割补、对称在曲线型面积中的应用【例 1】如图，圆 O 的直径 AB 与 CD 互相垂直，AB=10 厘米，以 C 为圆心，CA 为半径画弧。求月牙形 ADBEA（阴影部分）的面积。

【难度】3 星【考点】圆与扇形【关键词】华杯赛，决赛，第 9 题，10 分【解析】①月牙形 ADBEA(阴影部分)的面积＝半圆的面积+△ABC 的面积－扇形 CAEBC 的面积②月牙形  （平方厘米）,所以月牙形 ADBEA 的面积是 25 平方 ADBEA 的面积＝【题型】解答    π 5   π 50 25 25 1 2 2  1 4 厘米。【答案】25 【例 2】三个半径为 100 厘米且圆心角为 60º的扇形如图摆放；那么，这个封闭图形的周长是________厘米．（π取 3.14）【考点】圆与扇形【关键词】迎春杯，六年级，初赛，4 题【解析】三个扇形的弧长相当于半径 100 厘米，圆心角为 1800 的扇形的弧长，【题型】填空【难度】3 星【答案】314 2 3.14   180 360  厘米； 314 【例 3】分别以一个边长为 2 厘米的等边三角形的三个顶点为圆心，以 2 厘米为半径画弧，得到右图；那么，阴影图形的周长是_______厘米．(取 3.14) 【难度】3 星【考点】圆与扇形【关键词】迎春杯，六年级，初赛，试题【解析】每段弧长为 1 6 【答案】12.56 C圆，所以 C 阴影 16   6 【题型】填空 C 圆 C 圆 C 阴影=6× 1 6 C 圆= C 圆，所以 C 阴影 12.56 【例 4】下图中每一个小正方形的面积是 1 平方厘米，那么格线部分的面积是多少平方厘米？【考点】圆与扇形【解析】割补法．如右图，格线部分的面积是 36 平方厘米．【答案】36 【难度】3 星【题型】解答

【巩固】下图中每一个小正方形的面积是 1 平方厘米，那么格线部分的面积是多少平方厘米？【考点】圆与扇形【解析】割补法．如右图，格线部分的面积是 36 平方厘米．【答案】36 【难度】3 星【题型】解答【例 5】如图，在 18 8 的方格纸上，画有 1，9，9，8 四个数字．那么，图中的阴影面积占整个方格纸面积的几分之几？【考点】圆与扇形【难度】3 星【题型】解答【解析】我们数出阴影部分中完整的小正方形有 8+15+15+16  54 个，其中部分有 6+6+8  20 个，部分有 6+6+8  20(个)，而 1 个正好组成一个完整的小正方形，所以阴影部分共包含 54+20  74(个)完整小正方形，而整个方格纸包含 8  18  144(个)完整小正方形．所以图中阴影面积占整个方格纸面积的 74 144 ，即 37 72 和 1 个．【答案】 37 72 【巩固】在 4×7 的方格纸板上面有如阴影所示的”6”字，阴影边缘是线段或圆弧．问阴影面积占纸板面积的几分之几？【考点】圆与扇形【难度】3 星【解析】矩形纸板共 28 个小正方格，其中弧线都是【题型】解答 1 4 圆周，非阴影部分有 3 个完整的小正方形，其余部分可拼成 6 个小正方格．因此阴影部分共 28－6－3=19 个小正方格．所以，阴影面积占纸板面积的 19 28 ．

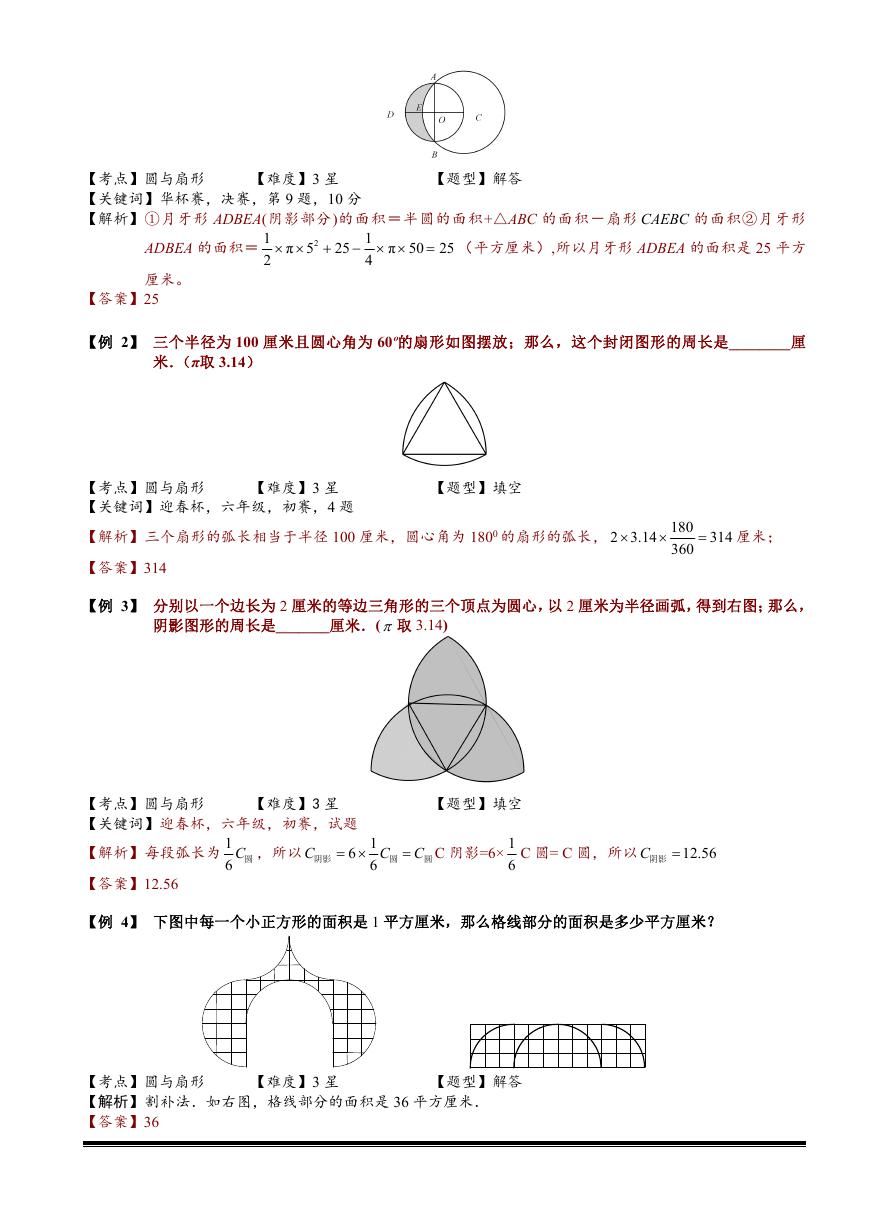
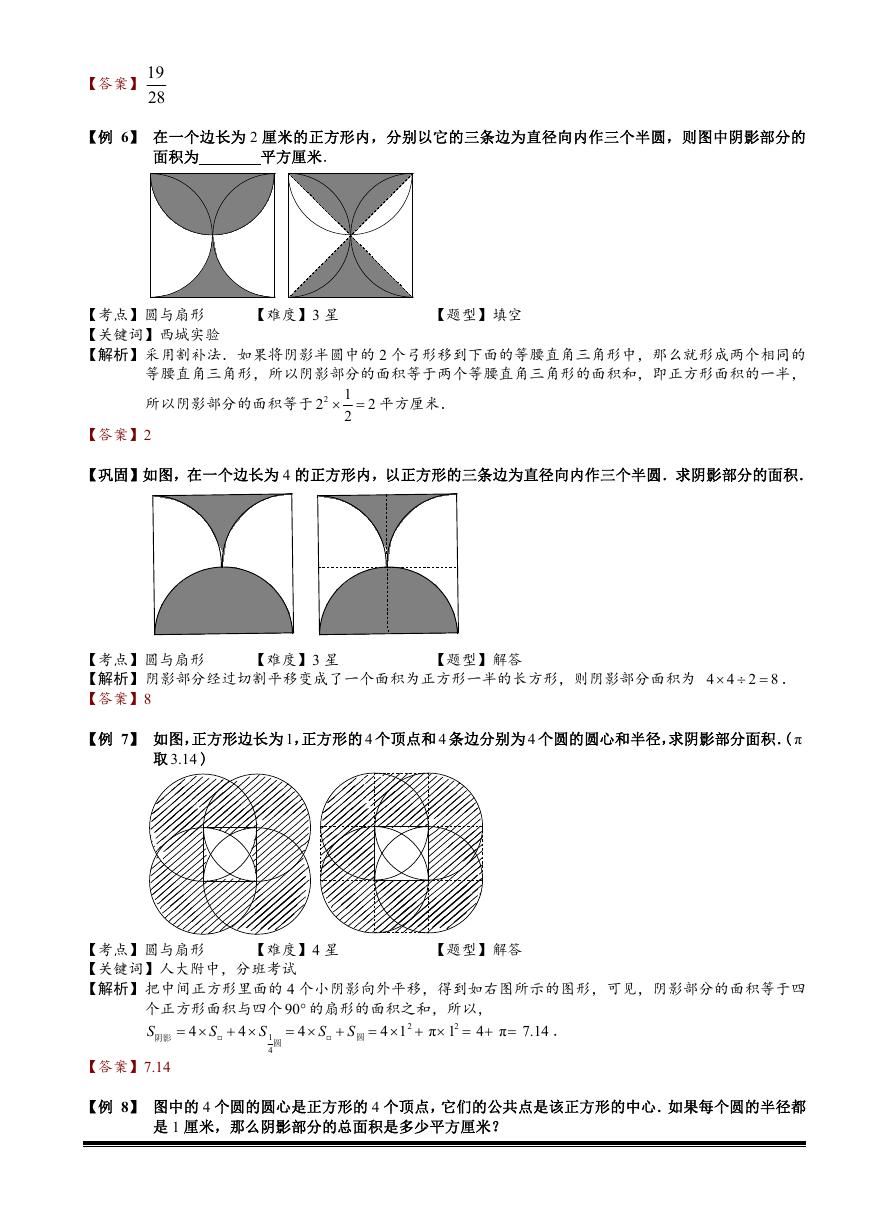
【答案】 19 28 【例 6】在一个边长为 2 厘米的正方形内，分别以它的三条边为直径向内作三个半圆，则图中阴影部分的面积为平方厘米．【难度】3 星【考点】圆与扇形【关键词】西城实验【解析】采用割补法．如果将阴影半圆中的 2 个弓形移到下面的等腰直角三角形中，那么就形成两个相同的等腰直角三角形，所以阴影部分的面积等于两个等腰直角三角形的面积和，即正方形面积的一半，【题型】填空所以阴影部分的面积等于 2 2 【答案】2   平方厘米． 2 1 2 【巩固】如图，在一个边长为 4 的正方形内，以正方形的三条边为直径向内作三个半圆．求阴影部分的面积．【考点】圆与扇形【解析】阴影部分经过切割平移变成了一个面积为正方形一半的长方形，则阴影部分面积为 4 4 2 8 【答案】8 【题型】解答    ．【难度】3 星【例 7】如图，正方形边长为 1，正方形的 4 个顶点和 4 条边分别为 4 个圆的圆心和半径，求阴影部分面积．( π 取 3.14 ) 【考点】圆与扇形【关键词】人大附中，分班考试【解析】把中间正方形里面的 4 个小阴影向外平移，得到如右图所示的图形，可见，阴影部分的面积等于四【题型】解答【难度】4 星个正方形面积与四个 90 的扇形的面积之和，所以， S 4 1   2 π 1 4   4   S 4   S    S 2 阴影圆 S   1 4 圆 4 π    7.14 ．【答案】7.14 【例 8】图中的 4 个圆的圆心是正方形的 4 个顶点，它们的公共点是该正方形的中心．如果每个圆的半径都是 1 厘米，那么阴影部分的总面积是多少平方厘米？

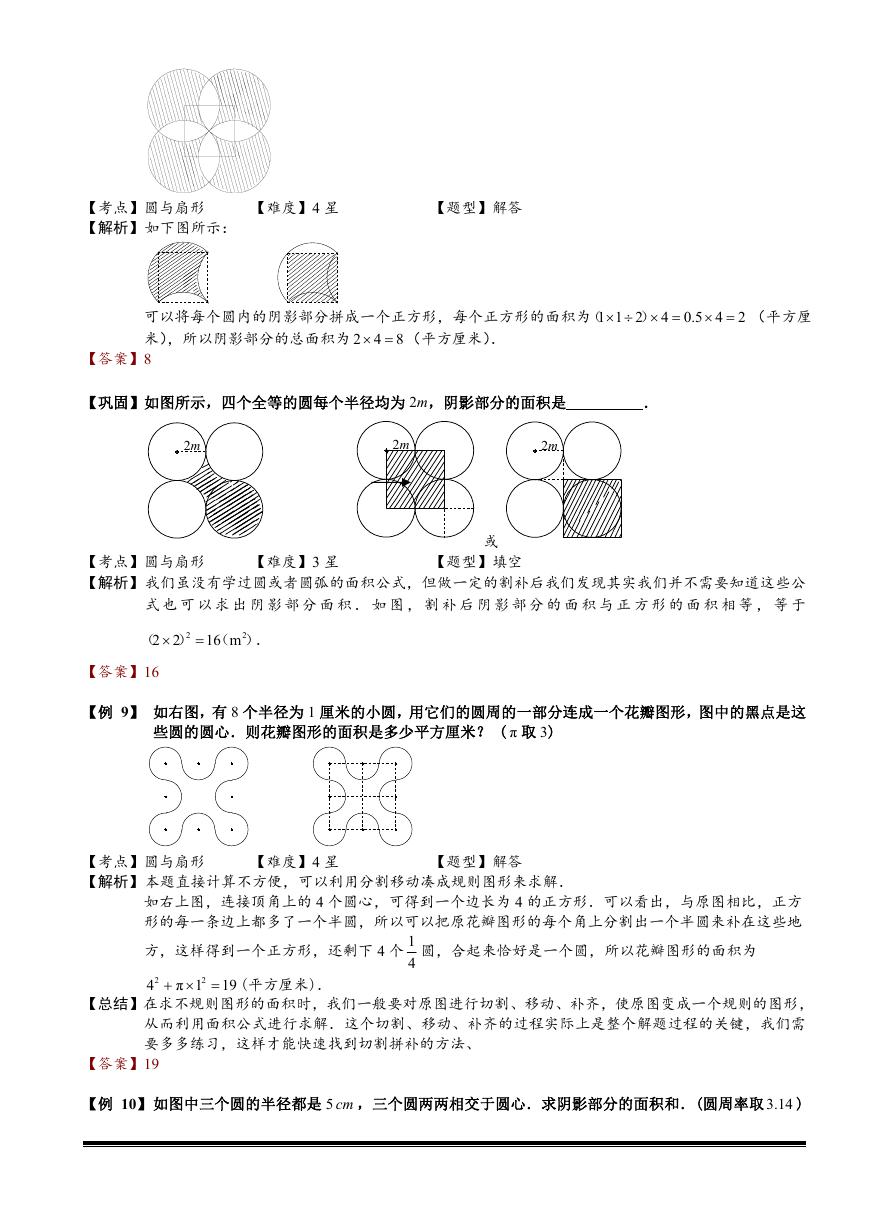
【考点】圆与扇形【解析】如下图所示：【难度】4 星【题型】解答可以将每个圆内的阴影部分拼成一个正方形，每个正方形的面积为 1 1 2 米），所以阴影部分的总面积为 2 4 8   （平方厘米）．   （）   4 0.5 4   2 （平方厘【答案】8 【巩固】如图所示，四个全等的圆每个半径均为 2m，阴影部分的面积是． 2 m 2 m 2 m 或【考点】圆与扇形【解析】我们虽没有学过圆或者圆弧的面积公式，但做一定的割补后我们发现其实我们并不需要知道这些公式也可以求出阴影部分面积．如图，割补后阴影部分的面积与正方形的面积相等，等于【题型】填空【难度】3 星（）（）． 16 m 2 2   2 2 【答案】16 【例 9】如右图，有 8 个半径为 1 厘米的小圆，用它们的圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心．则花瓣图形的面积是多少平方厘米？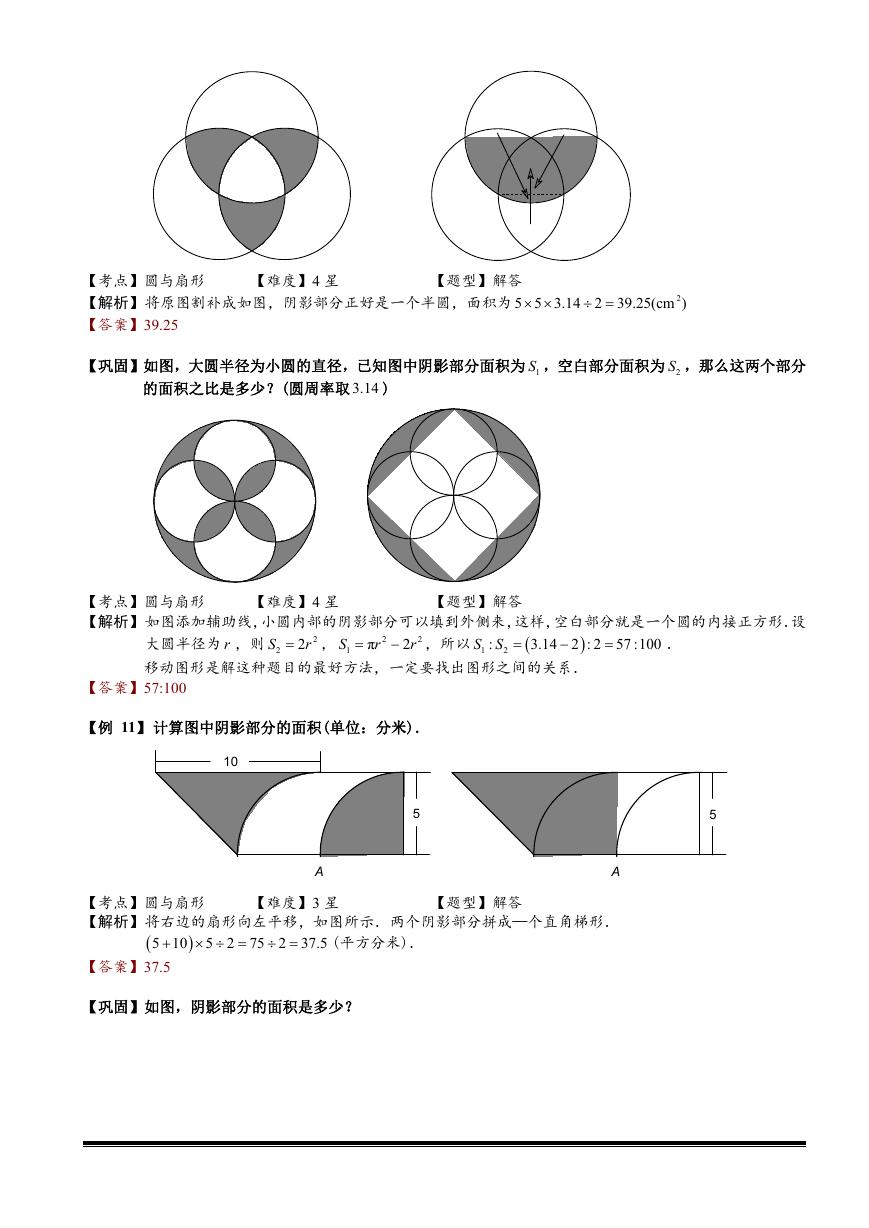 ( π 取 3) 【考点】圆与扇形【解析】本题直接计算不方便，可以利用分割移动凑成规则图形来求解．【题型】解答【难度】4 星如右上图，连接顶角上的 4 个圆心，可得到一个边长为 4 的正方形．可以看出，与原图相比，正方形的每一条边上都多了一个半圆，所以可以把原花瓣图形的每个角上分割出一个半圆来补在这些地方，这样得到一个正方形，还剩下 4 个 1 4 4 圆，合起来恰好是一个圆，所以花瓣图形的面积为 (平方厘米)． 2 π 1   19  2 【总结】在求不规则图形的面积时，我们一般要对原图进行切割、移动、补齐，使原图变成一个规则的图形，从而利用面积公式进行求解．这个切割、移动、补齐的过程实际上是整个解题过程的关键，我们需要多多练习，这样才能快速找到切割拼补的方法、【答案】19 【例 10】如图中三个圆的半径都是 5 cm ，三个圆两两相交于圆心．求阴影部分的面积和．(圆周率取 3.14 )

【考点】圆与扇形【解析】将原图割补成如图，阴影部分正好是一个半圆，面积为【答案】39.25 【题型】解答【难度】4 星 2 5 5 3.14 2 39.25(cm )     【巩固】如图，大圆半径为小圆的直径，已知图中阴影部分面积为 1S ，空白部分面积为 2S ，那么这两个部分的面积之比是多少？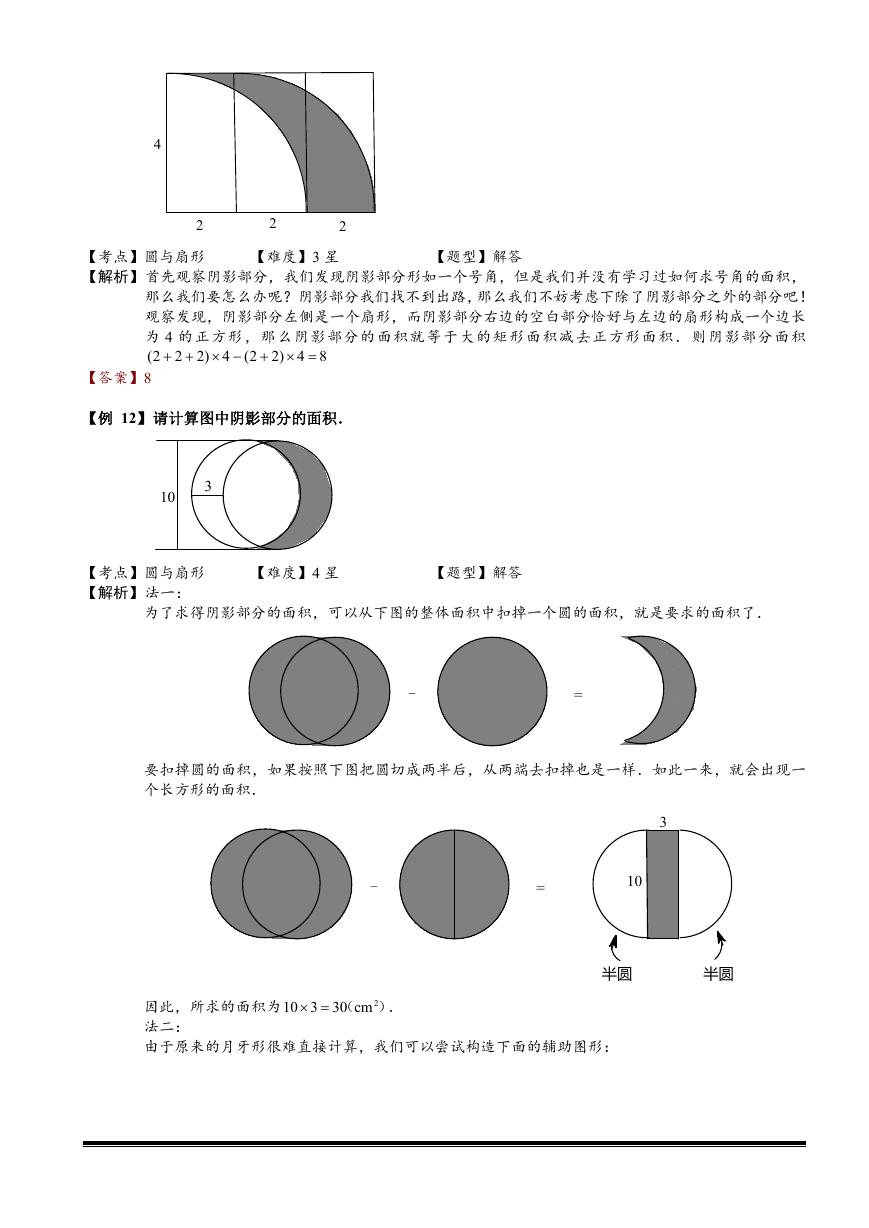(圆周率取 3.14 ) 【考点】圆与扇形【解析】如图添加辅助线，小圆内部的阴影部分可以填到外侧来，这样，空白部分就是一个圆的内接正方形．设【题型】解答【难度】4 星 2 r 2  大圆半径为 r ，则移动图形是解这种题目的最好方法，一定要找出图形之间的关系．  ，所以 S S  1 r ， π r S 1 2   S 2 : 2 2 2 3.14 2 : 2 57 :100   ．【答案】57:100 【例 11】计算图中阴影部分的面积(单位：分米)． 10 5 5 A A 【考点】圆与扇形【解析】将右边的扇形向左平移，如图所示．两个阴影部分拼成—个直角梯形．【题型】解答【难度】3 星  5 10  【答案】37.5     5 2 75 2 37.5   (平方分米)．【巩固】如图，阴影部分的面积是多少？

4 2 2 2 【难度】3 星【考点】圆与扇形【解析】首先观察阴影部分，我们发现阴影部分形如一个号角，但是我们并没有学习过如何求号角的面积，那么我们要怎么办呢？阴影部分我们找不到出路，那么我们不妨考虑下除了阴影部分之外的部分吧！观察发现，阴影部分左侧是一个扇形，而阴影部分右边的空白部分恰好与左边的扇形构成一个边长为 4 的正方形，那么阴影部分的面积就等于大的矩形面积减去正方形面积．则阴影部分面积 (2 2 2) 4 (2 2) 4 8 【题型】解答        【答案】8 【例 12】请计算图中阴影部分的面积． 3 10 【考点】圆与扇形【解析】法一：【难度】4 星【题型】解答为了求得阴影部分的面积，可以从下图的整体面积中扣掉一个圆的面积，就是要求的面积了． - = 要扣掉圆的面积，如果按照下图把圆切成两半后，从两端去扣掉也是一样．如此一来，就会出现一个长方形的面积． 3 - = 10 半圆半圆因此，所求的面积为法二：由于原来的月牙形很难直接计算，我们可以尝试构造下面的辅助图形： 10 3 30 cm   （）． 2

3cm 3cm 10cm 10cm 辅助图形缩进的部分超出的部分 3cm 如左上图所示，我们也可以这样来思考，让图形往右侧平移 3cm 就会得到右上图中的组合图形，而这个组合图形中右端的月牙形正是我们要求的面积．显然图中右侧延伸出了多少面积，左侧就会缩进多少面积．因此，所求的面积是   （）． 10 3 30 cm 2 【答案】30 【例 13】求图中阴影部分的面积． A 12 D A 12 D B 12 C B 12 C 【难度】3 星【考点】圆与扇形【解析】如图，连接 BD ，可知阴影部分的面积与三角形 BCD 的面积相等，即为 1 1 12 12 36 【答案】36 【题型】解答 2 2     ．【例 14】求如图中阴影部分的面积．(圆周率取 3.14 ) 4 4 【考点】圆与扇形【解析】可将左下橄榄型的阴影部分剖开，两部分分别顺逆时针 90 ，则阴影部分转化为四分之一圆减去一【题型】解答【难度】2 星 1 4 1 2   π 4 2     4 4 4.56 ．个等腰直角三角形，所以阴影部分的面积为【答案】4.56 【巩固】如图，四分之一大圆的半径为 7，求阴影部分的面积，其中圆周率 π 取近似值 22 7 ．【考点】圆与扇形【难度】3 星【题型】解答

资料库

4-4-1 圆与扇形（一）.教师版.doc

相关推荐

小学奥数

热门标签

最新资料