第四讲配对求和.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：0.06M 资料格式：doc 举报版权申诉

第1页 / 共5页

第2页 / 共5页

第3页 / 共5页

第4页 / 共5页

第5页 / 共5页

文本预览

第四讲配对求和（简单整数数列的计算）知识要点：配对技巧项数的确定小朋友们，你听过德国著名数学家、物理学家和天文学家高斯的故事吗？他从小就聪颖过人，还在他8岁的时候，老师给班上同学出了一道题：1＋2＋3＋4＋……＋99＋100＝？8岁的高斯很快报出了得数：5050。这个答案完全正确！最让老师吃惊的是，小高斯计算的速度如此快捷！那么，小高斯是用什么办法算得这么快的呢？原来，根据所给算式的特点，他用了一种巧妙的方法——配对求和。采用这种方法，很多整数数列求和的问题都能迎刃而解了。典型例题例【1】计算：1＋2＋3＋4＋5＋6＋7＋8＋9＋10 分析 1 在这个算式中，共有 10 个数，将和为 11 的两个数一一配对，可配成 5 对。 1 2 3 4 5 6 7 8 9 10

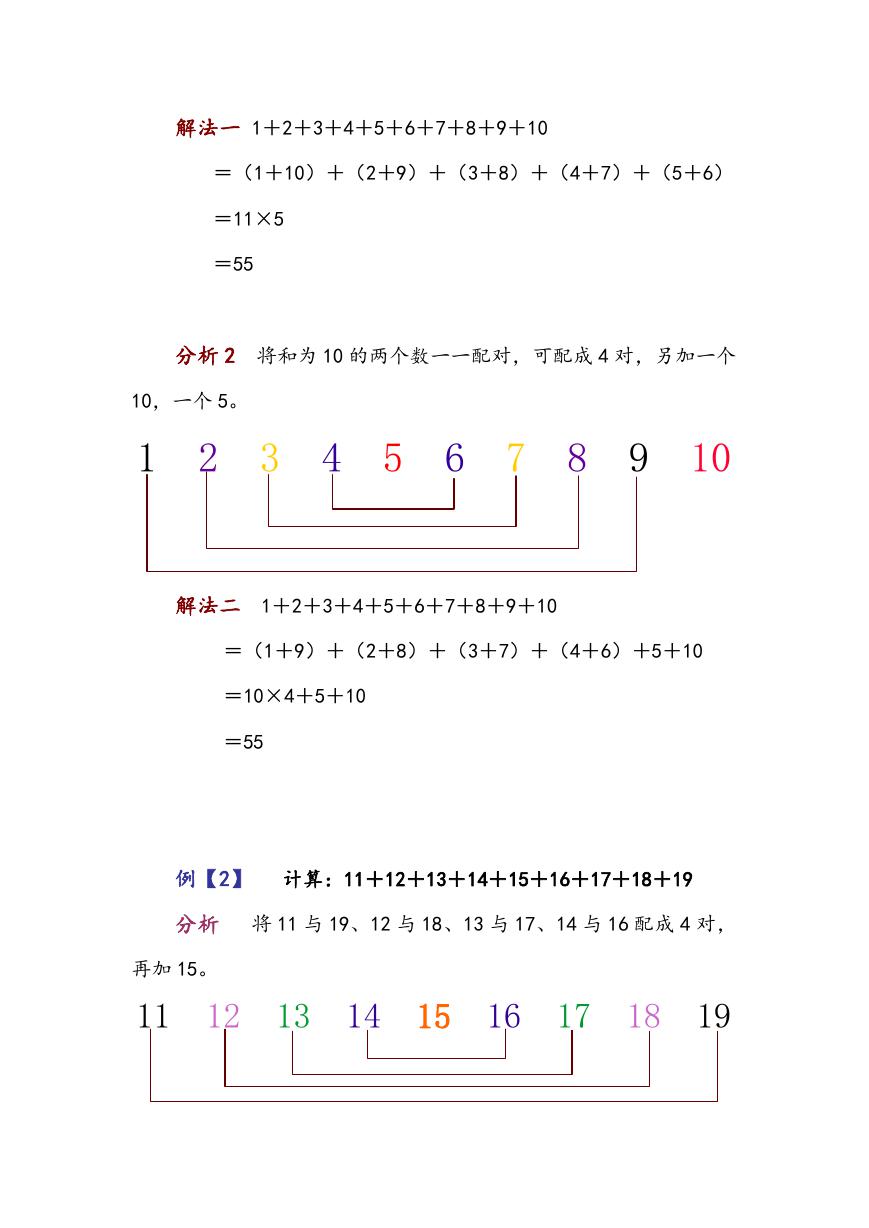
解法一 1＋2＋3＋4＋5＋6＋7＋8＋9＋10 ＝（1＋10）＋（2＋9）＋（3＋8）＋（4＋7）＋（5＋6）＝11×5 ＝55 分析 2 将和为 10 的两个数一一配对，可配成 4 对，另加一个 10，一个 5。 1 2 3 4 5 6 7 8 9 10 解法二 1＋2＋3＋4＋5＋6＋7＋8＋9＋10 ＝（1＋9）＋（2＋8）＋（3＋7）＋（4＋6）＋5＋10 ＝10×4＋5＋10 ＝55 例【2】计算：11＋12＋13＋14＋15＋16＋17＋18＋19 分析将 11 与 19、12 与 18、13 与 17、14 与 16 配成 4 对，再加 15。 11 12 13 14 15 16 17 18 19

解 11＋12＋13＋14＋15＋16＋17＋18＋19 ＝（11＋19）＋（12＋18）＋（13＋17）＋（14＋16）＋15 ＝30×4＋15 ＝135 例【3】计算：101＋102＋103＋104＋105＋106＋107＋108 ＋109＋110 分析此题中每个数里都包含了一个 100，可以把这 10 个 100 分离出来，转化为例【1】解 101＋102＋103＋104＋105＋106＋107＋108＋109＋110 ＝100×10＋（1＋2＋3＋4＋5＋6＋7＋8＋9＋10）＝1000＋11×5 ＝1055 例【4】计算 500－（11＋13＋15＋17＋19＋21＋23＋25＋ 27＋29）分析先用配对的方法计算 11＋13＋15＋17＋19＋21＋23＋ 25＋27＋29

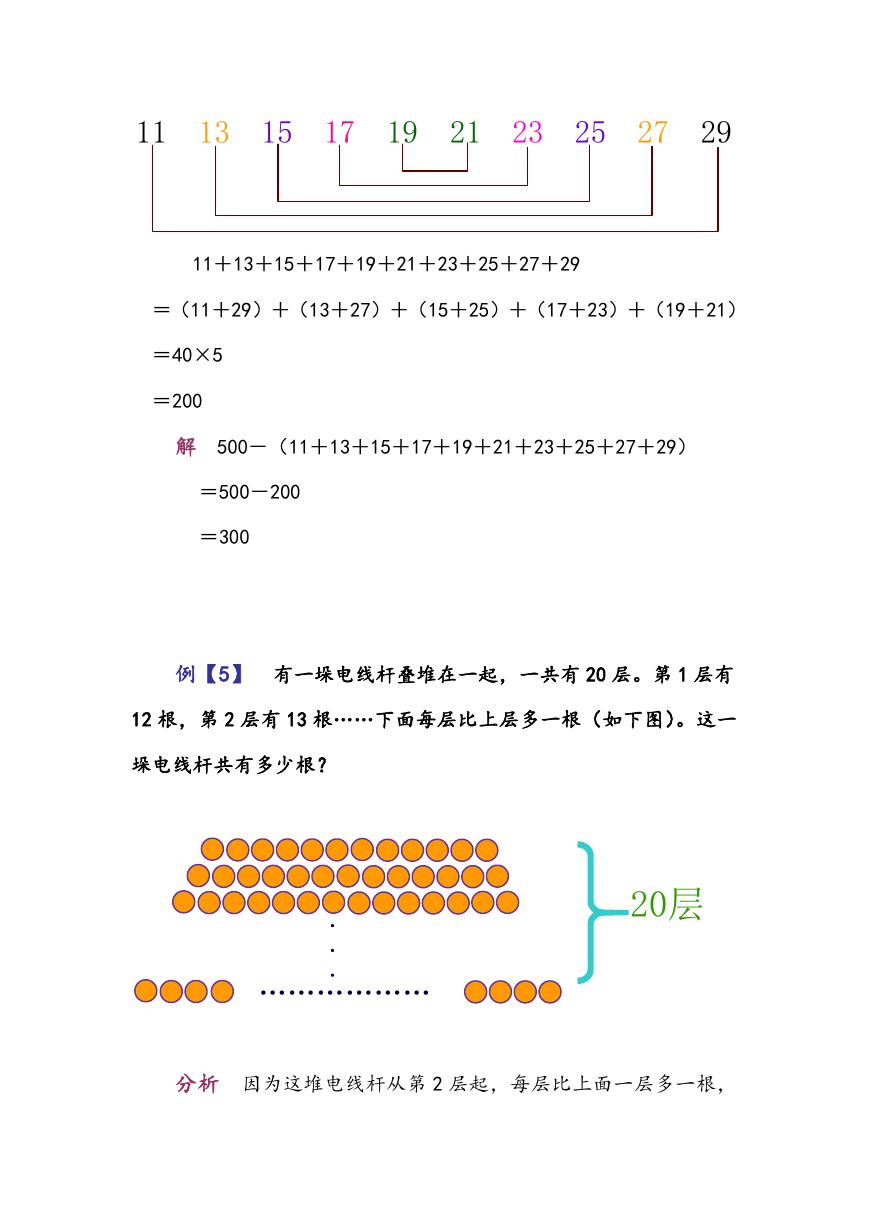
11 13 15 17 19 21 23 25 27 29 11＋13＋15＋17＋19＋21＋23＋25＋27＋29 ＝（11＋29）＋（13＋27）＋（15＋25）＋（17＋23）＋（19＋21）＝40×5 ＝200 解 500－（11＋13＋15＋17＋19＋21＋23＋25＋27＋29）＝500－200 ＝300 例【5】有一垛电线杆叠堆在一起，一共有 20 层。第 1 层有 12 根，第 2 层有 13 根……下面每层比上层多一根（如下图）。这一垛电线杆共有多少根？ . . . ……………… 20层分析因为这堆电线杆从第 2 层起，每层比上面一层多一根，

共有 20 层，所以，这垛电线杆的总数为： 12＋13＋14＋……＋29＋30＋31 ＝（12＋31）×20÷2 ＝43×20÷2 ＝430 （注：20÷2 表示一共配成的对数，即和数为 43 的有 20÷2 对）小结用配对方法求和，实质上是变加法（连加）为乘法。要正确、合理地运用这种方法，首先必须弄清应当怎样把一串数进行合理的配对。有时，一串数的个数不是双数，就不能刚好配对，还留下一个数，要弄清这个数是几；有时，一串数虽然个数是双数，但为了计算简便，往往把其中两个或者几个数放在一旁，将其余数配对，使每对中两数的和恰好是整十或整百数。

分享到：

赞收藏

资料库

第四讲配对求和.doc

相关推荐

小学奥数

热门标签

最新资料