4-1-3 角度计算.教师版.doc-资料库

第1页 / 共5页

第2页 / 共5页

第3页 / 共5页

第4页 / 共5页

第5页 / 共5页

4-1-3.角度计算知识点拨一、角 1、角的定义：自一点引两条射线所成的图形叫角 2、表示角的符号：∠ 3、角的分类：锐角、直角、钝角、平角、周角、负角、正角、优角、劣角、0 角这 10 种（1）锐角：大于 0°，小于 90°的角叫做锐角。（2）直角：等于 90°的角叫做直角。（3）钝角：大于 90°而小于 180°的角叫做钝角。（4）平角：等于 180°的角叫做平角。（5）优角：大于 180°小于 360°叫优角。（6）劣角：大于 0°小于 180°叫做劣角，锐角、直角、钝角都是劣角。（7）周角：等于 360°的角叫做周角。（8）负角：按照顺时针方向旋转而成的角叫做负角。（9）正角：逆时针旋转的角为正角。（10） 0 角：等于零度的角。 4、角的大小：角的大小与边的长短没有关系；角的大小决定于角的两条边张开的程度，张开的越大，角就越大，相反，张开的越小，角则越小。二、三角形 1、三角形的定义：由三条边首尾相接组成的封闭图形叫做三角形 2、内角和：三角形的内角和为 180 度；外角：（1）三角形的一个外角等于另外两个内角的和；（2）三角形的一个外角大于其他两内角的任一个角。 3、三角形的分类（1）按角分：锐角三角形：三个角都小于 90 度。直角三角形：有一个角等于 90 度。钝角三角形：有一个角大于 90 度。注：锐角三角形和钝角三角形可统称为斜三角形（2）按边分：不等腰三角形；等腰三角形（含等边三角形）。模块一、角度计算【例 1】有下列说法： (1)一个钝角减去一个直角，得到的角一定是锐角， (2)一个钝角减去一个锐姥，得到的角不可能还是钝角． (3)三角形的三个内麓中至多有一个钝角． (4)三角形的三个内角中至少有两个锐角． (5)三角形的三个内角可以都是锐角． (6)直角三角形中可胄邕有钝角． (7) 25 的角用 10 倍的放大镜看就变成了 250 其中，正确说法的个数是【考点】角度计算【难度】3 星【题型】填空【解析】几何问题(1)、(3)、(4)、(5)是正确的说法．【答案】(1)、(3)、(4)、(5)是正确的说法 4-1-3.角度计算题库 page 1 of 5

【例 2】下图是 3×3 的正方形方格，∠1 与∠2 相比，较大的是_____。【考点】角度计算【难度】2 星【题型】填空【解析】∠1 【答案】∠1 【例 3】如图，在直角 AOB 内有一条射线OC ，并且 AOC 比 BOC 大 20。则 BOC 是__________ 【考点】角度计算【难度】3 星【题型】填空【解析】  90 【答案】 35 2 35    20     【例 4】直线 AB、CD 相交，若∠1、∠2 和∠3 的关系如图所示。则∠3  ∠1=______ 。【考点】角度计算【难度】3 星【题型】填空【解析】∠1+∠2=90，∠2+∠3=180，所以（∠2+∠3）  （∠1+∠2）  ∠3  ∠1= 90 【答案】 90 【例 5】如图，共端点 A 的线段 a 与 d，b 与 e，c 与 f 分别垂直，a 与 b 的夹角是 30°，e 与 f 的夹角是 45°，求 c 与 d 的夹角的度数。【考点】角度计算【难度】3 星【题型】解答【解析】a 与 b 的夹角为 30 度，所以 b 与 d 的夹角为 90 30 60  以 c 与 d 的夹角为 90 30 45 15  度.    度，所以 d 与 e 的夹角是 90 60 30  度，所  【答案】15 度【例 6】如图，直角的顶点在直线 l 上，则图中所有小于平角的角之和是图 4 度。【考点】角度计算【难度】3 星【题型】填空【解析】由一部分组成的角之和是 180 度，由两部分组成的角之和是 180+90 度，一共 180+180+90=450 度。【答案】450 度 4-1-3.角度计算题库 page 2 of 5

【例 7】如图，∠AOB 的顶点 0 在直线 l 上，已知图中所有小于平角的角之和是 400 度，则∠AOB＝________ 度。【考点】角度计算【难度】3 星【题型】填空【解析】所有小于平角的角之和=∠1+∠2+∠3+∠1+∠2+∠2+∠3=400 度，又∠1+∠2+∠3=180 度，故∠2=40 度。【答案】∠AOB=40 度【例 8】两条直线相交，四个交角中的一个锐角或一个直角称为这两条直线的“夹角”（见下图）。如果在平面上画 L 条直线，要求它们两两相交，并且“夹角”只能是 15°、30°、45°、60°、75°、90°之一，问：（1）L 的最大值是多少？（2）当 L 取最大值时，问所有的“夹角”的和是多少？【考点】角度计算【难度】4 星【题型】解答【解析】（1）固定平面上一条直线,其它直线与此条固定直线的交角自这条固定直线起逆时针计算,只能是 15°、30°、45°、60°、75°、90°、105°、120°、135°、150°、165°十一种角度之一，所以，平面上最多有 12 条直线。否则，必有两条直线平行。（2）根据题意，相交后的直线会产生 15°、30°、45°、60°、75°的两条直线相交的情况均有 12 种；他们的角度和是（15+30+45+60+75）×12=2700°；产生 90°角的有第 1 和第 7 条直线；第 2 和第 8 条直线；第 3 和第 9 条直线；第 4 和第 10 条直线；第 5 和第 11 条直线；第 6 和第 12 条直线共 6 个，他们的角度和是 90×6=540°；所以所有夹角和是 2700+540=3240°。【答案】（1）12 条；（2）3240° 【例 9】如图，点 O 为直线 AB 上一点， BOC 是直角，  BOD COD  :  则 AOD 4:1 是______度. 【考点】角度计算【难度】3 星【题型】填空 COD 【解析】【答案】60 度 BOD COD BOC  ，所以 4:1   :   ，所以 3:1 COD  30  .所以 AOD 是 60 度.  : 模块二、三角形内的角度计算 4-1-3.角度计算题库 page 3 of 5

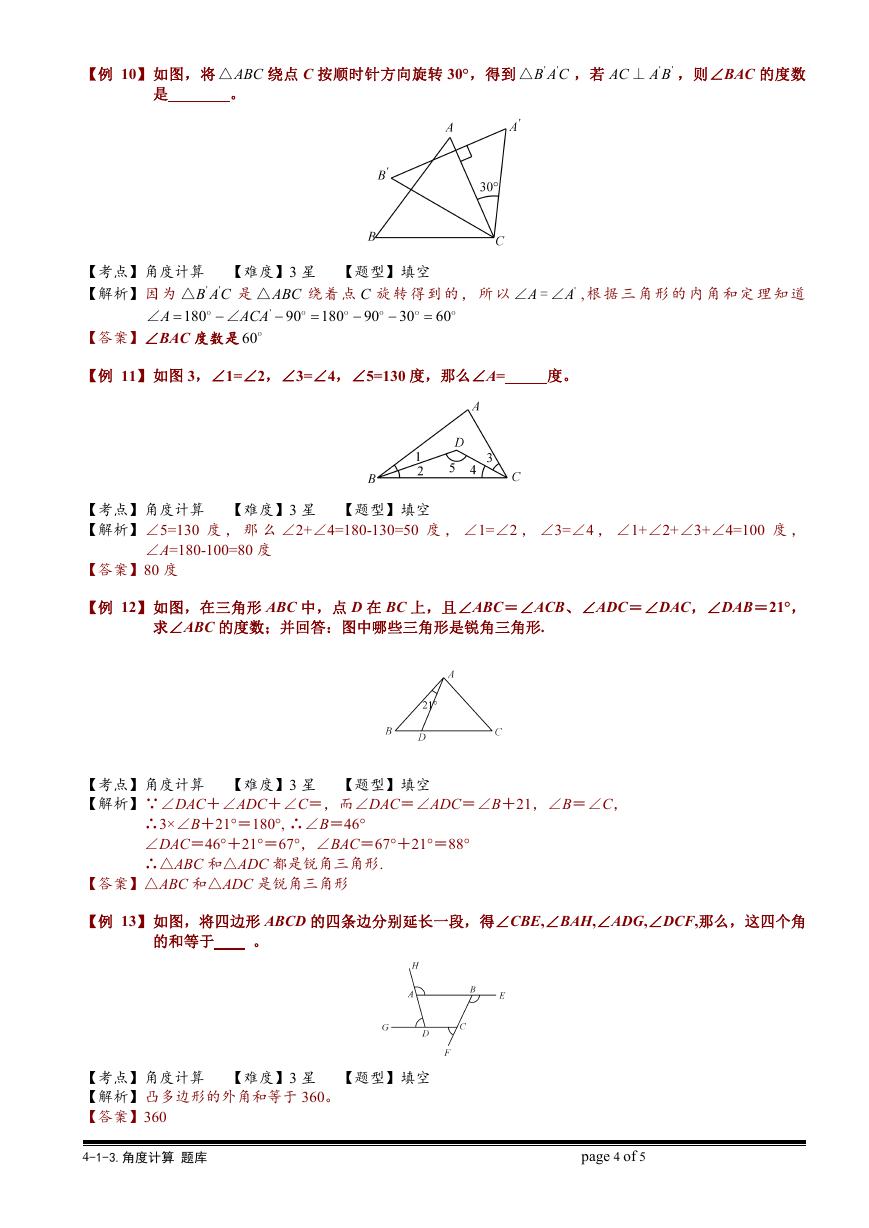
【例 10】如图，将 ABC△ 绕点 C 按顺时针方向旋转 30°，得到 ' 'B AC△ ，若 AC ' A B⊥ ' ，则∠BAC 的度数是。【考点】角度计算【难度】3 星【题型】填空 'B AC△ 【解析】因为 ' 180   ∠ 是 ABC△ 90 ACA 【答案】∠BAC 度数是 60o 30 90 绕着点 C 旋转得到的，所以  180 60  ∠ A o  o  o  o o ' o ∠ = ∠ , 根据三角形的内角和定理知道 ' A A 【例 11】如图 3，∠1=∠2，∠3=∠4，∠5=130 度，那么∠A= 度。【考点】角度计算【难度】3 星【题型】填空【解析】∠5=130 度，那么 ∠2+∠4=180-130=50 度， ∠1=∠2 ， ∠3=∠4 ， ∠1+∠2+∠3+∠4=100 度， ∠A=180-100=80 度【答案】80 度【例 12】如图，在三角形 ABC 中，点 D 在 BC 上，且∠ABC＝∠ACB、∠ADC＝∠DAC，∠DAB＝21°，求∠ABC 的度数；并回答：图中哪些三角形是锐角三角形. 【考点】角度计算【难度】3 星【题型】填空【解析】∵∠DAC＋∠ADC＋∠C＝，而∠DAC＝∠ADC＝∠B＋21，∠B＝∠C， ∴3×∠B＋21°＝180°, ∴∠B＝46° ∠DAC＝46°＋21°＝67°，∠BAC＝67°＋21°＝88° ∴△ABC 和△ADC 都是锐角三角形. 【答案】△ABC 和△ADC 是锐角三角形【例 13】如图，将四边形 ABCD 的四条边分别延长一段，得∠CBE,∠BAH,∠ADG,∠DCF,那么，这四个角的和等于。【考点】角度计算【难度】3 星【题型】填空【解析】凸多边形的外角和等于 360。【答案】360 4-1-3.角度计算题库 page 4 of 5

模块三、角度在行程问题中的应用【例 14】小明从家里出发，先向东偏北 30°的方向跑了 350 米到达点 A，接着向北偏西 30°的方向跑了 200 米到达点 B，然后又向西偏南 30°的方向跑了 350 米到达点 C，这时小明距离家米。【考点】角度计算【难度】2 星【题型】填空【解析】通过画图可知小明距离家是 200 米。【答案】200 米【例 15】小明从家出发，先向东偏北 30°的方向跑了 350 米到达点 A，接着向北偏西 30°的方向跑了 200 米到达点 B，然后又向西偏南 30°的方向跑了 350 米到达点 C，这时小明距家米。【考点】角度计算【难度】2 星【题型】填空【解析】200 米【答案】200 米 4-1-3.角度计算题库 page 5 of 5

资料库

4-1-3 角度计算.教师版.doc

相关推荐

小学奥数

热门标签

最新资料