7-2-3 乘法原理之染色法.教师版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：0.96M 资料格式：doc 举报版权申诉

第1页 / 共8页

第2页 / 共8页

第3页 / 共8页

第4页 / 共8页

第5页 / 共8页

第6页 / 共8页

第7页 / 共8页

第8页 / 共8页

文本预览

7-2-3 乘法原理之染色问题教学目标 1.使学生掌握乘法原理主要内容，掌握乘法原理运用的方法； 2.使学生分清楚什么时候用乘法原理，分清有几个必要的步骤，以及各步之间的关系． 3.培养学生准确分解步骤的解题能力；乘法原理的数学思想主旨在于分步考虑问题，本讲的目的也是为了培养学生分步考虑问题的习惯．知识要点一、乘法原理概念引入老师周六要去给同学们上课，首先得从家出发到长宁上 8 点的课，然后得赶到黄埔去上下午 1 点半的课．如果说申老师的家到长宁有 5 种可选择的交通工具（公交、地铁、出租车、自行车、步行），然后再从长宁到黄埔有 2 种可选择的交通工具（公交、地铁），同学们，你们说老师从家到黄埔一共有多少条路线？我们看上面这个示意图，老师必须先的到长宁，然后再到黄埔．这几个环节是必不可少的，老师是一定要先到长宁上完课，才能去黄埔的．在没学乘法原理之前，我们可以通过一条一条的数，把线路找出来，显而易见一共是 10 条路线．但是要是老师从家到长宁有 25 种可选择的交通工具，并且从长宁到黄埔也有 30 种可选择的交通工具，那一共有多少条线路呢？这样数，恐怕是要耗费很多的时间了．这个时候我们的乘法原理就派上上用场了．二、乘法原理的定义完成一件事，这个事情可以分成 n 个必不可少的步骤（比如说老师从家到黄埔，必须要先到长宁，那么一共可以分成两个必不可少的步骤，一是从家到长宁，二是从长宁到黄埔），第 1 步有 A 种不同的方法，第二步有 B 种不同的方法，……，第 n 步有 N 种不同的方法．那么完成这件事情一共有 A×B×……×N 种不同的方法．结合上个例子，老师要完成从家到黄埔的这么一件事，需要 2 个步骤，第 1 步是从家到长宁，一共 5 种选择；第 2 步从长宁到黄埔，一共 2 种选择；那么老师从家到黄埔一共有 5×2 个可选择的路线了，即 10 条．三、乘法原理解题三部曲 1、完成一件事分 N 个必要步骤； 2、每步找种数（每步的情况都不能单独完成该件事）； 3、步步相乘四、乘法原理的考题类型 7-2-3.乘法原理之染色问题.题库教师版 page 1 of 8

1、路线种类问题——比如说老师举的这个例子就是个路线种类问题； 2、字的染色问题——比如说要 3 个字，然后有 5 种颜色可以给每个字然后，问 3 个字有多少种染色方法； 3、地图的染色问题——同学们可以回家看地图，比如中国每个省的染色情况，给你几种颜色，问你一张包括几个部分的地图有几种染色的方法； 4、排队问题——比如说 6 个同学，排成一个队伍，有多少种排法； 5、数码问题——就是对一些数字的排列，比如说给你几个数字，然后排个几为数的偶数，有多少种排法．例题精讲【例 1】地图上有 A，B，C，D 四个国家(如下图)，现有红、黄、蓝三种颜色给地图染色，使相邻国家的颜色不同，但不是每种颜色都必须要用，问有多少种染色方法？ A C B D 【难度】3 星【题型】解答【考点】乘法原理之染色问题【解析】A 有 3 种颜色可选；    种；当 B，C 取相同的颜色时，有 2 种颜色可选，此时 D 也有 2 种颜色可选．根据乘法原理，不同的涂法有 3 2 2 12 当 B，C 取不同的颜色时，B 有 2 种颜色可选，C 仅剩 1 种颜色可选，此时 D 也只有 1 种颜色可选(与 A 相同)．根据乘法原理，不同的涂法有 3 2 1 1 6 综上，根据加法原理，共有12 6 18   种不同的涂法．     种．【答案】18 【巩固】如果有红、黄、蓝、绿四种颜色给例题中的地图染色，使相邻国家的颜色不同，但不是每种颜色都必须要用，问有多少种染色方法？【考点】乘法原理之染色问题【解析】第一步，首先对 A 进行染色一共有 4 种方法，然后对 B、C 进行染色，如果 B、C 取相同的颜色，有   种方法，D 剩下 2 种方法，对该图三种方式，D 剩下 3 种方式，如果 B、C 取不同颜色，有 3 2 6 的染色方法一共有 4 3 3 3 2 2      （）种方法．【题型】解答 84  【注意】给地图染色问题中有的可以直接用乘法原理解决，有的需要分类解决，前者分类做也可以解决问题．【答案】 84 【难度】3 星【例 2】在右图的每个区域内涂上 A 、 B 、 C 、 D 四种颜色之一，使得每个圆里面恰有四种颜色，则一共有__________种不同的染色方法． 1 3 6 4 7 2 5 【难度】4 星【考点】乘法原理之染色问题【解析】因为每个圆内 4 个区域上染的颜色都不相同，所以一个圆内的 4 个区域一共有 4 3 2    种染色方法．如右图所示，当一个圆内的1、2 、3 、4 四个区域的颜色染定后，由于 6 号区域的颜色不能与 2 、 3 、 4 三个区域的颜色相同，所以只能与1号区域的颜色相同，同理 5 号区域只能与 4 号区域的颜色相同， 7 号区域只能与 2 号区域的颜色相同，所以当1 、 2 、 3 、 4 四个区域的颜色染定后，其他区域的颜色也就相应的只有一种染法，所以一共有 24 种不同的染法．【题型】解答 24 【答案】 24 【例 3】如图，地图上有 A，B，C，D 四个国家，现用五种颜色给地图染色，要使相邻国家的颜色不相同，有多少种不同染色方法? 7-2-3.乘法原理之染色问题.题库教师版 page 2 of 8

A B C D 【考点】乘法原理之染色问题【解析】为了按要求给地图上的这四个国家染色，我们可以分四步来完成染色的工作：【题型】解答【难度】3 星第一步：给 A 染色，有 5 种颜色可选．第二步：给 B 染色，由于 B 不能与 A 同色，所以 B 有 4 种颜色可选．第三步：给 C 染色，由于 C 不能与 A 、 B 同色，所以 C 有 3 种颜色可选．第四步：给 D 染色，由于 D 不能与 B 、 C 同色，但可以与 A 同色，所以 D 有 3 种颜色可选．根据分步计数的乘法原理，用 5 种颜色给地图染色共有 5 4 3 3 180     种不同的染色方法．【答案】180 【巩固】如图，一张地图上有五个国家 A ， B ， C ， D ， E ，现在要求用四种不同的颜色区分不同国家，要求相邻的国家不能使用同一种颜色，不同的国家可以使用同—种颜色，那么这幅地图有多少着色方法？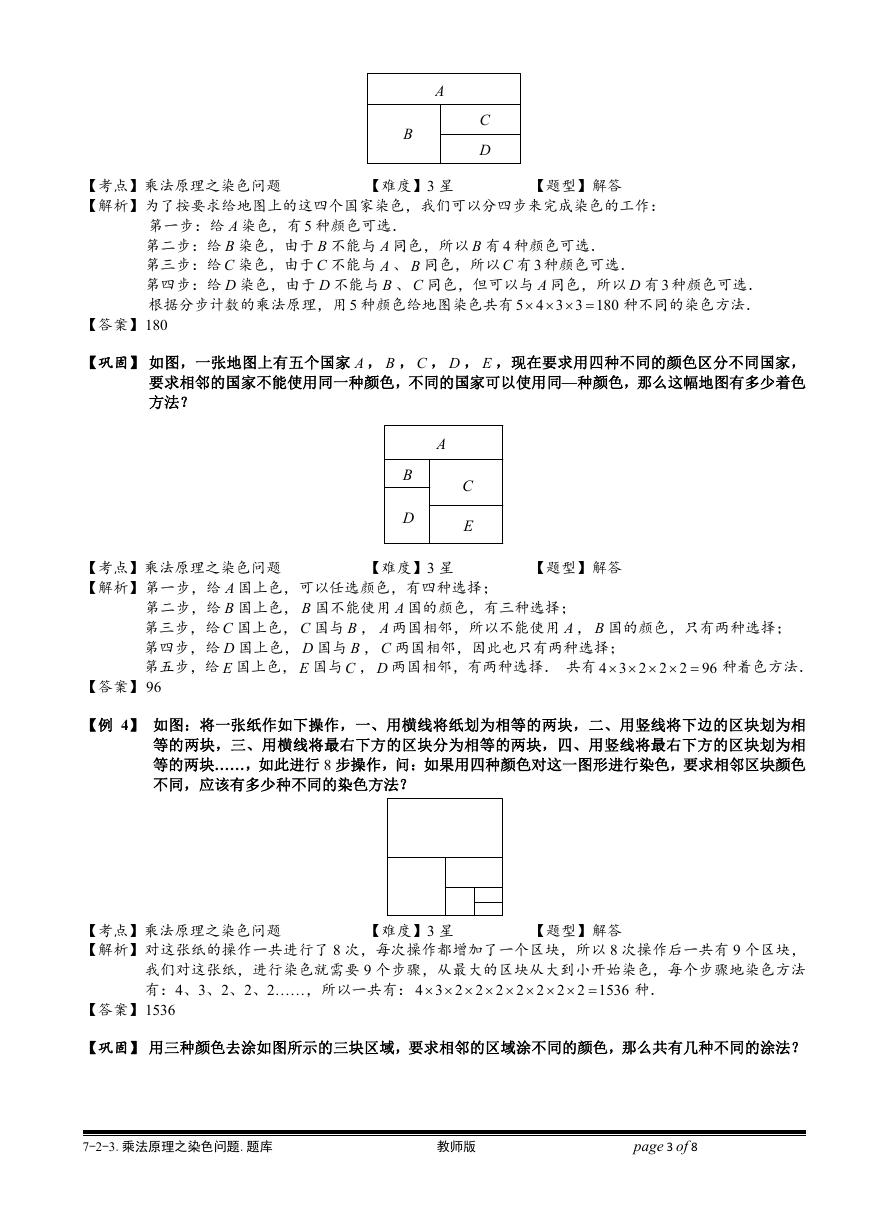 A C E B D 【考点】乘法原理之染色问题【解析】第一步，给 A 国上色，可以任选颜色，有四种选择；【难度】3 星【题型】解答第二步，给 B 国上色， B 国不能使用 A 国的颜色，有三种选择；第三步，给 C 国上色， C 国与 B ， A 两国相邻，所以不能使用 A ， B 国的颜色，只有两种选择；第四步，给 D 国上色， D 国与 B ， C 两国相邻，因此也只有两种选择；第五步，给 E 国上色， E 国与 C ， D 两国相邻，有两种选择．共有 4 3 2 2 2 96      种着色方法．【答案】 96 【例 4】如图：将一张纸作如下操作，一、用横线将纸划为相等的两块，二、用竖线将下边的区块划为相等的两块，三、用横线将最右下方的区块分为相等的两块，四、用竖线将最右下方的区块划为相等的两块……，如此进行 8 步操作，问：如果用四种颜色对这一图形进行染色，要求相邻区块颜色不同，应该有多少种不同的染色方法？【考点】乘法原理之染色问题【解析】对这张纸的操作一共进行了 8 次，每次操作都增加了一个区块，所以 8 次操作后一共有 9 个区块，我们对这张纸，进行染色就需要 9 个步骤，从最大的区块从大到小开始染色，每个步骤地染色方法有：4、3、2、2、2……，所以一共有： 4 3 2 2 2 2 2 2 2 1536          【题型】解答种．【难度】3 星【答案】1536 【巩固】用三种颜色去涂如图所示的三块区域，要求相邻的区域涂不同的颜色，那么共有几种不同的涂法？ 7-2-3.乘法原理之染色问题.题库教师版 page 3 of 8

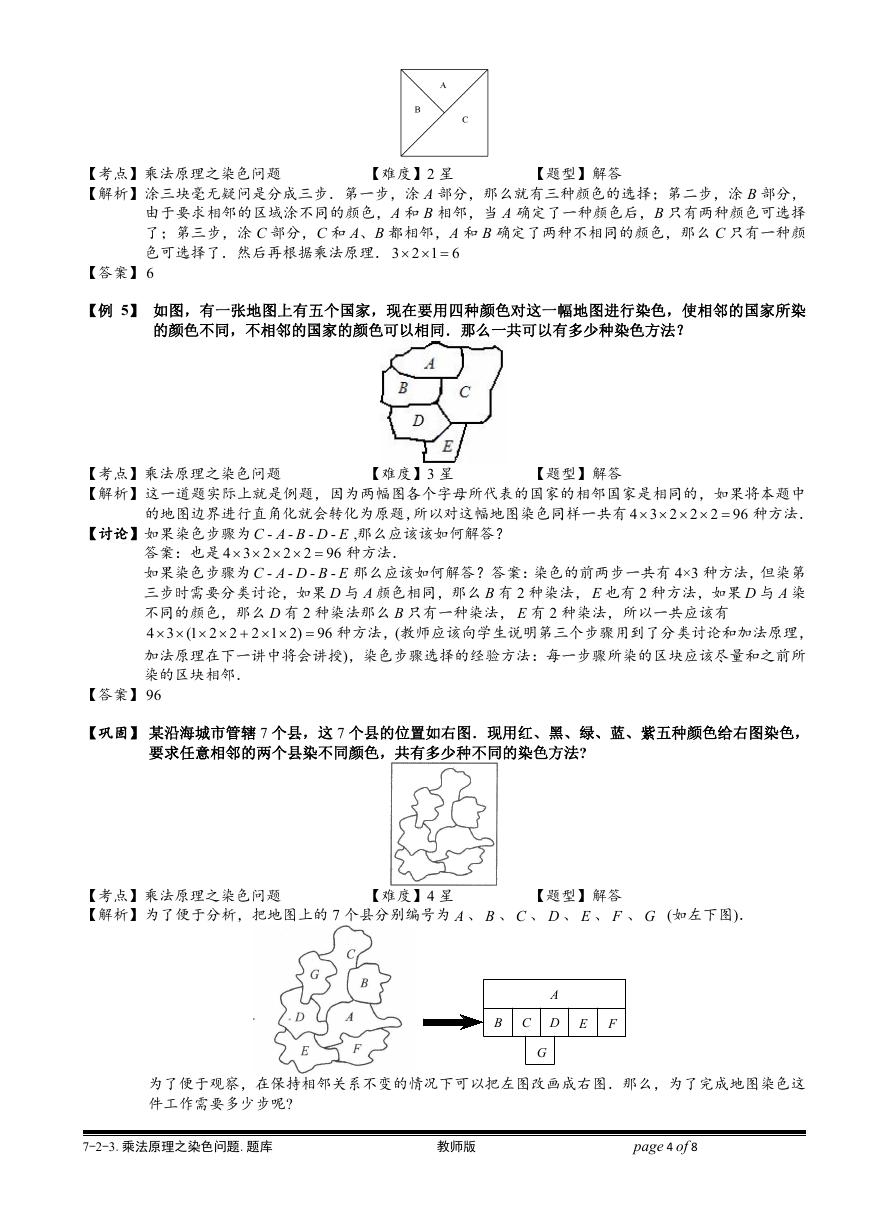
【考点】乘法原理之染色问题【解析】涂三块毫无疑问是分成三步．第一步，涂 A 部分，那么就有三种颜色的选择；第二步，涂 B 部分，由于要求相邻的区域涂不同的颜色，A 和 B 相邻，当 A 确定了一种颜色后，B 只有两种颜色可选择了；第三步，涂 C 部分，C 和 A、B 都相邻，A 和 B 确定了两种不相同的颜色，那么 C 只有一种颜色可选择了．然后再根据乘法原理． 3 2 1 6 【题型】解答    【难度】2 星【答案】 6 【例 5】如图，有一张地图上有五个国家，现在要用四种颜色对这一幅地图进行染色，使相邻的国家所染的颜色不同，不相邻的国家的颜色可以相同．那么一共可以有多少种染色方法？【考点】乘法原理之染色问题【解析】这一道题实际上就是例题，因为两幅图各个字母所代表的国家的相邻国家是相同的，如果将本题中      种方法．的地图边界进行直角化就会转化为原题，所以对这幅地图染色同样一共有 4 3 2 2 2 96 【题型】解答【难度】3 星【讨论】如果染色步骤为 - - - - -      种方法． C A B D E ,那么应该该如何解答？ - 答案：也是 4 3 2 2 2 96 C A D B E 那么应该如何解答？答案：染色的前两步一共有 4×3 种方法，但染第如果染色步骤为 - - 三步时需要分类讨论，如果 D 与 A 颜色相同，那么 B 有 2 种染法， E 也有 2 种方法，如果 D 与 A 染不同的颜色，那么 D 有 2 种染法那么 B 只有一种染法， E 有 2 种染法，所以一共应该有  种方法，(教师应该向学生说明第三个步骤用到了分类讨论和加法原理， 4 3 (1 2 2 2 1 2) 96        加法原理在下一讲中将会讲授)，染色步骤选择的经验方法：每一步骤所染的区块应该尽量和之前所染的区块相邻．【答案】 96 【巩固】某沿海城市管辖 7 个县，这 7 个县的位置如右图．现用红、黑、绿、蓝、紫五种颜色给右图染色，要求任意相邻的两个县染不同颜色，共有多少种不同的染色方法? 【考点】乘法原理之染色问题【解析】为了便于分析，把地图上的 7 个县分别编号为 A 、 B 、 C 、 D 、 E 、 F 、 G (如左下图)．【题型】解答【难度】4 星 B C A D G E F 为了便于观察，在保持相邻关系不变的情况下可以把左图改画成右图．那么，为了完成地图染色这件工作需要多少步呢? 7-2-3.乘法原理之染色问题.题库教师版 page 4 of 8

由于有 7 个区域，我们不妨按 A 、 B 、C 、 D 、 E 、 F 、G 的顺序，用红、黑、绿、蓝、紫五种颜色依次分 7 步来完成染色任务．第 1 步：先染区域 A ，有 5 种颜色可供选择；第 2 步：再染区域 B ，由于 B 不能与 A 同色，所以区域 B 的染色方式有 4 种；第 3 步：染区域 C ，由于 C 不能与 B 、 A 同色，所以区域 C 的染色方式有 3 种；第 4 步：染区域 D ，由于 D 不能与 C 、 A 同色，所以区域 D 的染色方式有 3 种；第 5 步：染区域 E ，由于 E 不能与 D 、 A 同色，所以区域 E 的染色方式有 3 种；第 6 步：染区域 F ，由于 F 不能与 E 、 A 同色，所以区域 F 的染色方式有 3 种；第 7 步：染区域 G ，由于 G 不能与 C 、 D 同色，所以区域 G 的染色方式有 3 种．根据分步计数的乘法原理，共有 5 4 3 3 3 3 3 4860        种不同的染色方法．【答案】 4860 【例 6】用 3 种颜色把一个 3 3 的方格表染色，要求相同行和相同列的 3 个格所染的颜色互不相同，一共有种不同的染色法．【考点】乘法原理之染色问题【解析】根据题意可知，染完后这个 3 3 的方格表每一行和每一列都恰有 3 个颜色．【题型】解答【难度】3 星用 3 种颜色染第一行，有 3 P  种染法；染完第一行后再染第一列剩下的 2 个方格，有 2 种染法； 3 当第一行和第一列都染好后，再根据每一行和每一列都恰有 3 个颜色对剩下的方格进行染色，可知其余的方格都只有唯一一种染法．所以，根据乘法原理，共有 3 2 6   种不同的染法． 6 【答案】 6 【例 7】如右图，有 A、B、C、D、E 五个区域，现用五种颜色给区域染色，染色要求：每相邻两个区域不同色，每个区域染一色．有多少种不同的染色方式？ B C A E D 【难度】3 星【题型】解答【考点】乘法原理之染色问题【解析】先采用分步：第一步给 A 染色，有 5 种方法；第二步给 B 染色，有 4 种方式；第三步给 C 染色，有 3 种方式；第四步给 D 染色，有 3 种方式；第五步，给 E 染色，由于 E 不能与 A、B、D 同色，但可以和 C 同色．此时就出现了问题：当 D 与 B 同色时，E 有 3 种颜色可染；而当 D 与 B 异色时，E 有 2 种颜色可染．所以必须从第四步就开始分类：第一类，D 与 B 同色．E 有 3 种颜色可染，共有 5 4 3 3 180     （种）染色方式；第二类，D 与 B 异色．D 有 2 种颜色可染，E 有 2 种颜色可染，共有 5 4 3 2 2 方式．根据加法原理，共有180 240      （种）染色（种）染色方式． 240 420   【注意】给图形染色问题中有的可以直接用乘法原理解决，但如果碰到有首尾相接的图形往往需要分类解决．【答案】 420 【巩固】如右图，有 A，B，C，D 四个区域，现用四种颜色给区域染色，要求相邻区域的颜色不同，每个区域染一色．有多少种染色方法？ A B D C 【难度】3 星【题型】解答【考点】乘法原理之染色问题【解析】A 有 4 种颜色可选，然后分类：第一类： B ， D 取相同的颜色．有 3 种颜色可染，此时 D 也有 3 种颜色可选．根据乘法原理，不同的染法有 4 3 3 36    （种）；第二类：当 B ， D 取不同的颜色时， B 有 3 种颜色可染，C 有 2 种颜色可染，此时 D 也有 2 种颜色可染．根据乘法原理，不同的染法有 4 3 2 2     （种）． 48 根据加法原理，共有 36 48 84   (种)染色方法． 7-2-3.乘法原理之染色问题.题库教师版 page 5 of 8

【答案】 84 【巩固】用四种颜色对右图的五个字染色，要求相邻的区域的字染不同的颜色，但不是每种颜色都必须要用．问：共有多少种不同的染色方法? 学而奥数【考点】乘法原理之染色问题【解析】第一步给“而”上色，有 4 种选择；思【难度】3 星【题型】解答然后对“学”染色，“学”有 3 种颜色可选；当“奥”，“数”取相同的颜色时，有 2 种颜色可选，此时“思”也有 2 种颜色可选，不同的涂法有 3 2 2 12    种；当“奥”，“数”取不同的颜色时，“奥”有 2 种颜色可选，“数”剩仅 1 种颜色可选，此时“思”也只有 1 种颜色可选(与“学”相同)，不同的涂法有 3 2 1 1 6 所以，根据加法原理，共有 4 3 (2 2 2)  种不同的涂法．     种．     72 【答案】 72 【例 8】分别用五种颜色中的某一种对下图的 A ， B ， C ， D ， E ， F 六个区域染色，要求相邻的区域染不同的颜色，但不是每种颜色都必须要用．问：有多少种不同的染法？ E C F D A B 【考点】乘法原理之染色问题【解析】先按 A ， B ， D ，C ， E 的次序染色，可供选择的颜色依次有 5，4，3，2，3 种，注意 E 与 D 的颜   (种)，其中有 3 种 E 和 D 同色，有 6 种 E 和 D 异色．最后染 F ，当 E 与 D 同色时  种染法．色搭配有 3 3 9 有 3 种颜色可选，当 E 与 D 异色时有 2 种颜色可选，所以共有 5 4 2 (3 3 6 2) 840       【题型】解答【难度】4 星【答案】 840 【例 9】将图中的○分别涂成红色、黄色或绿色，要求有线段相连的两个相邻○涂不同的颜色，共有多少种不同涂法？ A B D C 【考点】乘法原理之染色问题【解析】如右上图，当 A ，B ，C ，D 的颜色确定后，大正方形四个角上的○的颜色就确定了，所以只需求 A ，【题型】解答【难度】3 星 - - A B D C 的顺序涂颜色： B ， C ， D 有多少种不同涂法．按先 A ，再 B ， D ，后 C 的顺序涂色．按 - A 有 3 种颜色可选；当 B ， D 取相同的颜色时，有 2 种颜色可选，此时C 也有 2 种颜色可选，不同的涂法有3 2 2 12    种；当 B ， D 取不同的颜色时， B 有 2 种颜色可选， D 仅剩 1 种颜色可选，此时 C 也只有 1 种颜色可选 (与 A 相同)，不同的涂法有 3 2 1 1 6 所以，根据加法原理，共有12 6 18   种不同的涂法．     (种)．【答案】18 【例 10】用 4 种不同的颜色来涂正四面体（如图，每个面都是完全相同的正三角形）的 4 个面，使不同的面涂有不同的颜色，共有________种不同的涂法.（将正四面体任意旋转后仍然不同的涂色法，才 7-2-3.乘法原理之染色问题.题库教师版 page 6 of 8

被认为是不同的）【考点】乘法原理之染色问题【难度】4 星【题型】填空【关键词】迎春杯，中年级，复赛，第 9 题【解析】不旋转时共有 4×3×2×1=24 种染色方式，而一个正四面体有 4×3=12 种放置方法（4 个面中选 1 个作【解析】底面，再从剩余 3 个面中选 1 个作正面），所以每种染色方式被重复计算了 12 次，则不同的染色方法有 24÷12=2 种。【答案】 2 种【例 11】用红、橙、黄、绿、蓝 5 种颜色中的 1 种，或 2 种，或 3 种，或 4 种，分别涂在正四面体各个面上，一个面不能用两色，也无一个面不涂色的，问共有几种不同涂色方式？【题型】解答【考点】乘法原理之染色问题【解析】我们来看正四面体四个面的相关位置，当底面确定后，（从上面俯视）三个侧面的顺序有顺时针和逆【难度】4 星时针两种（当三个侧面的颜色只有一种或两种时，顺时针和逆时针的颜色分布是相同的）．按使用了的颜色种数分类：第一类：用了 4 种颜色．第一步，选 4 种颜色，相当于选 1 种不用，有 5 种选法．第二步，如果取   （种）涂法；第二类：用了 3 种颜色．第一步，选 3 种颜色，相当于选 2 种不用，有 5 4 2 10 定 4 种颜色涂于 4 个面上，有 2 种方法．这一类有 5 2 10    （种）选法；第二步，取定 3 种颜色如红、橙、黄 3 色，涂于 4 个面上，有 6 种方法，如下图①②③（图中用数字 1，2，3 分别表示红、橙、黄 3 色）．这一类有10 6 60   （种）涂法；第三类：用了 2 种颜色．第一步，选 2 种颜色，有 5 4 2 10 如红、橙 2 色，涂于 4 个面上，有 3 种方法，如下图④⑤⑥．这一类有10 3 30 法；    （种）选法；第二步，取定 2 种颜色   （种）涂第四类：用了一种颜色．第一步选 1 种颜色有 5 种方法；第二步，取定 1 种颜色涂于 4 个面上，只   （种）涂法．根据加法原理，共有10 60 30 5 105   （种）   有 1 种方法．这一类有 5 1 5 不同的涂色方式．【答案】105 【例 12】用红、黄、蓝三种颜色对一个正方体进行染色使相邻面颜色不同一共有多少种方法？如果有红、黄、蓝、绿四种颜色对正方体进行染色使相邻面颜色不同一共有多少种方法？如果有五种颜色去染又有多少种？(注：正方体不能翻转和旋转) 【难度】3 星【考点】乘法原理之染色问题【解析】如果一共只有三种颜色供染色，那么正方体的相对表面只能涂上一种颜色，一共有上下、左右、前【题型】解答后一共三组对立面，所以染色的方法有 3 2 1 6 如果有四种颜色，那么染色方法可分为两类，一类是从四种颜色中选取三种对正方体进行染色，一共有 4 3 2    种．另一种是四种颜色都染上，用这种染色方法，就允许有一组相对表面可以染上    种方法． 24 7-2-3.乘法原理之染色问题.题库教师版 page 7 of 8

不同的颜色，选取这组相对表面并染上不同颜色一共有 3 (4 3) 36 其他四个面只有 2 种方法，共 36 2 72   种，所以一共有 24 72 96 如果有 5 种颜色，那么用其中 3 种颜色的染色方法有 5 4 3 60 5 72 360  有 3 种方法，染色的方法有 5 4 3 2 1 120 正方体进行染色的方法就一共有 60 360 360 780    种．用其中 4 种颜色并拿去染色有  种，如果 5 种颜色都用，就有只有一组相对的表面染上相同的颜色，选取这组相对表面  种染色方法，用 5 种颜色对  种方法，用其余两种颜色去染  种方法．      种，一共有 3 120 360  种染色方法．       【答案】 780 【巩固】用 6 种不同的颜色来涂正方体的六个面，使得不同的面涂上不同的颜色一共有多少种涂色的方法？ (将正方体任意旋转之后仍然不同的涂色方法才被认为是相同的) 【考点】乘法原理之染色问题【解析】 (法 1)正方体 6 个面不同的涂色方法共有 6! 720 【难度】3 星【题型】解答与底面相邻的面有 4 种不同的选法．所以一个正方体的放置有 6 4 时候可以重复 24 次．所以可以染色的不同方法共有 720 24 30 (法 2)先涂正方体的一个面有 6 种方法，然后把这个面的对面涂上颜色不同的颜色，有 15 种涂法，再选择两种颜色，只有相邻和相对两种选法．如果相邻剩下两种颜色也相邻，如果相对剩下两种颜色也相对，所以共有15 2 30  种．固定一个底面共有 6 种不同的选法，选择一个 24   种不同的位置．即在旋转的 (种)．   种．   【答案】 30 【例 13】在“8×8”的方格中放棋子，每格至多放 l 枚棋子。若要求 8 行、8 列、30 条斜线(如下图所示)上的棋子数均为偶数。那么“8×8”的方格中最多可以放枚棋子。【考点】乘法原理之染色问题【难度】4 星【题型】填空【关键词】迎春杯，四年级，初赛，11 题【解析】对角线上不放，其他方格都放，那么一共放 64-8-8=48 个.证明：黑白染色后，如图，左图中所有直【解析】线共 8 条，都经过黑色格子且不重复，每条直线上的格子都是奇数个，所以每条直线上至少有一个格子不放棋子，所以黑格中至少有 8 个格子不放，同理白格中也至少有 8 个格子不能放，所以至少有 16 个格子不能放，最多放 48 个. 【答案】 48 个 7-2-3.乘法原理之染色问题.题库教师版 page 8 of 8

分享到：

赞收藏

资料库

7-2-3 乘法原理之染色法.教师版.doc

相关推荐

小学奥数

热门标签

最新资料