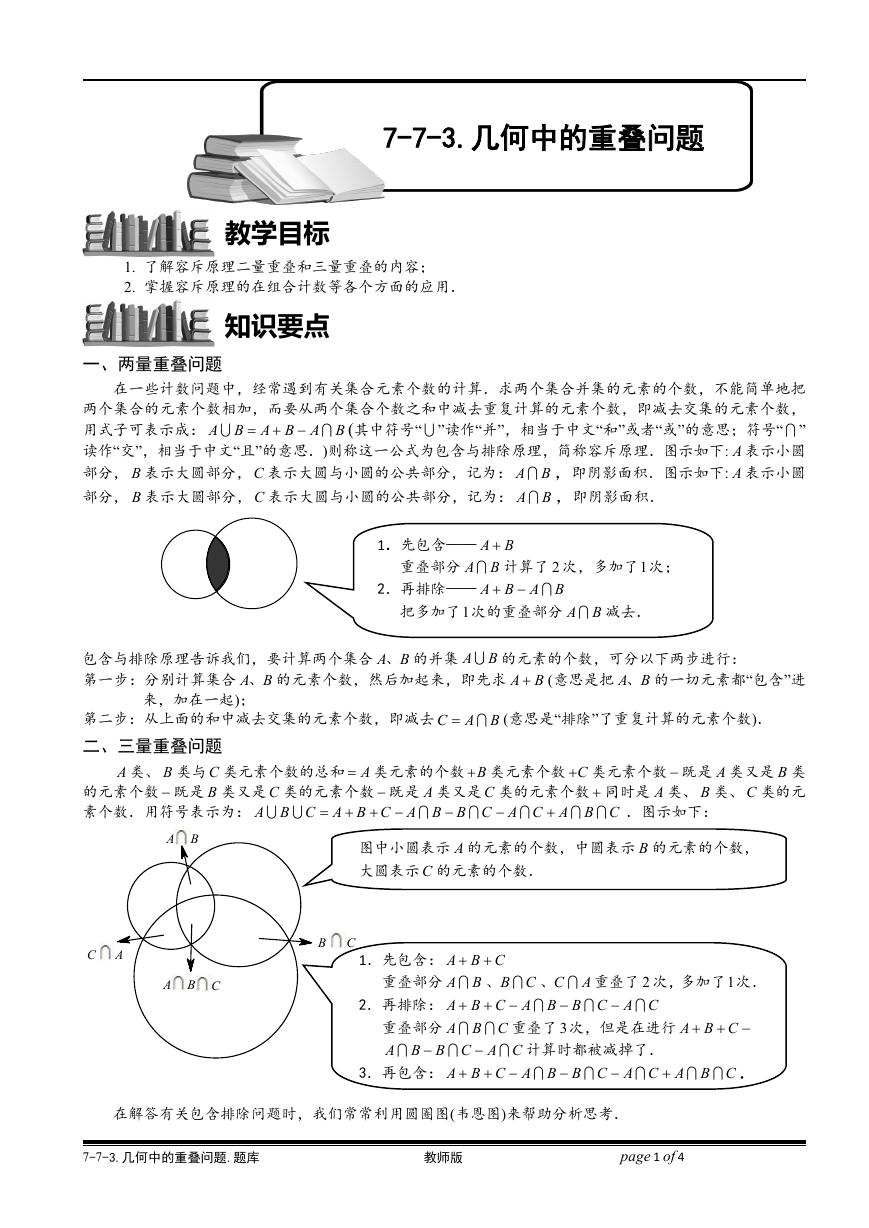
7-7-3.几何中的重叠问题 教学目标 1. 了解容斥原理二量重叠和三量重叠的内容； 2. 掌握容斥原理的在组合计数等各个方面的应用． 知识要点 一、两量重叠问题 在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把 两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，  (其中符号“  ”读作“并”，相当于中文“和”或者“或”的意思；符号“  ” 用式子可表示成： A B A B A B 读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下: A 表示小圆 部分， B 表示大圆部分， C 表示大圆与小圆的公共部分，记为： A B ，即阴影面积．图示如下: A 表示小圆 部分， B 表示大圆部分， C 表示大圆与小圆的公共部分，记为： A B ，即阴影面积．     1．先包含—— A B 重叠部分 A B 计算了 2 次，多加了1次； 2．再排除—— A B A B    把多加了1次的重叠部分 A B 减去． 包含与排除原理告诉我们，要计算两个集合 A B、 的并集 A B 的元素的个数，可分以下两步进行： 第一步：分别计算集合 A B、 的元素个数，然后加起来，即先求 A B (意思是把 A B、 的一切元素都“包含”进 来，加在一起)； 第二步：从上面的和中减去交集的元素个数，即减去 C A B 二、三量重叠问题   (意思是“排除”了重复计算的元素个数)． A 类、 B 类与 C 类元素个数的总和 A 类元素的个数 B 类元素个数 C 类元素个数  既是 A 类又是 B 类 的元素个数  既是 B 类又是 C 类的元素个数  既是 A 类又是 C 类的元素个数  同时是 A 类、 B 类、 C 类的元 素个数．用符号表示为： A B C A B C A B B C A C A B C   ．图示如下：             A B 图中小圆表示 A 的元素的个数，中圆表示 B 的元素的个数， 大圆表示 C 的元素的个数． C A B C 1．先包含： A B C   A B C 重叠部分 A B 、B C 、C A 重叠了 2 次，多加了1次．    2．再排除： A B C A B B C A C     重叠了 3 次，但是在进行 A B C 重叠部分 A B C A B B C A C  计算时都被减掉了．   3．再包含： A B C A B B C A C A B C                   ．  在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考． 7-7-3.几何中的重叠问题.题库 教师版 page 1 of 4 

例题精讲 【例 1】 把长 38 厘米和 53 厘米的两根铁条焊接成一根铁条．已知焊接部分长 4 厘米，焊接后这根铁条有多 长？ 【考点】几何中的重叠问题 【难度】1 星 【题型】解答 【解析】因为焊接部分为两根铁条的重合部分，所以，由包含排除法知，焊接后这根铁条长 38 53 4 87    (厘 米)． 【答案】87 厘米 【巩固】 把长 23 厘米和 37 厘米的两根铁条焊接成一根铁条．已知焊接部分长 3 厘米，焊接后这根铁条有多 长？ 【考点】几何中的重叠问题 【难度】1 星 【题型】解答 【解析】焊接部分为两根铁条的重合部分，由包含排除法知，焊接后这根铁条长： 23 37 3 57 【答案】57 厘米    (厘米)． 【例 2】 两张长 4 厘米，宽 2 厘米的长方形纸摆放成如图所示形状．把它放在桌面上，覆盖面积有多少平方 厘米？ 【考点】几何中的重叠问题 【难度】1 星 【题型】解答 4 厘 米 2 厘米 【解析】两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为 2 厘米的正方形，如 果利用两个 4 2 的长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各 被计算了一次，而实际上这部分只需计算一次就可以了．所以，被覆盖面积  长方形面积之和-重叠 部分．于是，被覆盖面积 4 2 2 2 2 12       (平方厘米)． 3 图 【答案】12 厘米 【巩固】 如图 3 ，一张长 8 厘米，宽 6 厘米，另一个正方形边长为 6 厘米，它们中间重叠的部分是一个边长为 4 厘米的正方形，求这个组合图形的面积． 【考点】几何中的重叠问题 【难度】1 星 【题型】解答 8 4 6 6 【解析】两个图形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为 4 厘米的正方形，如果 利用长方形和正方形面积之和来计算被覆盖桌面的面积，那么重叠部分在长方形和正方形面积中各 被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积  长方形面积  正 方形面积  重叠部分．于是，组合图形的面积： 8 6 6 6 4 4 68       (平方厘米)． 3 图 【答案】68 平方厘米 【巩固】 一个长方形长12 厘米，宽 8 厘米，另一个长方形长10 厘米，宽 6 厘米，它们中间重叠的部分是一个 边长 4 厘米的正方形，求这个组合图形的面积． 【考点】几何中的重叠问题 【难度】1 星 【题型】解答 7-7-3.几何中的重叠问题.题库 教师版 page 2 of 4 

12 4 8 6 10 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为 4 厘米的正方 【解析】 【解析】 形，如果利用两个长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了 一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积  长方形面积之和  重叠部分．于是， 组合图形的面积 12 8 10 6 4 4 140 【答案】140 平方厘米 (平方厘米)．        【例 3】 三个面积均为 50 平方厘米的圆纸片放在桌面上(如图)，三个纸片共同重叠的面积是10 平方厘米．三 个纸片盖住桌面的总面积是100 厘米．问：图中阴影部分面积之和是多少？ 【考点】几何中的重叠问题 【难度】2 星 【题型】解答 B A 10 C 【解析】将图中的三个圆标上 A 、 B 、 C ．根据包含排除法，三个纸片盖住桌面的总面积  ( A 圆面积 B 圆 面积 C 圆面积 ）（ A 与 B 重合部分面积 A 与 C 重合部分面积 B 与 C 重合部分面积 ） 三个纸片 共同重叠的面积，得：100 ）（ 与 B 重合部分面积 A 与 C 重合部分面积 B 与 C 重合  部分面积 10） ，得到 A 、 B 、 C 三个圆两两重合面积之和为：160 100 60  平方厘米，而这个面 积对应于圆上的那三个纸片共同重叠的面积的三倍与阴影部分面积的和，即：60 10 3   阴影部分 面积，则阴影部分面积为： 60 30 30 (平方厘米)． 50 50 50  （ A       【答案】30 平方厘米 【巩固】如图，已知甲、乙、丙 3 个圆的面积均为 30，甲与乙、乙与丙、甲与丙重合部分的面积分别为 6，8， 5，而 3 个圆覆盖的总面积为 73．求阴影部分的面积． 【考点】几何中的重叠问题 【难度】2 星 【题型】解答 【解析】设甲圆组成集合 A，乙圆组成集合 B，丙圆组成集合 C．    B   = A =30， A B =6， B C =8， A C =5， A B C   =73， A B C   . C A 而 A B C  有 73=30×3-6-8-5+ A B C   =2，即甲、乙、丙三者的公共面积(⑧部分面积)为 2．那 么只是甲与乙(④)，乙与丙(⑥)，甲与丙(⑤)的公共的面积依次为 6-2=4，8-2=6，5-2=3，所以有阴影 部分(①、②、③部分之和)的面积为 73-4-6-3-2=58． B C B C    ，即 A B C  A B A C      【答案】58 【例 4】 如图，三角形纸板、正方形纸板、圆形纸板的面积相等，都等于 60 平方厘米．阴影部分的面积总 和是 40 平方厘米，3 张板盖住的总面积是 100 平方厘米，3 张纸板重叠部分的面积是多少平方厘米？ 【考点】几何中的重叠问题 【难度】3 星 【题型】解答 【解析】阴影部分是有两块重叠的部分，被计算两次，而三张纸重叠部分是被计算了三次．所以三张纸重叠 部分的面积 60 3 100 40    （  ）   2 20 (平方厘米)． 7-7-3.几何中的重叠问题.题库 教师版 page 3 of 4 

【答案】20 平方厘米 【巩固】如图所示， A 、 B 、 C 分别是面积为12 、 28 、16 的三张不同形状的纸片，它们重叠在一起，露在 外面的总面积为 38 ．若 A 与 B 、 B 与 C 的公共部分的面积分别为 8 、 7 ， A 、 B 、 C 这三张纸片的 公共部分为 3 ．求 A 与 C 公共部分的面积是多少？ 【考点】几何中的重叠问题 【难度】3 星 【题型】解答 B A C 【解析】设 A 与 C 公共部分的面积为 x ，由包含与排除原理可得： ⑴ 先“包含”：把图形 A 、 B 、C 的面积相加：12 28 16 56    ，那么每两个图形的公共部分的面积 都重复计算了1次，因此要排除掉． ⑵ 再“排除”： 56 8 7 x ⑶ 再“包含”： 56 8 7 3x 根据上面的分析得： 56 8 7    ，这样一来，三个图形的公共部分被全部减掉，因此还要再补回．     ，这就是三张纸片覆盖的面积．      ，解得： 6 3 38 x  ． x 【答案】6 7-7-3.几何中的重叠问题.题库 教师版 page 4 of 4