7-8-1 几何计数（一）.学生版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：0.62M 资料格式：doc 举报版权申诉

第1页 / 共9页

第2页 / 共9页

第3页 / 共9页

第4页 / 共9页

第5页 / 共9页

第6页 / 共9页

第7页 / 共9页

第8页 / 共9页

【解析】如图：6条．

7-8-1 几何计数（一）教学目标 1.掌握计数常用方法； 2.熟记一些计数公式及其推导方法； 3.根据不同题目灵活运用计数方法进行计数．本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等，并渗透分类计数和用容斥原理的计数思想．知识要点一、几何计数在几何图形中，有许多有趣的计数问题，如计算线段的条数，满足某种条件的三角形的个数，若干个图分平面所成的区域数等等．这类问题看起来似乎没有什么规律可循，但是通过认真分析，还是可以找到一些处理方法的．常用的方法有枚举法、加法原理和乘法原理法以及递推法等．n 条直线最多将平面分成个部分；n 个圆最多分平面的部分数为 n(n-1)+2；n 个三角形将平面最多分成 2 2 3        n …… 2) n 2 ( n 1 2 3n(n-1)+2 部分；n 个四边形将平面最多分成 4n(n-1)+2 部分…… 在其它计数问题中，也经常用到枚举法、加法原理和乘法原理法以及递推法等．解题时需要仔细审题、综合所学知识点逐步求解．排列问题不仅与参加排列的事物有关，而且与各事物所在的先后顺序有关；组合问题与各事物所在的先后顺序无关，只与这两个组合中的元素有关．二、几何计数分类数线段：如果一条线段上有 n+1 个点(包括两个端点)（或含有 n 个“基本线段”），那么这 n+1 个点把这条线段一共分成的线段总数为 n+(n-1)+…+2+1 条数角：数角与数线段相似，线段图形中的点类似于角图形中的边．数三角形：可用数线段的方法数如右图所示的三角形（对应法），因为 DE 上有 15 条线段，每条线段的两端点与点 A 相连，可构成一个三角形，共有 15 个三角形，同样一边在 BC 上的三角形也有 15 个，所以图中共有 30 个三角形．数长方形、平行四边形和正方形：一般的，对于任意长方形（平行四边形），若其横边上共有 n 条线段，纵边上共有 m 条线段，则图中共有长方形（平行四边形）mn 个．例题精讲模块一、简单的几何计数【例 1】七个同样的圆如右图放置，它有_______条对称轴． 7-8-1.几何计数（一）.题库题库版 page 1 of 9

【考点】简单的几何计数【难度】1 星【题型】填空【关键词】迎春杯，六年级，初赛，试题【解析】如图：6 条．【答案】 6 条【例 2】下面的表情图片中：（A） 3 (B) 4 (C) 5 (D) 6 ，没有对称轴的个数为（）【考点】简单的几何计数【难度】2 星【题型】选择【关键词】华杯赛，初赛，第 1 题【解析】通过观察可知，第 1，2，5 这三张图片是有对称轴的，其他的 5 张图片都没有对称轴，所以没有对称轴的个数为 5，正确答案是 C。【答案】 C 【巩固】中心对称图形是：绕某一点旋转 180°后能和原来的图形重合的图形，轴对称图形是：沿着一条直线个。对折后两部分完全重合的图形，图的 4 个图形中，既是中心对称图形又是的轴对称图形的有【考点】简单的几何计数【难度】2 星【题型】填空【关键词】希望杯，五年级，一试，第 7 题【解析】共有 3 个，除第二个外其余都是。【答案】 3 个【例 3】两条直线相交所成的锐角或直角称为两条直线的“夹角”。现平面上有若干条直线，它们两两相交，并且“夹角”只能是 30°，60°或 90°。问：至多有多少条直线？【考点】简单的几何计数【难度】1 星【题型】填空【关键词】华杯赛，初赛，试题，第 12 题【解析】至多有 6 条直线，如图：【答案】 6 条【例 4】下图是王超同学为"环境保护专栏"设计的一个报头，用到基本的几何图形：线段、三角形、四边形、圆、弧线，其中用得最多的一种图形是________ 。【考点】简单的几何计数【难度】2 星【题型】填空【关键词】希望杯，四年级，二试，第 9 题【解析】观察图形发现是：线段最多【解析】【答案】线段最多 7-8-1.几何计数（一）.题库题库版 page 2 of 9

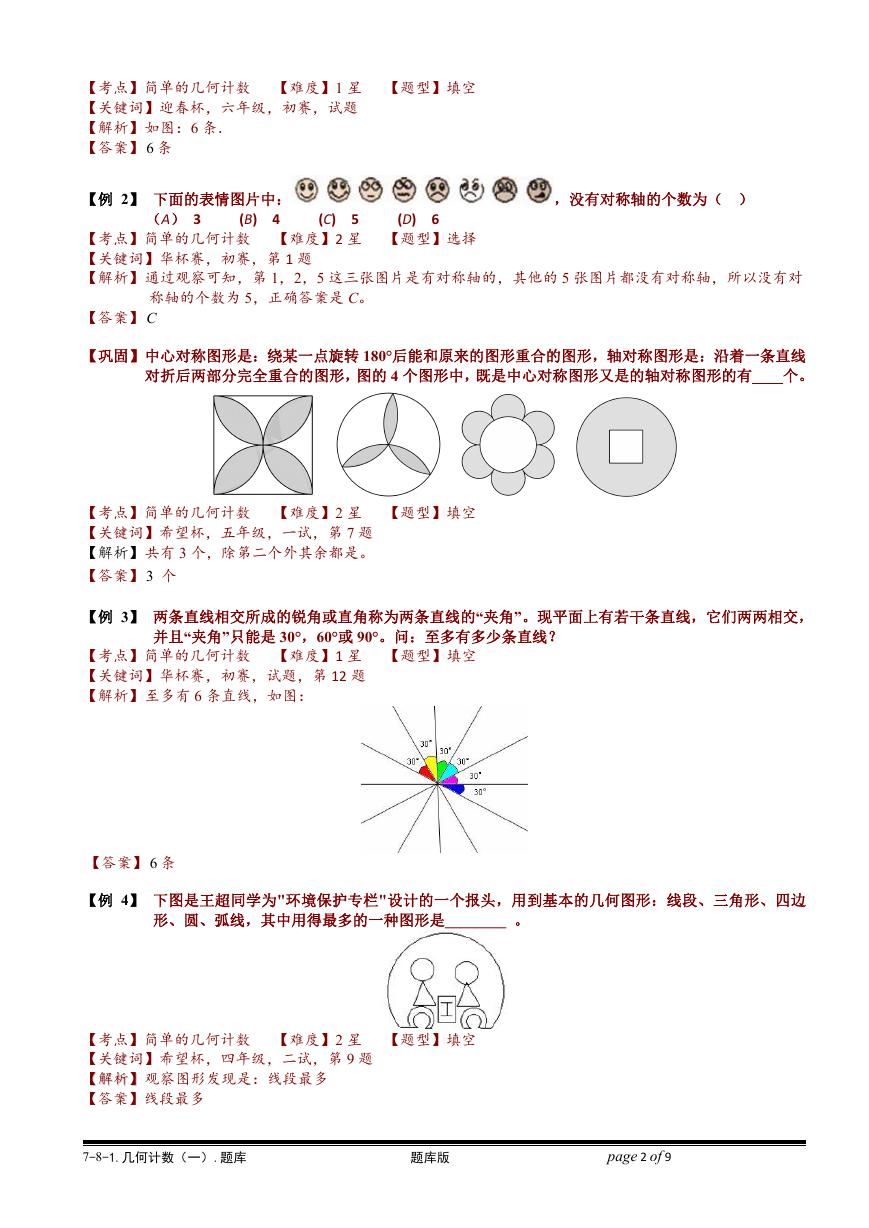
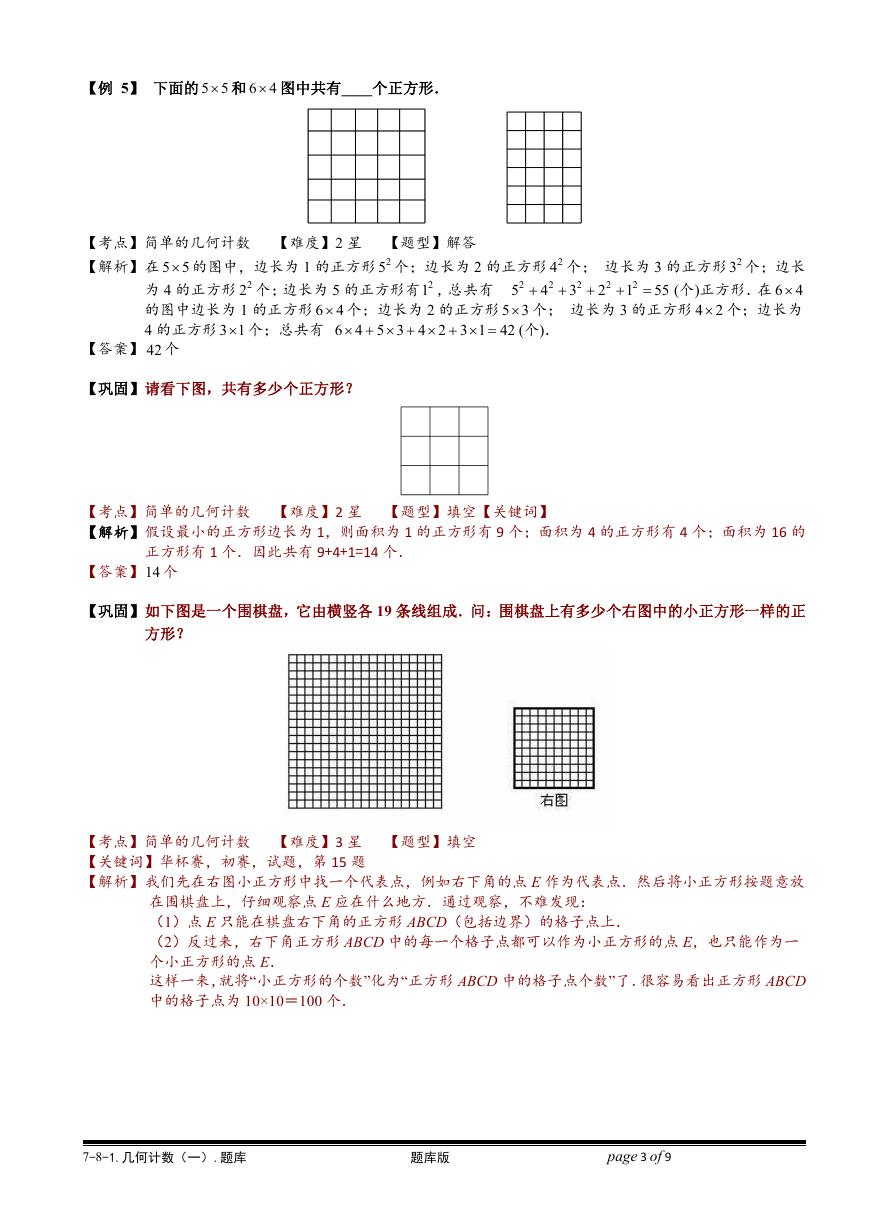
【例 5】下面的 5 5 和 6 4 图中共有____个正方形．【考点】简单的几何计数【难度】2 星【题型】解答【解析】在 5 5 的图中，边长为 1 的正方形 25 个；边长为 2 的正方形 24 个；边长为 3 的正方形 23 个；边长为 4 的正方形 22 个；边长为 5 的正方形有 21 ，总共有 2 (个)正方形．在 6 4 5 的图中边长为 1 的正方形 6 4 个；边长为 2 的正方形 5 3 个；边长为 3 的正方形 4 2 个；边长为 4 的正方形 3 1 个；总共有 6 4 5 3 4 2 3 1 42         (个)．  2 1 55 2 4  2 3   2 2  【答案】 42 个【巩固】请看下图，共有多少个正方形？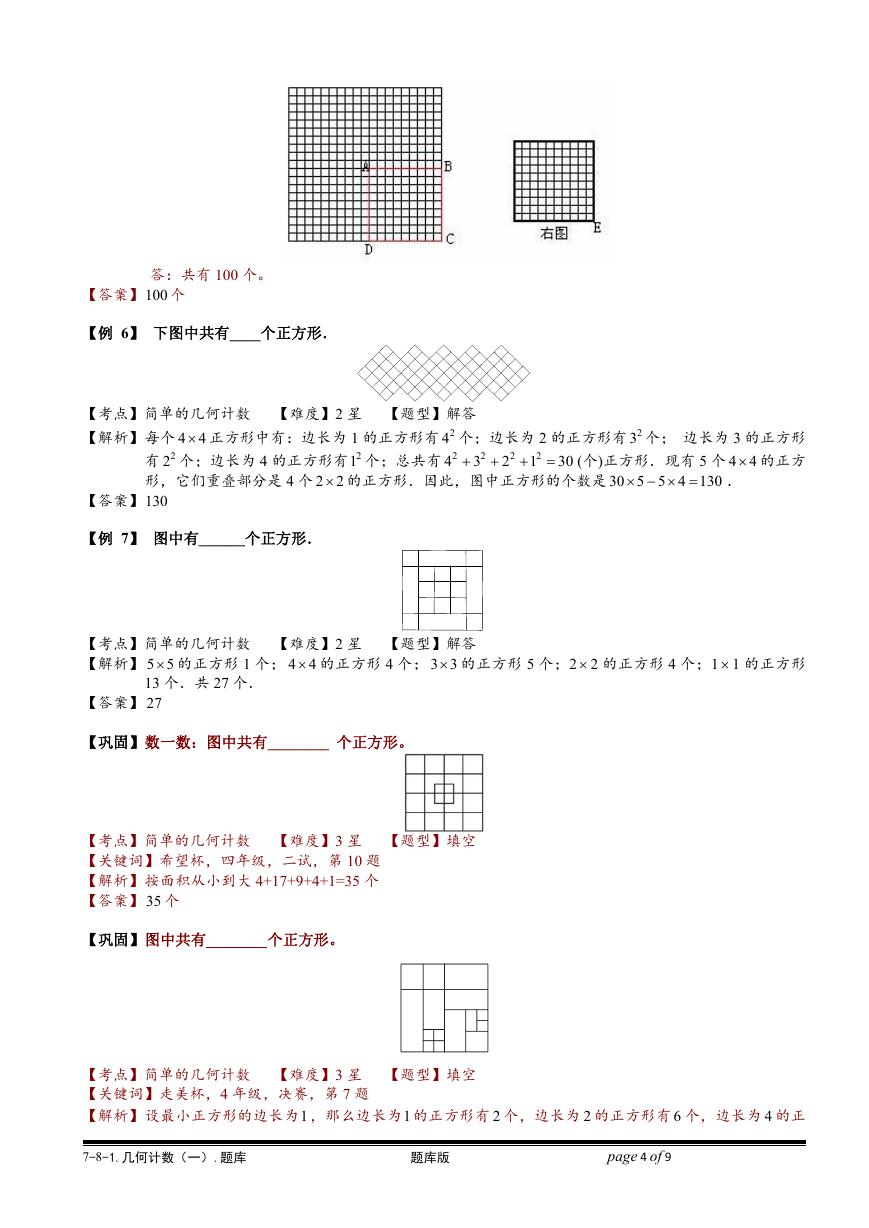【考点】简单的几何计数【难度】2 星【题型】填空【关键词】【解析】假设最小的正方形边长为 1，则面积为 1 的正方形有 9 个；面积为 4 的正方形有 4 个；面积为 16 的正方形有 1 个．因此共有 9+4+1=14 个．【答案】14 个【巩固】如下图是一个围棋盘，它由横竖各 19 条线组成．问：围棋盘上有多少个右图中的小正方形一样的正方形？【考点】简单的几何计数【难度】3 星【题型】填空【关键词】华杯赛，初赛，试题，第 15 题【解析】我们先在右图小正方形中找一个代表点，例如右下角的点 E 作为代表点．然后将小正方形按题意放在围棋盘上，仔细观察点 E 应在什么地方．通过观察，不难发现：（1）点 E 只能在棋盘右下角的正方形 ABCD（包括边界）的格子点上．（2）反过来，右下角正方形 ABCD 中的每一个格子点都可以作为小正方形的点 E，也只能作为一个小正方形的点 E．这样一来，就将“小正方形的个数”化为“正方形 ABCD 中的格子点个数”了．很容易看出正方形 ABCD 中的格子点为 10×10＝100 个． 7-8-1.几何计数（一）.题库题库版 page 3 of 9

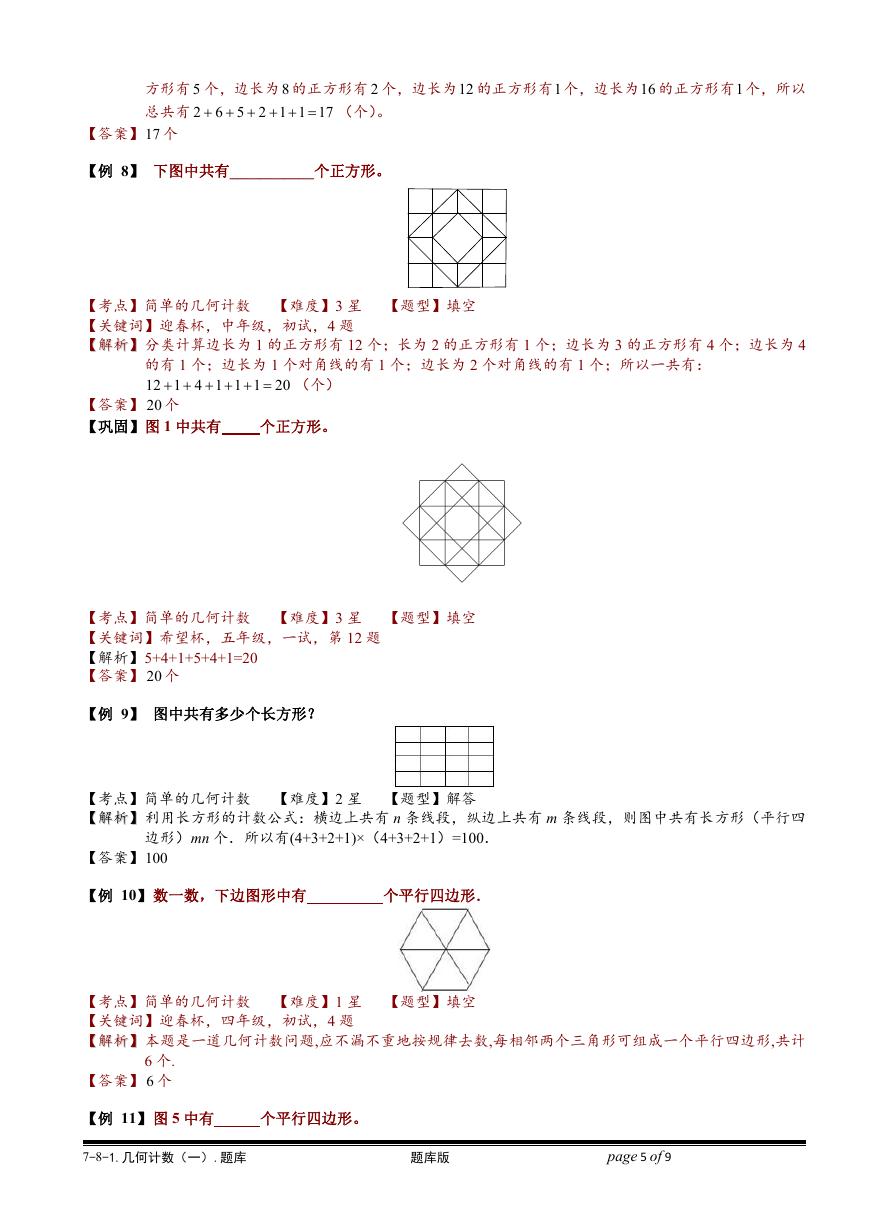
答：共有 100 个。【答案】100 个【例 6】下图中共有____个正方形．【考点】简单的几何计数【难度】2 星【题型】解答【解析】每个 4 4 正方形中有：边长为 1 的正方形有 24 个；边长为 2 的正方形有 23 个；边长为 3 的正方形 (个)正方形．现有 5 个 4 4 的正方有 22 个；边长为 4 的正方形有 21 个；总共有 2 4 形，它们重叠部分是 4 个 2 2 的正方形．因此，图中正方形的个数是 30 5 5 4 130     ．  2 1 2 2  30  2 3  【答案】130 【例 7】图中有______个正方形．【考点】简单的几何计数【难度】2 星【题型】解答【解析】 5 5 的正方形 1 个； 4 4 的正方形 4 个； 3 3 的正方形 5 个；2  2 的正方形 4 个；1  1 的正方形 13 个．共 27 个．【答案】 27 【巩固】数一数：图中共有________ 个正方形。【考点】简单的几何计数【难度】3 星【题型】填空【关键词】希望杯，四年级，二试，第 10 题【解析】按面积从小到大 4+17+9+4+1=35 个【答案】 35 个【巩固】图中共有个正方形。【考点】简单的几何计数【难度】3 星【题型】填空【关键词】走美杯，4 年级，决赛，第 7 题【解析】设最小正方形的边长为1 ，那么边长为1 的正方形有 2 个，边长为 2 的正方形有 6 个，边长为 4 的正 7-8-1.几何计数（一）.题库题库版 page 4 of 9

方形有 5 个，边长为 8 的正方形有 2 个，边长为12 的正方形有1个，边长为16 的正方形有1个，所以总共有 2 6 5 2 1 1 17       （个）。【答案】17 个【例 8】下图中共有___________个正方形。【考点】简单的几何计数【难度】3 星【题型】填空【关键词】迎春杯，中年级，初试，4 题【解析】分类计算边长为 1 的正方形有 12 个；长为 2 的正方形有 1 个；边长为 3 的正方形有 4 个；边长为 4 【解析】的有 1 个；边长为 1 个对角线的有 1 个；边长为 2 个对角线的有 1 个；所以一共有： 12 1 4 1 1 1 20       （个）【答案】 20 个【巩固】图 1 中共有个正方形。【考点】简单的几何计数【难度】3 星【题型】填空【关键词】希望杯，五年级，一试，第 12 题【解析】5+4+1+5+4+1=20 【答案】 20 个【例 9】图中共有多少个长方形？【考点】简单的几何计数【难度】2 星【题型】解答【解析】利用长方形的计数公式：横边上共有 n 条线段，纵边上共有 m 条线段，则图中共有长方形（平行四【解析】边形）mn 个．所以有(4+3+2+1)×（4+3+2+1）=100．【答案】100 【例 10】数一数，下边图形中有个平行四边形．【考点】简单的几何计数【难度】1 星【题型】填空【关键词】迎春杯，四年级，初试，4 题【解析】本题是一道几何计数问题,应不漏不重地按规律去数,每相邻两个三角形可组成一个平行四边形,共计【解析】 6 个. 【答案】 6 个【例 11】图 5 中有个平行四边形。 7-8-1.几何计数（一）.题库题库版 page 5 of 9

【考点】简单的几何计数【难度】2 星【题型】填空【关键词】希望杯，4 年级，1 试【解析】12+8+3=23 【答案】 23 【例 12】如右图中共有 7 层小三角形，求白色小三角形的个数与黑色小三角形的个数之比。【考点】简单的几何计数【难度】2 星【题型】填空【关键词】华杯赛，初赛，试题，第 10 题【解析】白色小三角形个数＝1＋2＋…＋6＝ 1 6   （） 2 6 ＝21，黑色小三角形个数＝1 十 2＋…＋7＝ 1 7   （） 2 7 ＝28，所以它们的比＝ 21 28 3 4 【答案】＝ 3 4 ，白色与黑色小三角形个数之比是 3 4 . 【例 13】如图，由小正方形构成的长方形网格中共有线段______条。【考点】简单的几何计数【难度】2 【题型】填空【关键词】希望杯，六年级，一试，第 8 题【解析】横的有 5×(1+2+3+4+5)=75 条，竖的有 6×(1+2+3+4)=60 条，一共 135 条【答案】135 条【例 14】图中线段的条数比三角形的个数多。【考点】简单的几何计数【难度】2 星【题型】填空【关键词】学而思杯，2 年级，第 6 题【解析】通过比较发现，线段的条数比三角形的个数多的正好是 6 条斜边。【答案】 6 【例 15】右图中共有个三角形。【考点】简单的几何计数【关键词】华杯赛，五年级，决赛，第 6 题【难度】2 星【题型】填空 7-8-1.几何计数（一）.题库题库版 page 6 of 9

【解析】由 1 个，2 个，3 个，4 个，6 个，8 个小三角形组成的三角形分别有：8，7，4，3，1，1 个，也即一共有 8+7+4+3+2=24 个。【答案】24 【例 16】如图 AB，CD，EF，MN 互相平行，则图中梯形个数与三角形个数的差是多少? 【考点】简单的几何计数【解析】图中共有三角形（1+2+3+4）×4=40 个．梯形（1+2+3+4）×（2+4）=60；所以梯形比三角形多 60-40=20 【难度】3 星【题型】解答个．【答案】 20 个【例 17】右边三个图中，都有一些三角形，在图 A 中，有 ____个；在图 B 中，有______个；中图 C 中，有______ 个。【考点】简单的几何计数【难度】2 星【题型】填空【关键词】希望杯，4 年级，1 试【解析】图 A 5 个; 8 个; 图 B 图 C 5 个【例 18】请看下图，共有多少个三角形？【考点】简单的几何计数【解析】独立的三角形有 7 个，由 4 个三角形组成的三角形有 1 个，加上最大的三角形，因此共有 7+1+1=9 【难度】2 星【题型】填空个三角形．【答案】 9 【例 19】右图中共有个三角形．【考点】简单的几何计数【难度】2 星【题型】填空【关键词】迎春杯，三年级，初赛，2 题【解析】分类枚举得到：边长是1个单位长度的有12 个三角形；【解析】边长是 2 个单位长度的有 6 个三角形边长是 3 个单位长度的有 2 个三角形 7-8-1.几何计数（一）.题库题库版 page 7 of 9

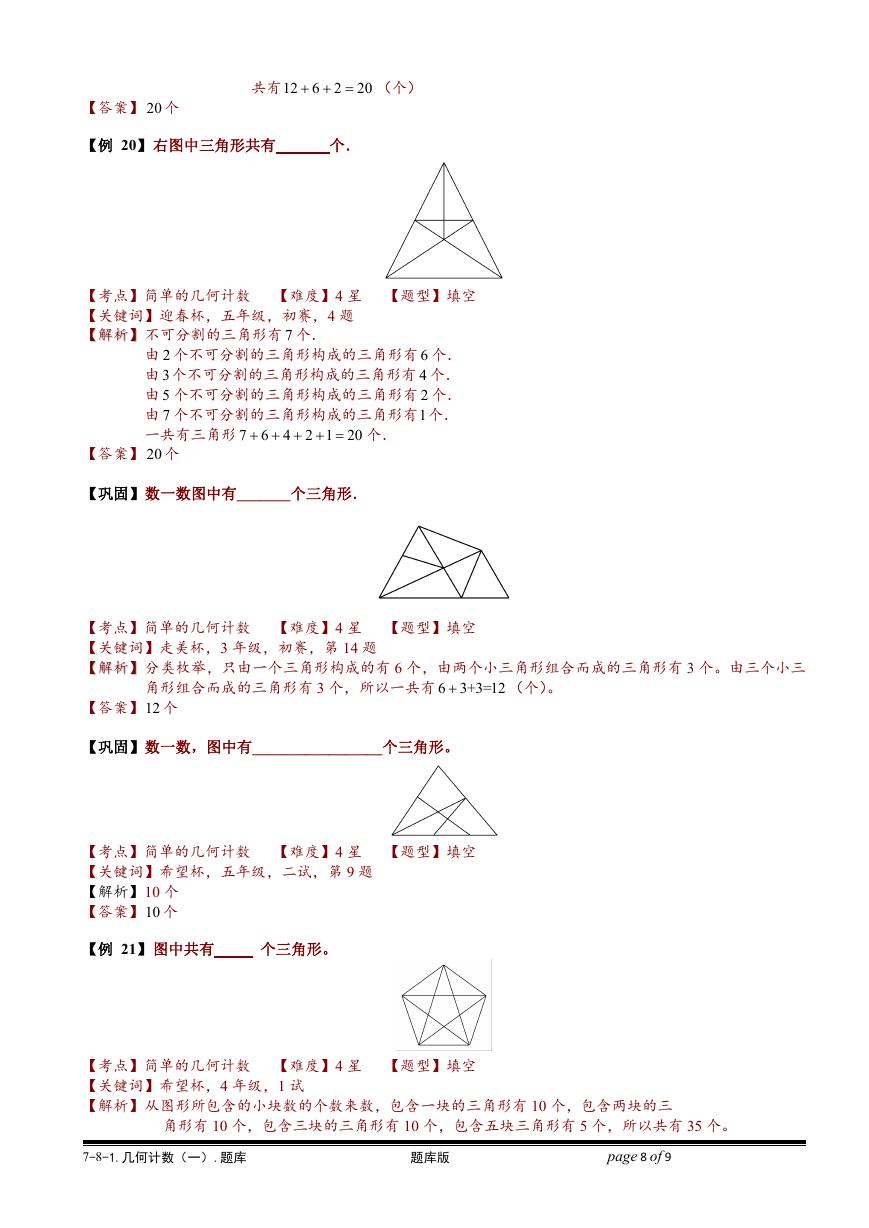
【答案】 20 个共有12 6 2    （个） 20 【例 20】右图中三角形共有个．【考点】简单的几何计数【难度】4 星【题型】填空【关键词】迎春杯，五年级，初赛，4 题【解析】不可分割的三角形有 7 个．【解析】由 2 个不可分割的三角形构成的三角形有 6 个．由 3 个不可分割的三角形构成的三角形有 4 个．由 5 个不可分割的三角形构成的三角形有 2 个．由 7 个不可分割的三角形构成的三角形有1个．一共有三角形 7 6 4 2 1 20      个．【答案】 20 个【巩固】数一数图中有_______个三角形．【考点】简单的几何计数【难度】4 星【题型】填空【关键词】走美杯，3 年级，初赛，第 14 题【解析】分类枚举，只由一个三角形构成的有 6 个，由两个小三角形组合而成的三角形有 3 个。由三个小三【解析】角形组合而成的三角形有 3 个，所以一共有 6 3+3=12  （个）。【答案】12 个【巩固】数一数，图中有_________________个三角形。【考点】简单的几何计数【难度】4 星【题型】填空【关键词】希望杯，五年级，二试，第 9 题【解析】10 个【答案】10 个【例 21】图中共有个三角形。【考点】简单的几何计数【难度】4 星【题型】填空【关键词】希望杯，4 年级，1 试【解析】从图形所包含的小块数的个数来数，包含一块的三角形有 10 个，包含两块的三角形有 10 个，包含三块的三角形有 10 个，包含五块三角形有 5 个，所以共有 35 个。 7-8-1.几何计数（一）.题库题库版 page 8 of 9

分享到：

赞收藏

资料库

7-8-1 几何计数（一）.学生版.doc

相关推荐

小学奥数

热门标签

最新资料