4-2-2 巧求周长.教师版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：1.95M 资料格式：doc 举报版权申诉

第1页 / 共23页

第2页 / 共23页

第3页 / 共23页

第4页 / 共23页

第5页 / 共23页

第6页 / 共23页

第7页 / 共23页

第8页 / 共23页

文本预览

4-2-2.巧求周长知识点拨一、基本概念 ①周长：封闭图形一周的长度就是这个图形的周长． ②面积：物体的表面或封闭图形的大小，叫做它们的面积．二、基本公式： ①长方形的周长 2  (长  宽)，面积  长  宽． ②正方形的周长 4  边长，正方形的面积  边长  边长．三、常用方法：（1）对于基本的长方形和正方形图形，可以直接用公式求出它们的周长和面积，对于一些不规则的比较复杂的几何图形，我们可以采用转化的数学思想方法割补成基本图形，利用长方形、正方形周长及面积计算的公式求解．（2）转化是一种重要的数学思想方法，在转化过程中要抓住“变”与“不变”两个部分．转化后的图形虽然形状变了，但其周长和面积不应该改变，所以在求解过程中不能遗漏掉某些线段的长度或某部分图形的面积．转化的目标是将复杂的图形转化为周长或面积可求的图形．（3）寻求正确有效的解题思路，意味着寻找一条摆脱困境、绕过障碍的途径．因此，我们在解决数学问题时，思考的着重点就是要把所需解决的问题转化为已经能够解决的问题．也就是说，在直接求解不容易或很难找到解题途径的问题时，我们往往转化问题的形式，从侧面或反面寻找突破口，知道最终把它转化成一个或若干个能解决的问题．这种解决问题的思想在数学中叫“化归”，它是数学思维中重要的思想和方法．（4）在几何中，有许多图形是由一些基本图形组合、拼凑而成的．这样的图形我们称为不规则图形．不规则图形的面积往往无法直接应用公式计算．那么，不规则图形的面积怎样去计算呢？对称、旋转、平移这几种几何变换就是解决这类面积问题的手段．四、几个重要的解题思想（1）平移在平面图形的计算中，常常要将一个平面图形移动到平面上的另一个位置进行计算．其中，将图形沿一个固定方向的移动叫做平移，一个图形经过平行移动不改变其形状与大小，所以图形面积是保持不变的．利用图形的平移，可以使面积计算问题的解法简捷明快，颇有新意．（2）割补割补法在我国古代叫“出入相补原理”，我国古代魏晋时期著名的数学家刘徽在《九章算术注》中就明确地提出“出入相补，各从其类”的出入相补原理．这个原理的内容是几何图形经过分、合、移、补所拼凑成的教师寄语：拼一个春夏秋冬，换一生无怨无悔。 1

新图形，它的面积不变．（3）旋转在平面图形的割补中，有时要将一个图形绕定点旋转到一个新的位置，产生一种新的图形结构，图形在转动过程中形状大小不发生改变．利用这种新的图形结构可以帮我们解决面积的计算问题．（4）对称平面图形中有许多简单漂亮的图形都是轴对称图形．轴对称图形沿对称轴折叠，轴两侧可以完全重合．也就是说，如果一个图形是轴对称图形，那么对称轴平分这个图形的面积．熟悉轴对称图形这个性质，对面积计算会有很大帮助．（5）代换在几何计算中，对有关数量进行适当的等量代换也是解决问题的已知技巧．小结：本讲主要通过求一些不规则图形的周长，体会一种转化思想，重点在于把不规则图形转化为规则图形的方法，包括平移、旋转、割补、差不变原理，通过这些方法的学习，让学生体会求周长的技巧，提高学生的观察能力、动手操作能力、综合运用能力．例题精讲模块一、图形的周长和面积——割补法【例 1】求图中所有线段的总长(单位：厘米)    ；   4 3 BE BC CD DE 【考点】巧求周长【难度】2 星【题型】填空【解析】要注意到，题目所求的是图中所有线段的总长，而图中的线段，并不仅仅是 AB 、BC 、CD 、DE 四段，还包括 AC 、 BE 等等，因此不能简单地将图中标示的线段长度进行求和．同时应该注意到， AC AB BC ，等等．因此，为了计算图中所有线段的总长，需要先计算 AB 、 BC 、 CD 、 DE 这四条线段分别被累加了几次．这里，可以按照每条线段分别是由几部分组成的加以讨论：由 1 段组成的线段共有 4 条，即 AB 、 BC 、 CD 、 DE ，而求和过程中 AB 、 BC 、 CD 、 DE 这四条线段各被累加了 1 次．类似地考虑到，由 2 段组成的线段共有 3 条，求和过程中 AB 、 DE 各被累加了 1 次, BC 、 CD 各被累加了 2 次．由 3 段组成的线段共有 2 条，求和过程中 AB 、DE 各被累加了 1 次，BC 、CD 各被累加了 2 次．由 4 段组成的线段只有 AE，其中 AB 、 BC 、 CD 、 DE 各被计算了 1 次．综上所述， AB 、 DE 各被计算了 4 次， BC 、 CD 各被计算了 6 次．因而图中所有线段的总长度为：    3 1 =48      3 1 2 6 （厘米） 4 2   4 6      【答案】 48 【例 2】如图所示，点 B 是线段 AD 的中点，由 A 、 B 、 C 、 D 四个点所构成的所有线段的长度均为整数，若这些线段的长度之积为 10500，则线段 AB 的长度是。【考点】巧求周长【难度】2 星【题型】填空【关键词】华杯赛，决赛，第 7 题，10 分【解析】线段所有长度包括 AB 、 BC 、CD 、 AC 、 BD 、 AD 。由于最后要求的是 AB ，我们可用 AB 和 BC 来表示这所有线段之积，为：   10500  对 10500 进行分解质因式，可得 AB BC AB BC        AB BC  2 10500=2 【答案】 5 3 2 AB  3 3 5   2   AB BC AB  7  所以 AB 长度为 5 。   AB BC    AB BC   教师寄语：拼一个春夏秋冬，换一生无怨无悔。 2

【例 3】三只猴子走得一样快，所走的路线如下图。哪只猴子先吃到桃子，就在它旁边的( )里画勾。【考点】巧求周长【难度】2 星【题型】填空【关键词】走美杯，3 年级，决赛，第 9 题，12 分【解析】猴子走的路线应该分为横向与竖向，两个纬度来看，横向看三只猴子所走路线是相同的，竖向看 A 走的路程最少，所以 A 先吃到桃子。【答案】 A 【例 4】在一个长方形的面积为 169 平方厘米。在这个长方形内任取一点 P，则点 P 到长方形四边的距离之和最小值为_______厘米。【考点】巧求周长【难度】2 星【题型】填空【关键词】走美杯，四年级，初赛，第 13 题【解析】容易知道，无论点 P 在长方形内的位置在哪，P 点到则点 P 到长方形四边的距离之和都为该长方形的“长+宽”，若“长+宽”最小，则长与宽的差要尽量小，即长=宽=13 厘米时，P 到长方形四边的距离之和最小，为 26 厘米。【答案】 26 厘米【例 5】边长是15 厘米的 3 个正方形拼成一个长方形，这个长方形的周长是多少？【考点】巧求周长【难度】2 星【题型】解答【解析】想一想，把几个正方形拼合在一起，拼出的长方形的周长与所有正方形的周长相差多少呢？由 3 个大小相同正方形拼成一个长方形，只有一种拼法，就是把三个正方形排成一排．于是拼成的长方形的长是15 3 45 所以长方形的周长是：(长  宽) 2   厘米，宽是15 厘米． 45 15  (厘米)．   ） 2 120   （【答案】120 厘米【巩固】用一块长8 分米，宽 4 分米的长方形纸板与两块边长 4 分米的正方形纸板拼成一个正方形．拼成的正方形的周长是多少分米？ 8 4 【难度】3 星【题型】解答【考点】巧求周长【解析】两块边长 4 分米的正方形纸可以拼成一个长 8 分米，宽 4 分米的长方形纸板，与原有的一块8 分米，宽 4 分米的长方形纸板的面积一样大，而且这两个长方形两条宽的和正好等于一条长．所以，拼法如图所示．然后运用正方形的周长计算公式很容易求出它的周长．教师寄语：拼一个春夏秋冬，换一生无怨无悔。 3

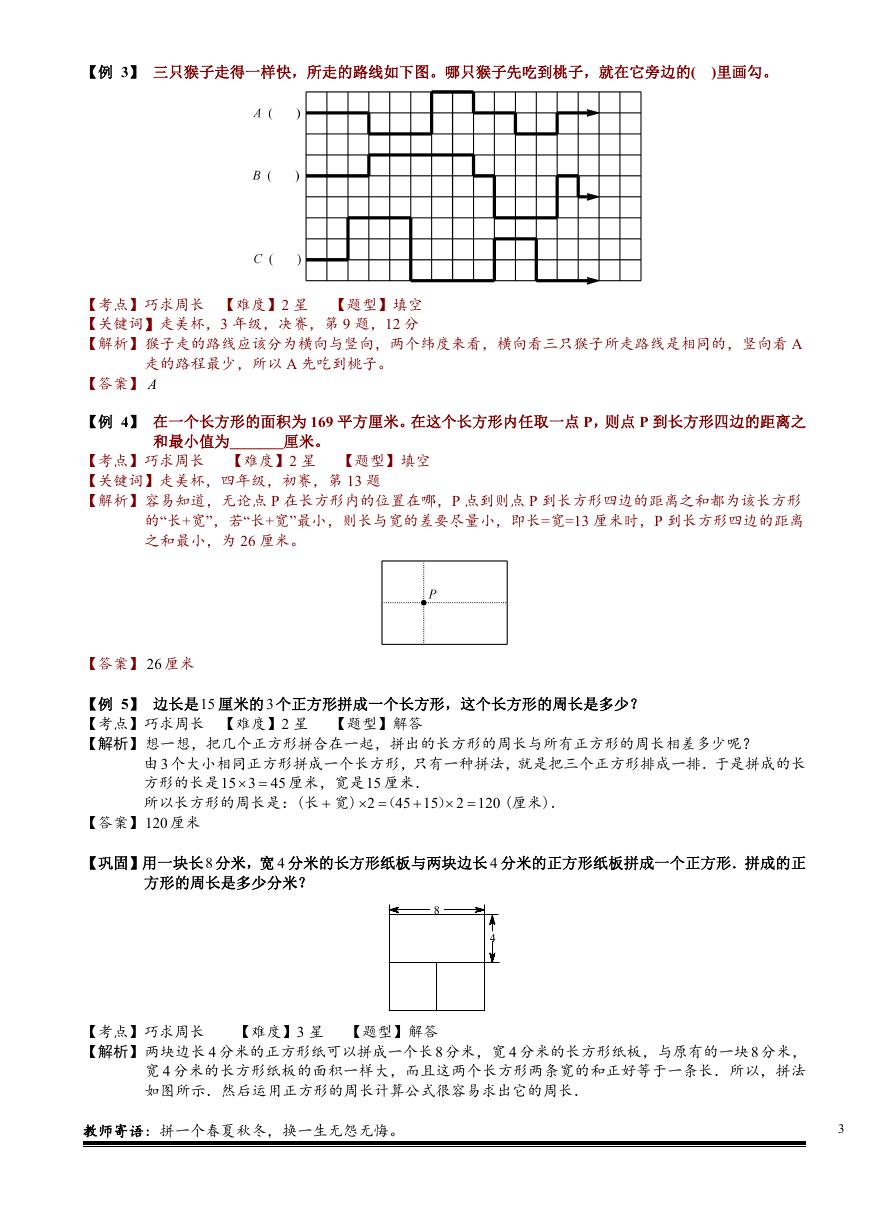
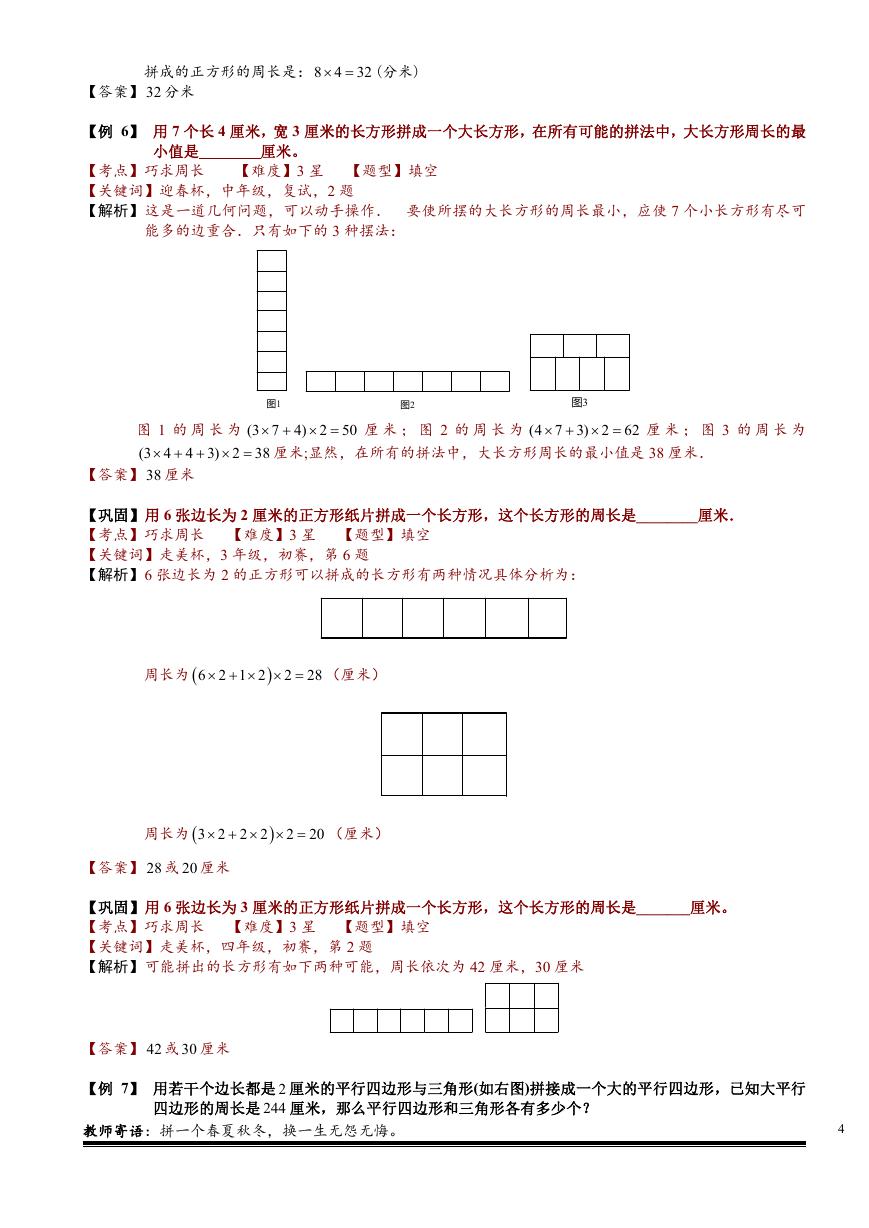
拼成的正方形的周长是：8 4 32   【答案】 32 分米 (分米) 【例 6】用 7 个长 4 厘米，宽 3 厘米的长方形拼成一个大长方形，在所有可能的拼法中，大长方形周长的最厘米。小值是【考点】巧求周长【关键词】迎春杯，中年级，复试，2 题【解析】这是一道几何问题，可以动手操作．要使所摆的大长方形的周长最小，应使 7 个小长方形有尽可【难度】3 星【题型】填空能多的边重合．只有如下的 3 种摆法：图1 图2 图3 图 1 的周长为 (3 7 4) 2 50 (3 4 4 3) 2 38      【答案】 38 厘米   厘米；图 2 的周长为 (4 7 3) 2 62   厘米；图 3 的周长为     厘米;显然，在所有的拼法中，大长方形周长的最小值是 38 厘米．【巩固】用 6 张边长为 2 厘米的正方形纸片拼成一个长方形，这个长方形的周长是________厘米．【考点】巧求周长【难度】3 星【题型】填空【关键词】走美杯，3 年级，初赛，第 6 题【解析】6 张边长为 2 的正方形可以拼成的长方形有两种情况具体分析为：周长为 6 2 1 2       （厘米） 28 2 周长为 3 2 2 2     【答案】 28 或 20 厘米   （厘米） 20 2 【巩固】用 6 张边长为 3 厘米的正方形纸片拼成一个长方形，这个长方形的周长是_______厘米。【考点】巧求周长【难度】3 星【题型】填空【关键词】走美杯，四年级，初赛，第 2 题【解析】可能拼出的长方形有如下两种可能，周长依次为 42 厘米，30 厘米【答案】 42 或 30 厘米【例 7】用若干个边长都是 2 厘米的平行四边形与三角形(如右图)拼接成一个大的平行四边形，已知大平行四边形的周长是 244 厘米，那么平行四边形和三角形各有多少个？教师寄语：拼一个春夏秋冬，换一生无怨无悔。 4

【考点】巧求周长【难度】3 星【题型】解答【解析】大平行四边形上、下两边的长为 (244 2 2) 2 120   的边，所以共有小平行四边形120 6 2 40 个．【答案】平行四边形 40 个，三角形 40 个   厘米，观察上边，每 6 厘米有两个平行四边形    个，而三角形的数量与小平行四边形的数量相等，也是 40 【巩固】用若干个边长都是 2 厘米的平行四边形与三角形(如右图)拼接成一个大的平行四边形，已知大平行四边形的周长是 236 厘米，那么平行四边形和三角形各有多少个？【考点】巧求周长【难度】3 星【题型】解答【解析】大平行四边形上、下两边的长为 (236 2 2) 2 116     厘米，观察上边，每 6 厘米有两个平行四边形的边，116 6 19    ，所以有三角形19 2 38   个，小平行四边形 38 1 39   个． 2 【答案】三角形 38 个，平行四边形 39 个【例 8】将一个边长为 4 厘米的正方形对折，再沿折线剪开，得到两个长方形．请问：这两个长方形的周长之和比原来正方形的周长多几厘米？【考点】巧求周长【解析】剪开后的图形与原图形相比，多了两条边，这两条边的长度即为所求． 4 2=8 【答案】 8 【难度】1 星【题型】解答  （厘米）。【巩固】把一个边长为 a 的正方形分成两个完全相同的长方形，则这两个长方形的周长的和是【考点】巧求周长【难度】1 星【题型】填空【关键词】希望杯，4 年级，初赛，12 题【解析】剪开后的图形与原图形相比，多了两条边，这两条边的长度为 2a ，所以这两个长方形的长度为。 4 a 【答案】 6a  2 a  6 a 【巩固】如图，两个长方形拼成了一个正方形。如果正方形的周长比两个长方形的周长的和少 6 厘米，则正方形面积是________平方厘米。【考点】巧求周长【难度】1 星【题型】填空【关键词】希望杯，4 年级，初赛【解析】正方形的周长比两个长方形的周长的和少 2 个边长,2 个边长是 6 厘米,则边长是 3 厘米,面积是 9 平方厘米. 【答案】 9 平方厘米【巩固】两个大小相同的正方形拼成了一个长方形，长方形的周长比原来的两个正方形周长的和减少了 6 厘米，原来一个正方形的周长是多少厘米？教师寄语：拼一个春夏秋冬，换一生无怨无悔。 5

【考点】巧求周长【难度】2 星【题型】解答【解析】先想一想，减少的 6 厘米相当于正方形的几条边的边长呢？把两个正方形拼成一个长方形时，拼成的长方形的周长比原来两个正方形的 8 条边减少了 2 条边(如图所示) 而这两条边的和正好是减少的 6 厘米，所以，正方形的边长是 6 2 3   厘米，原来一个正方形的周长是 3 4 12 (厘米)   厘米．所以原来一个正方形的周长是： 6 2 4 12    【总结】通过这个例题，可以看出，求组合图形及一些特殊图形的周长与面积，一定要仔细观察，善于发现其中内在的联系，找出未知与已知的关系，将问题转化，从而得到解决．下面我们来学习几种求几何图形周长和面积的技巧．【答案】12 厘米【例 9】长方形 ABCD 长为 l0 厘米，宽为 4 厘米．E 是 BC 中点，四边形 ADCE 的周长比三角形 ABE 的周长多（）厘米．【考点】巧求周长【难度】2 星【题型】填空【关键词】走美杯，3 年级，初赛，第 14 题【解析】通过比较得出，四边形 ADCE 的周长比三角形 ABE 的周长多的是 AD 边，多 10 厘米。【答案】10 厘米【例 10】（第六届走美四年级初赛第 15 题）E 是正方形 ABCD 的边 CD 上的三等分点(如图)，BE 把正方形．分成一个梯形和一个三角形．梯形的周长比三角形的周长大 8 厘米．正方形 ABCD 的面积是 A B D E C 【解析】由 E 是正方形 ABCD 的边 CD 上的三等分点，知 DC=3EC，又有梯形的周长比三角形的周长大 8 【解析】厘米，知 4 份量是 8 厘米，1 份量是 2 厘米，则有正方形的边是 6 厘米，则正方形 ABCD 的面积是 36 【例 11】如图所示，一个大长方形被三条线段分成了四个小长方形，各条线段长度见图(单位：厘米)．求：图中所有长方形的周长之和．【考点】巧求周长【难度】3 星【题型】解答【解析】类似于上题，题目中所说的长方形，并不只包括最小的几个长方形，因此需要先求出每条线段在求和过程中被累加了多少次．因为没从大长方形的长上找到一条线段，就能对应地找到大长方形内的教师寄语：拼一个春夏秋冬，换一生无怨无悔。 6

一个长方形，所以可以利用上一个问题的结论来解决这个问题．当然，要考虑到，每个长方形都有两条长和两条宽，因此计算过程中应该注意不要漏算．先考虑大长方形的长上各边：应用上一道题目的结论，每条边上长为 4、3、1、2 的线段分别被计算了 4、6、6、4 次．然后再考虑大长方形的宽：因为共有 4 3 2 1 10 故总周长可以用下式计算得到：       个长方形，所以长度为 2 的宽被计算了10 2=20  4 4 3 6 1 6 2 4        （次）．厘米． 2   2 20 136     【答案】136 厘米【例 12】如图，从长方形纸片 ABCD 上剪去正方形 ADFE，剩下的长方形 EFCB 的周长是 100 厘米，则 AB 的长是厘米。【考点】巧求周长【难度】3 星【题型】填空【关键词】希望杯，4 年级，初赛， 15 题【解析】长方形的周长  2 【答案】 50 厘米  EF EB ，而 EF AE ，所以 AB=AE+EB=EF+FB=100÷2=50 厘米. 【例 13】如图，正方形 ABCD 的边长是 6 厘米，过正方形内的任意两点画直线，可把正方形分成 9 个小长方形。这 9 个小长方形的周长之和是厘米。【考点】巧求周长【难度】3 星【题型】填空【关键词】2006 年，第 4 届，希望杯，4 年级，初赛，13 题【解析】从总体考虑，在求这 9 个小长方形的周长之和时， AB 、 BC 、CD 、 DA 这四条边被用了1次，其余四条虚线被用了 2 次，所以 9 个小长方形的周长之和是： 6 4 6 2 4 72      （厘米）。【答案】 72 厘米【巩固】如图，正方形的边长为 4 ，被分割成如下12 个小长方形，求这12 个小长方形的所有周长之和．【考点】巧求周长【难度】3 星【题型】解答【解析】 4 4 4 5 2 56 【答案】 56      ．【巩固】有一个长方形纸片，长比宽多 2 厘米，周长是 36 厘米，用剪刀剪 3 下（如图），这 6 个长方形的周长之和是。教师寄语：拼一个春夏秋冬，换一生无怨无悔。 7

【考点】巧求周长【难度】3 星【题型】填空【关键词】学而思杯，3 年级，第 4 题【解析】根据题意知：长为： 18 2  ）   个宽，则周长和为： 36 4 10 2 8=92 2 10     （（厘米）。（厘米），宽为：18 10=8  （厘米），剪 3 刀后增加了 4 个长， 2 【答案】 92 厘米【例 14】如图，一个正方形被分割成 24 个互不重叠的小长方形，这 24 个小长方形的周长总和为 24 ，原正方形的面积是。【考点】巧求周长【难度】4 星【题型】填空【关键词】走美杯，5 年级，决赛，第 10 题，10 分【解析】由题目中的图可以看出，小长方形的周长和相当于正方形的 8 2 4    （条）边长，所以正方形面 20 积为    24 20 2     36 25 。【答案】 36 25 【例 15】如图，有一张长为 12 厘米，宽为 10 厘米的长方形纸片，按照虚线将这个纸片剪为两部分，这两部分的周长之和是_____________厘米．【考点】巧求周长【难度】3 星【题型】填空【关键词】中年级，决赛，4 题【解析】所求的周长之和＝原长方形的周长 2  虚线的总长度．原长方形的周长＝ (12 10) 2 虚线的总长度＝10 (12 3 4) 3 25   （厘米），则所求周长之和＝ 44 2 25 94        （厘米），   （厘米）． 44 【答案】 94 厘米【例 16】将若干个边长为1 的正六边形(即单位六边形)拼接起来，得到一个拼接图形，如图：教师寄语：拼一个春夏秋冬，换一生无怨无悔。 8

分享到：

赞收藏

资料库

4-2-2 巧求周长.教师版.doc

相关推荐

小学奥数

热门标签

最新资料