7-6-3 计数之对应法.学生版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：0.82M 资料格式：doc 举报版权申诉

第1页 / 共7页

第2页 / 共7页

第3页 / 共7页

第4页 / 共7页

第5页 / 共7页

第6页 / 共7页

第7页 / 共7页

文本预览

7-6-3 计数之对应法教学目标前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法，比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等，这里再集中学习一下计数中其他常见的方法，主要有归纳法、整体法、对应法、递推法．对这些计数方法与技巧要做到灵活运用．例题精讲将难以计数的数量与某种可计量的事物联系起来，只要能建立一一对应的关系，那么这两种事物在数量上是相同的．事实上插入法和插板法都是对应法的一种表现形式．模块一、图形中的对应关系【例 1】在 8×8 的方格棋盘中，取出一个由三个小方格组成的“L”形（如图），一共有多少种不同的方法？【考点】计数之图形中的对应关系【难度】3 星【题型】解答【解析】注意：数“不规则几何图形”的个数时，常用对应法．第 1 步：找对应图形每一种取法，有一个点与之对应，这就是图中的 A 点，它是棋盘上横线与竖线的交点，且不在棋盘边上．第 2 步：明确对应关系从下图可以看出，棋盘内的每一个点对应着 4 个不同的取法（“L”形的“角” 在 2×2 正方形的不同“角”上）．第 3 步：计算对应图形个数由于在 8×8 的棋盘上，内部有 7×7=49（个）交叉点，第 4 步：按照对应关系，给出答案故不同的取法共有 49×4=196（种）．评注:通过上面两个范例我们知道,当直接去求一个集合元素的个数较为困难的时候,可考虑采用相等的原则,把问题转化成求另一个集合的元素个数．【答案】196 【例 2】在 8×8 的黑白相间染色的国际象棋棋盘中，以网格线为边的、恰包含两个白色小方格与一个黑色小方格的长方形共有多少个？【考点】计数之图形中的对应关系【难度】3 星【题型】解答【解析】首先可以知道题中所讲的1 3 长方形中间的那个小主格为黑色，这是因为两个白格不相邻，所以不能在中间．显然，位于棋盘角上的黑色方格不可能被包含在这样的长方形中．下面分两种情况来分 7-6-3.计数之对应法.题库教师版 page 1 of 7

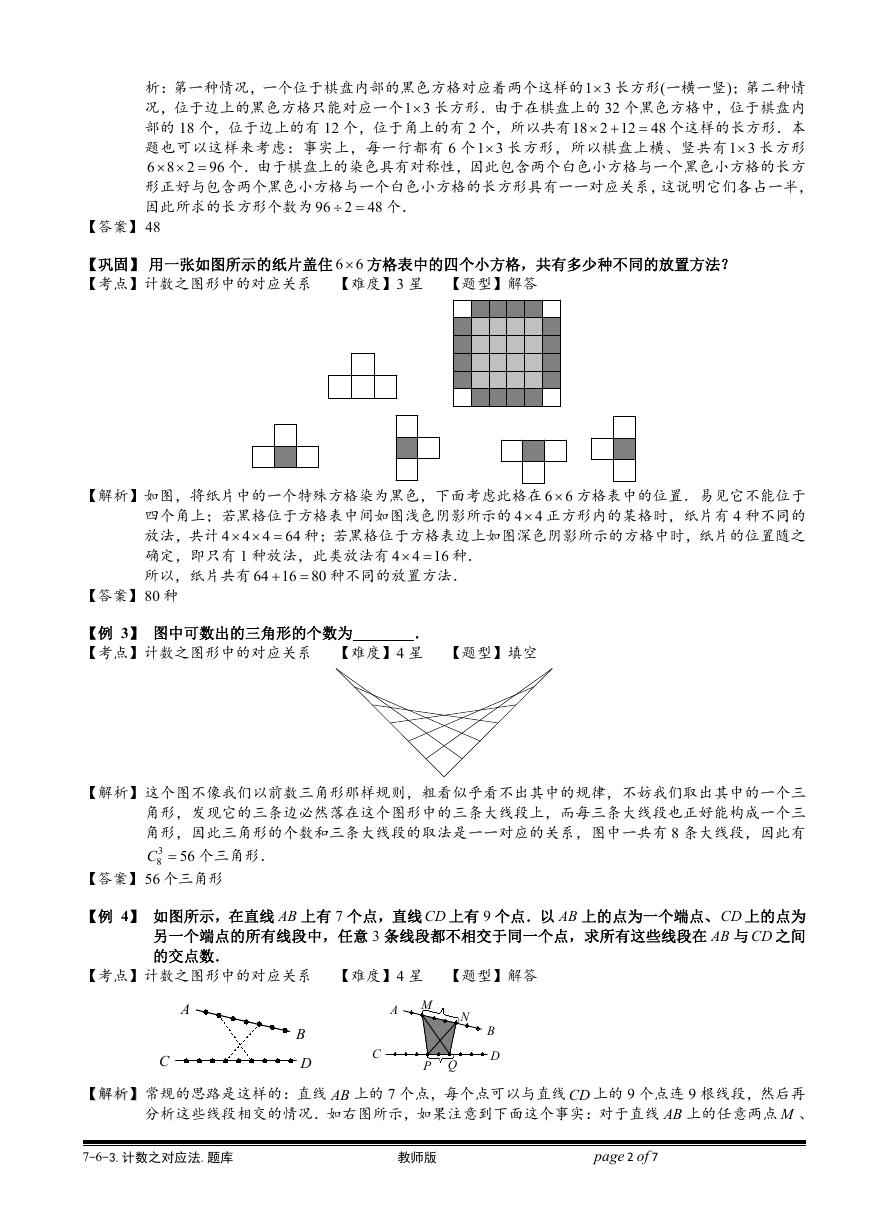
析：第一种情况，一个位于棋盘内部的黑色方格对应着两个这样的1 3 长方形(一横一竖)；第二种情况，位于边上的黑色方格只能对应一个1 3 长方形．由于在棋盘上的 32 个黑色方格中，位于棋盘内部的 18 个，位于边上的有 12 个，位于角上的有 2 个，所以共有18 2 12  个这样的长方形．本题也可以这样来考虑：事实上，每一行都有 6 个1 3 长方形，所以棋盘上横、竖共有1 3 长方形 6 8 2 96    个．由于棋盘上的染色具有对称性，因此包含两个白色小方格与一个黑色小方格的长方形正好与包含两个黑色小方格与一个白色小方格的长方形具有一一对应关系，这说明它们各占一半，因此所求的长方形个数为 96 2   个．   48 48 【答案】 48 【巩固】用一张如图所示的纸片盖住 6 6 方格表中的四个小方格，共有多少种不同的放置方法？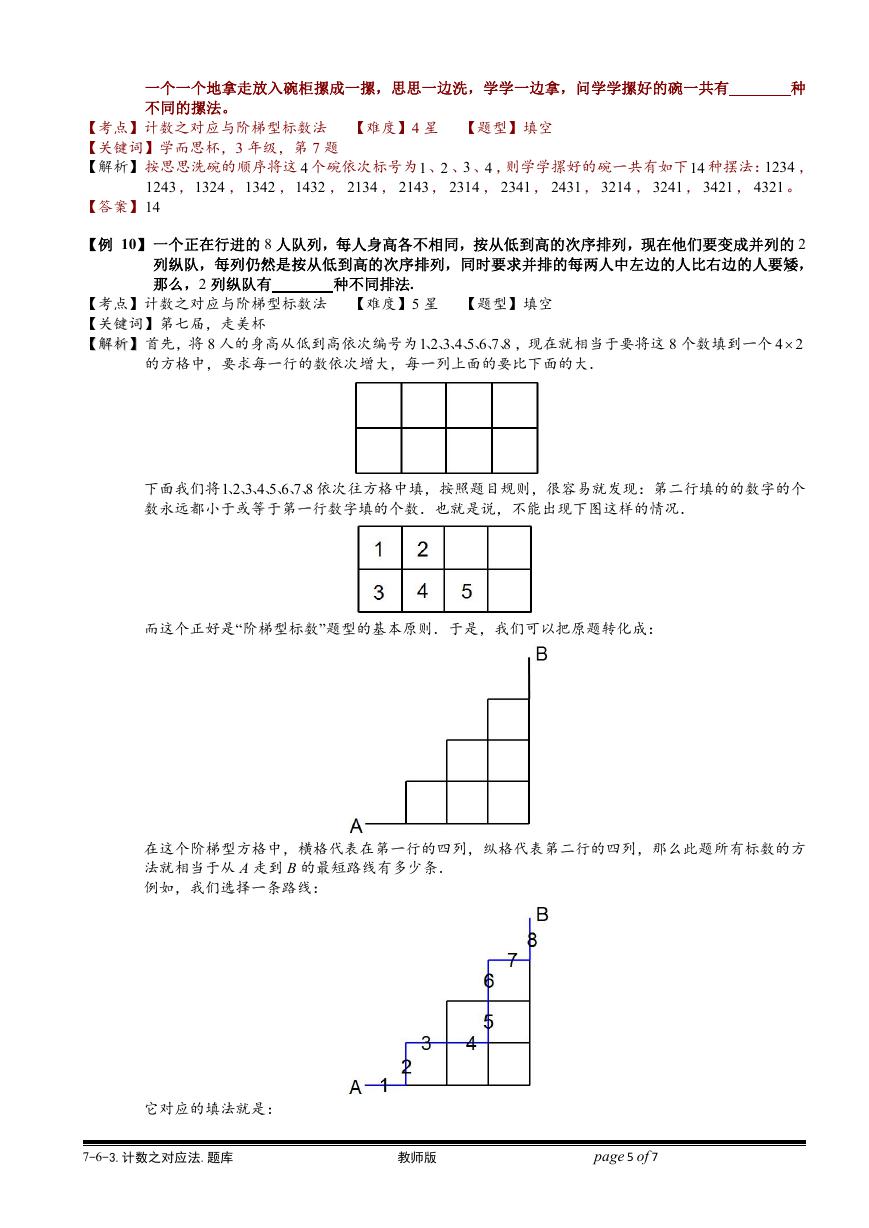【考点】计数之图形中的对应关系【难度】3 星【题型】解答【解析】如图，将纸片中的一个特殊方格染为黑色，下面考虑此格在 6 6 方格表中的位置．易见它不能位于四个角上；若黑格位于方格表中间如图浅色阴影所示的 4 4 正方形内的某格时，纸片有 4 种不同的放法，共计 4 4 4 64    种；若黑格位于方格表边上如图深色阴影所示的方格中时，纸片的位置随之确定，即只有 1 种放法，此类放法有 4 4 16 所以，纸片共有 64 16 80  种不同的放置方法．   种．  【答案】80 种【例 3】图中可数出的三角形的个数为【考点】计数之图形中的对应关系【难度】4 星【题型】填空．【解析】这个图不像我们以前数三角形那样规则，粗看似乎看不出其中的规律，不妨我们取出其中的一个三角形，发现它的三条边必然落在这个图形中的三条大线段上，而每三条大线段也正好能构成一个三角形，因此三角形的个数和三条大线段的取法是一一对应的关系，图中一共有 8 条大线段，因此有 3 C  个三角形． 8 56 【答案】 56 个三角形【例 4】如图所示，在直线 AB 上有 7 个点，直线 CD 上有 9 个点．以 AB 上的点为一个端点、CD 上的点为另一个端点的所有线段中，任意 3 条线段都不相交于同一个点，求所有这些线段在 AB 与 CD 之间的交点数．【考点】计数之图形中的对应关系【难度】4 星【题型】解答 A C A M N C P Q B D B D 【解析】常规的思路是这样的：直线 AB 上的 7 个点，每个点可以与直线 CD 上的 9 个点连 9 根线段，然后再【解析】分析这些线段相交的情况．如右图所示，如果注意到下面这个事实：对于直线 AB 上的任意两点 M 、 7-6-3.计数之对应法.题库教师版 page 2 of 7

N 与直线 CD 上的任意两点 P 、Q 都可以构成一个四边形 MNQP ，而这个四边形的两条对角线 MQ 、 NP 的交点恰好是我们要计数的点，同时，对于任意四点( AB 与 CD 上任意两点)都可以产生一个这样的交点，所以图中两条线段的交点与四边形有一一对应的关系．这说明，为了计数出有多少个交点，我们只需要求出在直线 AB 与 CD 中有多少个满足条件的四边形 MNQP 就可以了！从而把问题转化为：在直线 AB 上有 7 个点，直线 CD 上有 9 个点．四边形 MNQP 有多少个？其中点 M 、 N 位于直线 AB 上，点 P 、 Q 位于直线 CD 上．这是一个常规的组合计数问题，可以用乘法原理进行计算：由于线段 MN 有 2 C  种选择方式，线段 PQ 有 2 C  种选择方式，根据乘法原理，共可产生 9 7 21 36 756  个四边形．因此在直线 AB 与 CD 之间共有 756 个交点． 36 21  【答案】 756 个交点模块二、数字问题中的对应关系【例 5】有多少个四位数，满足个位上的数字比千位数字大，千位数字比百位大，百位数字比十位数字大？【考点】计数之数字问题中的对应关系【难度】4 星【题型】解答【解析】由于四位数的四个数位上的数的大小关系已经非常明确，而对于从 0～9 中任意选取的 4 个数字，它【解析】们的大小关系也是明确的，那么由这 4 个数字只能组成 1 个符合条件的四位数(题目中要求千位比百位大，所以千位不能为 0，本身已符合四位数的首位不能为 0 的要求，所以进行选择时可以把 0 包含在内)，也就是说满足条件的四位数的个数与从 0～9 中选取 4 个数字的选法是一一对应的关系，那么满足条件的四位数有 4 C 10 个． 210   10 9 8 7    4 3 2 1    【答案】 210 个【巩固】三位数中，百位数比十位数大，十位数比个位数大的数有多少个？【考点】计数之数字问题中的对应关系【难度】4 星【题型】解答【解析】相当于在 10 个数字中选出 3 个数字，然后按从大到小排列.共有 10×9×8÷（3×2×1）=120 种．实际上，前铺中每一种划法都对应着一个数．【答案】120 种【例 6】数 3 可以用 4 种方法表示为一个或几个正整数的和，如 3，1 2 ， 2 1 ，1 1 1   ．问：1999 表示为一个或几个正整数的和的方法有多少种？【考点】计数之数字问题中的对应关系【难度】4 星【题型】解答【解析】我们将 1999 个 1 写成一行，它们之间留有 1998 个空隙，在这些空隙处，或者什么都不填，或者填【解析】上“＋”号．例如对于数 3，上述 4 种和的表达方法对应：1 1 1，1  1 1，1 1  1，1  1  1．可见，将 1999 表示成和的形式与填写 1998 个空隙处的方式之间是一一对应的关系，而每一个空隙处都有填 “ ＋ ” 号和不填 “ ＋ ” 号 2 种可能，因此 1999 可以表示为正整数之和的不同方法有 2 2 2     1998 1998 2 种．个相乘 2 【答案】 19982 种【例 7】请问至少出现一个数码 3，并且是 3 的倍数的五位数共有多少个？【考点】计数之数字问题中的对应关系【难度】4 星【题型】解答【关键词】小学数学竞赛【解析】五位数共有 90000 个，其中 3 的倍数有 30000 个．可以采用排除法，首先考虑有多少个五位数是 3 【解析】的倍数但不含有数码 3.首位数码有 8 种选择，第二、三、四位数码都有 9 种选择．当前四位的数码确定后，如果它们的和除以余数为 0，则第五位数码可以为 0、6、9；如果余数为 1，则第五位数码可以为 2、5、8；如果余数为 2，则第五位数码可以为 1、4、7.可见只要前四位数码确定了，第五位数码都有 3 种选择，所以五位数中是 3 的倍数但不含有数码 3 的数共有 8 9 9 9 3 17496 所以满足条件的五位数共有 30000 17496 12504      个．个．   【答案】12504 个模块三、对应与阶梯型标数法【例 8】游乐园的门票 1 元 1 张，每人限购 1 张．现在有 10 个小朋友排队购票，其中 5 个小朋友只有 1 元 7-6-3.计数之对应法.题库教师版 page 3 of 7

的钞票，另外 5 个小朋友只有 2 元的钞票，售票员没有准备零钱．问有多少种排队方法，使售票员总能找得开零钱？【考点】计数之对应与阶梯型标数法【难度】5 星【题型】解答【解析】与类似题目找对应关系．要保证售票员总能找得开零钱，必须保证每一位拿 2 元钱的小朋友前面的【解析】若干小朋友中，拿 1 元的要比拿 2 元的人数多，先将拿 1 元钱的小朋友看成是相同的，将拿 2 元钱的小朋友看成是相同的，可以利用斜直角三角模型．在下图中，每条小横线段代表 1 元钱的小朋友，每条小竖线段代表 2 元钱的小朋友，因为从 A 点沿格线走到 B 点，每次只能向右或向上走，无论到途中哪一点，只要不超过斜线，那么经过的小横线段都不少于小竖线段，所以本题相当于求下图中从 A 到 B 有多少种不同走法．使用标数法，可求出从 A 到 B 有 42 种走法． B 42 42 28 14 5 1 14 14 9 4 1 5 5 3 1 2 2 1 1 1 1 A 但是由于 10 个小朋友互不相同，必须将他们排队，可以分成两步，第一步排拿 2 元的小朋友，5 个人共有 5 种排队方法．这样，使售票员能找得开零钱的排队方法共有 42 14400 604800 种排法；第二步排拿到 1 元的小朋友，也有 120 种排法，所以共有 5 (种)． 14400  ！！ 5 ！ 120 【答案】 604800 种   【例 9】学学和思思一起洗 5 个互不相同的碗（顺序固定），思思洗好的碗一个一个往上摞，学学再从最上面一个一个地拿走放入碗柜摞成一摞，思思一边洗，学学一边拿，那么学学摞好的碗一共有种不同的摞法．【考点】计数之对应与阶梯型标数法【难度】5 星【题型】解答【关键词】学而思杯，5 年级，第 7 题【解析】方法一：如下所示，共有 42 种不同的摞法：     ，3 5 4 2 1     ，5 2 4 3 1     ，5 4 3 1 2     ，4 5 1 3 2     ，1 3 5 4 2     ，1 4 5 2 3     ，1 2 5 3 4     ，5 3 4 2 1     ，2 4 5 3 1     ，4 5 3 1 2     ，1 5 4 3 2     ，1 3 4 5 2     ，1 2 5 4 3     ，1 5 2 3 4     ，4 5 3 2 1 5 4 3 2 1 4 5 2 3 1     ，2 5 4 3 1 2 3 5 4 1     ，2 3 4 5 1     ，5 4 1 3 2 3 4 5 1 2 5 1 3 4 2     ，1 5 3 4 2 1 5 4 2 3     ，5 1 4 2 3 1 2 4 5 3     ，1 2 3 5 4     ，5 4 2 3 1     ，     ，2 5 3 4 1     ，     ，3 5 4 1 2     ，     ，1 4 5 3 2     ，     ，4 5 1 2 3     ，     ，1 5 2 4 3     ，     ，1 2 3 4 5     。方法二：我们把学学洗的 5 个碗过程看成从起点向右走 5 步（即洗几个碗就代表向右走几步），思思拿 5 个碗的过程看成是向上走 5 步（即拿几个碗就代表向上走几步），摞好碗的摞法，就代表向右、向上走 5 步到达终点最短路线的方法.由于洗的碗要多余拿的碗，所以向右走的路线要多余向上走的路线，所以我们用下面的斜三角形进行标数，共有 42 种走法，所以共有 42 种不同的摞法。     ，3 4 5 2 1     ，5 2 3 4 1     ，5 3 4 1 2     ，5 1 4 3 2     ，5 4 1 2 3     ，5 1 2 4 3     ，5 1 2 3 4 【答案】 42 种【巩固】学学和思思一起洗 4 个互不相同的碗（顺序固定），思思洗好的碗一个一个往上摞，学学再从最上面 7-6-3.计数之对应法.题库教师版 page 4 of 7

一个一个地拿走放入碗柜摞成一摞，思思一边洗，学学一边拿，问学学摞好的碗一共有不同的摞法。种【考点】计数之对应与阶梯型标数法【难度】4 星【题型】填空【关键词】学而思杯，3 年级，第 7 题【解析】按思思洗碗的顺序将这 4 个碗依次标号为1、2 、3 、4 ，则学学摞好的碗一共有如下14 种摆法：1234 ， 1243 ，1324 ，1342 ，1432 ， 2134 ， 2143 ， 2314 ， 2341 ， 2431 ， 3214 ， 3241 ， 3421 ， 4321 。【答案】14 【例 10】一个正在行进的 8 人队列，每人身高各不相同，按从低到高的次序排列，现在他们要变成并列的 2 列纵队，每列仍然是按从低到高的次序排列，同时要求并排的每两人中左边的人比右边的人要矮，那么，2 列纵队有种不同排法. 【考点】计数之对应与阶梯型标数法【难度】5 星【题型】填空【关键词】第七届，走美杯【解析】首先，将 8 人的身高从低到高依次编号为1 2 3 4 5 6 7 8 【解析】、、、、、、、，现在就相当于要将这 8 个数填到一个 4 2 的方格中，要求每一行的数依次增大，每一列上面的要比下面的大．下面我们将1 2 3 4 5 6 7 8 数永远都小于或等于第一行数字填的个数．也就是说，不能出现下图这样的情况．、、、、、、、依次往方格中填，按照题目规则，很容易就发现：第二行填的的数字的个而这个正好是“阶梯型标数”题型的基本原则．于是，我们可以把原题转化成：在这个阶梯型方格中，横格代表在第一行的四列，纵格代表第二行的四列，那么此题所有标数的方法就相当于从 A 走到 B 的最短路线有多少条．例如，我们选择一条路线：它对应的填法就是： 7-6-3.计数之对应法.题库教师版 page 5 of 7

最后，用“标数法”得出从 A 到 B 的最短路径有 14 种，如下图：．【答案】14 种【巩固】将 1~12 这 12 个数填入到 2 行 6 列的方格表中，使得每行右边比左边的大，每一列上面比下面的大，共有多少种填法？【考点】计数之对应与阶梯型标数法【难度】5 星【题型】解答【解析】根据对应关系，再运用阶梯型标数法画图如下：【解析】 132 42 42 28 14 5 132 90 48 20 6 14 14 9 4 5 5 3 2 2 1 1 1 1 1 1 1 1 共有 132 种填法．【答案】132 种【例 11】在一次小组长选举中，铮铮与昊昊两人作为候选人参加竞选，一共得了 7 张选票。在将 7 张选票种不同的情况。逐一唱票的过程中，昊昊的得票始终没有超过铮铮。那么这样的唱票过程有【考点】计数之对应与阶梯型标数法【难度】5 星【题型】填空【关键词】学而思杯，6 年级，1 试，第 14 题【解析】标数法（1）7 张全是铮铮，1 种；（2）6 张铮铮,1 张昊昊,6 种；（3）5 张铮铮,2 张昊昊,14 种；（4）4 张铮铮,3 张昊昊,14 种。一共 35 种。【答案】 35 种模块四、不完全对应关系【例 12】圆周上有 12 个点，其中一个点涂红，还有一个点涂了蓝色，其余 10 个点没有涂色，以这些点为顶 7-6-3.计数之对应法.题库教师版 page 6 of 7

点的凸多边形中，其顶点包含了红点及蓝点的多边形称为双色多边形；只包含红点(蓝点)的多边形称为红色(蓝色)多边形．不包含红点及蓝点的称无色多边形．试问，以这 12 个点为顶点的所有凸多边形(边数可以从三角形到 12 边形)中，双色多边形的个数与无色多边形的个数，哪一种较多？多多少个？【考点】计数之不完全对应关系【难度】4 星【题型】解答【解析】从任意一个双色的 N 边形出发( 【解析】 5N  时)，在去掉这个双色多边形中的红色顶点与蓝色顶点后，将得到一个无色的 2N  边形；另一方面，对于一个任意的无色的 M 边形，如果加上红色顶点和蓝色顶 2M  边形，所以无色多边形与双色多边形中的五边形以上的图形是一一对点，就得到一个双色的应的关系，所以双色多边形的个数比较多，多的是双色三角形和双色四边形的个数．而双色三角形有 10 个，双色四边形有 2 C  个，所以双色多边形比无色多边形多10 45 55 10  个．  【答案】双色多边形比无色多边形多10 45 55  个 45  【例 13】有一类各位数字各不相同的五位数 M ，它的千位数字比左右两个数字大，十位数字也比左右两位数字大．另有一类各位数字各不相同的五位数W ，它的千位数字比左右两个数字小，十位数字也比左右两位数字小．请问符合要求的数 M 与W ，哪一类的个数多？多多少？【考点】计数之不完全对应关系【难度】5 星【题型】解答【解析】 M 与W 都是五位数，都有千位和十位与其它数位的大小关系，所以两类数有一定的对应关系．比如【解析】 ( A 不为 0) ，那么就有一个与之相反并对应的五位数 1      1  E  C B D … )(9 )(9 )(9  ) )(9 A 3 3n   的符合要求的数．  必属于 4 类，比如13254 为 M 类，则与之对应的 86754 为W 类．有一个符合要求的五位数 M ABCDE (9 所以对于 M 类的每一个数， 1n  类都有一个数与之对应．但是两类数的个数不是一样多，因为 M 类中 0 不能做首位，而W 类中 9 可以做首位．所以W 类的数比 M 类的数要多，多的就是就是首位为 a n  3 3 a    n 3 1 n  ( 个 ) a  的W 类的数的个数，首先要确定另外四个数，因为要求各不相同，从除 9 外的其计算首位为 1 它 9 个数字中选出 4 个，有 4 C  种选法． 9 对于每一种选法选出来的 4 个数，假设其大小关系为 5 ，由于其中最小的数只能在千位和十位上，最大的数只能在百位和个位上，所以符合要求的数有 60 类：①千位、十位排 1A 、 2A ，有两种方法，百位、十位排 3A 、 4A ，也有两种方法，故此时共有 3 种；②千位、十位排 0 、 3A ，只能是千位 3A ，百位 4A ，十位 3 ，个位 6 ，只有 3 种方法．根据乘法原理，首位为 9 的W 类的数有 126  个． 4 1  630 126    0 【答案】W 多，多 630 个【例 14】用 1 元，2 元，5 元，10 元四种面值的纸币若干张(不一定要求每种都有)，组成 99 元有 P 种方法，组成 101 元有 Q 种方法，则 Q P  ．【考点】计数之不完全对应关系【难度】5 星【题型】填空【关键词】学而思杯，6 年级，1 试【解析】如果10 元的取 0 张，即 0 【解析】 z  ，则 21 2 z 如果10 元的取1张，即 1z  ，则 21 2 z 如果10 元的取 2 张，即 2 z  ，则 21 2 z  ，即 5 元的有 21 种取法； 21 19  ，即 5 元的有19 种取法； 17  ，即 5 元的有17 种取法；  如果10 元的取10 张，即 10 1 11   所以总数为 z  ，则 21 2 1z 121  21 19 17     2 ，那么 Q P  。 121  ，即 5 元的有1种取法；【答案】121 7-6-3.计数之对应法.题库教师版 page 7 of 7

分享到：

赞收藏

资料库

7-6-3 计数之对应法.学生版.doc

相关推荐

小学奥数

热门标签

最新资料