5-1-2-2 乘除法数字谜（一）.教师版.doc-资料库

第1页 / 共12页

第2页 / 共12页

第3页 / 共12页

第4页 / 共12页

第5页 / 共12页

第6页 / 共12页

第7页 / 共12页

第8页 / 共12页

5-1-2-2.乘除法数字谜（一）教学目标数字谜是杯赛中非常重要的一块，特别是迎春杯，数字谜是必考的，一般学生在做数字谜的时候都采用尝试的方式，但是这样会在考试中浪费很多时间．本模块主要讲乘除竖式数字谜的解题方法，学会通过找突破口来解决问题．最后通过例题的学习，总结解数字谜问题的关键是找到合适的解题突破口．在确定各数位上的数字时，首先要对填写的数字进行估算，这样可以缩小取值范围，然后再逐一检验，去掉不符合题意的取值，直到取得正确的解答．知识点拨 1. 数字谜定义:一般是指那些含有未知数字或未知运算符号的算式． 2. 数字谜突破口：这种不完整的算式，就像“谜”一样，要解开这样的谜，就得根据有关的运算法则，数的性质（和差积商的位数，数的整除性，奇偶性，尾数规律等）来进行正确的推理，判断． 3. 解数字谜：一般是从某个数的首位或末位数字上寻找突破口．推理时应注意： ⑴ 数字谜中的文字，字母或其它符号，只取 0 ~ 9 中的某个数字； ⑵ 要认真分析算式中所包含的数量关系，找出尽可能多的隐蔽条件； ⑶ 必要时应采用枚举和筛选相结合的方法（试验法），逐步淘汰掉那些不符合题意的数字； ⑷ 数字谜解出之后，最好验算一遍．例题精讲模块一、乘法数字谜【例 1】下面是一个乘法算式：问：当乘积最大时，所填的四个数字的和是多少？【考点】乘法数字谜【难度】1 星【题型】填空【关键词】华杯赛，初赛，第 2 题【解析】乘积是两位数并且是 5 的倍数，因而最大是 95.95÷5＝19，所以题中的算式实际上是所以，所填四个数字之和便是 1＋9＋9＋5＝24 【答案】 24 5-1-2-2.乘除法数字谜（一）.题库教师版 page 1 of 12

【例 2】下面两个算式中，相同的汉字代表相同的数字，不同的汉字代表不同的数字．  美妙数学数数妙，  美+妙数学=妙数数。美妙数学 ___________ 【难度】2 星【题型】填空  【考点】乘法数字谜【关键词】走美杯，四年级，初赛，第 12 题，五年级，初赛，第 11 题【解析】由   美妙数学数数妙知，“美”不为 1，且“美”×“妙”<10，如果“美”为 2，根据“美”×“学”的个位数为 “妙”，那么“妙”为偶数，即为 4，推出“学”为 7，又由 “美”+“学”=“数”，可知“数”为 9，所以美妙数学 2497。  【答案】 2497 【例 3】北京有一家餐馆，店号“天然居”，里面有一副著名对联：客上天然居，居然天上客。巧的很，这副对联恰好能构成一个乘法算式(见右上式)。相同的汉字代表相同的数字，不同的汉字代表不同的数字。“天然居”表示成三位数是_______。【难度】2 星【题型】填空【考点】乘法数字谜【关键词】走美杯，4 年级，决赛，第 6 题，10 分【解析】因为竖式中五位数乘 4 仍是五位数，所以“客”是人于 0 小于 3 的偶数，只能是 2，并推知“居” 8。因为“上”乘 4 不向上进位，且是奇数，所以“上”  1，并推知“然”  7。则所表示的三位数是 978。【答案】 978 【例 4】下面算式(1)是一个残缺的乘法竖式，其中□≠2，那么乘积是多少？【考点】乘法数字谜【解析】如式(2)，由题意 a≠2，所以 b≥6，从而 d≥6．由 22□÷c≥60 和 c＞2 知 c=3，所以 22□是 225 或 228， 75 【解析】 de  ．再由乘积不小于 30000 和所有的□≠2，推出唯一的解【难度】2 星【题型】填空 de  76 或 76．因为 75×399＜30 000，所以 76×396=30096．【答案】76×396=30096 【例 5】下面残缺的算式中，只写出了 3 个数字 1，其余的数字都不是 1，那么这个算式的乘积是？【考点】乘法数字谜【难度】2 星【题型】填空【解析】为了说明的方便，这个算式中的关键数字用英文字母表示．很明显 e= 0．从 c ab 的个位数是 1，b 【解析】可能是 3，7，9 三数之一，两位数 ab 应是（100+f）的因数．101，103，107，109 是质数，f=0 或 5 也明显不行．102=17×6，则 ab =17，C 只能取 3， 13 ab  ，   是三位数；108=27×4， c 可取 7，c × ab =7×13，仍不是三位数；106=53×2， 53 则 ab =27，c 是 3．因此这个乘法算式是 53×72=3816，故这个算式的乘积是 3816。   ，不是三位数；104=13×8,则 c ab ab  ，c=7，   ，不是三位数． 7 53 3 27 c ab c ab 3 17 5-1-2-2.乘除法数字谜（一）.题库教师版 page 2 of 12

【答案】3816 = 【例 6】右面的算式中，每个汉字代表一个数字（0~9），不同汉字代表不同数字．美+妙+数+学+花+园．  4 5 美妙数学花园数学真美妙 2 好好好美妙 3 8 0 【考点】乘法数字谜【难度】3 星【题型】填空【关键词】走美杯，3 年级，决赛，第 5 题，10 分【解析】从式中可以看出“花” “学”的乘积末位为零，故“花”与“学”之中必有一个为数字 0 或 5 ，当 “学”是 0 时，由下面一列中的“学”、“ 3 ”，“好”，知“好”为“ 3 ”或“ 4 ”，则“数”取 0 ~ 9 中的任何一个数字也不行，同样地“学”也不是 5 ，而“花”不能是 0 ，所以“花”为数字 5 ，则可以．故“美” 8 ，“妙” 4 ，“数” 7 “学” 6 ．再看下逆向计算出：美妙数学 42380 5 8476 面的加法：“数” 2  “好”且进1位，可知必有进位且“好” 0 ，于是“真” 2 ，所以再次逆推 “ 园 ” 76284 8476 9  ．符合题意，假设成立，故，美  妙  数  学  花  园        ． 8 4 7 6 5 9 36      【答案】 36 【例 7】在右边的乘法算式中，字母 A 、B 和 C 分别代表一个不同的数字，每个空格代表一个非零数字．求 A 、 B 和 C 分别代表什么数字？  A B C A B C 9 4 1 【考点】乘法数字谜【难度】3 星【题型】填空【解析】第一个部分积中的 9 是 C C 的个位数字，所以 C 要么是 3 ，要么是 7 ．如果 3C  ，第二个部分积中的 4 是积 3 B 的个位数字，所以 8B  ．同理，第三个部分积中的1 是积 3 B 的个位数字，因此 7A  ．检验可知 7A  ， 8B  ， 3C  满足题意．如果 7C  ，类似地可知 2B  ， 3A  ，但这时第二个部分积 327 2 不是四位数，不合题意．所以 A 、 B 和 C 代表的数字分别是 7、8、3. 【答案】7、8、3 【例 8】在每个方框中填入一个数字，使得乘法竖式成立．已知乘积有两种不同的得数，那么这两个得数的差是．【考点】乘法数字谜【难度】3 星【题型】填空【关键词】迎春杯，高年级，复试，5 题【解析】A 与乘数的乘积比 2 与乘数的乘积小，所以 1A ， 1C ，又 B 与 2 的乘积个位是 0，所以 0 【解析】 6C 不进位，那么 6D 个位是 0，得 5D ，两个乘法式子分别为 515 216 为 (515 510) 216 1080 ．     和 510 216 5或B ，  ，乘积的差 5-1-2-2.乘除法数字谜（一）.题库教师版 page 3 of 12

【答案】1080 【例 9】在图中的每个方框中填入一个适当的数字，使得乘法竖式成立。乘积等于。  2 0 0 8 【难度】3 星【题型】填空【考点】乘法数字谜【关键词】走美杯，5 年级，决赛，第 6 题，10 分【解析】根据乘法算式，被乘数乘以 2 后得到一个 3 位数，且此三位数的最高位在最终的运算中进位了，所以被乘数的最高位应该是 4 ，而乘数的十位数乘以被乘数后得到的结果也是三位数，所以乘数的十位数只能是1或 2 ，如果是1，那么被乘数的十位数肯定是 0 ，第三位数字必为 4 ，但此时 404 21 不可能是 6 位数，故乘数第二位必为 2 ，被乘数第三位必为 4 ，被乘数第二位为 5 或 0 ，假设被乘数第二位是 0 ，则 404 22 。不可能是六位数，所以被乘数必然是 454 ，经试算，乘式为 454 229 103966   【答案】103966 【例 10】如图，请在右图每个方框中填入一个数字，使乘法竖式成立。 2 0 × 0 7 【考点】乘法数字谜【难度】3 星【题型】填空【关键词】走美杯，初赛，六年级，第 7 题 1 5 3 0 0 3 4 2 8 5 2 0 8 8 8 × 3 7 0 7 8 【解析】【解析】【答案】 5-1-2-2.乘除法数字谜（一）.题库教师版 page 4 of 12

1 5 3 0 0 3 4 2 8 5 2 0 8 8 8 × 3 7 0 7 8 【例 11】在下面的乘法算式中，相同的字母表示相同的数字，不同的字母表示不同的数字．则 A  ， ABCDE 表示的五位数是．  6 A A C A A A E B 8 D D 【考点】乘法数字谜【难度】3 星【题型】填空【关键词】学而思杯，5 年级，第 13 题【解析】 2A  , 【答案】 2A  , ABCDE  ABCDE  23147 23147 【例 12】如图，请在右图每个方框中填入一个不是 8 的数字，使乘法竖式成立。 8 × 8 8 8 8 【考点】乘法数字谜【难度】4 星【题型】填空【关键词】走美杯，四年级，第 11 题【解析】【答案】 5-1-2-2.乘除法数字谜（一）.题库教师版 page 5 of 12

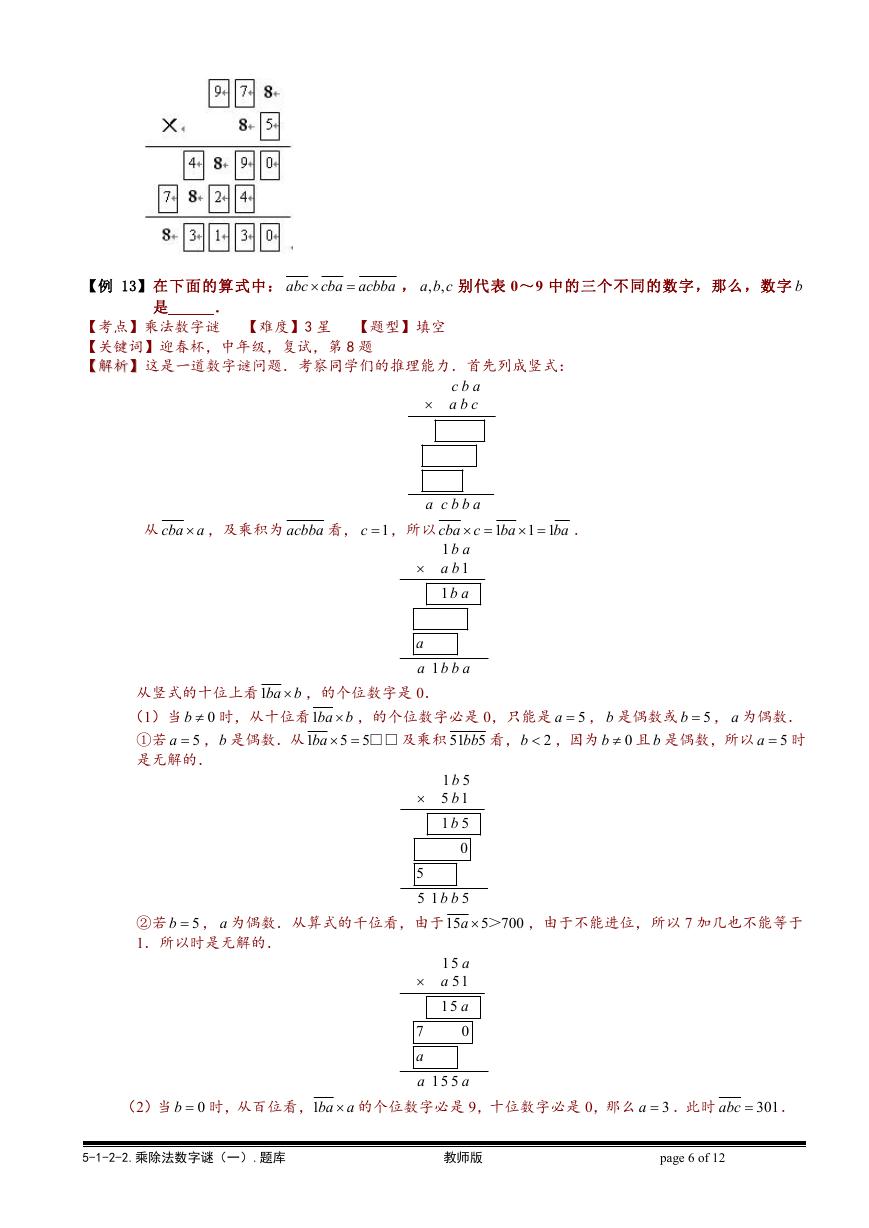
【例 13】在下面的算式中： abc cba   acbba ， , ,a b c 别代表 0～9 中的三个不同的数字，那么，数字 b 是．【考点】乘法数字谜【难度】3 星【题型】填空【关键词】迎春杯，中年级，复试，第 8 题【解析】这是一道数字谜问题．考察同学们的推理能力．首先列成竖式：【解析】 c b a a b c  从  cba a ，及乘积为 acbba 看， 1c ，所以   1 ba 1 1   ba ． a c b b a cba c 1 b a 1 a b 1 b a  a a 1 从竖式的十位上看1 ba b ，的个位数字是 0．（1）当 0b 时，从十位看1 ba b ，的个位数字必是 0，只能是 5a ， b 是偶数或 5b ， a 为偶数． ①若 5a ，b 是偶数．从1 及乘积 51 5bb 看， 2b ，因为 0b 且 b 是偶数，所以 5a 时是无解的． 5 5□□ b b a ba    1 5 b 5 1 b 1 5 b 0 b b ②若 5b ， a 为偶数．从算式的千位看，由于15 1．所以时是无解的． 5 5 700＞a ，由于不能进位，所以 7 加几也不能等于 5 5 1  7 a a 15 a 51 a 15 a 0 15 5 a （2）当 0b 时，从百位看，1 ba a 的个位数字必是 9，十位数字必是 0，那么 3a ．此时 abc  301 ． 5-1-2-2.乘除法数字谜（一）.题库教师版 page 6 of 12

10 a 01 a 10 a 10 0 a  a a 【答案】301 【例 14】如图所示的乘法竖式中，“学而思杯”分别代表 0～9 中的一个数字，相同的汉字代表相同的数字，不同的汉字代表不同的数字，那么“学而思杯”代表的数字分别为________  学而思杯学而思杯【考点】乘法数字谜【难度】3 星【题型】填空【解析】首先从式子中可以看出“思” 0 ，另外第三个部分积的首位只能为 9，所以“学”只能为 3．由于 3 个部分积都是四位数，而且第三个部分积的首位为 9，所以它比其它两个部分积要大，从而“学”比“而” 和“杯”都大，所以“而”和“杯”只能分别为 1 和 2，这样“学而思杯”就可能为 3102 或 3201．分别进行符合，所以“学而思杯” 检验，发现 3102 3102 9622404 代表的数字分别为 3、2、0、1．，与算式不相符，而 3201 3201 10246401     【答案】3、2、0、1 模块二、除法数字谜【例 15】在方格内填上适当的数字，使得除法竖式成立。【考点】除法数字谜【难度】3 星【题型】填空【关键词】走美杯，决赛，5 年级，决赛，第 9 题，10 分【解析】20047-13=20034  2×3 3 ×7×53。由商的个位是 2 知，除数乘以 2 的个位是 4，所以除数的个位是 2 或 7。因为 20034 只有一个因子 2，所以 20034 只能分解成一个偶数与一个奇数的乘积，由商是偶数推知除数是奇数，所以除数的个位是 7。20034 的两位数因数中只有 3 3 =27 符合要求，所以除数是 27，商是 20034÷27  742。 13 【答案】 20047 27=742   【例 16】如图所示的除法算式中，每个 □ 各代表一个数字，则被除数是。 5-1-2-2.乘除法数字谜（一）.题库教师版 page 7 of 12

【考点】除法数字谜【难度】3 星【题型】填空【关键词】希望杯，4 年级，初赛，8 题【解析】先确定商首位是 8，再估量出除数首位是 5，确定商的末位 1，得到被除数为 4620. 【答案】 4620 【例 17】右边的除法算式中，商数是。【考点】除法数字谜【难度】3 星【题型】填空【关键词】希望杯，五年级，初赛，第 11 题，4 分【解析】除数的百位是 6，积是一个三位数，所以商的十位一定是 1,除数的个位是 7，被除数个位是 1，所以商的个位是 3，所以商是 3 【答案】 3 【例 18】右面算式中的每个“奇”字代表 1、3、5、7、9 中的一个，每个“偶”字代表 0、2、4、6、8 中的一个，为使算式成立，求出它们所代表的值。【考点】除法数字谜【难度】3 星【题型】填空【关键词】奇偶分析法【解析】为了叙述方便，把算式中每个“奇”与“偶”字都标上角码，如下式所示。奇奇偶 -奇偶偶偶因此 5偶所在位必定向“奇 2”所在位借 1，因而排除“偶 4”=0。又由于 9= 2 3 8 由于 1 偶偶偶偶偶，所以 2 =2 = 5 7 2 9 4 偶或者 3 4 6 5-1-2-2.乘除法数字谜（一）.题库教师版 page 8 of 12

资料库

5-1-2-2 乘除法数字谜（一）.教师版.doc

相关推荐

小学奥数

热门标签

最新资料