4-4-3 圆与扇形（三）.教师版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：1.38M 资料格式：doc 举报版权申诉

第1页 / 共14页

第2页 / 共14页

第3页 / 共14页

第4页 / 共14页

第5页 / 共14页

第6页 / 共14页

第7页 / 共14页

第8页 / 共14页

文本预览

圆与扇形例题精讲研究圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形，通过变动图形的位置或对图形进行分割、旋转、拼补，使它变成可以计算出面积的规则图形来计算它们的面积．圆的面积 2πr ；扇形的面积 2π r  圆的周长 2πr  ；扇形的弧长 2π  r n 360 n  360 ；．一、跟曲线有关的图形元素： ①扇形：扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形，扇形是圆的一部分．我们经常说的 1 2 圆等等其实都是扇形，而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几圆、 1 4 圆、 1 6 比如：扇形的面积  所在圆的面积分之几．那么一般的求法是什么呢？关键是 n ； 360 n 360 扇形中的弧长部分  所在圆的周长 n 360 ．扇形的周长  所在圆的周长  2 半径(易错点是把扇形的周长等同于扇形的弧长) n 360 ②弓形：弓形一般不要求周长，主要求面积．一般来说，弓形面积  扇形面积-三角形面积．(除了半圆) ③”弯角”：如图：弯角的面积  正方形-扇形 ④”谷子”：如图： “谷子”的面积  弓形面积 2 二、常用的思想方法： ①转化思想(复杂转化为简单，不熟悉的转化为熟悉的) ②等积变形(割补、平移、旋转等) ③借来还去(加减法) ④外围入手(从会求的图形或者能求的图形入手，看与要求的部分之间的”关系”) 板块、曲线型旋转问题【例 1】正三角形 ABC 的边长是 6 厘米，在一条直线上将它翻滚几次，使 A 点再次落在这条直线上，那么 A 点在翻滚过程中经过的路线总长度是多少厘米？如果三角形面积是 15 平方厘米，那么三角形在滚动过程中扫过的面积是多少平方厘米？(结果保留 π ) 4-3-3 圆与扇形题库 page 1 of 14

B A C B A 【考点】曲线型旋转问题【难度】3 星【题型】解答【解析】如图所示， A 点在翻滚过程中经过的路线为两段120 的圆弧，所以路线的总长度为： 2π 6     厘米； 2 8π 120 360 2 120  360 【答案】 24π 15 三角形在滚动过程中扫过的图形的为两个120 的扇形加上一个与其相等的正三角形，面积为： π 6  2 15 24π 15  平方厘米．    【巩固】直角三角形 ABC 放在一条直线上，斜边 AC 长 20 厘米，直角边 BC 长10 厘米．如下图所示，三角形由位置Ⅰ绕 A 点转动，到达位置Ⅱ，此时 B ，C 点分别到达 1B ， 1C 点；再绕 1B 点转动，到达位置Ⅲ，此时 A ， 1C 点分别到达 2A ， 2C 点．求 C 点经 1C 到 2C 走过的路径的长． B Ⅰ 60 C 30 A A 2 C 1 Ⅱ Ⅲ B 1 C 2 【考点】曲线型旋转问题【难度】3 星【题型】解答【解析】由于 BC 为 AC 的一半，所以  ，则弧  CAB 30  1CC 为大圆周长的 180   360  30   5 12 ，弧  2C C 为小圆 1 周长的 1 4  2π 20 1 ，而   CC C C 1 2 1 4 2π 10     5 12  【答案】 65 π 3 即为 C 点经 1C 到 2C 的路径，所以 C 点经 1C 到 2C 走过的路径的长为 50 3 (厘米)． π 5π  65 3 π  【巩固】如图，一条直线上放着一个长和宽分别为 4cm 和 3cm 的长方形Ⅰ．它的对角线长恰好是 5cm ．让这个长方形绕顶点 B 顺时针旋转 90°后到达长方形Ⅱ的位置，这样连续做三次，点 A 到达点 E 的位置．求点 A 走过的路程的长． Ⅰ Ⅱ Ⅲ Ⅳ A B C D E A 1 Ⅰ Ⅱ Ⅲ A 2 Ⅳ A B C D E 【考点】曲线型旋转问题【难度】3 星【题型】解答【解析】因为长方形旋转了三次，所以 A 点在整个运动过程中也走了三段路程(如右上图所示)．这三段路程分别是：第 1 段是弧 1AA ，它的长度是    ( cm )； 2 π 4 第 2 段是弧 1 2A A ，它的长度是第 3 段是弧 2A E ，它的长度是 2 π 5    ( cm )；    ( cm )； 2 π 3 1 4 1 4 1 4 4-3-3 圆与扇形题库 page 2 of 14

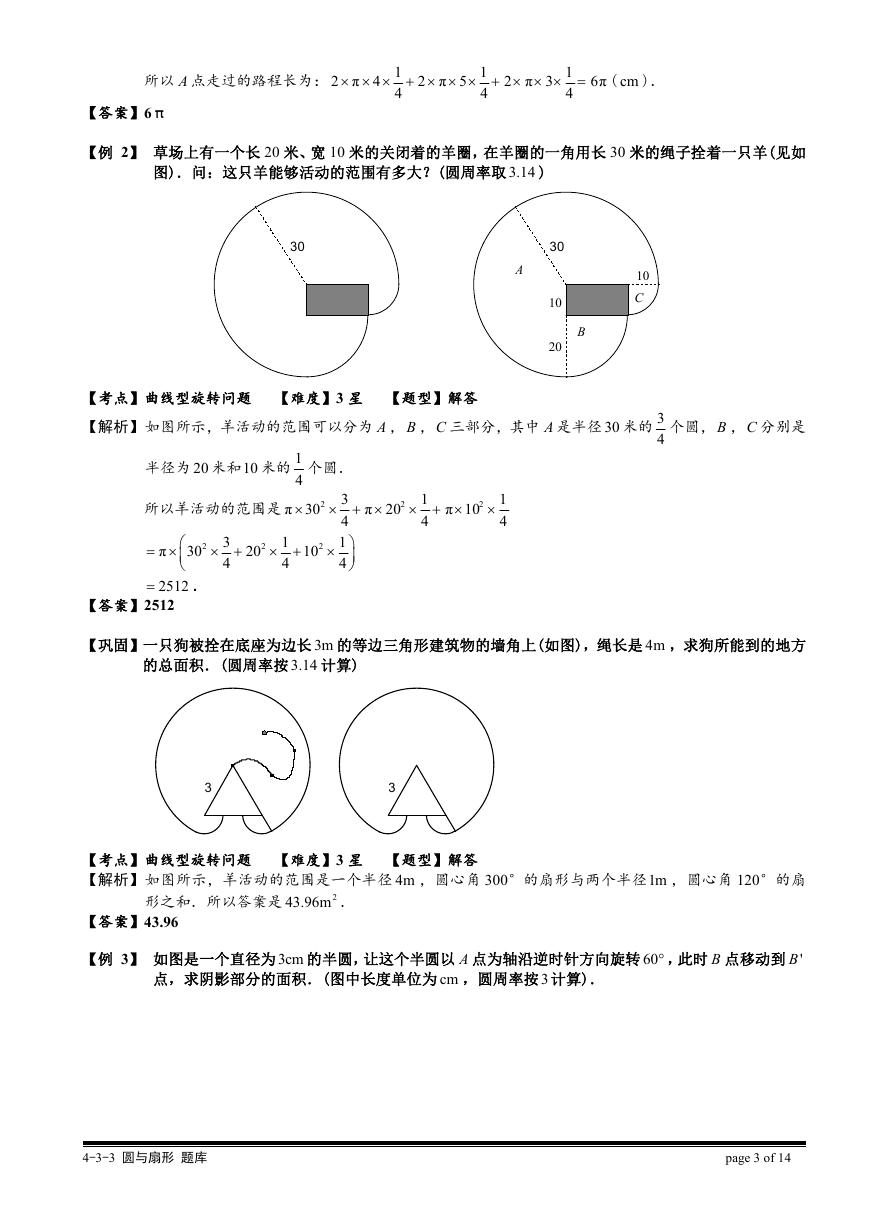
所以 A 点走过的路程长为：【答案】6π 2 π 4             2 π 5 2 π 3 6π ( cm )． 1 4 1 4 1 4 【例 2】草场上有一个长 20 米、宽 10 米的关闭着的羊圈，在羊圈的一角用长 30 米的绳子拴着一只羊(见如图)．问：这只羊能够活动的范围有多大？(圆周率取 3.14 ) 30 A 30 10 20 B 10 C 【考点】曲线型旋转问题【难度】3 星【题型】解答【解析】如图所示，羊活动的范围可以分为 A ，B ，C 三部分，其中 A 是半径 30 米的 3 4 个圆，B ，C 分别是 2    2 π 20    2 π 10 1 4  1 4 3 4 1 4    半径为 20 米和10 米的 1 4 π 30  所以羊活动的范围是个圆． 30 2   3 4 2 20   1 4 2 10    π    2512  ．【答案】2512 【巩固】一只狗被拴在底座为边长 3m 的等边三角形建筑物的墙角上(如图)，绳长是 4m ，求狗所能到的地方的总面积．(圆周率按 3.14 计算) 3 3 【考点】曲线型旋转问题【难度】3 星【题型】解答【解析】如图所示，羊活动的范围是一个半径 4m ，圆心角 300°的扇形与两个半径1m ，圆心角 120°的扇形之和．所以答案是【答案】43.96 43.96m ． 2 【例 3】如图是一个直径为 3cm 的半圆，让这个半圆以 A 点为轴沿逆时针方向旋转 60 ，此时 B 点移动到 'B 点，求阴影部分的面积．(图中长度单位为 cm ，圆周率按 3 计算)． 4-3-3 圆与扇形题库 page 3 of 14

B' 60 A B  60 360 3 2 【考点】曲线型旋转问题【难度】3 星【题型】解答【解析】面积  圆心角为 60 的扇形面积  半圆  空白部分面积(也是半圆)  圆心角为 60 的扇形面积   2 π 3  π  2 4.5(cm ) ．【答案】4.5 【例 4】如图所示，直角三角形 ABC 的斜边 AB 长为 10 厘米，  ，此时 BC 长 5 厘米．以点 B 为顺时针旋转120 ，点 A 、 C 分别到达点 E 、 D 的位置．求 AC 边扫过的图形即图 ABC 60  中心，将 ABC 中阴影部分的面积．( π 取 3) E C A B D 【考点】曲线型旋转问题【难度】3 星【题型】解答【解析】注意分割、平移、补齐． E (1) C B D (2) A  60 ABE EBD 如图所示，将图形⑴移补到图形⑵的位置，  ，那么因为则阴影部分为一圆环的 1 ． 3 1 π   3 所以阴影部分面积为 120  ， BC 2 AB   2   75  【答案】75 (平方厘米)．【巩固】如右图，以 OA 为斜边的直角三角形的面积是 24 平方厘米，斜边长 10 厘米，将它以 O 点为中心旋转 90 ，问：三角形扫过的面积是多少？( π 取 3) 4-3-3 圆与扇形题库 page 4 of 14

A O A' 【考点】曲线型旋转问题【难度】3 星【题型】解答【解析】从图中可以看出，直角三角形扫过的面积就是图中图形的总面积，等于一个三角形的面积与四分之一圆的面积之和．圆的半径就是直角三角形的斜边 OA ． π 10 10 因此可以求得，三角形扫过的面积为：    24  1 4 【答案】99  24 25π   99 (平方厘米)．【巩固】(“学而思杯”数学试题)如图，直角三角形 ABC 中， B 为直角，且 BC  厘米， 2 AC  厘米，则在将 ABC 绕 C 点顺时针旋转120 的过程中， AB 边扫过图形的面积为．( π  4 3.14 ) A A B' B C B C A' 【考点】曲线型旋转问题【难度】3 星【题型】解答 'A B C 【解析】如右上图所示，假设 ABC 旋转120 到达 '  的位置．阴影部分为 AB 边扫过的图形．从图中可以看出，阴影部分面积等于整个图形的总面积减去空白部分面积，而整个图形总面积等于的面积，由扇形 ' 于 ABC BCB 的面积之的面积之和，空白部分面积等于扇形的面积相等，所以阴影部分的面积等于扇形 BCB 的面积与 ' ACA 与扇形 'A B C  ' ' ' ACA 的面积与 ABC 的面积与 ' 'A B C 120 360 120 360 π 4     2 差，为【答案】12.56   2 π 2  4π 12.56  (平方厘米)．【例 5】如下图，△ABC是一个等腰直角三角形，直角边的长度是 1 米。现在以 C 点为圆点，顺时针旋转 90 度，那么，AB边在旋转时所扫过的面积是平方米。（=3.14）【考点】曲线型旋转问题【难度】3 星【题型】解答【解析】边扫过的面积为左下图阴影部分，可分为右下图所示的两部分。【解析】 4-3-3 圆与扇形题库 page 5 of 14

r 1 r 1 1 r 1 因为 2 r 2 r  ，所以 2 21 r  。所求面积为 2 1      1 4  2 1  1 2 【答案】0.6775 1 2      2 1  2 r     1 4  4   1 2  8  0.6775 （平方米）【例 6】如图 30-14，将长方形 ABCD 绕顶点 C 顺时针旋转 90 度，若 AB=4，BC=3，AC=5，求 AD 边扫过部分的面积．(取 3.14) 【考点】曲线型旋转问题【难度】3 星【题型】解答【解析】如下图所示，如下图所示，端点 A 扫过的轨迹为 AA A 在以 A、D 轨迹，AD， A D 所以 AD 边扫过的图形为阴影部分．显然,  ，而 AD 之间的点，扫过的轨迹  所形成的封闭图形内，且这个封闭图形的每一点都有线段 AD 上某点扫过，  ，端点 D 扫过轨迹为 DD D 有阴影部分面积为 S 直角    A D C  S 扇形  ACA  S  直角 ACD  S 扇形CD D ,而直角三角形 A D C   、ACD 面积相等．  S 扇形  S  S = S 扇形  ACA  S 扇形CD D  S = 直角  直角扇形CD D    A D C  90  360 即 AD 边扫过部分的面积为 7．065 平方厘米．  ACA 90  360 ACD  4 CD   2 4 ) AC 9 4 2 (5     2 2 7.065( ) 平方厘米【答案】7.065 【例 7】 (祖冲之杯竞赛试题)如图， ABCD 是一个长为 4 ，宽为 3 ，对角线长为 5 的正方形，它绕 C 点按顺时针方向旋转 90 ，分别求出四边扫过图形的面积． 4-3-3 圆与扇形题库 page 6 of 14

A D B C 【考点】曲线型旋转问题【难度】3 星【题型】解答【解析】容易发现， DC 边和 BC 边旋转后扫过的图形都是以线段长度为半径的圆的 1 4 ，如图： A D A' B' B C 因此 DC 边扫过图形的面积为 4π ， BC 边扫过图形的面积为 9π 4 2、研究 AB 边的情况．在整个 AB 边上，距离 C 点最近的点是 B 点，最远的点是 A 点，因此整条线段所扫过部分应该介于这两个点所扫过弧线之间，见如图中阴影部分：． A D B C A' B' 下面来求这部分的面积．观察图形可以发现，所求阴影部分的面积实际上是：扇形 'A B C 面积－三角形 ABC 面积一扇形 ' BCB 面积＝扇形 ' ACA 面积一扇形 ' ACA 面积＋三角形 ' ' 4π   BCB 面积 2 5 π 4 2 3 π 4 3、研究 AD 边扫过的图形．由于在整条线段上距离 C 点最远的点是 A ，最近的点是 D ，所以我们可以画出 AD 边扫过的图形，如图阴影部分所示： A D B C A' B' 4-3-3 圆与扇形题库 page 7 of 14

用与前面同样的方法可以求出面积为： 2 5 π 4  2 4 π 4  9 π 4 旋转图形的关键，是先从整体把握一下”变化过程”，即它是通过什么样的基本图形经过怎样的加减次序得到的．先不去考虑具体数据，一定要把思路捋清楚．最后你会发现，所有数据要么直接告诉你，要么就”藏”在那儿，一定会有．可以进一步思考，比如平行四边形的旋转问题、一般三角形的旋转问题等等，此类问题的解决对提高解决几何图形问题的能力是非常有益的．【答案】（1） BC 边扫过图形的面积为 9π 4 （2） AB 边扫过图形的面积为 4π 9π （3） AD 边扫过图形的面积为 4 （4）DC 边扫过图形的面积为 4π 【例 8】 (华杯赛初赛)半径为 25 厘米的小铁环沿着半径为 50 厘米的大铁环的内侧作无滑动的滚动，当小铁环沿大铁环滚动一周回到原位时，问小铁环自身转了几圈？【考点】曲线型旋转问题【难度】3 星【题型】解答【解析】对于这类问题，可以在初始时在小环上取一点 A ，观察半径 OA ，如图⑴，当小环沿大环内壁滚动到与初始相对的位置，即滚动半个大圆周时，如图⑵，半径 OA 也运动到了与初始时相对的位置．这时 OA 沿大环内壁才滚动了半圈．继续进行下半圈，直到 OA 与初始位置重合，这时 OA 自身转了 1 圈，因此小铁环自身也转了 1 圈． A O ⑴ O A ⑵ 【总结】对于转动的圆来说，当圆心转动的距离为一个圆周长时，这个圆也恰好转了一圈．所以本题也可以考虑小铁环的圆心轨迹，发现是一个半径与小铁环相等的圆，所以小铁环的圆心转过的距离等于自己的圆周长，那么小铁环转动了 1 圈．【答案】1 圈【巩固】如果半径为 25 厘米的小铁环沿着半径为 50 厘米的大铁环的外侧作无滑动的滚动，当小铁环沿大铁环滚动一周回到原位时，问小铁环自身转了几圈？【考点】曲线型旋转问题【难度】3 星【题型】解答【解析】如图，同样考虑小圆的一条半径 OA ，当小圆在大圆的外侧滚动一周，即滚动了大圆的半周时，半径 OA 滚动了 540 ，滚动了一圈半，所以当小圆沿大圆外侧滚动一周时，小圆自身转了 3 圈． O A ⑴ A O ⑵ 也可以考虑小圆圆心转过的距离．小圆圆心转过的是一个圆周，半径是小圆的 3 倍，所以这个圆的周长也是小圆的 3 倍，由于小圆的圆心每转动一个自身的周长时，小圆也恰好转了一圈，所以本题中小圆自身转了 3 圈．【答案】3 圈【巩固】如图所示，大圆周长是小圆周长的 n ( 1n  )倍，当小圆在大圆内侧(外侧)作无滑动的滚动一圈后又 4-3-3 圆与扇形题库 page 8 of 14

分享到：

赞收藏

资料库

4-4-3 圆与扇形（三）.教师版.doc

相关推荐

小学奥数

热门标签

最新资料