5-4-1 约数与倍数（一）.教师版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：1.11M 资料格式：doc 举报版权申诉

第1页 / 共8页

第2页 / 共8页

第3页 / 共8页

第4页 / 共8页

第5页 / 共8页

第6页 / 共8页

第7页 / 共8页

第8页 / 共8页

文本预览

5-4-1.约数与倍数（一）教学目标 1. 本讲主要对课本中的：约数、公约数、最大公约数；倍数、公倍数、最小公倍数性质的应用。 2. 本讲核心目标：让孩子对数字的本质结构有一个深入的认识，例如：（1）约数、公约数、最大公约数；倍数、公倍数、最小公倍数的内在关系；（2）整数唯一分解定理：让学生自己初步领悟“任何一个数字都可以表示为而且表达形式唯一” 知识点拨一、约数、公约数与最大公约数概念 ☆ △ △  ☆ ...   ☆ △ 的结构， (1)约数:在正整数范围内约数又叫因数,整数 a 能被整数 b 整除，a 叫做 b 的倍数，b 就叫做 a 的约数； (2)公约数:如果一个整数同时是几个整数的约数，称这个整数为它们的“公约数”； (3)最大公约数：公约数中最大的一个就是最大公约数； (4)0 被排除在约数与倍数之外 1．求最大公约数的方法 ①分解质因数法：先分解质因数，然后把相同的因数连乘起来．例如： 231 3 7 11    ， 252 2 3 7   2 2 21  ，所以 (231,252) 3 7    ； 218 12 3 9 6 3 2 ②短除法：先找出所有共有的约数，然后相乘．例如：，所以 (12,18)    ； 2 3 6 ③辗转相除法：每一次都用除数和余数相除，能够整除的那个余数，就是所求的最大公约数．用辗转相除法求两个数的最大公约数的步骤如下：先用小的一个数除大的一个数，得第一个余数；再用第一个余数除小的一个数，得第二个余数；又用第二个余数除第一个余数，得第三个余数；这样逐次用后一个余数去除前一个余数，直到余数是 0 为止．那么，最后一个除数就是所求的最大公约数．(如果最后的除数是 1，那么原来的两个数是互质的)．例如，求 600 和 1515 的最大公约数： 1515 600     ；所以 1515 和 600 的最大公约数是 15． 315 2 0    ； 600 315 1 285   ； 315 285 1 30   ；    ； 30 15 2 285 30 9 15 2．最大公约数的性质  ①几个数都除以它们的最大公约数，所得的几个商是互质数； ②几个数的公约数，都是这几个数的最大公约数的约数； ③几个数都乘以一个自然数 n ，所得的积的最大公约数等于这几个数的最大公约数乘以 n ． 3．求一组分数的最大公约数先把带分数化成假分数，其他分数不变；求出各个分数的分母的最小公倍数 a；求出各个分数的分子的最大公约数 b； b a 即为所求． 4．约数、公约数最大公约数的关系 5-4-1.约数与倍数（一）.题库教师版 page 1 of 8

（1）约数是对一个数说的；（2）公约数是最大公约数的约数，最大公约数是公约数的倍数二、倍数的概念与最小公倍数 (1)倍数:一个整数能够被另一整数整除，这个整数就是另一整数的倍数 (2)公倍数:在两个或两个以上的自然数中，如果它们有相同的倍数，那么这些倍数就叫做它们的公倍数 (3)最小公倍数：公倍数中最小的那个称为这些正整数的最小公倍数。 1. 求最小公倍数的方法 ①分解质因数的方法；例如： 231 3 7 11    ， ②短除法求最小公倍数； 252  2 2 2  3  ，所以 7 231,252   2 2 2  3 7 11 2772    ；，所以 18,12       ； 2 3 3 2 36 218 12 3 9 6 3 2 a b  ( , ) a b  ．例如： ③[ , ] a b 2. 最小公倍数的性质 ①两个数的任意公倍数都是它们最小公倍数的倍数． ②两个互质的数的最小公倍数是这两个数的乘积． ③两个数具有倍数关系，则它们的最大公约数是其中较小的数，最小公倍数是较大的数． 3. 求一组分数的最小公倍数方法步骤先将各个分数化为假分数；求出各个分数分子的最小公倍数 a ；求出各个分数分母的最大公约数 b ；b a 即为所求．例如： 3 5 , 4 12 [ ]  [3,5] (4,12)  15 4 注意：两个最简分数的最大公约数不能是整数，最小公倍数可以是整数.例如： 4．倍数、公倍数、最小公倍数的关系（1）倍数是对一个数说的；（2）最小公倍数是公倍数的约数，公倍数是最小公倍数的倍数三、最大公约数与最小公倍数的常用性质    1 4, 2 3       1,4   2,3  4 1．两个自然数分别除以它们的最大公约数，所得的商互质。如果 m 为 A 、B 的最大公约数，且 A ma ，B mb ，那么 a b、互质，所以 A 、B 的最小公倍数为 mab ，所以最大公约数与最小公倍数有如下一些基本关系：   ① A B ma mb m mab ②最大公约数是 A 、 B 、 A B 、 A B 及最小公倍数的约数．    ，即两个数的最大公约数与最小公倍数之积等于这两个数的积； 2．两个数的最大公约和最小公倍的乘积等于这两个数的乘积。即 ( , ) a b   ，此性质比较简单，学生比较容易掌握。 [ , ] a b a b  3．对于任意 3 个连续的自然数，如果三个连续数的奇偶性为 a)奇偶奇，那么这三个数的乘积等于这三个数的最小公倍数 5-4-1.约数与倍数（一）.题库教师版 page 2 of 8

210    ，210 就是 567 的最小公倍数例如： 5 6 7 b)偶奇偶，那么这三个数的乘积等于这三个数最小公倍数的 2 倍例如： 6 7 8 336    ，而 6,7,8 的最小公倍数为 336 2 168   性质（3）不是一个常见考点，但是也比较有助于学生理解最小公倍数与数字乘积之间的大小关系，即“几个数最小公倍数一定不会比他们的乘积大”。四、求约数个数与所有约数的和 1．求任一整数约数的个数一个整数的约数的个数是在对其严格分解质因数后，将每个质因数的指数(次数)加 1 后所得的乘积。如:1400 严格分解质因数之后为 3 2  ，所以它的约数有(3+1)×(2+1) ×(1+1)=4×3×2=24 个。(包括 1 和 7 5  2 1400 本身) 约数个数的计算公式是本讲的一个重点和难点，授课时应重点讲解，公式的推导过程是建立在开篇讲过的数字“唯一分解定理”形式基础之上，结合乘法原理推导出来的，不是很复杂，建议给学生推导并要求其掌握。难点在于公式的逆推，有相当一部分常考的偏难题型考察的就是对这个公式的逆用，即先告诉一个数有多少个约数，然后再结合其他几个条件将原数“还原构造”出来，或者是“构造出可能的最值”。 2．求任一整数的所有约数的和一个整数的所有约数的和是在对其严格分解质因数后，将它的每个质因数依次从 1 加至这个质因数的最高次幂求和，然后再将这些得到的和相乘，乘积便是这个合数的所有约数的和。 3 3 21000 2  3 2 2 )(1 3)(1 5 5  如： (1 2 2 此公式没有第一个公式常用，推导过程相对复杂，需要许多步提取公因式，建议帮助学生找规律性的记  ，所以 21000 所有约数的和为 7   3 5    3 5 )(1 7) 74880      2 忆即可。例题精讲模块一、求最大公约数【例 1】把一张长 1 米 3 分米 5 厘米、宽 1 米 5 厘米的纸裁成同样大小的正方形纸块，而没有剩余，问：能裁成最大的正方形纸块的边长是多少？共可裁成几块？【考点】求最大公约数【难度】2 星【题型】解答【解析】要把一张长方形的纸裁成同样大小的正方形纸块，还不能有剩余，这个正方形纸块的边长应该是长【解析】方形的长和宽的公约数．由于题目要求的是最大的正方形纸块，所以正方形纸块的边长是长方形的长和宽的最大公约数．1 米 3 分米 5 厘米＝135 厘米，1 米 5 厘米＝105 厘米， (135,105) 15 ，长方 (平方厘米)，共可形纸块的面积为135 105 14175 裁成正方形纸块14175 225 63 (平方厘米)，正方形纸块的面积为15 15 225 (张)．       【答案】边长 15，裁成 63 块【巩固】一个房间长 450 厘米，宽 330 厘米．现计划用方砖铺地，问需要用边长最大为多少厘米的方砖多少【巩固】块(整块)，才能正好把房间地面铺满？【考点】求最大公约数【难度】2 星【题型】解答【解析】要使方砖正好铺满地面，房间的长和宽都应是方砖边长的倍数，也就是方砖边长厘米数必须是房间【解析】长、宽厘米数的公约数．由于题中要求方砖边长尽可能大，所以方砖边长应为房间长与宽的最大公约数．450 和 330 的最大公约数是 30． 450 30 15  ，共需15 11 165  ， 330 30 11 (块).     【答案】边长 30，需要 165 块【例 2】将一个长和宽分别是是 1833 厘米和 423 厘米的长方形分割成若干修正在方形，则正方形最少是）个。（（A）78 （C）5 （D）6 【考点】求最大公约数【难度】2 星【题型】选择（B）7 5-4-1.约数与倍数（一）.题库教师版 page 3 of 8

【关键词】华杯赛，初赛，第 3 题【解析】本题不是求1833 与 423 的最大公约数，因为题目没有强调是相同正方形，所以应该用辗转相处法，求商，因为1833 423=4 423 141=3   【答案】 B  ，所以先切成 423 423 141  的共有 4 个剩下长方形141 423  的，所以应该还可以切成 3 个，所以一共有 4 3=7  个，选择 B 【例 3】如图，某公园有两段路，AB＝175 米，BC＝125 米，在这两段路上安装路灯，要求 A、B、C 三点各设一个路灯，相邻两个路灯间的距离都相等，则在这两段路上至少要安装路灯___个. 【考点】求最大公约数【难度】2 星【题型】填空【关键词】华杯赛，六年级，初赛，第 7 题【解析】175 与 125 的最大公约数为 25，所以取 25 米为两灯间距，175＝25×7，125＝25×5，AB 段应按 7＋1 ＝8 盏灯，BC 段应按 5＋1＝6 盏灯，但在 B 点不需重复按灯，故共需安装 8＋6－1＝13（盏）【答案】13 盏【例 4】把 20 个梨和 25 个苹果平均分给小朋友，分完后梨剩下 2 个，而苹果还缺 2 个，一共最多有多少个小朋友？【考点】求最大公约数【难度】3 星【题型】解答【解析】此题相当于梨的总数是人数的整数倍还多 2 个，苹果数是人数的整数倍还缺 2 个，所以减掉 2 个梨，【解析】补充 2 个苹果后，18 个梨和 27 个苹果就都是人数的整数倍了，即人数是 18 和 27 的公约数，要求最多的人数，即是 18 和 27 的最大公约数 9 了．【答案】9 人【例 5】有 336 个苹果，252 个桔子，210 个梨，用这些水果最多可以分成多少份同样的礼物？在每份礼物中，三样水果各多少？【考点】求最大公约数【难度】3 星【题型】解答【解析】此题本质上也是要求出这三种水果的最大公约数，有 (336,252,210) 【解析】 42 , 即可以分 42 份，每份中有苹果 8 个，桔子 6 个，梨 5 个．【答案】42 份，每份中有苹果 8 个、桔子 6 个、梨 5 个【巩固】教师节那天，某校工会买了 320 个苹果、240 个桔子、200 个鸭梨，用来慰问退休的教职工，问用这【巩固】些果品，最多可以分成多少份同样的礼物(同样的礼物指的是每份礼物中苹果、桔子、鸭梨的个数彼此相等)？在每份礼物中，苹果、桔子、鸭梨各多少个？【考点】求最大公约数【难度】3 星【题型】解答【解析】因为 (320,240,200) 【解析】 40 ，320 40 8  ， 240 40 6    ， 200 40 5  ，所以最多可分 40 份，每份中有  8 个苹果 6 个桔子，5 个鸭梨. 【答案】可分 40 份，每份中有 8 个苹果 6 个桔子，5 个鸭梨. 模块二、约数【例 6】 2004 的约数中，比 100 大且比 200 小的约数是【考点】约数【难度】1 星【题型】填空【关键词】希望杯，五年级，初赛，第 4 题，5 分【解析】2004=3×4×167，所以结果为 167 【答案】167 。【例 7】过冬了，小白兔只储存了 180 只胡萝卜，小灰兔只储存了 120 棵大白菜，为了冬天里有胡萝卜吃，小灰兔用十几棵大白菜换了小白兔的一些胡萝卜，这时他们储存的粮食数量相等，则一棵大白菜可以换__________只胡萝卜。【考点】约数【难度】2 星【题型】填空 5-4-1.约数与倍数（一）.题库教师版 page 4 of 8

【关键词】希望杯，六年级，一试，第 13 题【解析】方法一：若使他们存储粮食的数量相等，需要将小白兔的胡萝卜给小灰兔 （只），但是本题需要去换，即若干次换完后要多 30 个胡萝卜即可，若想用十几颗大白菜换，而 30 里面只有15 这个约数是十几，所以需要换 15 次，，每次换后要多 30 15=2 （只），所以 1 棵白菜换了 2 1=3 只胡萝卜 180 120 2=30      方法二：设 1 棵白菜换 x 只胡萝卜，灰兔用 a 棵白菜换胡萝卜，则   10,20 a ， 1 2 x   ，∴ 15a ax a 2 15     30 1    a x  ，，∴ 3x ，    180 ⇒ 即 1 棵白菜换了 3 只胡萝卜 a ax 120 【答案】 3 只【例 8】一个自然数，它的最大的约数和次大的约数的和是 111，这个自然数是________. 【考点】约数【难度】3 星【题型】填空【关键词】华杯赛，六年级，决赛，第 7 题【解析】因为 111 是奇数，而奇数＝奇数＋偶数，所以所求数的最大约数与次大约数必为一奇一偶。而一个数的最大约数是其自身，而一个数如有偶约数此数必为偶数，而一个偶数的次大约数应为这个偶数 1 2 的【答案】 74 ，设这个次大约数为 a，则最大约数为 2a，a＋2a＝111，求得 a＝37，2a＝74，即所求数为 74。【例 9】一个两位数有 6 个约数，且这个数最小的 3 个约数之和为 10，那么此数为几？【考点】约数【难度】3 星【题型】解答【解析】最小的三个约数中必然包括约数 1，除去 1 以外另外两个约数之和为 9，由于 9 是奇数，所以这两个【解析】约数的奇偶性一定是相反的，其中一定有一个是偶数，如果一个数包含偶约数，那么它一定是 2 的倍数，即 2 是它的约数。于是 2 是这个数第二小的约数，而第三小的约数是 7，所以这个两位数是 14 的倍数，由于这个两位数的约数中不含 3、4、5、6，所以这个数只能是 14 或 98，其中有 6 个约数的是 98．【答案】98 【例 10】如果你写出 12 的所有约数，1 和 12 除外，你会发现最大的约数是最小约数的 3 倍．现有一个整数 n，除掉它的约数 1 和 n 外，剩下的约数中，最大约数是最小约数的 15 倍，那么满足条件的整数 n 有哪些？【考点】约数【难度】3 星【题型】解答【解析】设整数 n 除掉约数 1 和 n 外，最小约数为 a，可得最大约数为15a ，那么【解析】 n 3、5、a 都为 n 的约数．因为 a 是 n 的除掉约数 1 外的最小约数，那么 3 当 3  ．所以满足条件的整数 n 有 60 和 135． 15 3  135 n  2 a  时，【答案】n 有 60 和 135 a   15 15 a a  a  ．当 2 n  a  时， 3 5 a    ．则 15 2   ； 60 2 2 2 模块三、公约数与最大公约数综合【例 11】马鹏和李虎计算甲、乙两个两位数的乘积，马鹏把甲数的个位数字看错了，得乘积 473；李虎把甲数的十位数字看错了，得乘积 407，那么甲、乙两数的乘积应是______. 【考点】公约数与最大公约数综合【难度】3 星【题型】填空【解析】乙数是 473 与 407 的公约数.473 与 407 的最大公约数是 11，11 是质数，它的两位数约数只有 11，所【解析】  ，所以甲数是 47，甲、乙两数的乘积应为：47 11 517 .  ，407 37 11    【答案】甲、乙两数的乘积应为： 47 11 517 以乙数是 11，又 473 43 11    【例 12】用 2、3、4、5、6、7 这六个数码组成两个三位数 A 和 B，那么 A、B、540 这三个数的最大公约数最大可能是___________．【考点】公约数与最大公约数综合【难度】3 星【题型】填空【解析】【解析】  2 3 3  2  ，A、B、540 这三个数的最大公约数是 540 的约数，而 540 的约数从大到小排列依 5 540 次为：540、270、180、135、108、90……由于 A 和 B 都不能被 10 整除，所以 540、270、180 都不是 A 和 B 的约数．由于 A 和 B 不能同时被 5 整除，所以 135 也不是 A 和 B 的公约数．540 的约数除 5-4-1.约数与倍数（一）.题库教师版 page 5 of 8

去这些数后最大的为 108，考虑 108 的三位数倍数，有 108、216、324、432、540、648、756、864、 972，其中由 2、3、4、5、6、7 这六个数码组成的有 324、432 和 756，易知当 A 和 B 一个为 756、另一个为 324 或 432 时，A、B、540 这三个数的最大公约数为 108，所以 A、B、540 这三个数的最大公约数最大可能是 108．【答案】108 【例 13】现有三个自然数，它们的和是 1111，这样的三个自然数的公约数中，最大的可以是多少？【考点】公约数与最大公约数综合【难度】3 星【题型】解答【解析】只知道三个自然数的和，不知道三个自然数具体是几，似乎无法求最大公约数．只能从唯一的条件“它【解析】们的和是 1111”入手分析．三个数的和是 1111，它们的公约数一定是 1111 的约数．因为1111 11 101  ，它的约数只能是 1，11，101 和 1111，由于三个自然数的和是 1111，所以三个自然数都小于 1111， 1111 不可能是三个自然数的公约数，而 101 是可能的，比如取三个数为 101，101 和 909．所以所求数是 101．  【答案】101 【例 14】10 个非零不同自然数的和是 1001，则它们的最大公约数的最大值是多少？【考点】公约数与最大公约数综合【难度】3 星【题型】解答【解析】设 M 为这 10 个非零不同自然数的最大公约数，那么这 10 个不同的自然数分别可以表示为：【解析】 1 2 2 , ( 10 ,..., , a a 2 Ma ，其中 1 Ma Ma 那么根据题意有： ( M a 1 因为 10 个不同非零自然数的和最小为 55，所以 M 最大可以为 13 ) 1001 7 11 13      ) 1  ,..., a 10 a 10 ...   a 【答案】13 【巩固】100 个非 0 自然数的和等于 2006，那么它们的最大公约数最大可能值是（【巩固】【考点】公约数与最大公约数综合【难度】3 星【题型】填空【关键词】华杯赛，决赛，第 8 题，10 分【解析】2006=2×17×59，现在要求最大公约数最大，则让整个一百个数的和除以约数后的商尽可能的小，且还应该为 2006 的一个约数，100 个非 0 自然数的和最小且符合是 2006 的一个约数的为 2×59=118。所以，最大公约数的最大可能值为 17。）。【答案】17 【例 15】三个两两不同的正整数，和为 126，则它们两两最大公约数之和的最大值为【考点】公约数与最大公约数综合【难度】5 星【题型】填空【关键词】迎春杯，高年级，决赛，11 题【解析】假设这三个数分别为 a ， b ， c ，且 a b c    ，要求的是 a b c   ，则 126 , a b ．    , b c    , a c  的最 ,a b 是 a 和 b 的最大公约数，根据辗转相除法求最大公约数的过程，可以知道  , a b a ,a b 也是 b a 和    ． b a a ， , a b     ,b c ,a b ,b c ,a c 大值．由于  ,a b a 的最大公约数，而一个数的约数不可能比这个数大，所以 ,b c ,a c 同理可得， c a   ． ,a b a ，  由 5 3 b a   ； ,b c b ， 由 4 c b  ；  ,a c a ， 由 三式相加可得  7 , a b   故   也就是说    要使等号成立，必须使五个不等式 等号都成立，即 a ，   ； ,a c b ， c b    得到   5 , 2 7 b a a b b a a       得到    3 7 , 4 c b c b b c b      得到   7 , 7 a ； c a a c      7 , 7 , 5 3 a c b a b c   4 4    , a b c a c   7 7    , a c 的最大值为 72． a ， ,b c   ， b a ,b c ,a b   ， b a ,a b b ， a ， 126 72  ． ,a b ,a b   c b   , a b , a b , b c , b c 4 7 4         a   a b c   ，  ,b c   ， c b b ， ,a c ,b c   ， c b a ，得到 2 ,a c a ， 4 a 中的 c a ， b 5-4-1.约数与倍数（一）.题库教师版 page 6 of 8

: 1: 2 : 4 a b c  时等号成立．在本题中就是 a ，b ，c 分别为 18，36，72 时它们两两最大公约数之即 : 和取得最大值 72．小结：本题的结论1: 2 : 4 较容易猜到，但证明起来较困难．另外可能会有人猜到 : 到最大值，这是错误的． 1: 2 :3 时取 a b c  : 【答案】 72 【例 16】用1 9 这九个数码可以组成 362880 个没有重复数字的九位数，求这些数的最大公约数．【考点】公约数与最大公约数综合【难度】4 星【题型】解答【解析】 1 2 【解析】，是 9 的倍数，因而 9 是这些数的公约数．又 123456789 和 123456798 这两个数只差 9，这两个数的最大公约数是它们的差的约数，即是 9 的约数，所以 9 是这两个数的最大公约数．从而 9 是这 362880 个数的最大公约数．     45 9 【答案】9 【例 17】少年宫手工组的小朋友们做工艺品“猪娃娃”。每个人先各做一个纸“猪娃娃”；接着每 2 个人合做一个泥“猪娃娃”；然后每 3 个人合做一个布“猪娃娃”；最后每 4 个人合做一个电动“猪娃娃”。这样下来，一共做了 100 个“猪娃娃”，由此可知手工组共有个小朋友。【考点】公约数与最大公约数综合【难度】3 星【题型】填空【关键词】希望杯，4 年级，1 试【解析】设有如果有 1,2,3,4  12 个人，12 个人做 12 个纸娃，6 个泥娃，4 个布娃，3 个电动娃，共 25 个，做 100 要 4 个 12 人，即 48 人. 【答案】 48 人【例 18】一根长为 L 的木棍，用红色刻度线将它分成 m 等份，用黑色刻度将它分成 n 等份（m>n）。(1)设 x 是红色与黑色刻度线重合的条数，请说明：x+1 是 m 和 n 的公约数；(2)如果按刻度线将该木棍锯成小段，一共可以得到 170 根长短不等的小棍，其中最长的小棍恰有 100 根。试确定 m 和 n 的值。【考点】公约数与最大公约数综合【难度】5 星【题型】解答【关键词】华杯赛，决赛，14 题， 10 分【解析】① 同样， ② 由题设，所以，，，，，，即 13＋n 是 13×13 的因数，13×13 只有 3 个因数：1，13， .所以，甲追上乙的位置(3 分)：③会判断丙在甲追上乙的时刻所爬行的距离(3 分)。即 13+n 是 13×13 的因数，13×13 只有 3 个因数：1，13，13。所以， 13+n= ，n= －13=156，m=12。求出正整 m，n 的另一方法：使， . 设 m＝Ka，n＝Kb，(a，b)=1，代入上式， . 5-4-1.约数与倍数（一）.题库教师版 page 7 of 8

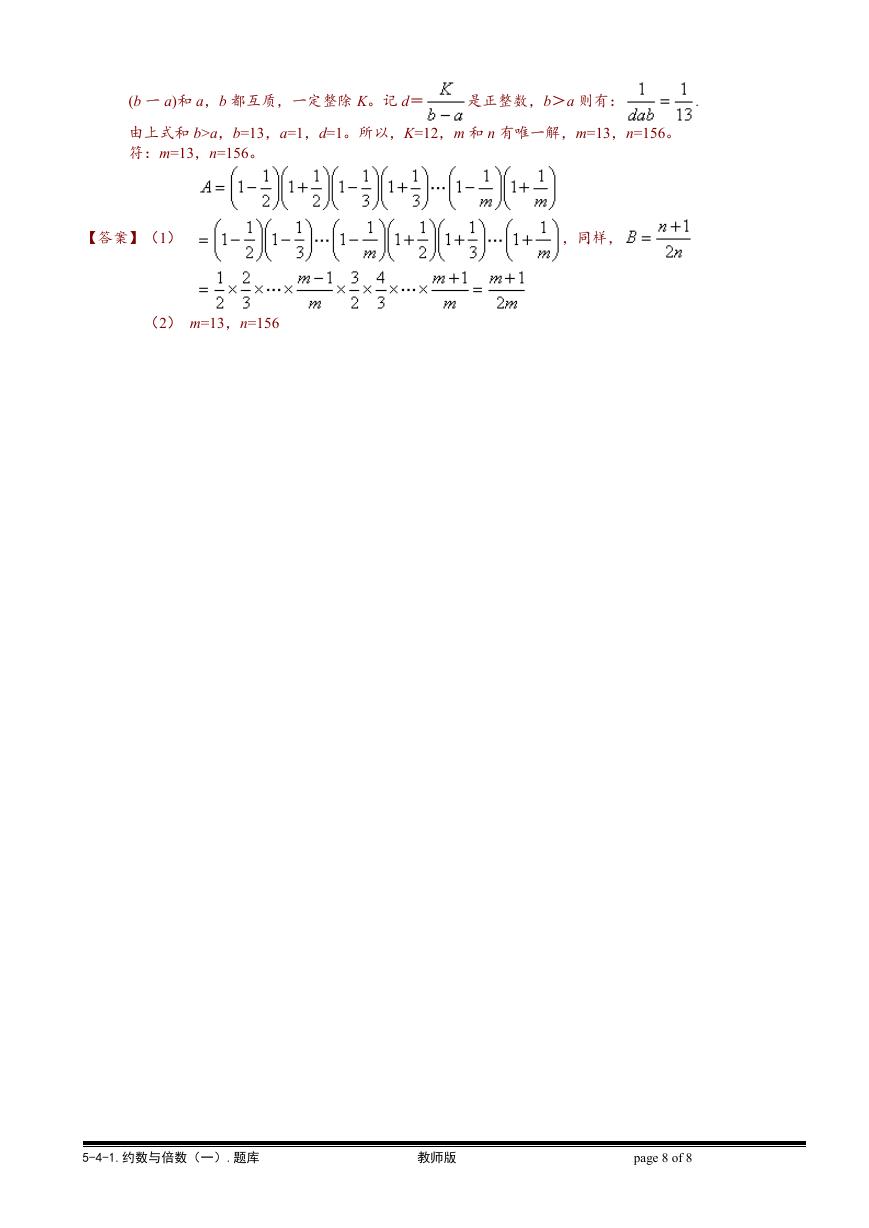
(b 一 a)和 a，b 都互质，一定整除 K。记 d＝是正整数，b＞a 则有： . 由上式和 b>a，b=13，a=1，d=1。所以，K=12，m 和 n 有唯一解，m=13，n=156。符：m=13，n=156。【答案】（1），同样，（2） m=13，n=156 5-4-1.约数与倍数（一）.题库教师版 page 8 of 8

分享到：

赞收藏

资料库

5-4-1 约数与倍数（一）.教师版.doc

相关推荐

小学奥数

热门标签

最新资料