7-7-2 容斥原理之重叠问题（二）.学生版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：0.83M 资料格式：doc 举报版权申诉

第1页 / 共6页

第2页 / 共6页

第3页 / 共6页

第4页 / 共6页

第5页 / 共6页

第6页 / 共6页

文本预览

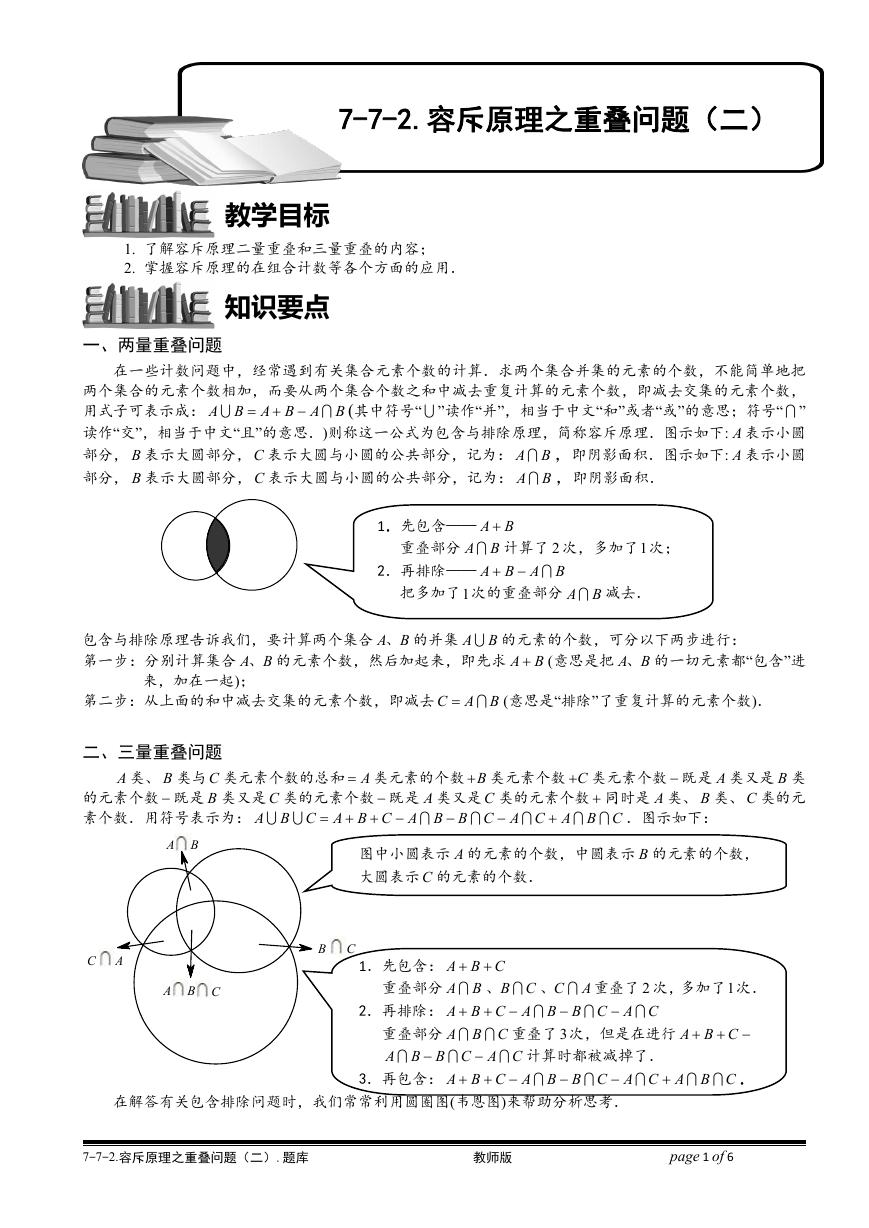
7-7-2.容斥原理之重叠问题（二）教学目标 1. 了解容斥原理二量重叠和三量重叠的内容； 2. 掌握容斥原理的在组合计数等各个方面的应用．知识要点一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，  (其中符号“  ”读作“并”，相当于中文“和”或者“或”的意思；符号“  ” 用式子可表示成： A B A B A B 读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下: A 表示小圆部分， B 表示大圆部分， C 表示大圆与小圆的公共部分，记为： A B ，即阴影面积．图示如下: A 表示小圆部分， B 表示大圆部分， C 表示大圆与小圆的公共部分，记为： A B ，即阴影面积．     1．先包含—— A B 重叠部分 A B 计算了 2 次，多加了1次； 2．再排除—— A B A B    把多加了1次的重叠部分 A B 减去．包含与排除原理告诉我们，要计算两个集合 A B、的并集 A B 的元素的个数，可分以下两步进行：第一步：分别计算集合 A B、的元素个数，然后加起来，即先求 A B (意思是把 A B、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去 C A B   (意思是“排除”了重复计算的元素个数)．二、三量重叠问题 A 类、 B 类与 C 类元素个数的总和 A 类元素的个数 B 类元素个数 C 类元素个数  既是 A 类又是 B 类的元素个数  既是 B 类又是 C 类的元素个数  既是 A 类又是 C 类的元素个数  同时是 A 类、 B 类、 C 类的元素个数．用符号表示为： A B C A B C A B B C A C A B C   ．图示如下：             A B 图中小圆表示 A 的元素的个数，中圆表示 B 的元素的个数，大圆表示 C 的元素的个数． C A B C 1．先包含： A B C   A B C 重叠部分 A B 、B C 、C A 重叠了 2 次，多加了1次．     2．再排除： A B C A B B C A C     重叠了 3 次，但是在进行 A B C 重叠部分 A B C A B B C A C  计算时都被减掉了．               在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考． 3．再包含： A B C A B B C A C A B C   ．     7-7-2.容斥原理之重叠问题（二）.题库教师版 page 1 of 6

例题精讲模块一、三量重叠问题【例 1】一栋居民楼里的住户每户都订了 2 份不同的报纸。如果该居民楼的住户只订了甲、乙、丙三种报纸，其中甲报 30 份，乙报 34 份，丙报 40 份，那么既订乙报又订丙报的有___________户。【考点】三量重叠问题【难度】3 星【题型】填空【关键词】希望杯，4 年级，1 试【解析】总共有（30＋34＋40）  2＝52 户居民，订丙和乙的有 52－30＝22 户。【答案】 22 户【例 2】某班学生手中分别拿红、黄、蓝三种颜色的小旗，已知手中有红旗的共有 34 人，手中有黄旗的共有 26 人，手中有蓝旗的共有18 人．其中手中有红、黄、蓝三种小旗的有 6 人．而手中只有红、黄两种小旗的有 9 人，手中只有黄、蓝两种小旗的有 4 人，手中只有红、蓝两种小旗的有 3 人，那么这个班共有多少人？【考点】三量重叠问题【难度】3 星【题型】解答 A B C 【解析】如图，用 A 圆表示手中有红旗的， B 圆表示手中有黄旗的， C 圆表示手中有蓝旗的．如果用手中有红旗的、有黄旗的与有蓝旗的相加，发现手中只有红、黄两种小旗的各重复计算了一次，应减去，手中有三种颜色小旗的重复计算了二次，也应减去，那么，全班人数为： 34 26 18  ） 6 2 50   【答案】 50 人 9 4 3 (人)．   ）（（    【巩固】某班有 42 人，其中 26 人爱打篮球，17 人爱打排球，19 人爱踢足球，9 人既爱打篮球又爱踢足球，4 人既爱打排球又爱踢足球，没有一个人三种球都爱好，也没有一个人三种球都不爱好．问：既爱打篮球又爱打排球的有几人？【考点】三量重叠问题【难度】3 星【题型】解答【解析】由于全班 42 人没有一个人三种球都不爱好，所以全班至少爱好一种球的有 42 人．根据包含排除法，既爱打篮球又爱打排球的人数 0），得到既爱打篮球又爱打排球的人数 9 4    （ 26 17 19 42  ）（  (人)．为： 49 42 7    【答案】 7 人【例 3】四年级一班有 46 名学生参加 3 项课外活动．其中有 24 人参加了数学小组，20 人参加了语文小组，参加文艺小组的人数是既参加数学小组也参加文艺小组人数的 3．5 倍，又是 3 项活动都参加人数的 7 倍，既参加文艺小组也参加语文小组的人数相当于 3 项都参加的人数的 2 倍，既参加数学小组又参加语文小组的有 10 人．求参加文艺小组的人数．【考点】三量重叠问题【难度】3 星【题型】解答【解析】设参加数学小组的学生组成集合 A，参加语文小组的学生组成集合 B，参加文艺小组的学生组成集   ，   =46，A =24，B =20，C =3.5，A C =7 A B C 合 G．三者都参加的学生有 z 人．有 A B C B C =2 A B C 因为 A B C A  所以 46=24+20+7x-10-2x-2x+x，解得 x=3，即三者的都参加的有 3 人．那么参加文艺小组的有 3 7=21 人．   ， A B =10．  B C   B C A B A C         A B C   ，【答案】 21 人 7-7-2.容斥原理之重叠问题（二）.题库教师版 page 2 of 6

【巩固】五年级三班学生参加课外兴趣小组，每人至少参加一项．其中有 25 人参加自然兴趣小组，35 人参加美术兴趣小组，27 人参加语文兴趣小组，参加语文同时又参加美术兴趣小组的有 12 人，参加自然同时又参加美术兴趣小组的有 8 人，参加自然同时又参加语文兴趣小组的有 9 人，语文、美术、自然 3 科兴趣小组都参加的有 4 人．求这个班的学生人数．【考点】三量重叠问题【难度】3 星【题型】解答【解析】设参加自然兴趣小组的人组成集合 A，参加美术兴趣小组的人组成集合日，参加语文兴趣小组的人组成集合 C． A =25， B =35， C =27， B C =12， A B A B C  所以，这个班中至少参加一项活动的人有 25+35+27-12-8-9+4=62，而这个班每人至少参加一项．即这个班有 62 人． =8， A C =9， A B C B C    = A A B C   .   =4. B C A B A C        【答案】 62 人【巩固】光明小学组织棋类比赛，分成围棋、中国象棋和国际象棋三个组进行，参加围棋比赛的有 42 人，参加中国象棋比赛的有 55 人，参加国际象棋比赛的有 33 人，同时参加了围棋和中国象棋比赛的有18 人，同时参加了围棋和国际象棋比赛的有10 人，同时参加了中国象棋和国际象棋比赛的有 9 人，其中三种棋赛都参加的有 5 人，问参加棋类比赛的共有多少人？  【考点】三量重叠问题【难度】3 星【题型】解答【解析】根据包含排除法，先把参加围棋比赛的 42 人，参加中国象棋比赛的 55 人与参加国际象棋比赛的 33 人加起来，共是 42 55 33 130  人．把重复加一遍同时参加围棋和中国象棋的18 人，同时参加围棋和国际象棋的10 人与同时参加中国象棋和国际象棋的 9 人减去，但是，同时参加了三种棋赛的 5 人被加了 3 次，又被减了 3 次，其实并未计算在内，应当补上，实际上参加棋类比赛的共有： 130 或者根据学过的公式：A B C A B C A B B C A C A B C 人数为： 42 55 33 18 10 9 5 98   ，参加棋类比赛的总 (人)．     (人)． 18 10 9    5 98      （）              【答案】 98 人【例 4】新年联欢会上，共有 90 人参加了跳舞、合唱、演奏三种节目的演出．如果只参加跳舞的人数三倍于只参加合唱的人数；同时参加三种节目的人比只参加合唱的人少 7 人；只参加演奏的比同时参加演奏、跳舞但没有参加合唱的人多 4 人；50 人没有参加演奏；10 人同时参加了跳舞和合唱但没有参加演奏；40 人参加了合唱；那么，同时参加了演奏、合唱但没有参加跳舞的有________人．【考点】三量重叠问题【难度】3 星【题型】填空【关键词】西城实验【解析】设只参加合唱的有 x 人，那么只参加跳舞的人数为 3x ，由 50 人没有参加演奏、10 人同时参加了跳【解析】舞和合唱但没有参加演奏，得到只参加合唱的和只参加跳舞的人数和为 50 10  人，即 x  ，所以只参加合唱的有10 人，那么只参加跳舞的人数为 30 人，又由“同时参加 x 三种节目的人比只参加合唱的人少 7 人”，得到同时参加三项的有 3 人，所以参加了合唱的人中“同时参加了演奏、合唱但没有参加跳舞的”有： 40 10 10 3 17  ，得 10   人． 3 x 40 40    【答案】17 人【巩固】六年级 100 名同学，每人至少爱好体育、文艺和科学三项中的一项．其中，爱好体育的 55 人，爱好文艺的 56 人，爱好科学的 51 人，三项都爱好的 15 人，只爱好体育和科学的 4 人，只爱好体育和文艺的 17 人．问：有多少人只爱好科学和文艺两项？只爱好体育的有多少人？【考点】三量重叠问题【难度】3 星【题型】解答【解析】只是 A 类和 B 类的元素个数，有别于容斥原理Ⅱ中的既是 A 类又是 B 类的元数个数．依题意，画图如下．设只爱好科学和文艺两项的有 x 人．由容斥原理，列方程得 55 56 51 15 100 17 15 4 15  ）（）（  （ 15  ）        x 7-7-2.容斥原理之重叠问题（二）.题库教师版 page 3 of 6

即  100 55 56 51 17 4   111 x  11 x     x 15 2 100   只爱好体育的有： 55 17 15 4 19     (人)．【答案】11人只爱好科学和文艺，19 人只爱好体育。【例 5】在某个风和日丽的日子，10 个同学相约去野餐，每个人都带了吃的，其中 6 个人带了汉堡，6 个人带了鸡腿， 4 个人带了芝士蛋糕，有 3 个人既带了汉堡又带了鸡腿，1 个人既带了鸡腿又带了芝士蛋糕． 2 个人既带了汉堡又带了芝土蛋糕．问： ⑴ 三种都带了的有几人？ ⑵ 只带了一种的有几个？【考点】三量重叠问题【难度】4 星【题型】解答 B A C 【解析】如图，用 A 圆表示带汉堡的人， B 圆表示带鸡腿的人， C 圆表示带芝士蛋糕的人． ⑴ 根据包含排除法，总人数 （带汉堡的人数  带鸡腿的人数  带芝士蛋糕的人数 ）（带汉堡、鸡腿的人数  带汉堡、芝士蛋糕的人数  带鸡腿、芝士蛋糕的人数 ）三种都带了的人数，即 10 ）三种都带了的人数，得三种都带了的人数为：10 10 0 3 2 1     (人)． 6 6 4   ）（  （  ⑵ 求只带一种的人数，只需从 10 人中减去带了两种的人数，即10  （ 3 2 1   ） (人)．只带了一种  4  的有 4 人．【答案】（1）0 人，（2） 4 人【巩固】盛夏的一天，有10 个同学去冷饮店，向服务员交了一份需要冷饮的统计表：要可乐、雪碧、橙汁的各有 5 人；可乐、雪碧都要的有 3 人；可乐、橙汁都要的有 2 人；雪碧、橙汁都要的有 2 人；三样都要的只有1 人，证明其中一定有1 人这三种饮料都没有要．【考点】三量重叠问题【难度】4 星【题型】解答【解析】略【答案】根据根据包含排除法，至少要了一种饮料的人数  (要可乐的人数  要雪碧的人数  要橙汁的人数)  (要可乐、雪碧的人数  要可乐、橙汁的人数  要雪碧、橙汁的人数)  三种都要的人数，即至   (人)，所以其中有1 人这三种少要了一种饮料的人数为： 5 5 5 饮料都没有要． (人)．10 9 1 3 2 2   1 9     ）（（）  【例 6】全班有 25 个学生，其中17 人会骑自行车，13 人会游泳，8 人会滑冰，这三个运动项目没有人全会，至少会这三项运动之一的学生数学成绩都及格了，但又都不是优秀．若全班有 6 个人数学不及格，那么，⑴ 数学成绩优秀的有几个学生？ ⑵ 有几个人既会游泳，又会滑冰？【考点】三量重叠问题【难度】4 星【题型】解答【解析】⑴ 有 6 个数学不及格，那么及格的有：25 6 19   （ (人)，即最多不会超过19 人会这三项运动之一．而 (人)至少会这三项运动之一．于又因为没人全会这三项运动，那么，最少也会有： 17 13 8  是，至少会三项运动之一的只能是19 人，而这19 人又不是优秀，说明全班 25 人中除了19 人外，剩下的 6 名不及格，所以没有数学成绩优秀的． ⑵ 上面分析可知，及格的19 人中，每人都会两项运动：会骑车的一定有一部分会游泳，一部分会滑冰；会游泳的人中若不会骑车就一定会滑冰，而会滑冰的人中若不会骑车就一定会游泳，但既会游泳又会滑冰的人一定不会骑自行车．所以，全班有19 17  (人)既会游泳又会滑冰． 2 19   ） 2   【答案】（1）0 人，（2） 2 人【巩固】五年级一班共有 36 人，每人参加一个兴趣小组，共有 A 、 B 、 C 、 D 、 E 五个小组，若参加 A 组的有15 人，参加 B 组的人数仅次于 A 组，参加 C 组、 D 组的人数相同，参加 E 组的人数最少，只有 4 人．那么，参加 B 组的有_______人．【考点】三量重叠问题【难度】4 星【题型】填空【解析】参加 B ，C ， D 三组的总人数是 36 15 4 17    (人)，C ， D 每组至少 5 人，当 C ， D 每组 6 人时， 7-7-2.容斥原理之重叠问题（二）.题库教师版 page 4 of 6

B 组为 5 人，不符合题意，所以参加 B 组的有17 5 5 7    (人)．【答案】 7 人【例 7】五一班有 28 位同学，每人至少参加数学、语文、自然课外小组中的一个．其中仅参加数学与语文小组的人数等于仅参加数学小组的人数，没有同学仅参加语文或仅参加自然小组，恰有 6 个同学参加数学与自然小组但不参加语文小组，仅参加语文与自然小组的人数是 3 个小组全参加的人数的 5 倍，并且知道 3 个小组全参加的人数是一个不为 0 的偶数，那么仅参加数学和语文小组的人有多少人？【考点】三量重叠问题【难度】4 星【题型】解答【解析】参加 3 个小组的人数是一个不为 0 的偶数，如果该数大于或等于 4，那么仅参加语文与自然小组的人数则大于等于 20，而仅参加数学与自然小组的人有 6 个，这样至少应有 30 人，与题意矛盾，所以参加 3 个小组的人数为 2．仅参加语文与自然小组的人数为 10，于是仅参加语文与自然、仅参加数学与自然和参加 3 个小组的人数一共是 18 人，剩下的 10 人是仅参加数学与语文以及仅参加数学的．由于这两个人数相等，所以仅参加数学和语文小组的有 5 人．【答案】 5 人【例 8】在一个自助果园里，只摘山莓者两倍于只摘李子者；摘了草莓、山莓和李子的人数比只摘李子的人数多 3 个；只摘草莓者比摘了山莓和草莓但没有摘李子者多 4 人； 50 个人没有摘草莓；11个人摘了山莓和李子但没有摘草莓；总共有 60 人摘了李子.如果参与采摘水果的总人数是100 ，你能回答下列问题吗？ ① 有 ② 有 ③ 有 ④ 有 ⑤ 有人摘了山莓；人同时摘了三种水果；人只摘了山莓；人摘了李子和草莓，而没有摘山莓；人只摘了草莓. 【考点】三量重叠问题【难度】3 星【题型】填空【解析】如图，根据题意有【解析】    50 60   2A C 3 G C  4 B E  A D C  11D  C D F G   40 A B E   A  ， 9B  ， 13 代入求解： 26      所以①有 ②有16 人同时摘了三种水果； ③有 26 人只摘了山莓； ④有 20 人摘了李子和草莓，而没有摘山莓； ⑤有 9 人只摘了草莓. 26 11 5 16 58 A D E G   C  ， 11D  ， 5E  ， 20 F  ， 16 G   (人)摘了山莓；【答案】①有 58 (人)摘了山莓；②有16 人同时摘了三种水果； ③有 26 人只摘了山莓；④有 20 人摘了李子和草莓，而没有摘山莓； ⑤有 9 人只摘了草莓. 【例 9】某学校派出若干名学生参加体育竞技比赛，比赛一共只有三个项目，已知参加长跑、跳高、标枪三个项目的人数分别为 10、15、20 人，长跑、跳高、标枪每一项的的参加选手中人中都有五分之一的人还参加了别的比赛项目，求这所学校一共派出多少人参加比赛？ 7-7-2.容斥原理之重叠问题（二）.题库教师版 page 5 of 6

体育 55 人 4 17 15 56 人文艺 x 科学 51 人【考点】三量重叠问题【难度】4 星【题型】解答【解析】由条件可知，参加长跑的人中有 2 人参加其它项目，参加跳高的人中有 3 人参加其它项目，参加标枪的人中有 4 人还参加别的项目，假设只参加长跑和跳高的人数为 x，只参加长跑和标枪的人数为 y，只参加标枪和跳高的有 z 人，三项都参加的有 n 人.那么有以下方程组：由条件可知，参加长跑的人中有 2 人参加其它项目，参加跳高的人中有 3 人参加其它项目，参加标枪的人中有 4 人还参加别的项目，假设只参加长跑和跳高的人数为 x，只参加长跑和标枪的人数为 y，只参加标枪和跳高的有 z 人，三项都参加的有 n 人.那么有以下方程组： x y n         x n z      z y n  2 3 4 将 3 条等式相加则有 2（x+y+z）+3n=9，由这个等式可以得到，n 必须是奇数，所以，n 只能是 1 或 3、5、7……，如果 n≥3 时 x、y、z 中会出现负数.所以 n=1，这样可以求得 x=0，y=1，z=2.由此可得到这个学校一共派出了 10+15+20-0-1-2-2×1=40 人. 将 3 条等式相加则有 2（x+y+z）+3n=9，由这个等式可以得到，n 必须是奇数，所以，n 只能是 1 或 3、5、7……，如果 n≥3 时 x、y、z 中会出现负数.所以 n=1，这样可以求得 x=0，y=1，z=2.由此可得到这个学校一共派出了 10+15+20-0-1-2-2×1=40 人. 【答案】 40 人模块二、四个量的重叠问题【例 10】养牛场有 2007 头黄牛和水牛，其中母牛 1105 头，黄牛 1506 头，公水牛 200 头，那么母黄牛有头。【考点】四个量的重叠问题【难度】3 星【题型】填空【关键词】希望杯，4 年级，1 试【解析】解：公牛有 2007-1105=902 头，公黄牛有 902-200=702 头，母黄牛有 1506-702=804 头【答案】 804 头【例 11】一个书架上有数学、语文、英语、历史 4 种书共 35 本，且每种书的数量互不相同。其中数学书和英语书共有 l6 本，语文书和英语书共有 17 本：有一种书恰好有 9 本，这种书是书。【考点】四个量的重叠问题【难度】4 星【题型】填空【关键词】迎春杯，四年级，初赛，5 题【解析】如果数学书有 x 本，那么英语书有 16-x 本，语文书有 17- （ 16-x ） =x+1 本，历史书为【解析】 35-(x+16-x+x+1)=18-x 本，其中有可能出现相等的有 x 和 16-x，x 和 18-x 因为它们奇偶性相同.为了不相等，x≠8 且 x≠9，有此得到 16-x 不等于 8 和 7，x+1 不等于 9 和 10，18-x 不等于 10 和 9，只有 16-x 可以等于 9，所以英语书有 9 本. 【答案】英语 7-7-2.容斥原理之重叠问题（二）.题库教师版 page 6 of 6

分享到：

赞收藏

资料库

7-7-2 容斥原理之重叠问题（二）.学生版.doc

相关推荐

小学奥数

热门标签

最新资料