7-8-3 几何计数（三）.学生版.doc

发布时间：2023-11-21 发布人：admin 分类：养殖资料大小：0.84M 资料格式：doc 举报版权申诉

第1页 / 共10页

第2页 / 共10页

第3页 / 共10页

第4页 / 共10页

第5页 / 共10页

第6页 / 共10页

第7页 / 共10页

第8页 / 共10页

文本预览

7-8-3.几何计数（三）教学目标 1.掌握计数常用方法； 2.熟记一些计数公式及其推导方法； 3.根据不同题目灵活运用计数方法进行计数．本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等，并渗透分类计数和用容斥原理的计数思想．知识要点一、几何计数在几何图形中，有许多有趣的计数问题，如计算线段的条数，满足某种条件的三角形的个数，若干个图分平面所成的区域数等等．这类问题看起来似乎没有什么规律可循，但是通过认真分析，还是可以找到一些处理方法的．常用的方法有枚举法、加法原理和乘法原理法以及递推法等．n 条直线最多将平面分成个部分；n 个圆最多分平面的部分数为 n(n-1)+2；n 个三角形将平面最多分成 2 2 3        n …… 2) n 2 ( n 1 2 3n(n-1)+2 部分；n 个四边形将平面最多分成 4n(n-1)+2 部分…… 在其它计数问题中，也经常用到枚举法、加法原理和乘法原理法以及递推法等．解题时需要仔细审题、综合所学知识点逐步求解．排列问题不仅与参加排列的事物有关，而且与各事物所在的先后顺序有关；组合问题与各事物所在的先后顺序无关，只与这两个组合中的元素有关．二、几何计数分类数线段：如果一条线段上有 n+1 个点(包括两个端点)（或含有 n 个“基本线段”），那么这 n+1 个点把这条线段一共分成的线段总数为 n+(n-1)+…+2+1 条数角：数角与数线段相似，线段图形中的点类似于角图形中的边．数三角形：可用数线段的方法数如右图所示的三角形（对应法），因为 DE 上有 15 条线段，每条线段的两端点与点 A 相连，可构成一个三角形，共有 15 个三角形，同样一边在 BC 上的三角形也有 15 个，所以图中共有 30 个三角形．数长方形、平行四边形和正方形：一般的，对于任意长方形（平行四边形），若其横边上共有 n 条线段，纵边上共有 m 条线段，则图中共有长方形（平行四边形）mn 个．例题精讲模块一、立体几何计数【例 1】用同样大小的正方体小木块堆成如下图的立体图形，那么一共用了__________块小正方体。 7-8-3.几何计数（三）.题库教师版 page 1 of 10

【考点】立体图形几何计数【难度】3 星【题型】填空【关键词】迎春杯，中年级，初试，6 题，走美杯，4 年级，决赛，第 8 题【解析】一共有：【解析】【答案】 50 块  1 4 9     （块）。 50 34  【例 2】将 32 个相同的小正方体拼成一个体积为 32 立方厘米的长方体，将表面涂上红漆，然后分开，其中有 2 个面涂红的小正方体有 24 个，则有1 个面涂红的小正方体有个。【考点】立体图形几何计数【难度】3 星【题型】填空【关键词】学而思杯，4 年级，第 7 题【解析】 2 ，所以这个长方体的尺寸只有1 1 32 5 32 其中只有尺寸为 2 2 8 小正方体有 0 个。【答案】 0   五种情况，   的长方体的表面染色后，有 24 个正方体有 2 个面涂红，所以有1个面涂红的   ，1 2 16   ，1 4 8   ， 2 4 4   ， 2 2 8 【例 3】如图是一个由 27 个棱长为 1 的白色小正方体木块粘成的棱长为 3 的正方体木块，现任意挖去其中的 3 个棱长为 1 的小正方体，然后将所有暴露在外的表面全部刷上蓝漆，那么余下的 24 个棱长为 1 的小正方体中恰好有 3 面涂蓝漆的最多能有____个. 【考点】立体图形几何计数【难度】3 星【题型】填空【关键词】学而思杯，5 年级，第 12 题【解析】1）角块本身为 3 面暴露在外的小方块； 2）挖去外侧面中部的小方块，能够增加 4 块三面暴露在外的小方块，加上角块，共形成 8 块 3 面涂漆的小方块，为最优方案 3）因此挖去对称的 2 块外侧中部的小方块后，将产生 16 块 3 面暴露在外的小方块 4）然后再挖去任意一个外侧面中部的小方块，将增加 3 块 3 面暴露在外的小方块，但同时破坏原来的 2 块 3 面在外的小方块. 5）所以最多有 17 块 3 面涂漆的小方块【答案】17 模块二、几何计数的应用【例 4】如图，每个小正方形的面积都是 l 平方厘米。则在此图中最多可以画出__________个面积是 2 平方厘米的格点正方形(顶点都在图中交叉点上的正方形)。【考点】几何计数的应用【难度】3 星【题型】填空【关键词】希望杯，4 年级，1 试【解析】每两行正方形可确定 3 个面积是 2 平方厘米的格点正方形,总共有:3×3=9(个) 【答案】 9 【巩固】图中的每个小方格都是面积为 1 的正方形，面积为 2 的矩形有个。【考点】几何计数的应用【难度】3 星【题型】填空【关键词】希望杯，五年级，二试，第 8 题【解析】4×4+3×5=31 【答案】 31个 7-8-3.几何计数（三）.题库教师版 page 2 of 10

【巩固】下图是由 25 个面积等于 1 的小正方形组成的大正方形，图中面积是 6 的长方形有个。【考点】几何计数的应用【难度】3 星【题型】填空【关键词】希望杯，四年级，二试，第 4 题【解析】每两行正方形可确定 3 个面积是 2 平方厘米的格点正方形,总共有: 3 4 2 【答案】 24 个    24 (个) 【例 5】如图所示，在边长为 1 的小正方形组成的 4×4 方格图中，共有 25 个格点。在以格点为顶点的直角三角形中，两条直角边长分别是 1 和 3 的直角三角形共有个。【考点】几何计数的应用【难度】3 星【题型】填空【关键词】华杯赛，决赛，第 2 题【解析】我们把一排连续三个正方形叫做三连正方形，三连正方形的个数乘上每个三连正方形中直角三角形的个数就得到所求的总数：4×2×2×4＝64 （个）【答案】 64 【例 6】用 9 个钉子钉成相互间隔为 1 厘米的正方阵(如右图)．如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形，这样得到的三角形中，面积等于 1 平方厘米的三角形的个数有多少？面积等于 2 平方厘米的三角形有多少个？【解析】面积等于 1 平方厘米的三角形有 32 个．面积等于 2 平方厘米的三角形有 8 个． (1)面积等于 1 平方厘米的分类统计如下：底为 2，高为 1 3×2=6(个) 底为 2，高为 1 3×2=6(个) 底为 1，高为 2 3×2=6(个) 底为 1，高为 2 3×2=6(个) 2×2=4(个) 所以，面积等于 1 平方厘米的三角形的个数有：6+6+6+6+4+4=32(个)． (2)面积等于 2 平方厘米的分类统计如下： 2×2=4(个) 底为 2，高为 1 底为 1，高为 2 3×2=6(个) 1×2=2(个) 所以，面积等于 2 平方厘米的三角形的个数有：6+2=8(个)． 7-8-3.几何计数（三）.题库教师版 page 3 of 10

【例 7】下图中的正方形被分成 9 个相同的小正方形，它们一共有 16 个顶点（共同的顶点算一个），以其中不在一条直线上的 3 个点为顶点，可以构成三角形．在这些三角形中，与阴影三角形有同样大小面积的有多少个？【考点】几何计数的应用【难度】3 星【题型】解答【解析】1．显然应先求出阴影三角形的面积【解析】设原正方形的边长是 3，则小正方形的边长是 1，阴影三角形的面积是 ½×2×3=3 2．思考图中怎样的三角形的面积等于 3 （1）一边长 2，这边上的高是 3 的三角形的面积等于 3（即形如图中阴影三角形）．这时，长为 2 的边只能在原正方形的边上，这样的三角形有 2×4×4=32（个）；（2）一边长 3，这边上的高是 2 的三角形的面积等于 3．这时，长为 3 的边是原正方形的一边或平行于一边的分割线．这样的三角形有 8×2=16（个）注意：不能与（1）中的三角形重复，所以这样的三角形共有 32+16=48（个）．【答案】 48 个【巩固】图中每个小正方形的边长都是 l 厘米，则在图中最多可以画出面积是 3 平方厘米的格点三角形(顶点在图中交叉点上的三角形)____个。【考点】几何计数的应用【难度】3 星【题型】填空【关键词】希望杯，五年级，一试，第 11 题【解析】由三角形面积为 3 平方厘米,可知三角形的底×高为 6，6=1×6=2×3，因为图形中长方形的长为 3 厘米，宽为 2 厘米。当三角形的底=3 厘米时，有 4×2=8 种情况，；当底=2 厘米时，有 1×2=2 种情况。所以，一共有 8+2=10 个。【答案】10 个【例 8】在一个圆周上有 8 个点，正好把圆周八等分，以这些点为顶点作三角形，可以作出个等腰三角形．【考点】几何计数的应用【难度】4 星【题型】解答【解析】由于 8 个点正好把圆周八等分，所以以其中的任何 3 个点作为顶点都不能组成等边三角形．那么任【解析】意选取其中的一个点作为顶点，一个顶点上有三个不同的等腰三角形，圆周上有 8 个顶点，所以一   个等腰三角形，而且这些等腰三角形互不相同(否则，假设其中有两个等腰三角形相同，共有 3 8 24 这两个等腰三角形不可能是同一个顶点，只能是不同的顶点，这样这个等腰三角形必定是正三角形，与前面的分析不合)，所以可以作出 24 个等腰三角形．【答案】 24 个等腰三角形【例 9】圆周上十个点，任意两点之间连接一条弦，这些弦在圆内有多少个交点？【考点】几何计数的应用【难度】4 星【题型】解答【解析】圆周上 4 点构成一个四边形，四边形两条对角线相交可以产生一个交点．问题转化为“圆周上 10 个【解析】点可以组成多少个以他们为定点的四边形？”利用上一讲的知识，去掉重复的部分，可知有： 10 9 8 7     个．所以交点有 210 个． 4 3 2 1       210 【答案】 210 个【例 10】圆周上有8 个点，两点所连的线段叫“弦”，每两点连一条弦，各弦无公共端点，共可连四条弦，各弦互不相交的连法共有________种．【考点】几何计数与找规律【解析】本题可以利用归纳的方法解决．若圆周上只有 2 个点，只有1种连法；【解析】【难度】4 星【题型】解答 7-8-3.几何计数（三）.题库教师版 page 4 of 10

  种连法； 2 若圆周上只有 4 个点，先选中 1 个点，它可以与相邻的两个点相连，它连好后其它两点只有 1 种连法，所以此时有1 2 若圆周上只有 6 个点，先选中 1 个点，此时它可以与相邻的 2 个点相连，也可以相对的 1 个点相连，若与相邻的点相连，剩下的 4 个点有 2 种连法；若与相对的点相连，剩下的 4 个点只有 1 种连法，所以此时有 2 2 1 5 若圆周上只有 8 个点，先选中一个点，此时它可以与相邻的 2 个点相连，也可以与与它相隔 2 个点的另外两个点相连．若与相邻的点相连，剩下的 6 个点有 5 种连法；若与相隔两个点的点相连，剩下的 6 个点被分成两边，一边 2 个点，只有一种连法，一边 4 个点，有 2 种连法．所以此时共有 5 2 2 2 14     种连法．    种连法；【答案】14 种连接法【例 11】九个大小相等的小正方形拼成了右图．现从点 A 走到点 B，每次只能沿着小正方形的对角线从一个顶点到另一个顶点，不允许走重复路线（如图的虚线就是一种走法）．那么从点 A 走到点 B 共有 ________种不同的走法．【考点】几何计数的应用【难度】4 星【题型】填空【关键词】迎春杯，五年级，初试，10 题【解析】路线相当于右图中从 A 到 B 的不同路线（不走重复路线），从 A 到 C、D 到 B 方法都唯一，从 C 出【解析】发有 3 种方向，从 D 出发也有 3 种方向（不一定是最短路线），根据乘法原理，共有 339 种不同走法。【答案】 9 种【例 12】国际象棋中“马”的走法如图所示，位于○位置的“马”只能走到标有×的格中．在 5×5 个方格的国际象棋棋盘上（如右图）放入四枚白马（用○表示）和四枚黑马（用●表示）．要求将四枚白马移至四枚黑马的位置，将四枚黑马移至四枚白马的位置，而且必须按照国际象棋的规则，棋子只能移动到空格中，每个格最多放一枚棋子．那么最少需要__________步．【考点】几何计数的应用【难度】5 星【题型】填空【关键词】迎春杯，四年级，初赛，4 题【解析】需要移动 8 枚棋子，任意棋子只移动一步是无法到达目的空格当中的，所以，最少需要 8 2 16 【解析】   步，具体方案：如下图，用四步交换两枚棋子到目的空格当中．用同样的方法处理其他 6 枚棋子．一共需要16 步． 3 2 1 4 【答案】16 步【例 13】请将三个“数”、三个“学”、三个“美”填入右图中，使得每一横排、每一竖排都有这三个字，如果在左上角摆上“数”，那么可能有_______几种不同的摆法。 7-8-3.几何计数（三）.题库教师版 page 5 of 10

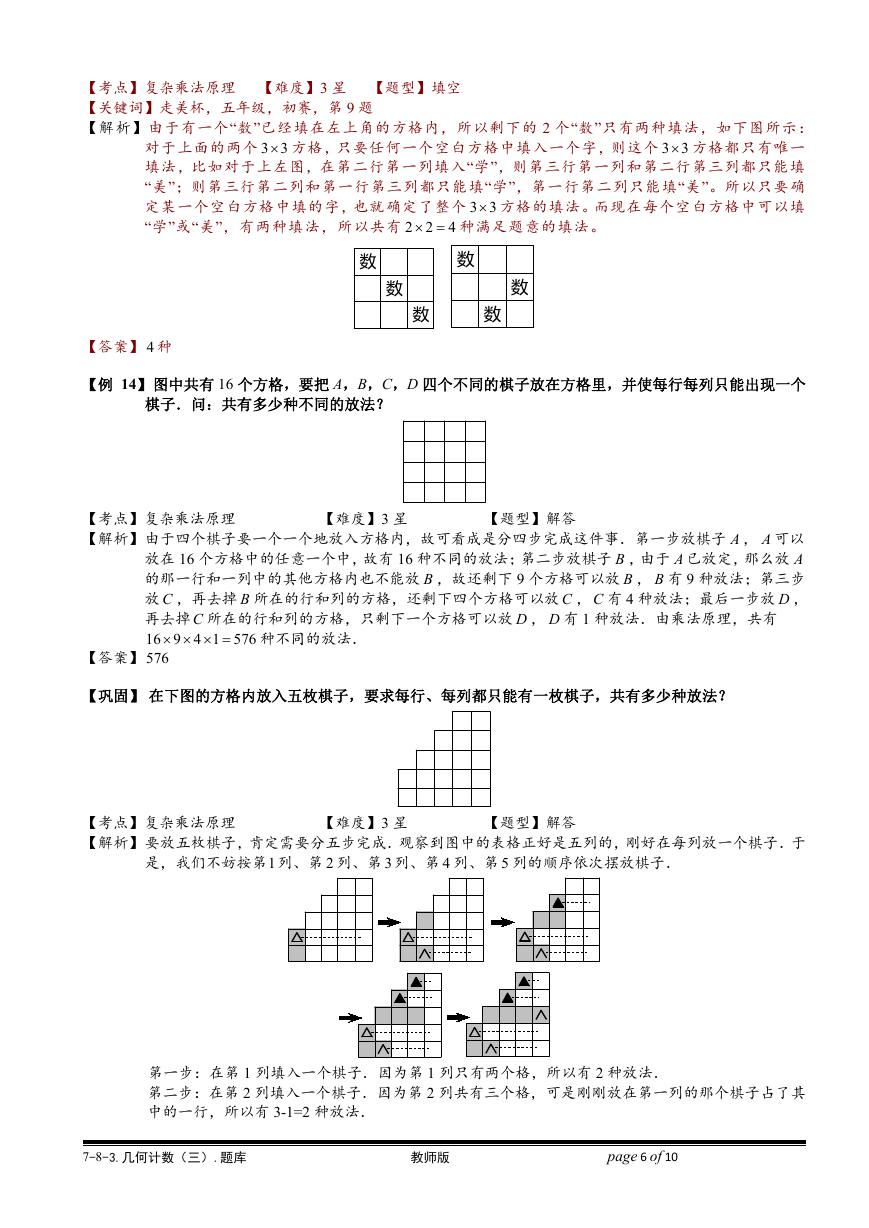
【考点】复杂乘法原理【难度】3 星【题型】填空【关键词】走美杯，五年级，初赛，第 9 题【解析】由于有一个“数”已经填在左上角的方格内，所以剩下的 2 个“数”只有两种填法，如下图所示：对于上面的两个 3 3 方格，只要任何一个空白方格中填入一个字，则这个 3 3 方格都只有唯一填法，比如对于上左图，在第二行第一列填入“学”，则第三行第一列和第二行第三列都只能填 “美”；则第三行第二列和第一行第三列都只能填“学”，第一行第二列只能填“美”。所以只要确定某一个空白方格中填的字，也就确定了整个 3 3 方格的填法。而现在每个空白方格中可以填 “学”或“美”，有两种填法，所以共有 2 2   种满足题意的填法。 4 数数数数数数【答案】 4 种【例 14】图中共有 16 个方格，要把 A，B，C，D 四个不同的棋子放在方格里，并使每行每列只能出现一个棋子．问：共有多少种不同的放法？【难度】3 星【考点】复杂乘法原理【解析】由于四个棋子要一个一个地放入方格内，故可看成是分四步完成这件事．第一步放棋子 A ， A 可以放在 16 个方格中的任意一个中，故有 16 种不同的放法；第二步放棋子 B ，由于 A 已放定，那么放 A 的那一行和一列中的其他方格内也不能放 B ，故还剩下 9 个方格可以放 B ， B 有 9 种放法；第三步放 C ，再去掉 B 所在的行和列的方格，还剩下四个方格可以放 C ， C 有 4 种放法；最后一步放 D ，再去掉 C 所在的行和列的方格，只剩下一个方格可以放 D ， D 有 1 种放法．由乘法原理，共有 16 9 4 1 576     种不同的放法．【题型】解答【答案】 576 【巩固】在下图的方格内放入五枚棋子，要求每行、每列都只能有一枚棋子，共有多少种放法？【考点】复杂乘法原理【解析】要放五枚棋子，肯定需要分五步完成．观察到图中的表格正好是五列的，刚好在每列放一个棋子．于【题型】解答【难度】3 星是，我们不妨按第1列、第 2 列、第 3 列、第 4 列、第 5 列的顺序依次摆放棋子．第一步：在第 1 列填入一个棋子．因为第 1 列只有两个格，所以有 2 种放法．第二步：在第 2 列填入一个棋子．因为第 2 列共有三个格，可是刚刚放在第一列的那个棋子占了其中的一行，所以有 3-1=2 种放法． 7-8-3.几何计数（三）.题库教师版 page 6 of 10

第三步：在第 3 列填入一个棋子．因为第 3 列共有四个格，可是被放在第一列、第二列的那两个棋子各占了一行，所以有 4-2=2 种放法．第四步：在第 4 列填入一个棋子．同理推得有 5-3=2 种放法．第五步：在第 5 列填入一个棋子．同理推得有 5-4=1 种放法．根据乘法原理，往方格内放入 5 枚棋子，每行每列只有一枚棋子，共有 2 2 2 2 1 16      种放法．【答案】16 【例 15】下图是一个中国象棋盘，如果双方准备各放一个棋子，要求它们不在同一行，也不在同一列，那么总共有多少种不同的放置方法？楚河汉界【考点】复杂乘法原理【解析】第一个棋子有 90 种放法，第二个棋子有 72 种放法，根据乘法原理，共有 90 72 6480 【题型】解答   【难度】3 星（种）不同的放置方法．【答案】 6480 【巩固】国际象棋棋盘是 8×8 的方格网，下棋的双方各有 16 个棋子位于 16 个区格中，国际象棋中的“车” 同中国象棋中的“车”一样都可以将位于同一条横行或竖行的对方棋子吃掉，如果棋局进行到某一时刻，下棋的双方都只剩下一个“车”，那么这两个“车”位置有多少种情况？【考点】复杂乘法原理【解析】对于如果只有一只“车”的情况，它可以有 64 种摆放位置，如果在棋盘中再加入一个“车”，那么它不能在原来那个“车”的同行或同列出现，他只能出现在其他七行七列，所以它只有 7×7=49 中摆放，所以这两个“车”的摆放位置有 64×49=3136 种方法．【题型】解答【难度】3 星【答案】3136 模块三、几何计数与找规律【例 16】下图的两个图形（实线）是分别用 10 根和 16 根单位长的小棍围成的．如果按此规律（每一层比上面一层多摆出两个小正方形）围成的图形共用了 60 多根小棍，那么围成的图形有几层，共用了多少根小棍？【考点】几何计数与找规律【难度】2 星【题型】解答【解析】通过观察每增加一层，恰好增加 6 根小棍，这 6 根恰好是增加那一层比上一层多摆出的两个正方形多用的，即前 1 层用 4 根，前 2 层用 4+6 根，前 3 层用 4+6×2 根，前 n 层用 4+6×(n-1)根，现在共用了 60 多根，应减去 4 是 6 的倍数，所以共用小棍 64 根，围成的图形有 11 层．【答案】11层， 64 根【例 17】如图所示，用长短相同的火柴棍摆成 3×1996 的方格网，其中每个小方格的边都由一根火柴棍组成，那么一共需用多少根火柴棍? 【考点】几何计数与找规律【难度】2 星【题型】解答 7-8-3.几何计数（三）.题库教师版 page 7 of 10

【解析】横放需 1996×4 根，竖放需 1997×3 根,共需 1996×4+1997×3=13975 根．【解析】【答案】13975 根【例 18】用 3 根等长的火柴可以摆成一个等边三角形．如图用这样的等边三角形拼合成一个更大的等边三角形.如果这个大等边三角形的每边由 20 根火柴组成，那么一共要用多少根火柴? 【考点】几何计数与找规律【难度】2 星【题型】解答【解析】把大的等边三角形分为“20”层分别计算火柴的根数：【解析】最上一层只用了 3 根火柴；从上向下数第二层用了 3×2=6 根；从上向下数第二层用了 3×3=9 根； ……从上向下数第二层用了 3×20=60 根；所以总共要用火柴 3×（1+2+3+……+20）=630．【答案】 630 【巩固】用三根火柴可拼成一个小“△”，若用 108 根火柴拼成如图所示形状的大三角形，请你数一数共有多少个三角形？【考点】几何计数与找规律【解析】首先，需弄清形状如图的大三角形共有多少层．从上往下，第一层用 3 3 1 【解析】【难度】2 星【题型】解答         n 36  3 n  108              根火柴；第四层用12 3 4   根火柴．根据题意，有： 3 6 9 12 15   根火柴；第五层用15 3 5    根火柴；第二层用 6 3 2     根火柴；…；第 n ，故，所以， 8n  ，即形状如图的大三角形共有 8 层，是边长为 8 根火柴的根火柴；第三层用 9 3 3 层用 3 3n n 1 2 3 4 5      大正三角形．然后，数出共有多少个三角形．尖朝上的三角形共： (1 2 3 4 5 6 7 8) (1 2 3 4 5)   尖朝下的三角形共： (1 2 3 4 5 6 7) 所以，共有三角形：120 50 170 本题小结：尖朝上的三角形：每一种尖朝上的三角形个数都是由 1 开始的连续自然数的和，其中连续自然数最多的和中最大的加数就是三角形每边被分成的基本线段的条数，依次各个连续自然数的和都比上一次少一个最大的加数，直到 1 为止．尖朝下的三角形的个数也是从 1 开始的连续自然数的和，它的第一个和恰是尖朝上的第二个和，依次各个和都比上一个和少最大的两个加数，以此类推直到零为止． (1 2 3)       (个)．        (1 2 3 4 5 6 7)   (1 2) 1 120      (1 2 3 4 5)       (1 2 3 4 5 6)    (1 2 3) 1 0 50        (1 2 3 4)    (个)； (个)；   【答案】170 个【例 19】 3 根火柴可以摆成一个小三角形。图中用很多根火柴摆成了一个中空的大三角形。已知大三角形外沿上每条边都是 20 根火柴。摆成这个图共需要根火柴。 7-8-3.几何计数（三）.题库教师版 page 8 of 10

分享到：

赞收藏

资料库

7-8-3 几何计数（三）.学生版.doc

相关推荐

小学奥数

热门标签

最新资料