Freescale Semiconductor
Application Note
Document Number: AN4246
Rev. 0, 06/2011
Calibrating an eCompass in the
Presence of Hard and Soft Iron
Interference
Contents
11
2
3
4
5
6
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1 Key Words . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.2 Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
The Hard and Soft Iron Model . . . . . . . . . . . . . . . . . . . . . 2
Applying Hard and Soft Iron Corrections to the
Tilt-Compensated eCompass . . . . . . . . . . . . . . . . . . . . . 3
Relating the Locus of Magnetometer Measurements to
Calibration Coefficients . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Imposing a Symmetric Constraint onto the Inverse Soft Iron
Matrix. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Calibration Algorithms and Source Code . . . . . . . . . . . . 9
by: Talat Ozyagcilar
Applications Engineer
Introduction
1
This application note provides the theory for the in-situ
calibration of a smartphone electronic compass
(eCompass) for hard and soft iron effects. The
mathematical framework is that which is developed in
AN4248 “Implementing a Tilt-Compensated eCompass
using Accelerometer and Magnetometer Sensors” and
AN4247 “Layout Recommendations for PCBs Using a
Magnetometer Sensor.” It is therefore highly
recommended to read these application notes first before
reading this document.
Key Words
1.1
eCompass, Geomagnetic, Magnetometer, Hard Iron, Soft
Iron, Calibration.
© Freescale Semiconductor, Inc., 2011. All rights reserved.
�
The Hard and Soft Iron Model
1.2
•
Summary
It is possible for a smartphone eCompass to be calibrated by the owner in the street with no a priori
knowledge of location or the direction of magnetic north.
• Measurements of the geomagnetic field made during the calibration process lie on the surface of
an ellipsoid defined by the three coefficients of a hard iron vector and the six coefficients of the
inverse soft iron matrix.
• The nine optimum calibration coefficients are computed so as to transform the magnetic field from
the surface of the measurement ellipsoid to the surface of a sphere centred at the origin.
It is a straightforward process to correct for known hard and soft iron effects in the tilt-compensated
eCompass algorithms and software.
•
• Reference C source code for the calibration can be licensed free of charge from Freescale for use
in any product using a Freescale magnetometer. Please contact your Freescale sales representative
for the license agreement.
The Hard and Soft Iron Model
2
AN4248 equation 4 defines the magnetic field Bp measured by a smartphone magnetometer in the absence
of hard and soft iron effects after rotations in yaw ψ, pitch θ and roll φ by the rotation matrices Rz(ψ), Ry(θ),
and Rx(φ) as:
Bp
R= x
φ(
)Ry θ(
)Rz ψ(
)Br Rx φ(
=
)Ry θ(
)Rz ψ(
)B
δcos
⎞
⎛
⎟
⎜
0
⎜
⎟
δsin⎝
⎠
Eqn. 1
Br is the local geomagnetic field vector with magnitude B and magnetic inclination δ at the smartphone
location.
The application note AN4247, section 6, defines the hard iron offset as resulting from permanently
magnetized ferromagnetic components on the PCB. Since the magnetometer and PCB rotate together, the
hard iron offset is a simple vector VPCB, which adds to the magnetometer reading. AN4247, section 6, also
notes that any zero field offset in the magnetometer factory calibration will appear as a fixed additive
vector VSensor. For convenience, both offsets are normally combined as a single 'hard iron' vector V defined
as:
Including these terms in Equation 1 gives:
V
=
VPCB VSensor
+
Bp
R= x
φ(
)Ry θ(
)Rz ψ(
)B
δcos
⎞
⎛
⎟
⎜
0
⎜
⎟
δsin⎝
⎠
V+
Eqn. 2
Eqn. 3
AN4247 defines the soft iron effect as the interfering magnetic field induced by the geomagnetic field onto
normally unmagnetized ferromagnetic components on the PCB. The assumption is made that the induced
soft iron field is linearly related to the geomagnetic field measured in the rotated smartphone reference
Calibrating an eCompass in the Presence of Hard and Soft Iron Interference, Rev. 0
2
Freescale Semiconductor
�
Applying Hard and Soft Iron Corrections to the
frame by the 3 x 3 matrix WSoft. The linearity assumption is generally accurate but is not strictly true in
the presence of magnetic hysteresis effects present in either the magnetometer or in ferromagnetic
components on the PCB.
The magnetometer is normally calibrated by the supplier to have approximately equal gain in all three
axes. Any remaining differences in gains can be modeled by a diagonal gain matrix WGain.
A final matrix, WNonOrthog, can be used to model: i) the rotation of the magnetometer sensor relative to the
smartphone coordinate system and ii) the lack of perfect orthogonality between sensor axes.
For convenience, all three matrices are combined into a single 3 x 3 soft iron matrix W defined as:
Including the soft iron matrix W into Equation 3 now defines the magnetometer reading after arbitrary
smartphone rotations as:
W WNonOrthogWGainWSoft
=
Eqn. 4
Bp WR=
x
φ( )Ry θ(
)Rz ψ(
)B
δcos
⎞
⎛
⎟
⎜
0
⎟
⎜
δsin⎝
⎠
V+
Eqn. 5
3
Applying Hard and Soft Iron Corrections to the
Tilt-Compensated eCompass
The application note AN4248 provides the mathematics and reference C source code for a
tilt-compensated eCompass with correction for hard-iron interference only. This section extends the
mathematics in AN4248 to include the soft iron interference defined by the matrix W in Equation 5.
Equations 13 and 15 in AN4248 define the roll φ and pitch θ angles as a function of the accelerometer
sensor only. These equations are independent of magnetic interference and are therefore valid in the
presence of hard and soft iron effects.
The effects of the soft iron matrix W can be included in equation 16 in AN4248 by manipulating
Equation 5 to give:
Rz ψ(
)B
δcos
⎞
⎛
⎟
⎜
0
⎟
⎜
δsin⎝
⎠
=
⎛
⎜
⎜
⎜
⎝
ψcos
ψsin–
0
ψsin
0
ψcos
0
1
0
B
δcos
⎞
⎛
⎜
⎟
0
⎟
⎜
δsin⎝
⎠
⎞
⎟
⎟
⎟
⎠
=
Ry θ–(
)Rx φ–(
)W 1– Bp V–
(
)
Eqn. 6
Equation 16 in AN4248 and Equation 6 are identical except for the presence of the inverse soft iron matrix
W-1 operating on the vector (Bp - V).
Calibrating an eCompass in the Presence of Hard and Soft Iron Interference, Rev. 0
Freescale Semiconductor
3
�
Applying Hard and Soft Iron Corrections to the Tilt-Compensated eCompass
Expanding the components of Equation 6 gives Equations 7 and 8 below, These equations differ from
equations 20 and 21 in AN4248 in that the vector
is now the magnetometer reading corrected to
the flat plane φ =θ = 0 with both hard and soft iron effects removed.
⎛
⎜
⎜
⎜
⎝
Bfx
Bfy
Bfz
⎞
⎟
⎟
⎟
⎠
cos
ψB δcos
=
Bfx
ψsin B δcos
=
B– fy
⎛
⎜
⎜
⎜
⎝
Bfx
Bfy
Bfz
⎞
⎟
⎟
⎟
⎠
=
Ry θ–(
)Rx φ–(
)W 1– Bp V–
(
Eqn. 7
Eqn. 8
Eqn. 9
)
The yaw or compass heading angle ψ is determined from the ratio of Equations 7 and 8 to give Equation 10
which is analogous to equation 22 in AN4248:
ψ Bfy–
⎞
----------
tan
⎠
Bfx
=
⎛
⎝
Eqn. 10
The extension to the C source code listed in AN4248 to incorporate both soft and hard iron corrections is
equally trivial. In AN4248, section 6.1, the hard iron vector V alone is subtracted from magnetometer
reading to give Bp - V:
/* subtract the hard iron offset */
iBpx -= iVx;
iBpy -= iVy;
iBpz -= iVz;
Both hard and soft iron interference are removed by computing W-1(Bp - V) from the magnetometer
reading Bp. The inverse soft iron matrix is assumed stored in Q15 fractional integer format with entries in
the range -32768 to +32767 representing the range -1. to 0.9999.
/* 32 bit scratch integers */
int iSumx, iSumy, iSumz;
/* subtract the hard iron offset */
iBpx -= iVx;
iBpy -= iVy;
iBpz -= iVz;
/* multiply by the inverse soft iron offset */
iSumx = (InvW[0, 0] * iBpx) + (InvW[0, 1] * iBpy) + (InvW[0, 2] * iBpz);
iSumy = (InvW[1, 0] * iBpx) + (InvW[1, 1] * iBpy) + (InvW[1, 2] * iBpz);
iSumz = (InvW[2, 0] * iBpx) + (InvW[2, 1] * iBpy) + (InvW[2, 2] * iBpz);
/* return the resulting vector invW*(Bp-V) back into 16 bit Bp */
iBpx = (short)(iSumx >> 15);
iBpy = (short)(iSumy >> 15);
iBpz = (short)(iSumz >> 15);
Calibrating an eCompass in the Presence of Hard and Soft Iron Interference, Rev. 0
4
Freescale Semiconductor
�
Relating the Locus of Magnetometer Measurements to
Incorporating both hard and soft iron corrections into the tilt-compensated eCompass algorithm is
therefore trivial if these calibration coefficients are known. Note that the geomagnetic field strength B and
inclination angle δ cancel in going from Equations 7 and 8 to Equation 10. The only calibration values
used in the code sample above are the components of the hard iron vector V and the inverse soft iron matrix
W-1.
The next sections discusses how V and W-1 can be computed from measurements made by the smartphone
in the complete absence of any a priori information about the direction and strength of the geomagnetic
field vector.
4
Relating the Locus of Magnetometer Measurements to
Calibration Coefficients
Application note AN4247 introduces the concept of the locus of magnetometer measurements from an
experimental perspective. This allows the PCB designer to visually determine the level of hard and soft
iron interference prior to final PCB fabrication.
The same locus of magnetometer measurements represents the primary information available to the
calibration algorithms to determine the hard and soft iron calibration V and W-1. Under arbitrary rotation
of the smartphone by its owner, the magnetometer readings lie on a surface which can be derived from
Equation 5 to be:
{
W 1– Bp V–
(
)
}TW 1– Bp V–
(
)
=
Rx φ(
)Ry
θ(
)Rz
ψ(
)B
⎧
⎪
⎨
⎪
⎩
δcos
⎞
⎛
⎜
⎟
0
⎜
⎟
δsin⎝
⎠
T
⎫
⎪
⎬
⎪
⎭
Rx φ(
)Ry
θ(
)Rz
ψ(
)B
δcos
⎞
⎛
⎜
⎟
0
⎜
⎟
δsin⎝
⎠
⇒
(
Bp V–
)T W 1–
{
}TW 1– Bp V–
(
)
B2=
Eqn. 11
Eqn. 12
The general expression defining the locus of the vector R lying on the surface of an ellipsoid with center
at R0 is (where A must be a symmetric matrix):
Equations 12 and 13 are similar since it can be proved that the matrix A = {W-1}T W-1 is symmetric:
R R0–(
)TA R R0–(
)
=
const
Eqn. 13
AT
=
{
{
W 1–
}TW 1–
}T
=
Eqn. 14
In general therefore, the locus of magnetometer measurements forms the surface of the ellipsoid defined
by Equation 12. In the absence of hard iron effects (V = 0) and of soft iron effects (W-1 = I where I is the
identity matrix), Equation 12 simplifies to the equation of a sphere with radius B centred at the origin:
{
W 1–
}T W 1–
{
{
}T
}T
{
W 1–
}TW 1–
=
=
A
Bp
TBp
=
B2
Calibrating an eCompass in the Presence of Hard and Soft Iron Interference, Rev. 0
Freescale Semiconductor
Eqn. 15
5
�
Imposing a Symmetric Constraint onto the Inverse Soft Iron Matrix
In the presence of hard iron effects only V ≠ 0, W-1 = I, Equation 12 simplifies to the equation of a sphere
centered at the hard iron vector V:
(
Bp V–
)T Bp V–
(
)
=
B2
Eqn. 16
Hard iron effects therefore displace the locus of magnetometer measurements away from the origin and
soft iron effects distort the measurement locus from the surface of a sphere to the surface of an ellipsoid.
Equation 12 is defined by nine coefficients directly related to the required calibration coefficients: i) the
three elements of the hard iron vector V and ii) the six elements of the symmetric matrix {W-1}TW-1. The
geomagnetic field strength B is a simple scaling factor which can be determined independently.
The calibration process can therefore be summarized as i) obtaining a set of measurements Bp of the
geomagnetic field vector at different smartphone orientations and ii) fitting the nine calibration
coefficients to the measurement locus. The next section describes one additional constraint to be applied
to the inverse soft iron matrix W-1.
5
Imposing a Symmetric Constraint onto the Inverse
Soft Iron Matrix
Equation 4 defines the linear soft iron model as derived from the product of three independent
3 x 3 matrices resulting in nine independent elements in the matrix. Using the magnetometer measurement
locus in Equation 12 results in the soft iron matrix appearing as the symmetric product matrix
A = {W-1}TW-1 with only six independent coefficients. The mathematical process by which three degrees
of freedom are lost is simple to follow in Equations 11and 12. Physically, it can be understood as a result
of the loss of angle information in the construction of the ellipsoidal measurement locus since this is a
function of the magnetometer measurements only. The yaw or compass angle ψ, is unavailable since it is
not known until the magnetic calibration is complete. Roll φ and pitch angle θ information can be
associated with the magnetic readings in the magnetometer locus but exploiting them through Equation 5
requires knowing or solving for the geomagnetic field inclination angle δ.
The simplest solution is to impose the constraint that the inverse soft iron matrix W-1 also be symmetric
with six degrees of freedom. The argument for this constraint is discussed next.
Equation 5 relates each magnetometer measurement to the smartphone orientation, to the true hard iron
offset V and the true soft iron matrix W. If the readings Bp are corrected by an estimated hard iron offset
VCal and an estimated soft iron matrix VCal, then the resulting corrected magnetometer reading B'p is given
by:
B′p W 1–
Cal
=
(
Bp VCal
–
) W 1–
Cal
=
⎧
⎪
⎨
⎪
⎩
WRx φ(
)Ry θ(
)Rz ψ(
)B
⎛
⎜
⎜
⎜
⎝
⎞
δcos
⎟
⎟
0
⎟
δsin
⎠
+
–(
V VCal
)
⎫
⎪
⎬
⎪
⎭
Eqn. 17
Calibrating an eCompass in the Presence of Hard and Soft Iron Interference, Rev. 0
6
Freescale Semiconductor
�
Imposing a Symmetric Constraint onto the Inverse Soft Iron
If the calibration algorithm correctly estimates the hard and soft iron coefficients,
then the corrected locus of readings lies on the surface of a sphere centered at the origin:
W 1–
Cal
W I=
(
B′p
)TB′p
=
⎧
⎪
⎨
⎪
⎩
Rx φ(
)Ry θ(
)Rz ψ(
)B
⎛
⎜
⎜
⎜
⎝
⎞
δcos
⎟
⎟
0
⎟
δsin
⎠
T
⎫
⎪
⎬
⎪
⎭
Rx φ(
)Ry θ(
)Rz ψ(
)B
⎛
⎜
⎜
⎜
⎝
⎞
δcos
⎟
⎟
0
⎟
δsin
⎠
B2=
, VCal = V,
Eqn. 18
The converse is not the case. An arbitrary rotation can be included in the estimated inverse soft iron matrix
W 1–
and this would still result in the corrected locus of measurements lying on the surface of a sphere
Cal
centred at the origin. This is because a sphere is still a sphere under arbitrary rotation. Mathematically, if
W 1–
, where R(ω) is an arbitrary rotation matrix by angle ω, then (using the result that the
Cal
transpose of any rotation matrix R(ω)T is identical to rotation by the inverse angle R(-ω)):
W R ω(
)
=
(
B′p
)TB′p
=
⎧
⎪
⎨
⎪
⎩
R ω(
)Rx φ( )Ry θ(
)Rz ψ(
)B
⎛
⎜
⎜
⎜
⎝
⎞
δcos
⎟
⎟
0
⎟
δsin
⎠
T
⎫
⎪
⎬
⎪
⎭
R ω(
)Rx φ(
)Ry θ(
)Rz ψ(
)B
⎛
⎜
⎜
⎜
⎝
⎞
δcos
⎟
⎟
0
⎟
δsin
⎠
B2=
Eqn. 19
If the constraint is applied that W-1 is symmetric, then it is impossible for any spurious rotation angle and
error in compass heading to be introduced by the calibration process.
A further understanding of the advantage of a symmetric inverse soft iron matrix can be obtained by
relating the eigenvectors of the matrix A to the eigenvectors of the inverse soft iron matrix W-1. The
eigenvectors Xi and eigenvalues ei of the inverse soft iron matrix W-1 are defined by:
Eqn. 20
Given that W-1 is symmetric then: i) the eigenvectors of the matrix A are identical to the eigenvectors Xi
of W-1 and ii) the eigenvalues of A are the square of the eigenvalues ei of W-1:
W 1– Xi
=
eiXi
AXi
=
{
W 1–
}TW 1– Xi
=
{
W 1–
}TeiXi
=
eiW 1– Xi
=
ei
2 Xi
Eqn. 21
Since the eigenvectors of the matrix A represent the principal axes of the magnetometer measurement
ellipsoid (the Principal Axis Theorem in geometry), then constraining the inverse soft iron matrix W-1 to
be symmetric shrinks the ellipsoid into a sphere along the principal axes of the ellipsoid without applying
any additional spurious rotation.
Comparing equations 12 and 13 and using the symmetry property of W-1, the hard and soft iron magnetic
calibration parameters are related to the magnetometer ellipsoid locus by:
V
=
R0
Calibrating an eCompass in the Presence of Hard and Soft Iron Interference, Rev. 0
Freescale Semiconductor
Eqn. 22
7
�
Calibration Algorithms and Source Code
{
W 1–
}TW 1–
=
W 1– W 1–
1
---
2
A=
W 1–⇒
=
A
Eqn. 23
AN4247 illustrates the calibration process with experimental data. Figure 3 in AN4247 shows the locus of
raw magnetometer measurements lying on the surface of the measurement ellipsoid. Figure 5 in AN4247
shows a partial solution with only the hard iron offset V removed. Finally Figure 6 shows the optimal
solution with both hard and soft iron effects removed resulting in the corrected measurements lying on the
surface of a sphere. The inverse soft iron matrix computed by the Freescale calibration software is shown
in Figure 4 of AN4247. Since this matrix is constrained to be symmetric, the transformation from original
ellipsoid to final sphere has proceeded by a shrink along the three principal axes, or eigenvectors, of the
initial measurement ellipsoid.
Calibration Algorithms and Source Code
6
This document has defined the calibration problem as the transformation of the locus of magnetometer
measurement from the surface of an ellipsoid displaced from the origin to the surface of a sphere located
at the origin. The algorithms and reference C source code which implement the calibration process are
available for license from Freescale for use free of charge in any product using a Freescale magnetometer.
Please contact your Freescale sales representative for details.
Calibrating an eCompass in the Presence of Hard and Soft Iron Interference, Rev. 0
8
Freescale Semiconductor
�
















 V2版本原理图(Capacitive-Fingerprint-Reader-Schematic_V2).pdf
V2版本原理图(Capacitive-Fingerprint-Reader-Schematic_V2).pdf 摄像头工作原理.doc
摄像头工作原理.doc VL53L0X简要说明(En.FLVL53L00216).pdf
VL53L0X简要说明(En.FLVL53L00216).pdf 原理图(DVK720-Schematic).pdf
原理图(DVK720-Schematic).pdf 原理图(Pico-Clock-Green-Schdoc).pdf
原理图(Pico-Clock-Green-Schdoc).pdf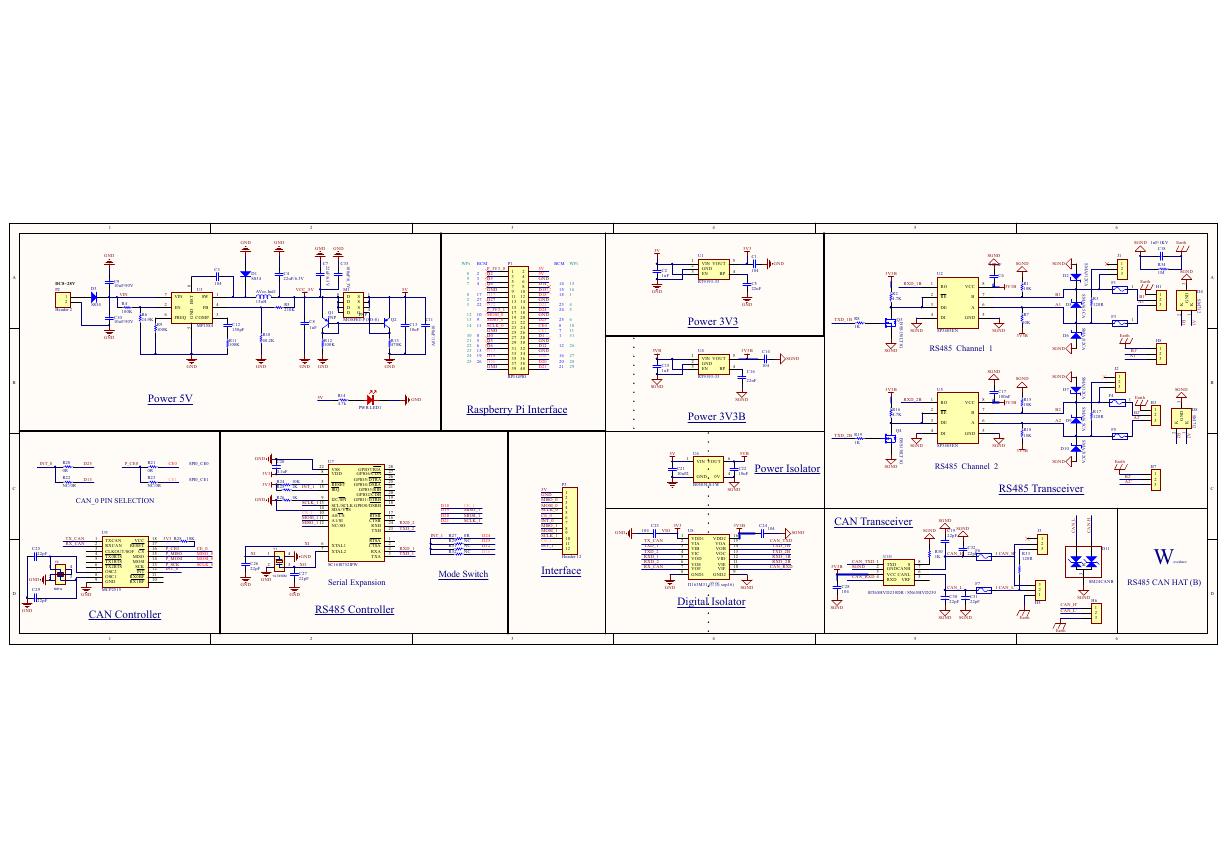 原理图(RS485-CAN-HAT-B-schematic).pdf
原理图(RS485-CAN-HAT-B-schematic).pdf File:SIM7500_SIM7600_SIM7800 Series_SSL_Application Note_V2.00.pdf
File:SIM7500_SIM7600_SIM7800 Series_SSL_Application Note_V2.00.pdf ADS1263(Ads1262).pdf
ADS1263(Ads1262).pdf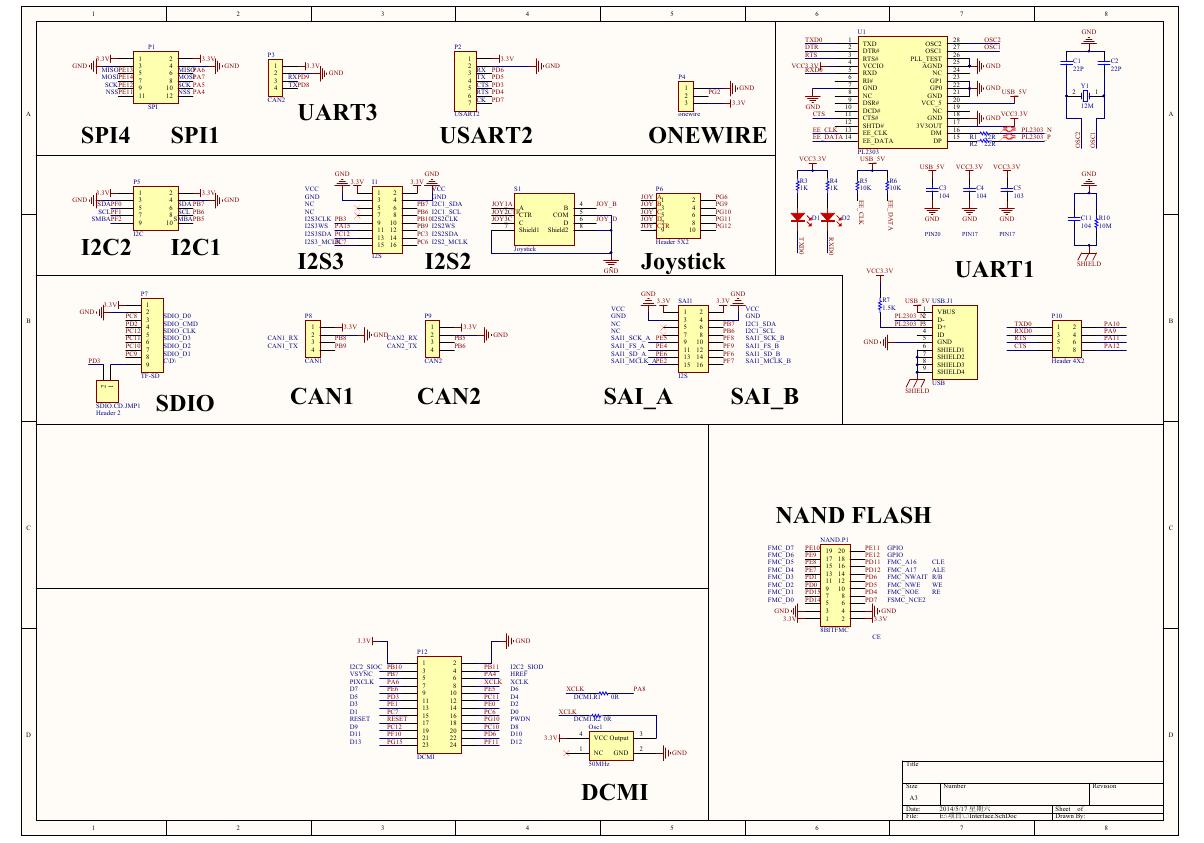 原理图(Open429Z-D-Schematic).pdf
原理图(Open429Z-D-Schematic).pdf 用户手册(Capacitive_Fingerprint_Reader_User_Manual_CN).pdf
用户手册(Capacitive_Fingerprint_Reader_User_Manual_CN).pdf CY7C68013A(英文版)(CY7C68013A).pdf
CY7C68013A(英文版)(CY7C68013A).pdf TechnicalReference_Dem.pdf
TechnicalReference_Dem.pdf