6-2-1 分数应用题（一）.学生版.doc-资料库

第1页 / 共7页

第2页 / 共7页

第3页 / 共7页

第4页 / 共7页

第5页 / 共7页

第6页 / 共7页

第7页 / 共7页

分数应用题（一）教学目标 1. 分析题目确定单位“1” 2. 准确找到量所对应的率，利用量÷对应率＝单位“1”解题 3. 抓住不变量，统一单位“1” 知识点拨一、知识点概述：分数应用题是研究数量之间份数关系的典型应用题，一方面它是在整数应用题上的延续和深化，另一方面，它有其自身的特点和解题规律．在解这类问题时，分析中数量之间的关系，准确找出“量”与“率”之间的对应是解题的关键．关键：分数应用题经常要涉及到两个或两个以上的量，我们往往把其中的一个量看作是标准量．也称为：单位“1”，进行对比分析。在几个量中，关键也是要找准单位“1”和对应的百分率，以及对应量三者的关系例如：（1）a 是 b 的几分之几，就把数 b 看作单位“1”． 1 8 （2）甲比乙多，乙比甲少几分之几？   ，因此乙比甲少 1 方法一：可设乙为单位“1”，则甲为 1 8 8 1   . 1 9 9 方法二：可设乙为 8 份，则甲为 9 份，因此乙比甲少 9 8 1 1   . 9 9 8 二、怎样找准分数应用题中单位“1” （一）、部分数和总数在同一整体中，部分数和总数作比较关系时，部分数通常作为比较量，而总数则作为标准量，那么总数就是单位“1”。例如：我国人口约占世界人口的几分之几？——世界人口是总数，我国人口是部分数，世界人口就是单位“1”。解答题关键：只要找准总数和部分数，确定单位“1”就很容易了。（二）、两种数量比较分数应用题中，两种数量相比的关键句非常多。有的是“比”字句，有的则没有“比”字，而是带有指向性特征的“占”、“是”、“相当于”。在含有“比”字的关键句中，比后面的那个数量通常就作为标准量，也就是单位“1”。例如：六（2）班男生比女生多——就是以女生人数为标准（单位“1”），解题关键：在另外一种没有比字的两种量相比的时候，我们通常找到分率，看“占”谁的，“相当于”谁的，“是”谁的几分之几。这个“占”，“相当于”，“是”后面的数量——谁就是单位“！”。（三）、原数量与现数量有的关键句中不是很明显地带有一些指向性特征的词语，也不是部分数和总数的关系。这类分数应用题的单位“1”比较难找。需要将题目文字完善成我们熟悉的类似带“比”的文字，然后在分析。例如：水结成冰后体积增加了，冰融化成水后，体积减少了。完善后：水结成冰后体积增加了→ “水结成冰后体积比原来增加了” →原来的水是单位“1” 冰融化成水后，体积减少了→ “冰融化成水后，体积比原来减少了” →原来的冰是单位 2-2-1.分数应用题（一）.题库学生版 page 1 of 7

“1” 解题关键：要结合语文知识将题目简化的文字丰富后在分析例题精讲模块一、单位“1”不变抓住量率对应进行计算【例 1】村里种了新瓜，男女老少品尝它．小伙每人吃一个，姑娘两人分一瓜；老人一瓜三人吃，四个小孩吃一瓜．男女老少四个组，一共吃了五十瓜，各组人数都相等，每组多少人品尝瓜？【例 2】五年级男生有 50 人，女生有 40 人．⑴女生人数是男生人数的几分之几？⑵男生人数比女生人数多几分之几？⑶女生人数比男生人数少几分之几？⑷女生比男生少的人数是全班人数的几分之几？【巩固】一个单位精简机构后有工作人员 120 人，比原来工作人员少 40 人，精简了几分之几？【例 3】将一个分数作如下图所示的变化后，得到的新分数比原分数减少的百分率等于 %。分子减少10% 分母增加50% 【例 4】根据图中的信息回答，剩下的糖果是原来糖果重量的。 2-2-1.分数应用题（一）.题库学生版 page 2 of 7

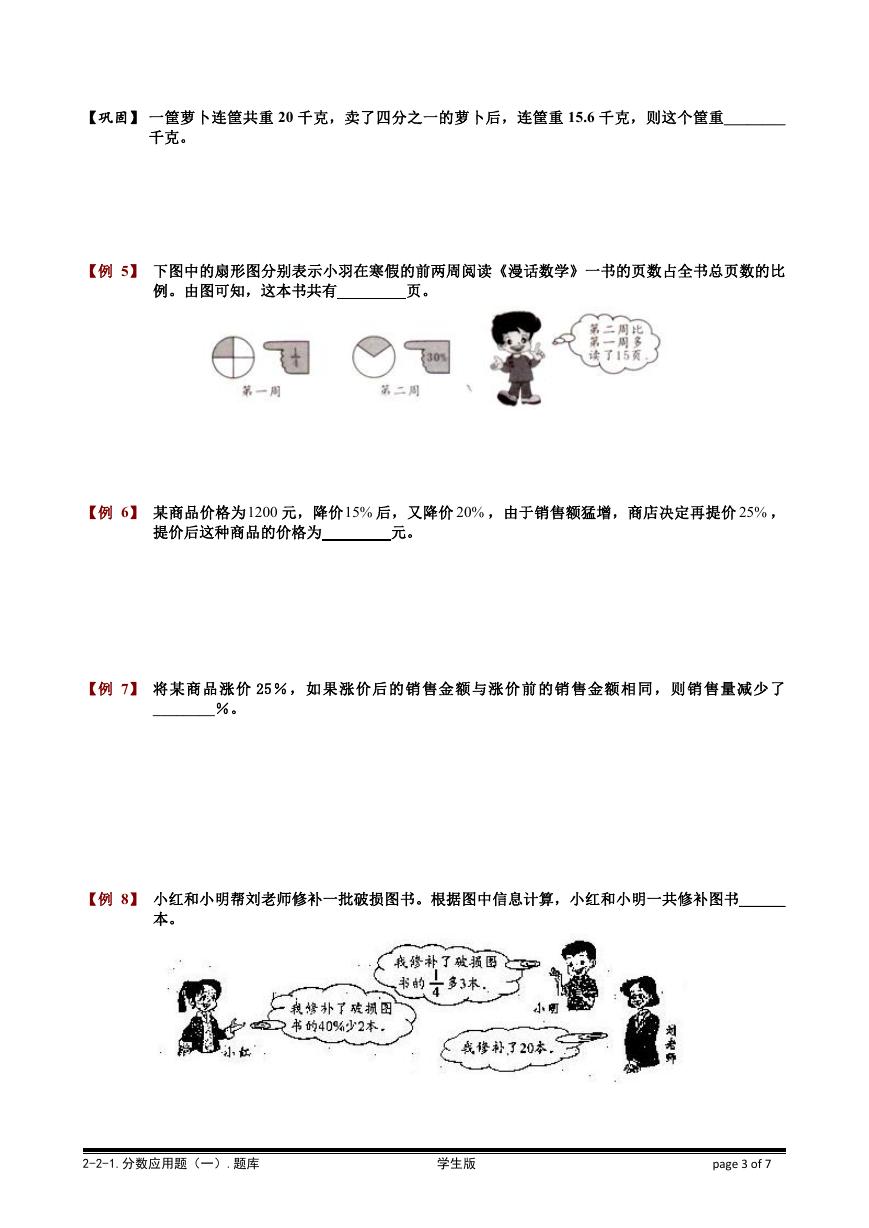
【巩固】一筐萝卜连筐共重 20 千克，卖了四分之一的萝卜后，连筐重 15.6 千克，则这个筐重________ 千克。【例 5】下图中的扇形图分别表示小羽在寒假的前两周阅读《漫话数学》一书的页数占全书总页数的比例。由图可知，这本书共有页。【例 6】某商品价格为1200 元，降价15% 后，又降价 20% ，由于销售额猛增，商店决定再提价 25% ，提价后这种商品的价格为元。【例 7】将某商品涨价 25％，如果涨价后的销售金额与涨价前的销售金额相同，则销售量减少了 ________％。【例 8】小红和小明帮刘老师修补一批破损图书。根据图中信息计算，小红和小明一共修补图书______ 本。 2-2-1.分数应用题（一）.题库学生版 page 3 of 7

【例 9】小静的书架上有三种不同种类的书，其中漫画书比故事书多 2 本，小说书比故事书少 2 本，已知故事书比小说书多 25% ，那么漫画书比故事书多百分之几？【巩固】一个水箱中的水是装满时的 5 6 ，用去 200 立升以后，剩余的水是装满时的 3 4 ，这个水箱的容积是多少立升？【巩固】水果店卖出库存水果的五分之一后，又运进水果 66000 斤，这时库存水果比原来库存量多六分之一，原来库存水果多少万斤？【巩固】迎春农机厂计划生产一批插秧机，现已完成计划的 56％，如果再生产 5040 台，总产量就超过计划产量的 16％．那么，原计划生产插秧机台．【例 10】已知小明家 2007 年总支出是 24300 元，各项支出情况如图所示，其中教育支出是______元. 【巩固】某项目的成本包括：人力成本、差旅费、活动费、会议费、办公费、招待费以及其他营运费用，它们所占比例如图所示，其中的活动费是 10320 元，则该项目的成本是元。 2-2-1.分数应用题（一）.题库学生版 page 4 of 7

【例 11】小强看一本书，每天看 15 页，4 天后加快进度，又看了全书的 2 5 ，还剩下 30 页，这本故事书有多少页？【巩固】一个水箱中的水是装满时的 5 6 ，用去 200 立升以后，剩余的水是装满时的 3 4 ，这个水箱的容积是多少立升？【巩固】小强看一本故事书，每天看 20 页，5 天后还剩下全书的 1 5 没看，这本故事书有多少页？【巩固】点点暑假练习写字，每天写 3 页，5 天后加快速度又写了全部的 1 5 ，还剩下 25 页，点点共练习多少页？【例 12】用一批纸装订一种练习本．如果已装订 120 本，剩下的纸是这批纸的 40％；如果装订了 185 本，则还剩下 1350 张纸．这批纸一共有多少张? 【例 13】有男女同学325 人，新学年男生增加 25 人，女生减少 1 20 ，总人数增加16 人，那么现有男同学多少人？【例 14】菜地里黄瓜得到丰收，收下全部的 3 8 装满 8 筐，求共收黄瓜多少千克？时，装满了 4 筐还多 36 千克，收完其余的部分时，又恰好【巩固】菜地里的西红柿获得丰收，摘了全部的 2 5 满 6 筐，则共收得西红柿_______千克．时，装满了 3 筐还多16 千克．摘完其余部分后，又装 2-2-1.分数应用题（一）.题库学生版 page 5 of 7

【巩固】菜园里西红柿获得丰收，收下全部的 3 8 满 6 筐，求共收西红柿多少千克？时，装满 3 筐还多 24 千克，收完其余部分时，又刚好装【例 15】一本书，已看了130 页，剩下的准备 8 天看完．如果这 8 天每天看的页数相等，而且 3 天看的页数恰好是全书的 5 22 ，这本书共有多少页？【例 16】李大娘把养的鸡分别关在东、西两个院内．已知东院养鸡 40 只；现在把西院养鸡总数的 1 4 卖给卖给加工厂，再把剩下的鸡与东院全部的鸡相加，其和恰好等于原来东、西两院养鸡商店， 1 3 总数的 50％.原来东、西两院一共养鸡多少只? 【例 17】某运输队运一批大米．第一天运走总数的 1 5 袋没有运走．这批大米原来一共有多少袋？多 60 袋，第二天运走总数的 1 4 少 60 袋．还剩下 220 【巩固】京京看一本故事书，第一天看了全书的 1 8 还多 21 页，第二天看了全书的 1 6 少 6 页，还剩 172 页，这本故事书一共有多少页？【例 18】春天幼儿园中班小朋友的平均身高是 115 厘米，其中男孩比女孩多 1 5 10% ，这个班男孩的平均身高是厘米．，女孩平均身高比男孩高 2-2-1.分数应用题（一）.题库学生版 page 6 of 7

【例 19】我国某城市煤气收费规定：每月用量在 8 立方米或 8 立方米以下都一律收 6.9 元，用量超过 8 立方米的除交 6.9 元外，超过部分每立方米按一定费用交费，某饭店 1 月份煤气费是 82.26 元，8 月份煤气费是 40.02 元，又知道 8 月份煤气用量相当于1 月份的 7 ，那么超过 8 立方米后，每立方 15 米煤气应收多少元？【例 20】一次数学竞赛均是填空题,小明答错的恰是题目总数的 1 4 ,小亮答错 5 题，两人都答错的题目占总题数的 1 6 .已知小明、小亮都答对的题目数超过了试题总数的一半，问他们都答对多少题? 【例 21】甲、乙二人欲买一件商品，按照标价，甲带的钱差 40 元，乙带的钱少 1 4 9 折购买，于是他们合买了一件，结果剩下 28 元．这件商品标价为多少元？．经过讨价最后可以按【例 22】箱子里装有若干个相同数量的黑球和白球，现往箱子里再放入 14 个球(只有黑球和白球)，这时黑球数量占球的总数的，那么现在箱子里有________个白球。 1 6 2-2-1.分数应用题（一）.题库学生版 page 7 of 7

资料库

6-2-1 分数应用题（一）.学生版.doc

相关推荐

小学奥数

热门标签

最新资料