第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
第五讲 算式迷宫.doc
第五讲 算式迷
小朋友们？你猜过算式迷吗？算式迷是由一些数字与算式构成
的。日本人形象地称之为“虫食算”，即算式中一些数字被虫子咬去
了。要想猜出算式迷，也得先分析这些数字和算式构成的“谜面”，
再运用一些推理方法找到“谜底”。
典型例题
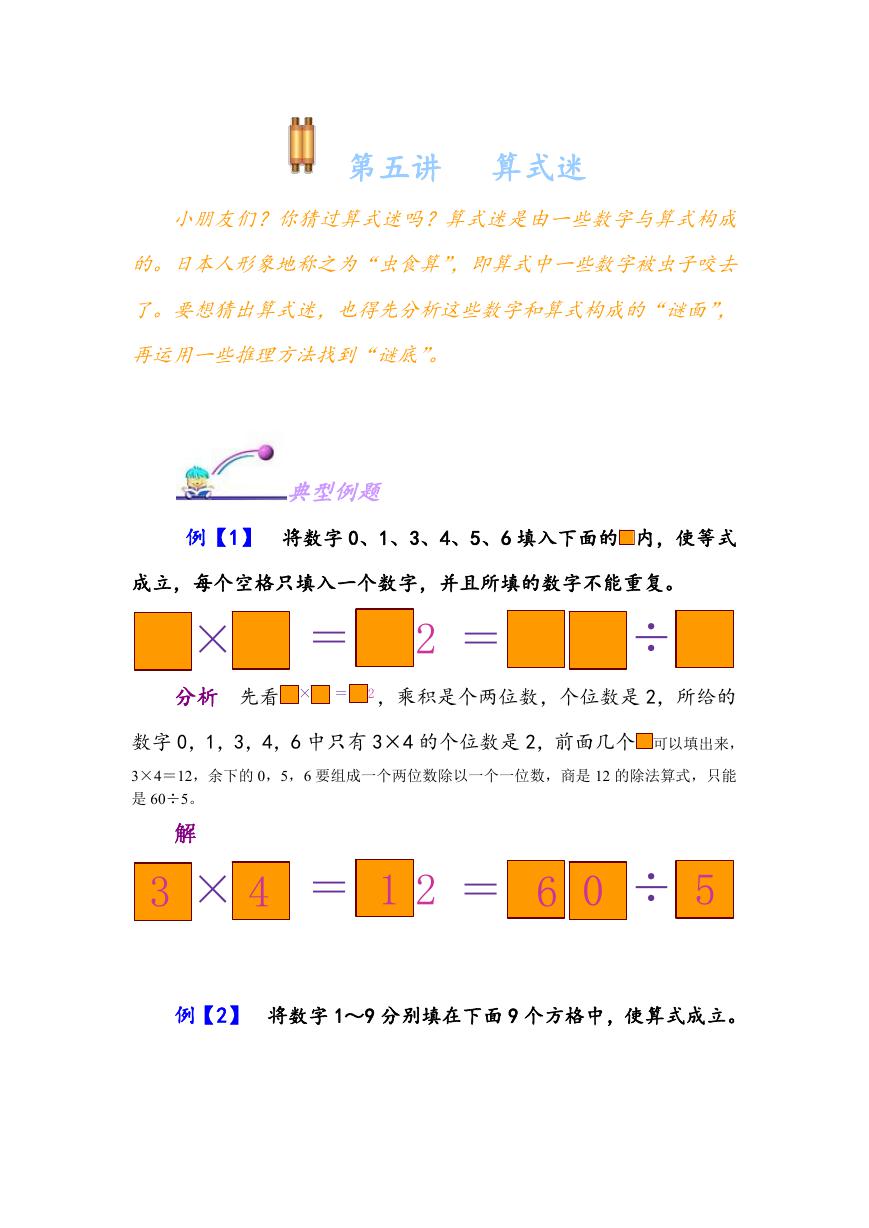
例【1】 将数字 0、1、3、4、5、6 填入下面的 内，使等式
成立，每个空格只填入一个数字，并且所填的数字不能重复。
× ＝ 2 ＝
÷
分析 先看 × ＝ 2 ，乘积是个两位数，个位数是 2，所给的
数字 0，1，3，4，6 中只有 3×4 的个位数是 2，前面几个 可以填出来，
3×4＝12，余下的 0，5，6 要组成一个两位数除以一个一位数，商是 12 的除法算式，只能
是 60÷5。
解
3
× ＝ 2 ＝
1
4
6 0
÷
5
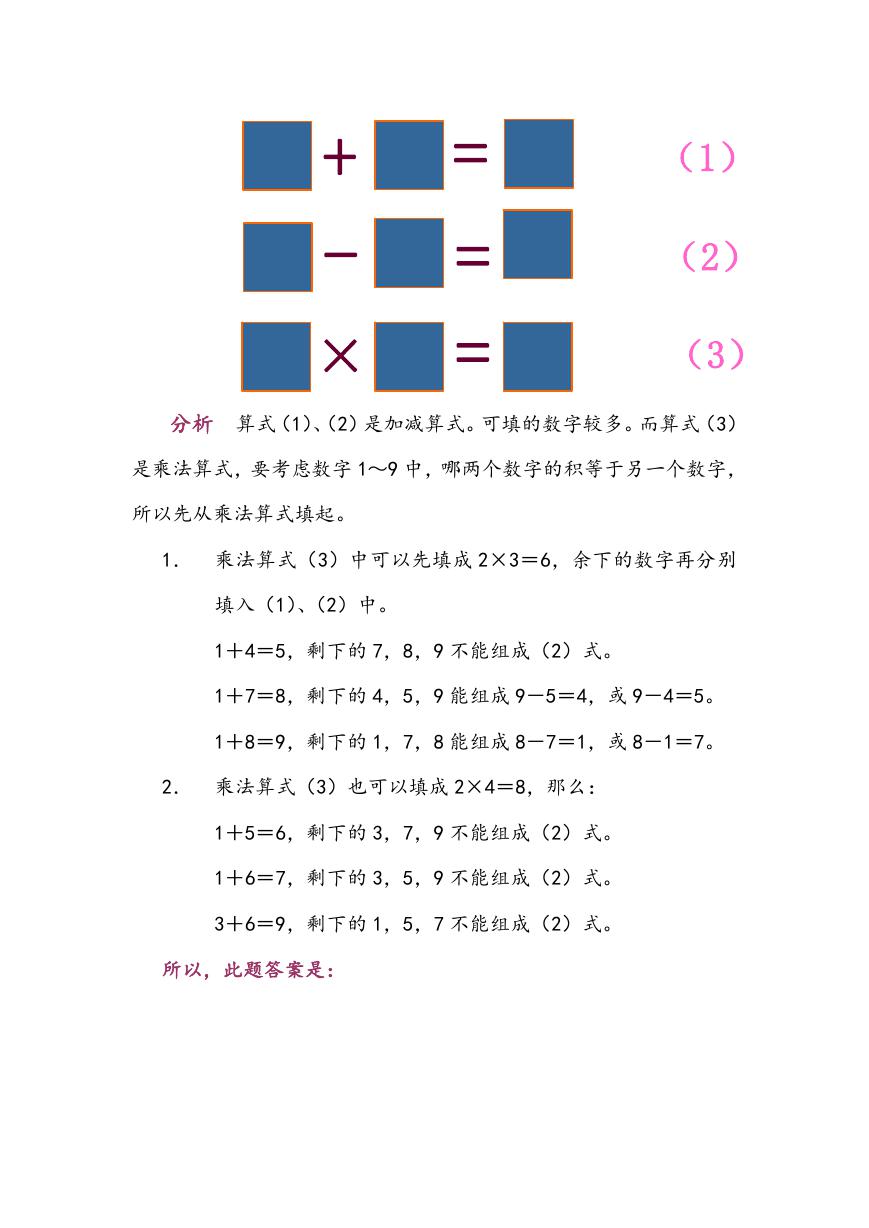
例【2】 将数字 1～9 分别填在下面 9 个方格中，使算式成立。
+
-
×
=
=
=
（1）
（2）
（3）
分析 算式（1）、（2）是加减算式。可填的数字较多。而算式（3）
是乘法算式，要考虑数字 1～9 中，哪两个数字的积等于另一个数字，
所以先从乘法算式填起。
1． 乘法算式（3）中可以先填成 2×3＝6，余下的数字再分别
填入（1）、（2）中。
1＋4＝5，剩下的 7，8，9 不能组成（2）式。
1＋7＝8，剩下的 4，5，9 能组成 9－5＝4，或 9－4＝5。
1＋8＝9，剩下的 1，7，8 能组成 8－7＝1，或 8－1＝7。
2． 乘法算式（3）也可以填成 2×4＝8，那么：
1＋5＝6，剩下的 3，7，9 不能组成（2）式。
1＋6＝7，剩下的 3，5，9 不能组成（2）式。
3＋6＝9，剩下的 1，5，7 不能组成（2）式。
所以，此题答案是：
1
2
1
9
2
4
8
2
7
4
3
5
7
3
8
（或
5
9
5
＝
4
）
6
9
1
（或
8
1
＝
7
）
6
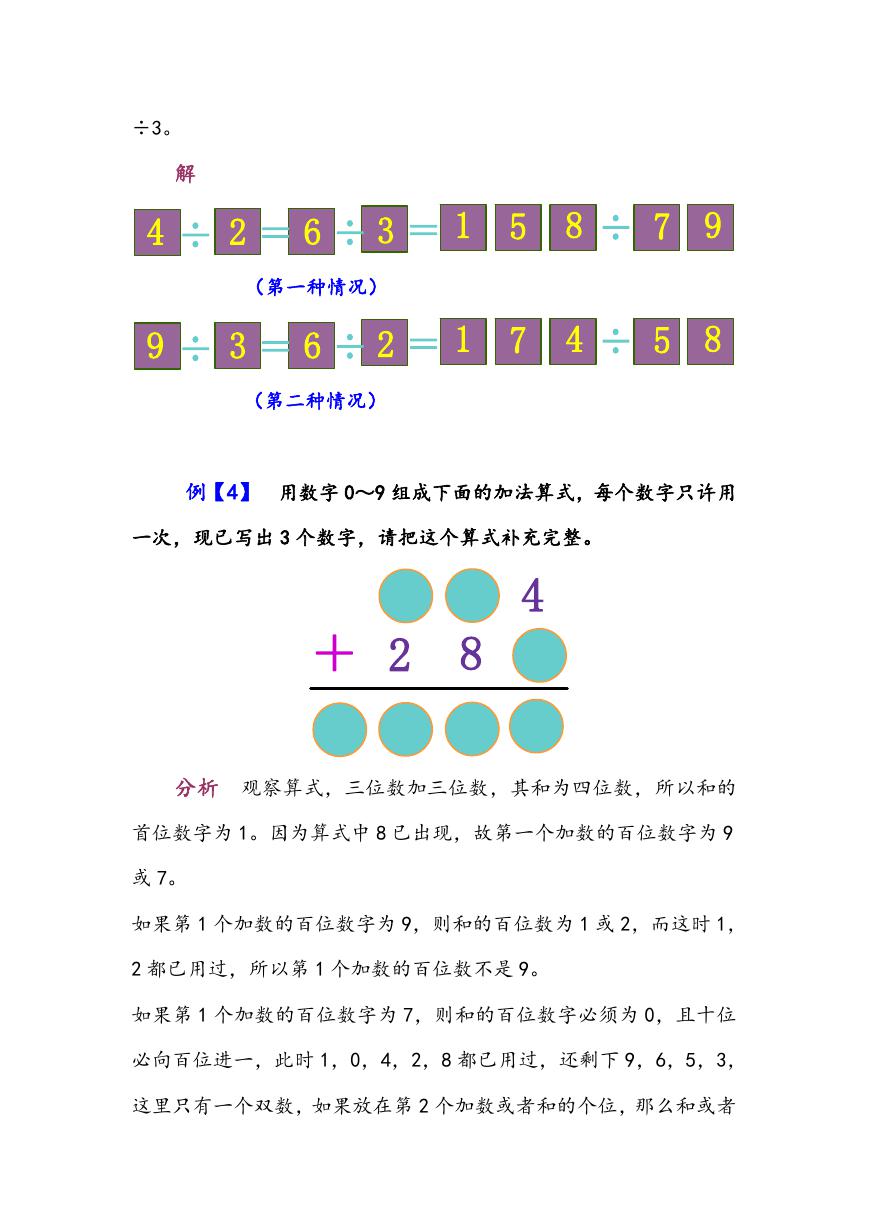
例【3】 把数字 1～9 填在方格里，使等式成立，每个数字只
能用一次。
÷ ＝ ÷ ＝
÷
分析 一位数组成除法算式商相等的情况：4÷2＝6÷3，6÷2
＝9÷3，8÷2＝4÷1，所以可先填写等式中的前 4 个数。如果先填 4
÷2＝6÷3，剩下的 1，5，7，8，9 要组成一个三位数除以一个两位
数，商是 23 即 ×2 ＝
，所得的积的个位一定是个双数，只
能填 8。试验可知：79×2＝158。如果先填 8÷2 ＝4÷1，剩下的 3，
5，6，7，9 不能组成一个三位数除以一个两位数、商是 4 的除以算
式，所以等式中的前 4 个数不能填 8÷2＝4÷1。我们可以填 4÷2＝6
÷3。
解
4
9
÷ ＝ ÷ ＝
3
2
6
（第一种情况）
÷ ＝ ÷ ＝
2
3
6
1
1
5
7
8
÷
7 9
4
÷
5 8
（第二种情况）
例【4】 用数字 0～9 组成下面的加法算式，每个数字只许用
一次，现已写出 3 个数字，请把这个算式补充完整。
4
＋
2
8
分析 观察算式，三位数加三位数，其和为四位数，所以和的
首位数字为 1。因为算式中 8 已出现，故第一个加数的百位数字为 9
或 7。
如果第 1 个加数的百位数字为 9，则和的百位数为 1 或 2，而这时 1，
2 都已用过，所以第 1 个加数的百位数不是 9。
如果第 1 个加数的百位数字为 7，则和的百位数字必须为 0，且十位
必向百位进一，此时 1，0，4，2，8 都已用过，还剩下 9，6，5，3，
这里只有一个双数，如果放在第 2 个加数或者和的个位，那么和或者
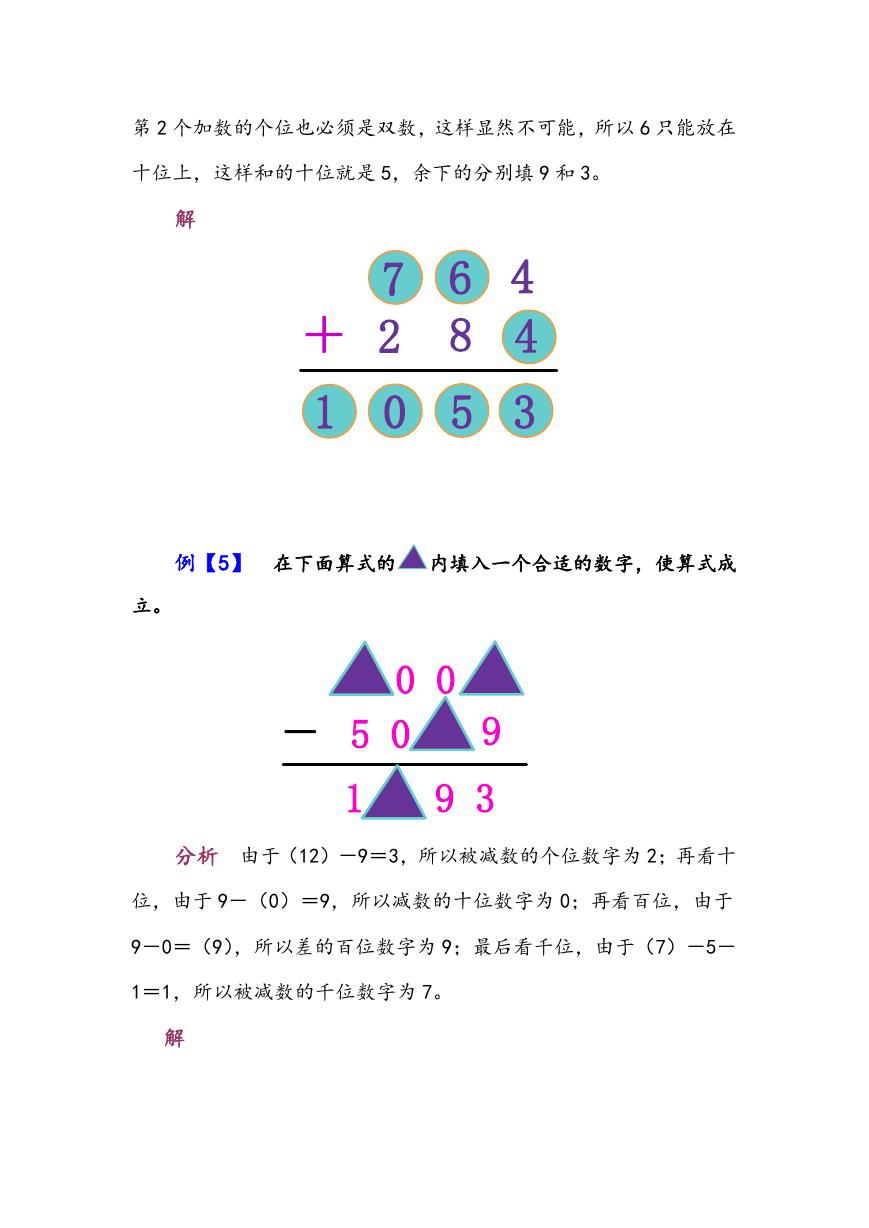
第 2 个加数的个位也必须是双数，这样显然不可能，所以 6 只能放在
十位上，这样和的十位就是 5，余下的分别填 9 和 3。
解
7 6
8
2
＋
1
0 5
4
4
4
4
3
例【5】 在下面算式的 内填入一个合适的数字，使算式成
立。
0 0
－
5 0
9
1
9 3
分析 由于（12）－9＝3，所以被减数的个位数字为 2；再看十
位，由于 9－（0）＝9，所以减数的十位数字为 0；再看百位，由于
9－0＝（9），所以差的百位数字为 9；最后看千位，由于（7）－5－
1＝1，所以被减数的千位数字为 7。
解
－
7
5 0
0 0
0
2
9
1
9
9 3
小结 在做算式迷这类题时，首先要观察题目
中的算式，看看它含有哪几种运算，要填的数是几位数，要填的数字
是否规定好了，还是可以任意填。其次是要熟练运用加减之间、乘除
之间的逆运算关系进行推理。先确定能够确定的数字，而且每一步要
把确定的结果代入算式，以利于下面的推理。最后，所有的空格填完
之后要检验一下，看看答案是否正确。
相关推荐
V2版本原理图(Capacitive-Fingerprint-Reader-Schematic_V2).pdf
摄像头工作原理.doc
VL53L0X简要说明(En.FLVL53L00216).pdf
原理图(DVK720-Schematic).pdf
原理图(Pico-Clock-Green-Schdoc).pdf
原理图(RS485-CAN-HAT-B-schematic).pdf
File:SIM7500_SIM7600_SIM7800 Series_SSL_Application Note_V2.00.pdf
ADS1263(Ads1262).pdf
原理图(Open429Z-D-Schematic).pdf
用户手册(Capacitive_Fingerprint_Reader_User_Manual_CN).pdf
CY7C68013A（英文版）(CY7C68013A).pdf
TechnicalReference_Dem.pdf
