第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
2021-2022学年天津市南开区七年级上册期末数学试卷及答案.doc
2021-2022 学年天津市南开区七年级上册期末数学试卷及答
案
一、选择题：本大题共 12 小题，每道题 3 分，共 36 分，在每小题给出的四个选项中，只有
一个项是符合题目要求的。
1. 已知 A 地的海拔高度为-36 米，B 地比 A 地高 20 米，则 B 地的海拔高度为（）
A. 16 米
【答案】C
B. 20 米
C. -16 米
D. -56 米
2. 在数 ( 3)
，0，
2
( 3) ， 9 ， 41 中，正数的个数为（）
A. 2
【答案】B
B. 3
C. 4
D. 5
3. 据 Worldmeters 实时统计数据显示，截至北京时间 2021 年 10 月 3 日，全球累计确诊新
冠肺炎病例约达 235000000 例，数据 235000000 用科学记数法表示为（
）
A. 2.35×108
B. 2.35×109
C. 235×106
D.
0.235×109
【答案】A
2
5
4. 单项式﹣
A. ﹣
2
5
，3
【答案】C
a3b 的系数与次数分别是（
）
B.
2
5
，4
C. ﹣
2
5
，4
D. ﹣2，3
5. 如图，虚线左边的图形绕虚线旋转一周，能形成的几何体是（）
A.
B.
C.
D.
【答案】B
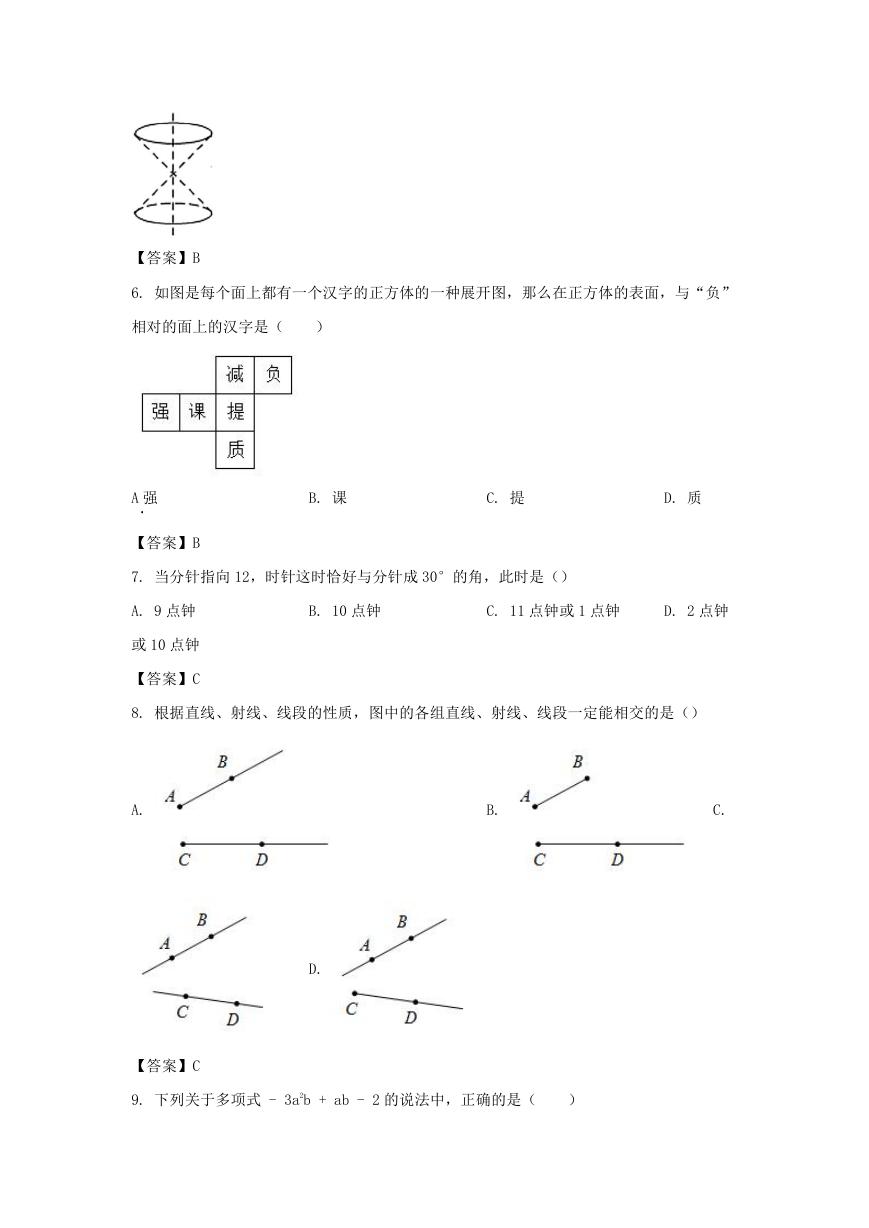
6. 如图是每个面上都有一个汉字的正方体的一种展开图，那么在正方体的表面，与“负”
相对的面上的汉字是（
）
A.强
【答案】B
B. 课
C. 提
D. 质
7. 当分针指向 12，时针这时恰好与分针成 30°的角，此时是（）
B. 10 点钟
C. 11 点钟或 1 点钟
D. 2 点钟
A. 9 点钟
或 10 点钟
【答案】C
8. 根据直线、射线、线段的性质，图中的各组直线、射线、线段一定能相交的是（）
A.
B.
C.
D.
【答案】C
9. 下列关于多项式 - 3a2b + ab - 2 的说法中，正确的是（
）
A. 是二次三项式
C. 常数项是 2
【答案】D
B. 二次项系数是 0
D. 最高次项是 - 3a2b
10. 一种商品每件成本为 a 元，原来按成本增加 40%定出售价，现在由于库存积压减价，打
八折出售，则每件盈利（
）元．
A. 0.1a
【答案】B
B. 0.12a
C. 0.15a
D. 0.2a
11. 用式子表示“比 x 的 3 倍小 5 的数等于 x 的 4 倍”为（
1
3
B. 5﹣3x＝4x
A. 3x﹣5＝4x
C.
）
x﹣5＝4x
D. 3x﹣5
＝
x
1
4
【答案】A
12. 如图． AOB a
， 1OA 、 1OB 分别是∠AOM 和∠MOB的平分线， 2OA 、 2OB 分别是
1AOM
和
1MOB
的平分线， 3OA 、 3OB 分别是 2A OM
和
2MOB
的平分线，…， nOA 、
分别是
1nA OM
和
1nMOB
的平分线，则 n
A OB
n
的度数是（）
A.
a
n
【答案】C
B.
a
12n
C.
a
2n
D.
a
2
n
二、填空题：本大题共 6 小题，每小题 3 分，共 18 分，请将答案直接填在答题纸中对应的
横线上．
13. 已知∠1 与∠2 互余，∠3 与∠2 互余，则∠1_____∠3．（填“＞”，“＝”或“＜”）
【答案】＝
14. 若 1 58 37
【答案】102 32
， 2
43 55
，则 1
______．
2
15. 若点 C 是直线 AB 上的一点，且线段 AC=3，BC=7，则线段 AB 的长为______．
【答案】10 或 4
16. 已知|m|＝m+1，则（4m﹣1）4＝___．
【答案】81
17. 古书《九章算术》有这样一个问题：“今有共买鸡，人出九，盈十一；人出六，不足十
六，问人数、鸡价各几何？”大意是：有几个人共同出钱买鸡，每人出 9 钱，则多了 11 钱，
每人出 6 钱，则少了 16 钱，那么有几个人共同买鸡？鸡的总价是多少？若有 x 个人共同买
鸡，则可列方程：_________．
【答案】9x-11=6x+16
18. 有若干个数，第一个数记为 1a ，第二个数记为 2a ，…，第 n 个数记为 na ．若 1
a ，
1
2
从第二个数起，每个数都等于“1 与它前面那个数的差的倒数”， 2021a
______．
【答案】
2
3
三、解答题（共 46 分）
19. （1）解方程：3
3
（2）解方程：
x
1 2
x
x
4
1
x
6
x ；（2）
【答案】（1）
3
4
x ．
3
5
（1）先移项，再合并同类项，最后化系数为 1；
（2）先去分母，再移项，合并同类项，最后化系数为 1．
【详解】解：（1）3x﹣1＝2﹣x
4x＝3
3
4
x
（2）
x
6
3
x
4
1
2x－9＋3x＝-12
5x＝-3
3
5
x ．
20. 已知代数式 A =- 6x2y + 4xy2 - 5，B =- 3x2y + 2xy2 - 3．
（1）求 A - B 的值，其中|x - 1| + （y+2）2 = 0．
（2）请问 A - 2B 的值与 x，y 的取值是否有关系，试说明理由．
【答案】（1）12；（2） 2A
B 的值与 x，y 的取值没有关系，理由见解析．
（1）先计算 A B 的值，再由
x
1
y
2
2
（2）计算 2A
B 的值，即可得到答案．
得到 x 1, y
0
，代入 A B 计算即可；
2
【详解】解：（1）∵
A
2
4
xy
，
5
B
3
2
x y
2
2
xy
3
∴
A B
6
2
x y
2
4
xy
2
3
x y
2
2
xy
3
6
2
x y
5
6
2
x y
2
4
xy
5 3
2
x y
2
2
xy
3
= 3
2
x y
2
2
xy
2
∵
x
1
y
2
2
，
0
x
1
0,
y
2
2
0
∴ 1 0, +2=0
x
y
∴ x 1, y
2
∴
A B
2
3 1
2 1
2
2
2
2 6 8 2 12
（2） 2A
B 的值与 x，y 的取值没有关系，理由如下：
A
2
B
6
2
x y
4
xy
2
5 2
3
2
x y
2
xy
2
3
6
2
x y
2
4
xy
5 6
2
x y
2
4
xy
6 1
B 的值与 x，y 的取值没有关系．
∴ 2A
21. 已知一个角的余角比这个角的补角的一半还小12 ，求这个角的度数．
【答案】24°
设这个角的度数为 x 度，则余角是（90-x）度，补角是（180-x）度，根据个角的余角比这
个角的补角的一半还少 12°即可列方程求解．
【详解】解：设这个角的度数为 x 度，根据题意，得：
90-x=
1
2
（180-x）-12，
解得
x=24．
∴这个角的度数为 24°．
22. 已知：线段 AB＝20cm，点 C 为线段 AB 上一点，BC＝4cm，点 D、点 E 分别为 AC 和 AB
的中点，求线段 DE 的长．
【答案】2cm
先根据线段的和差，可得 AC 的长，再根据线段中点的性质，可得 AD、AE 的长，最后根据线
段的和差，可得 DE 的长．
【详解】解：由线段的和差，得
AC＝AB﹣BC＝20﹣4＝16cm，
由点 D 是 AC 的中点，
所以
AD
1
2
AC
1 16 8
2
cm；
由点 E 是 AB 的中点，得
AE
1
2
AB
1 20 10
2
cm，
由线段的和差，得
DE＝AE﹣AD＝10﹣8＝2cm．
23. 甲、乙两人从 A，B 两地同时出发，甲骑自行车，乙开汽车，沿同一条路线相向匀速行．
出发后经 3 小时两人相遇．已知在相遇时乙比甲多行了 90 千米，相遇后经 1 小时乙到达 A
地问：
（1）甲车速度是________千米/小时，乙车速度是_________千米/小时．A，B 距离是_______
千米．
（2）这一天，若乙车晚 1 小时出发，则再经过多长时间，两车相距 20 千米？
【答案】（1）15，45，180；（2）
29
12
小时或
37
12
小时
（1）设甲的速度为 xkm/h，根据出发后经 3 小时两人相遇列出方程，解之即可；
（2）设再经过 y 小时，两人相距 20km，根据两车相距 20 千米分相遇前和相遇后分别列出
方程，解之即可．
【详解】解：（1）设甲的速度为 xkm/h，则乙的速度为
90
3
x
3
=x+30（km/h），
根据题意得：
3x=x+30，
解得：x=15，
∴x+30=45，
∴AB 的距离为：45×4=180km，
∴AB 的距离为 180km；
（2）设再经过 y 小时，两人相距 20km，
则 15（y+1）+45y=180-20 或 15（y+1）+45y=180+20，
解得：y=
∴再经过
29
12
29
12
或
37
12
，
小时或
37
12
小时后，两人相距 20km．
24. 已知：如图 1，点 O 为直线 AB 上一点，过点 O 作射线 OC，使∠AOC：∠BOC＝1：5．将
一等腰直角三角板的直角顶点放在点 O 处，一直角边 ON 在射线 OB 上，另一直角边 OM 在直
线 AB 的下方．
（1）将图 1 中的等腰直角三角板绕点 O 以每秒 3°的速度逆时针方向旋转一周，直角边 ON
旋转后的对应边为 ON'，直角边 OM 旋转后的对应边为 OM'．在此过程中，经过 t 秒后，OM'
恰好平分∠BOC，求 t 的值；
（2）如图 2，在（1）问的条件下，若等腰直角三角板在转动的同时，射线 OC 也绕点 O 以
每秒 4°的速度顺时针方向旋转，射线 OC 旋转后的对应射线为 OC'．当射线 OC'落在射线 OC
的反向延长线上时，射线 OC 和等腰直角三角板同时停止运动．在此过程中，是否存在某一
时刻 t，使得 OC'//M'N'．若存在，请求出 t 的值，若不存在，诮说明理由；
（3）如图 3，在（1）问的条件下，若等腰直角三角板在转动的同时，射线 OC 也绕点 O 以
每秒 5°的速度顺针方向旋转，射线 OC 旋转后的对应射线为 OC'．当等腰直角三角板停止运
动时，射线 OC 也停止运动．在整个运动过程中．经过 l 秒后，∠M'ON'的某一边恰好平分
∠AOC'，请直接写出所有满足条件的 t 的值．
【答案】（1）55；（2）15 或
285
7
；（3）t=30 或
690
11
（1）当 OM'恰好平分∠BOC 时，OM'需要旋转 90°＋
或
1
2
870
11
或
1230
11
∠BOC＝165°，进而求解；
（2）第一种情况：当 OC'∥M'N'时，∠C’OM’＝∠OM’ N’＝45°，进而求解；第二种情
况：当 OC'∥M'N'时，∠C’OM’＝∠OM’ N’＝45°，进而求解；
（3）分四种情况：①当 ON’平分∠AOC’，且 ON’在直线 AB 上方时，②当 ON’平分∠AOC’，
且 ON’在直线 AB 下方时，③当 OM’平分∠AOC’，且 OM’在直线 AB 上方时，④当 OM’平
分∠AOC’，且 OM’在直线 AB 下时，分别画出图形，即可求解．
【详解】解：（1）设∠AOC＝x，则∠BOC＝5x，x＋5x＝180°，
∴∠AOC＝30°，则∠BOC＝150°．
当 OM'恰好平分∠BOC 时，
1
2
∠BOC＝165°，
OM'需要旋转 90°＋
165°÷3＝55，
所以，t＝55；
（2）第一种情况：
当 OC'∥M'N'时，
∠C’ON’＝∠ON’M’＝45°，
此时 t＝（150°−45°）÷（3°＋4°）＝15，
第二种情况：
当 OC'∥M'N'时，
∠C’OM’＝∠OM’ N’＝45°，
此时 t＝（240°＋45°）÷（3°＋4°）＝
285
7
；
（3）分四种情况：
①当 ON’平分∠AOC’，且 ON’在直线 AB 上方时，
则 2∠AON’＝∠AOC’，即 2(180°−3t)＝（30°＋5t），解得：t＝30，
②当 ON’平分∠AOC’，且 ON’在直线 AB 下方时，
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
