第1页 / 共4页
第2页 / 共4页
第3页 / 共4页
第4页 / 共4页
第一讲 一笔画问题.doc
第一讲 一笔画问题
小朋友们，你们能把下面的图形一笔画出来吗？
如果用笔在纸上连续不断又不重复，一笔画成某种图形，这种图
形就叫一笔画。那么是不是所有的图形都能一笔画成呢？这一讲我们
就一起来学习一笔画的规律。
典型例题
例【1】 下面这些图形，哪个能一笔画？哪个不能一笔画？
（1）
（2）
（3）
（4）
分析 图（1）一笔画出，可以从图中任意一点开始画该图，画
到同一点结束。
经过尝试后，可以发现图（2）不能一笔画出。
图（3）不是连通的，显然也不能一笔画出。图（4）也可以一笔
画出，且从任何一点出发都可以。
通过观察，我们可以发现一个几何图形中和一点相连通的线的条
数不同。由一点发出有偶数条线，那么这个点叫做偶点。相应的，由
一点出发有奇数条数，则这个点叫做奇点。
再看图（1）、（4），其中每一点都是偶点，都可以一笔画，且可
以从任意一点画起。而图（2）有 4 个奇点，2 个偶点，不能一笔画
成。
这样我们发现，一个图形能否一笔画和这个图形奇点，偶点的个
数有某种联系，到底存在什么样的关系呢，我们再看一个例题。
例【2】 下面各图能否一笔画成？
（1）
（2）
（3）
分析 图（1）从任意一点出都可以一笔画成，因为它的每一个
点都是与两条线相连的偶点。
关于图（2），经过反复试验，也可找到画法：由 A
B
C
A
D
C。图中 B、D 为偶点，A、C 为奇点，即图中有两个奇点，两
个偶点。要想一笔画，需从奇点出发，回到奇点。
经过尝试，图（3）无法一笔画成，而图中有 4 个奇点，5 个偶点。
解 图（1）、（2）可以一笔画。
这样我们可以发现能否一笔画和奇点、偶点的数目有着紧密的关
系。
如果图形只有偶点，可以以任意一点为起点，一笔画出。如果只
有两个奇点，也可以一笔画出，但必须从奇点出发，由另一点结束。
如果图形的奇点个数超过两个，则图形不能一笔画出。
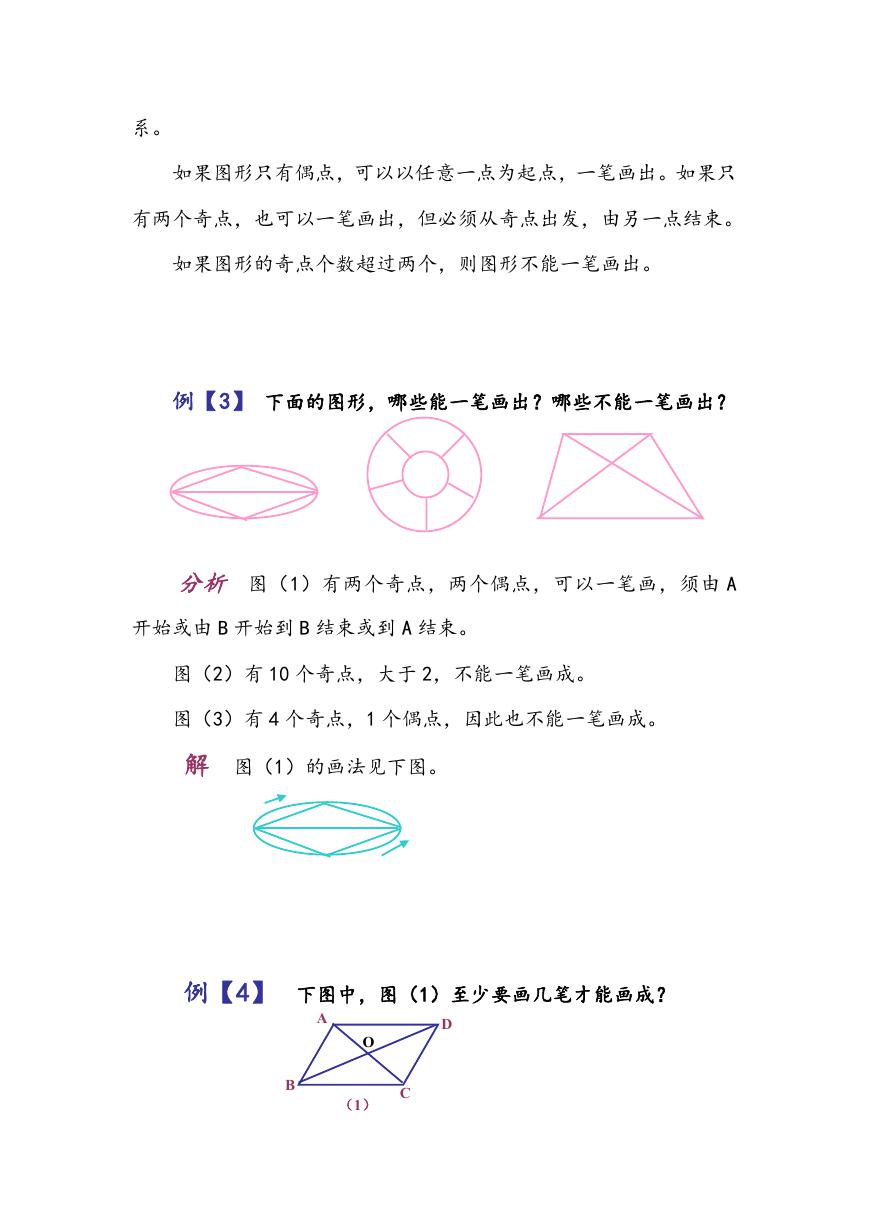
例【3】 下面的图形，哪些能一笔画出？哪些不能一笔画出？
分析 图（1）有两个奇点，两个偶点，可以一笔画，须由 A
开始或由 B 开始到 B 结束或到 A 结束。
图（2）有 10 个奇点，大于 2，不能一笔画成。
图（3）有 4 个奇点，1 个偶点，因此也不能一笔画成。
解 图（1）的画法见下图。
例【4】 下图中，图（1）至少要画几笔才能画成？
A
O
D
B
C
（1）
分析 图（1）有 4 个奇点，所以不能一笔画出。如果把它分成
几个部分，而每个部分是一笔画图形，则我们就可以用最少的几笔画
出这个图形。按照这样的要求，每个部分最多含有两个奇点，可以采
用再两个奇点之间增加一条或者去掉一条线的方法，该奇点就变成偶
点。经观察，图（1）可以切分成图（A）、（B）两个图形。这两部分
都可以一笔画出，所以图（1）至少用两笔画出。
解 将图（1）分成图（A）、（B），则图（A）可由 A-B-O-D-A-C-D
一笔画成，图（B）由 B-C 一笔画成，所以图（1）至少要两笔画完。
A
O
D
A
D
O
B
C
（1）
B
C
（A）
B
（B）
C
小结 能否一笔画成，关键在于判别奇点、偶点的
个数。
一、 只有偶点，可以一笔画，并且可以以任意一点作为起点。
二、 只有两个奇点，可以一笔画，但必须以这两个奇点分别作为起
点和终点。
三、 奇点超过两个，则不能一笔画。对于一些比较复杂的路线问题，
可以先转化为简单的几何图形，然后根据判定是否能一笔画的
方法进行解答。
相关推荐
V2版本原理图(Capacitive-Fingerprint-Reader-Schematic_V2).pdf
摄像头工作原理.doc
VL53L0X简要说明(En.FLVL53L00216).pdf
原理图(DVK720-Schematic).pdf
原理图(Pico-Clock-Green-Schdoc).pdf
原理图(RS485-CAN-HAT-B-schematic).pdf
File:SIM7500_SIM7600_SIM7800 Series_SSL_Application Note_V2.00.pdf
ADS1263(Ads1262).pdf
原理图(Open429Z-D-Schematic).pdf
用户手册(Capacitive_Fingerprint_Reader_User_Manual_CN).pdf
CY7C68013A（英文版）(CY7C68013A).pdf
TechnicalReference_Dem.pdf
