第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
2021-2022学年山东省潍坊市诸城市八年级下学期期中数学试题及答案.doc
2021-2022 学年山东省潍坊市诸城市八年级下学期期中数学试题及答
一、选择题（本题共 8 小题，每小题 4 分，共 32 分，在每个小题给出的四个选项中，只有一项是符合题目
案
第Ⅰ卷（选择题，52 分）
要求的）
1. 若 3
1
3
A. x≥
1x 在实数范围内有意义，则 x的取值范围是（）
B. x≤
1
3
C. x＞
1
3
D. x≠
1
3
2. 下列各数 π ，
，18，0.10100100011…（相邻两个 1 之间 0 的个数逐次加 1）中，无理数有（）
4
3
A. 1 个
3. 若 x
B. 2 个
C. 3 个
D. 4 个
y ，则下列不等式一定成立的是（）
A.
x
y
B. 2
x
2
y
C.
x
6
y
6
D.
x
4. 若实数 m，n满足
(
m
12)
2
|
n
15 | 0
，则 n m 的立方根为（）
4
y
4
A. -3
B. 3
C. ±3
5. 下列二次根式中，是最简二次根式的是（）
A.
6
B.
8
C.
1
3
6. 不等式
8
x
3
x
5
10
的解集在数轴上表示为（）
D.
3 3
D.
4
A.
C.
B.
D.
7. 如图，为了求出分别位于池塘两岸的点 A与点 B的距离，小亮在点 C处立一标杆，使 ABC
测得 AC的长为 85m，BC的长为 75m，则点 A与点 B的距离是（）
是直角，
x a 的非负整数解是 0，1，2，则 a应满足的条件是（）
C. 30m
D. 50m
B. 40m
0
A. 20m
8. 若关于 x的不等式5
学科 网（北 京）股 份有限 公司
A.
a
10
B.
a
10
C. 10
a
15
D. 10
a
15
二、选择题（本题共 4 小题，每小题 5 分，共 20 分．在每小题给出的选项中，有多项符合题目要求，全部
选对的得 5 分，有选错的得 0 分，部分选对的得 2 分．）
9. 下列二次根式中，化简后能与 2 合并的是（）
A.
4
B.
8
C.
12
D.
32
10. 下列计算中正确的是（）
A.
C.
18
2
3
24
4
11. 如果不等式组
A.
1
3
B.
4 2
2
8
D. 2 2 2 3
2 6
1
2
x
x
a
的解集是
x ，那么 a的值可能是（）
1
2
B. -1
C. -0.7
D. -2
12. 我国是最早了解勾股定理的国家之一．据《周髀算经》记载，勾股定理的公式与证明是在商代由商高
发现的，故又称之为“商高定理”；三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释，
并给出了另外一个证明，下面四幅图中，能证明勾股定理的是（）
A.
C.
B.
D.
三、填空题（本大题共 4 小题，共 20 分，只要求填写最后结果，每小题填对得 5 分）
第Ⅱ卷（非选择题，98 分）
13. 实数 a，b在数轴上的位置如图所示，化简 2
a
|
b a
________．
|
14. 已知不等式组
1
x a
2
x b
2
的解集为 2
x
，则
3
a b
2022
的值为________．
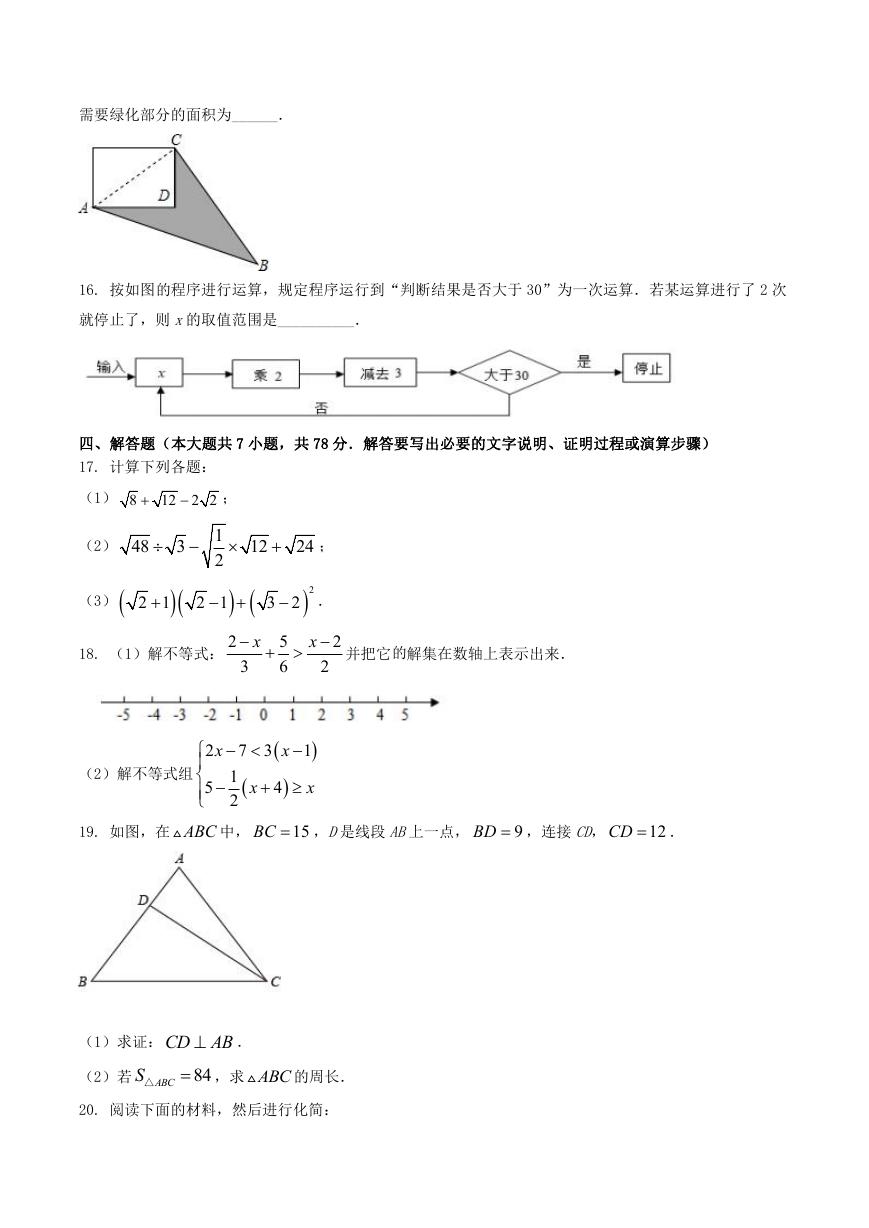
15. 学校操场边上一块空地（阴影部分）需要绿化，测出 CD=6m，AD=8m，BC=24m，AB=26m，AD⊥CD，那么
学科 网（北 京）股 份有限 公司
需要绿化部分的面积为______．
16. 按如图的程序进行运算，规定程序运行到“判断结果是否大于 30”为一次运算．若某运算进行了 2 次
就停止了，则 x的取值范围是__________．
四、解答题（本大题共 7 小题，共 78 分．解答要写出必要的文字说明、证明过程或演算步骤）
17. 计算下列各题：
（1） 8
12
2 2
；
（2）
48
3
1
2
12
24
；
（3）
2 1
18. （1）解不等式：
2 1
2
x
3
3 2
2
．
x
2
5
6
2
并把它的解集在数轴上表示出来．
（2）解不等式组
2
x
15
2
19. 如图，在 ABC
7 3
x
4
x
1
x
中，
BC ，D是线段 AB上一点，
15
BD ，连接 CD，
9
CD ．
12
（1）求证：CD AB ．
（2）若
S
△
ABC
84
，求 ABC
的周长．
20. 阅读下面的材料，然后进行化简：
学科 网（北 京）股 份有限 公司
在进行二次根式的化简与运算时，我们有时会碰上形如 5
3
,
2
3
,
2
3 1
的式子，其实我们还可以将其进一
步化简： 5
3
2
3 1
5
3
3
3
3 1
2
3 1
3 1
5 3
3
2
,
3
2
3
3 1
2
2
1
2 3
3 3
2
6
3
，
3 1
2
3 1
这种化简的过程叫做分母有理化．
（1）
（2）
（3）
；
3
27
2
3 1
1
3 1
；
1
5
3
1
7
1
3
5
．
7
21. 随着 2022 年北京冬奥会的进行，冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”深受广大人民
的喜爱．某网店 2021 年 12 月份上架了“冰墩墩”和“雪容融”，当月售出了 100 个“冰墩墩”和 40 个“雪
容融”，销售总额为 14 800 元．2022 年 1 月售出了 160 个“冰墩墩”和 60 个“雪容融”，销售总额为 23
380 元．
（1）求“冰墩墩”和“雪容融”的销售单价；
（2）店主 2022 年 2 月又购进了 200 个“冰墩墩”和 160 个“雪容融”上架到网店，在“冰墩墩”售出
3
4
，
“雪容融”售出
1
2
后，为了尽快回笼资金，店主决定对剩余的“冰墩墩”每个打 a折销售，对剩余的“雪
容融”每个降价 3a元销售，很快全部售完．若要保证本月销售总额不低于 32500 元，求 a的最小值．
22. （1）观察各式： 0.03
0.1732, 3 1.732, 300 17.32
．．．
发现规律：被开方数的小数点每向右移动_________位，其算术平方根的小数点向______移动______位；
（2）应用：已知 5
2.236
，则 0.05 ________， 500 _________；
（3）拓展：已知 6
2.449, 60
7.746
，计算 240 和 0.54 的值．
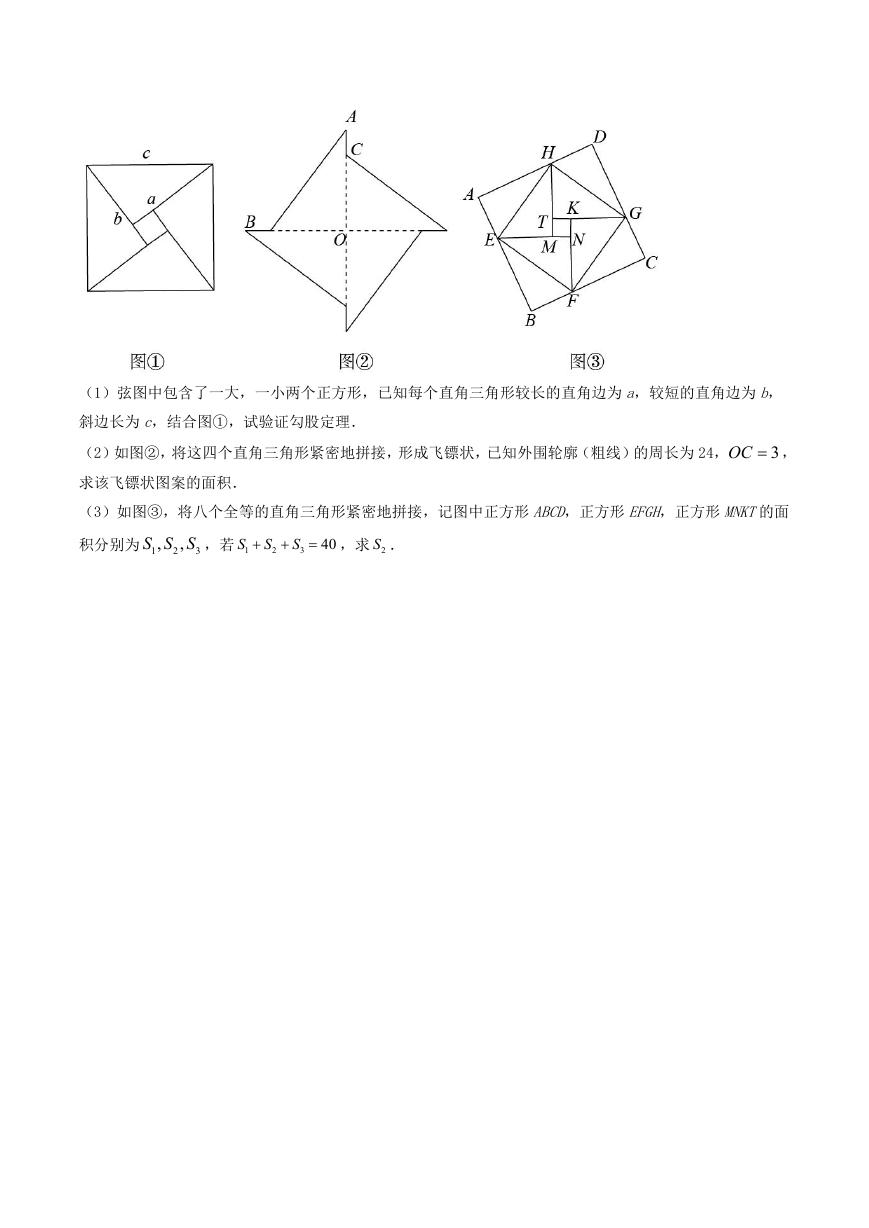
23. 如图①，美丽的弦图，蕴含着四个全等的直角三角形．
学科 网（北 京）股 份有限 公司
（1）弦图中包含了一大，一小两个正方形，已知每个直角三角形较长的直角边为 a，较短的直角边为 b，
斜边长为 c，结合图①，试验证勾股定理．
（2）如图②，将这四个直角三角形紧密地拼接，形成飞镖状，已知外围轮廓（粗线）的周长为 24，
OC ，
3
求该飞镖状图案的面积．
（3）如图③，将八个全等的直角三角形紧密地拼接，记图中正方形 ABCD，正方形 EFGH，正方形 MNKT的面
积分别为 1
,
2
S S S ，若 1
S
,
3
S
2
S
3
，求 2S ．
40
学科 网（北 京）股 份有限 公司
一、选择题（本题共 8 小题，每小题 4 分，共 32 分，在每个小题给出的四个选项中，只有一项是符合题目
参考答案
第Ⅰ卷（选择题，52 分）
要求的）
【1 题答案】
【答案】A
【2 题答案】
【答案】B
【3 题答案】
【答案】D
【4 题答案】
【答案】A
【5 题答案】
【答案】A
【6 题答案】
【答案】C
【7 题答案】
【答案】B
【8 题答案】
【答案】D
二、选择题（本题共 4 小题，每小题 5 分，共 20 分．在每小题给出的选项中，有多项符合题目要求，全部
选对的得 5 分，有选错的得 0 分，部分选对的得 2 分．）
【9 题答案】
【答案】BD
【10 题答案】
【答案】AC
【11 题答案】
【答案】BCD
【12 题答案】
【答案】ABC
三、填空题（本大题共 4 小题，共 20 分，只要求填写最后结果，每小题填对得 5 分）
第Ⅱ卷（非选择题，98 分）
【13 题答案】
【答案】 b
【14 题答案】
学科 网（北 京）股 份有限 公司
【答案】1
【15 题答案】
【答案】96
【16 题答案】
【答案】
39
4
x
33
2
四、解答题（本大题共 7 小题，共 78 分．解答要写出必要的文字说明、证明过程或演算步骤）
【17 题答案】
【答案】（1） 2 3
（2） 4
6
（3）8 4 3
【18 题答案】
【答案】（1） 3x ，见解析；（2） 4
【19 题答案】
x
．
2
【答案】（1）证明见解析.
（2）42
【20 题答案】
【答案】（1） 3
3
（2） 3 1
（3）1
【21 题答案】
【答案】（1）“冰墩墩”的销售单价为 118 元，“雪容融”的销售单价为 75 元
（2）8
【22 题答案】
【答案】（1）2；右；1
（2）0.2236；22.36
（3）15.492，0.7347
【23 题答案】
【答案】（1）见解析
（2）24
（3）
40
3
学科 网（北 京）股 份有限 公司
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
