第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
2022-2023学年安徽省蚌埠市蚌山区八年级下学期期中数学试题及答案.doc
2022-2023 学年安徽省蚌埠市蚌山区八年级下学期期中数学试题及答
注意事项：
1.你拿到的试卷满分为 150 分，考试时间为 120 分钟.
案
2.试卷包括“试题卷”和“答题卷”两部分，“试题卷”共 4 页.“答题卷”共 6 页.
3.请务必在．．．．“答题卷．．．”上答题．．．，在“试题卷”上答题是无效的.
一、选择题（本大题共 10 小题，每小题 4 分，满分 40 分）
1.下列各式中，一定是二次根式的是（ ）
A. a
B.
2 1
a
C. 3 2
D.
2
2.下列各组二次根式中，属于同类二次根式的是（ ）
A. 12 与 18
B. 15 与 2
C. 0.5 与 5
D. 8 与 2
3.用配方法解方程 2 6
x
x
A. 3
B.3
，若配方后结果为
1 0
C. 3
x m
2
，则 m 的值为（ ）
10
D.6
4.若 4 是方程 2
x
6
x
k
的一个根，则方程的另一个根是（ ）
0
A.2
B.3
C.4
D.5
5.下列一元二次方程中，有两个不相等的实数根的是（ ）
A.
23
x
4
x
1 0
1 0
C. 2 2
x
x
6.在平面直角坐标系中，点
P
1,
B.
22
x
x
1 0
D. 2
x
x
1 0
2
到原点的距离为（ ）
A.1
B. 2
C. 3
D.3
7.已知三角形的三边长为 a ，b ， c ，且满足
a b
2
2
c
2
ab
，则这个三角形的形状是（ ）
A.等边三角形
B.钝角三角形
C.锐角三角形
D.直角三角形
8.《九章算术》是我国传统数学中重要的著作之一，奠定了我国传统数学的基本框架.其中，方程术是《九
章算术》最高的数学成就.《九章算术》记载：“今有户高多于广六尺八寸，两隅相去适一丈.问户高、广
各几何？”大意：有一扇形状是长方形的门，它的高比宽多 6 尺 8 寸，它的对角线长 1 丈，问它的高与宽
各是多少？利用方程思想设长方形门宽为 x 尺，则依题意所列方程为（ ）（注：1 丈 10 尺，1 尺 10 寸）
A.
2
x
x
6.8
2
2
10
C.
x
6.8
2
2
x
2
10
B.
2
x
x
6.8
2
2
100
D. 2
x
2
6.8
2
100
学科 网（北 京）股 份有限 公司
9.如图，在 ABC△
的任意一点，则 PA PC 的最小值为（ ）
BAC
，
中，
90
AC ，
6
BC ，MN 是线段 BC 的中垂线，P 是直线 MN 上
10
B.7
A.6
10.在 Rt ABC△
一点，且 FB BC
C.8
D.10
90
， D ， E 为 BC 上两点，
BAC
DAE
45
， F 为 ABC△
外
中， AB AC
， FA AE
，
，则下列结论中错误的是（ ）
A.CE BF
1
2
ADE
C.
S
△
B.
2
BD CE
2
2
DE
AD EF
D.
2
CE
2
BE
2
AE
2
二、填空题（本大题共 4 小题，每小题 5 分，满分 20 分）
11.化简：
______.
3 π
2
x
0
x m
没有实数根，则 m 的取值范围是______.
12.方程 2 2
13.如图，在 4 4 的正方形网格中，每个小正方形的边长均为 1，点 A ，B ，C 都在格点上，BD AC
点 D ，则 BD 的长为______.
于
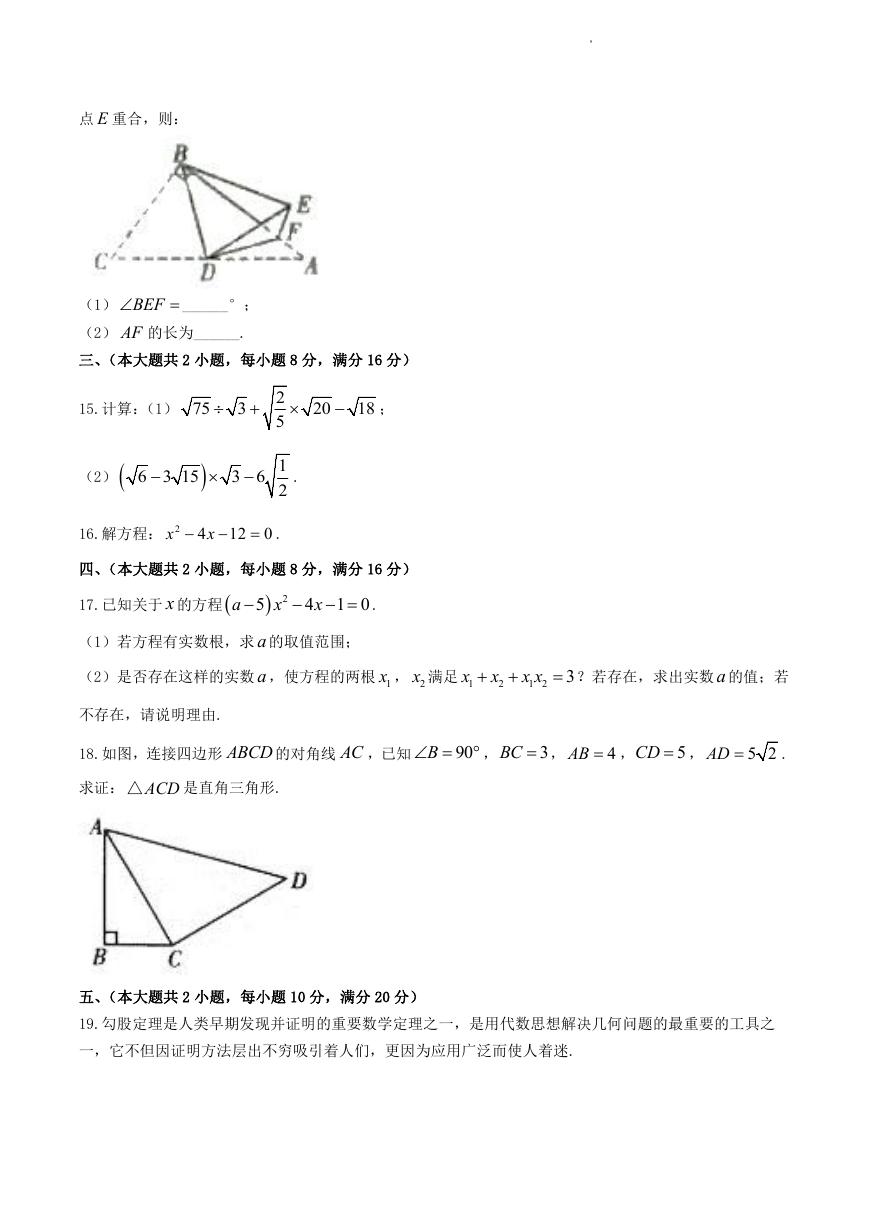
14 如图，在 ABC△
沿 BD 翻折，使C 落在点 E 处，点 F 为直角边 AB 上一点，连接 DF ，将 ADF△
BC ，点 D 为斜边 AC 的中点，连接 BD ，将 BCD△
沿 DF 翻折，使点 A 与
AC ，
ABC
，
中，
90
5
3
学科 网（北 京）股 份有限 公司
点 E 重合，则：
（1） BEF
______°；
（2） AF 的长为______.
三、（本大题共 2 小题，每小题 8 分，满分 16 分）
15.计算：（1）
75
3
（2）
6 3 15
3 6
2
5
1
2
16.解方程： 2
x
4
x
12
0
.
20
18
；
.
四、（本大题共 2 小题，每小题 8 分，满分 16 分）
17.已知关于 x 的方程
（1）若方程有实数根，求 a 的取值范围；
（2）是否存在这样的实数 a ，使方程的两根 1x ， 2x 满足 1
x
1 0
.
25
x
a
4
x
x
2
x x
1 2
？若存在，求出实数 a 的值；若
3
不存在，请说明理由.
18.如图，连接四边形 ABCD 的对角线 AC ，已知
求证： ACD△
是直角三角形.
B
90
，
BC ，
3
AB ，
4
CD ，
5
AD
5 2
.
五、（本大题共 2 小题，每小题 10 分，满分 20 分）
19.勾股定理是人类早期发现并证明的重要数学定理之一，是用代数思想解决几何问题的最重要的工具之
一，它不但因证明方法层出不穷吸引着人们，更因为应用广泛而使人着迷.
学科 网（北 京）股 份有限 公司
（1）应用场景 1—在数轴上画出表示无理数的点.如图 1，在数轴上找出表示 3 的点 A ，过点 A 作直线l 垂
直于OA ，在l 上取点 B ，使
AB .以原点O 为圆心，OB 为半径作弧，则弧与数轴的交点C 表示的数
是______；
（2）应用场景 2——解决实际问题.如图 2，秋千由静止铅锤位置 AB 推至 AC 处，它的绳索始终拉直，量
得水平距离
DB ，求绳索 AC 的长.
1m
2
CD ，
2m
20.一商店销售某种商品，平均每天可售出 20 件，每件盈利 40 元.为了扩大销售，增加盈利，对该商品采
取了降价措施，在每件盈利不少于 25 元的前提下，经过一段时间的销售发现，如果这种商品的售价每降低
1 元，那么平均每天可多售出 2 件.
（1）若这种商品降价 x 元，则它平均每天的销售数量为多少件？（用含 x 的代数式表示）
（2）当这种商品每件降价多少元时，它平均每天的销售利润为 1200 元？
六、（本题满分 12 分）
21.光明中学准备在校园里利用围墙（墙长15m ）和 42m 长的篱笆墙围建劳动实践基地.该校某数学兴趣小
组设计了如下的围建方案（除围墙外，实线部分均为篱笆墙，且不浪费篱笆墙）：利用围墙和篦笆围成Ⅰ，
Ⅱ两块长方形劳动实践基地，且在Ⅱ区中留一个宽度
EH 的长方形水池.已知
1m
OG
2
DG
，劳动基地
的总面积（不包含水池）为
100m ，求 DG 的长是多少？
2
七、（本题满分 12 分）
22.课堂上学习了勾股定理后，知道“勾三、股四、弦五”.老师给出一组数让学生观察：3，4，5；5，12，
13；7，24，25；9，40，41；…，学生发现这些勾股数的勾都是奇数，且从 3 起就没有间断过，于是老师
提出以下问题让学生解决.
（1）请你根据上述的规律写出下一组勾股数：11，______，______；
（2）若第一个数用字母 a（ a 为奇数，且 3a ）表示，那么后两个数用含 a 的代数式分别怎么表示？聪明
的小明发现每组第二个数有这样的规律：
4
23
1
2
，
12
25
1
2
，
24
1
27
2
，…，则用含 a 的代数式表
学科 网（北 京）股 份有限 公司
示每组第二个数和第三个数分别为______，______；
（3）用所学知识证明（2）中你所发现的这类用字母 a 表示的勾股数的规律.
八、（本题满分 14 分）
23.王昊是同学在一次课外活动中，用硬纸片做了两个直角三角形，见图 1、图 2.
90
30
，
，
BC
A
B
5cm
图 1 中，
图 3 是王昊同学所做的一个实验：他将 DEF△
DEF△
（1）在将 DEF△
变”“变大”或“变小”）
沿 AC 方向移动.在移动过程中， D ， E 两点始终在 AC 边上（移动开始时点 D 与点 A 重合）.
沿 AC 方向移动的过程中，王昊同学发现： F ，C 两点间的距离逐渐______；（填“不
D
，
；图 2 中，
的直角边 DE 与 ABC△
90
45
，
E
的斜边 AC 重合在一起，并将
DE
3cm
.
（2）王昊同学经过进一步研究，编制了如下问题：
问题①：当 DEF△
问题②：当 DEF△
角形是直角三角形？
移动至什么位置，即 AD 的长为多少时， F ，C 的连线与 AB 平行？
移动至什么位置，即 AD 的长为多少时，以线段 AD ，FC ，BC 的长度为三边长的三
请你分别完成上述两个问题的解答过程.
学科 网（北 京）股 份有限 公司
参考答案
一、选择题（本大题共 10 小题，每小题 4 分，满分 40 分）
1. B
2. D
3. B
4. A
5. A
6. C
7. D
8. A
9. C
10. C
二、填空题（本大题共 4 小题，每小题 5 分，满分 20 分）
11. π 3
12.
1m
13. 9
5
14.（1）90 （2） 7
8
三、（本大题共 2 小题，每小题 8 分，满分 16 分）
15.解：（1）
75
3
2
5
20
18 5 3
3
2
5
2 5 3 2
5 2 2 3 2
；………………（4 分）
5
2
（2）
6 3 15
3 6
1
2
6
3 3 15
3 6
1
2
18 3 45 6
2
2
3 2 9 5 3 2
9 5
.………………（8 分）
16.解： 2
x
4
x
12
，分解因式，得
0
x
6
x
2
，
0
x 或 2 0
x ，
6 0
解得 1
x ， 2
6
x .………………（8 分）
2
四、（本大题共 2 小题，每小题 8 分，满分 16 分）
17.解：（1）当 5a 时，方程为 4
x
Δ 16 4
4 0
5
4
a
1 0
，方程有实数根；当 5a 时，方程为一元二次方程，
a
，解得 1a ， a 的取值范围为 1a ；………………（4 分）
x
（2）存在.根据题意，可得 1
x
2
3
，解得 6a .
4
5
a
1
5
a
4
5
a
x x
， 1 2
1
5
a
x
， 1
x
2
x x
1 2
3
，
经检验， 6a 是方程的解.………………（8 分）
18.证明：
B
90
，
BC ，
3
AB ，
4
AC
2
BC
2
AB
2
3
2
4
.……（3 分）
5
， 2
AD ，
50
50
AC
2
CD
2
2
AD
.
5
AC
ACD
△
，
CD ，
5
AD
5 2
，
2
AC
CD
2
是直角三角形.………………（8 分）
学科 网（北 京）股 份有限 公司
五、（本大题共 2 小题，每小题 10 分，满分 20 分）
19.解：（1）在 Rt OAB△
中，
OB
2
OA
2
AB
2
3
2
2
13
，
OC
13
，
点C 表示的数是 13 ，故答案为 13 ；………………（4 分）
（2）设秋千绳索 AC 的长度为 mx ，由题意可得
m
AD AB BD x
AC AB x
1 m
，
，
CD
2m
，
BD ，
1m
2
2
AC
，
中， 2
AD DC
在 Rt ADC△
2
1
答：绳索 AC 的长为 2.5m .………………（10 分）
20.解：（1）若设每件商品降价 x 元，
则平均每天的销售数量为
20 2x
x
件；………………（3 分）
2
2
2
，解得 2.5
x ，即 AC 的长度为 2.5m .
x
（2）设每件商品降价 x 元，则每件盈利
40 x 元，平均每天销售数量为
20 2x
件，
x
40
20 2
依题意得，
又 40
x
当每件商品降价 10 元时，该商店平均每天的销售利润为 1200 元.………………（10 分）
x ，
，解得 1 10
，整理，得 2
x
x ， 2
x
1200
x
200
10
15
25
30
，
0
x
x
.
20
.
六、（本题满分 12 分）
21 解：设 DG 的长为 mx ，则CG 的长为 2 mx ，
HG AD
42
2
x
x
3
14
x
m
，
EG HG
1
14
x
1
13
x
m
.
14
x
2 13
x
x
100
，………………（6 分）
x ， 2 10
x
.………………（10 分）
由题意得
x
10
3
15
解得 1
DC
DC
3
，
DG
答： DG 的长是 10 m
3
，即
DG ，
5
DG
10
不符合题意，舍去.
.………………（12 分）
七、（本题满分 12 分）
22.解：（1）由题意可得，第二个数是第一个数的平方与 1 的差除以 2，第三个数是第一个数的平方与 1 的
和除以 2， 第二个数是
1 60
，第三个数是
211
2
1 61
211
2
.故答案为 60，61；………………（4 分）
（2）由题意可得，第二个数是第一个数的平方与 1 的差除以 2，第三个数是第一个数的平方与 1 的和除以
2， 第二个数是
2 1
a
2
，第三个数是
2 1
a
2
.故答案为
2 1
a
2
，
2 1
a
2
；………………（8 分）
学科 网（北 京）股 份有限 公司
（3）证明：由题意可得，
1
a
2
2
2
1
a
2
2
2
a
2
2
1
1
a
2
2
a
2
2
1
1
a
2
2
a
2
1
2
a
，
勾股数的规律是 a ，
2 1
a
2
，
2 1
a
2
.………………（12 分）
八、（本题满分 14 分）
23.解：（1）在将 DEF△
案为变小；………………（2 分）
沿 AC 方向移动的过程中，观察图象可知， F ，C 两点间的距离逐渐变小.故答
（2）①如图.
AC
3cm
，
BC
2
DF
10cm
3cm
.
.
30
5cm
BC
，
，
45
DEF
DE
，
30
FCD
A
3 3cm
DC
90
B
A
，
90
FDE
，
当 FC AB∥ 时，
在 Rt FDC△
10 3 3 cm
AD x
，在 Rt FDC△
AD
当
cm
②设
中，
，
.
时， FC AB∥ ；
AD AC DC
10 3 3 cm
，
（6 分）
中，
2
FC
2
DC
2
FD
10
2
x
，
9
21
5
67
10
（Ⅰ）当 FC 为斜边时，由 2
AD BC
2
2
FC
，得
2
x
25
10
2
x
，解得
9
（Ⅱ）当 AD 为斜边时，由 2
FC
2
BC
2
AD
，得
10
x
2
9 5
2
2
，解得
x
x ；
x ；
（Ⅲ）当 BC 为斜边时，由 2
AD FC
2
2
BC
，得
2
x
10
x
2
，整理得 2 10
25
9
x
x
42
，
0
Δ 100 168
由（Ⅰ）、（Ⅱ）、（Ⅲ）得，当
68 0
， 方程无解，
21cm
5
AD
或 67 cm
10
时，以线段 AD ， FC ， BC 的长度为三边长的三
角形是直角三角形. …………（14 分）
学科 网（北 京）股 份有限 公司
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
