logo资料库

2022-2023学年山东省滨州市阳信县八年级下学期期中数学试题及答案.doc

发布时间：2023-10-13 发布人：admin 分类：说明书 资料大小：3.04M 资料格式：doc 举报 版权申诉
第1页 / 共12页
第2页 / 共12页
第3页 / 共12页
第4页 / 共12页
第5页 / 共12页
第6页 / 共12页
第7页 / 共12页
第8页 / 共12页
资料共12页，剩余部分请下载后查看
    2022-2023 学年山东省滨州市阳信县八年级下学期期中数学试题及答 案 温馨提示： 1．本试卷分第Ⅰ卷和第Ⅱ卷两部分，共 8 页。满分为 120 分。考试用时 120 分钟。考试结束后，只上交答 题卡。 2．答卷前，考生务必用 0.5 毫米黑色签字笔将自己的学校、班级、姓名、准考证号、考场填写在答题卡规 定的位置上，并用 2B 铅笔填涂相应位置。 3．第Ⅰ卷每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净 后，再选涂其他答案标号。答案不能答在试题卷上。 4．第Ⅱ卷必须用 0.5 毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在 试题卷上；不准使用涂改液、胶带纸、修正带。不按以上要求作答的答案无效。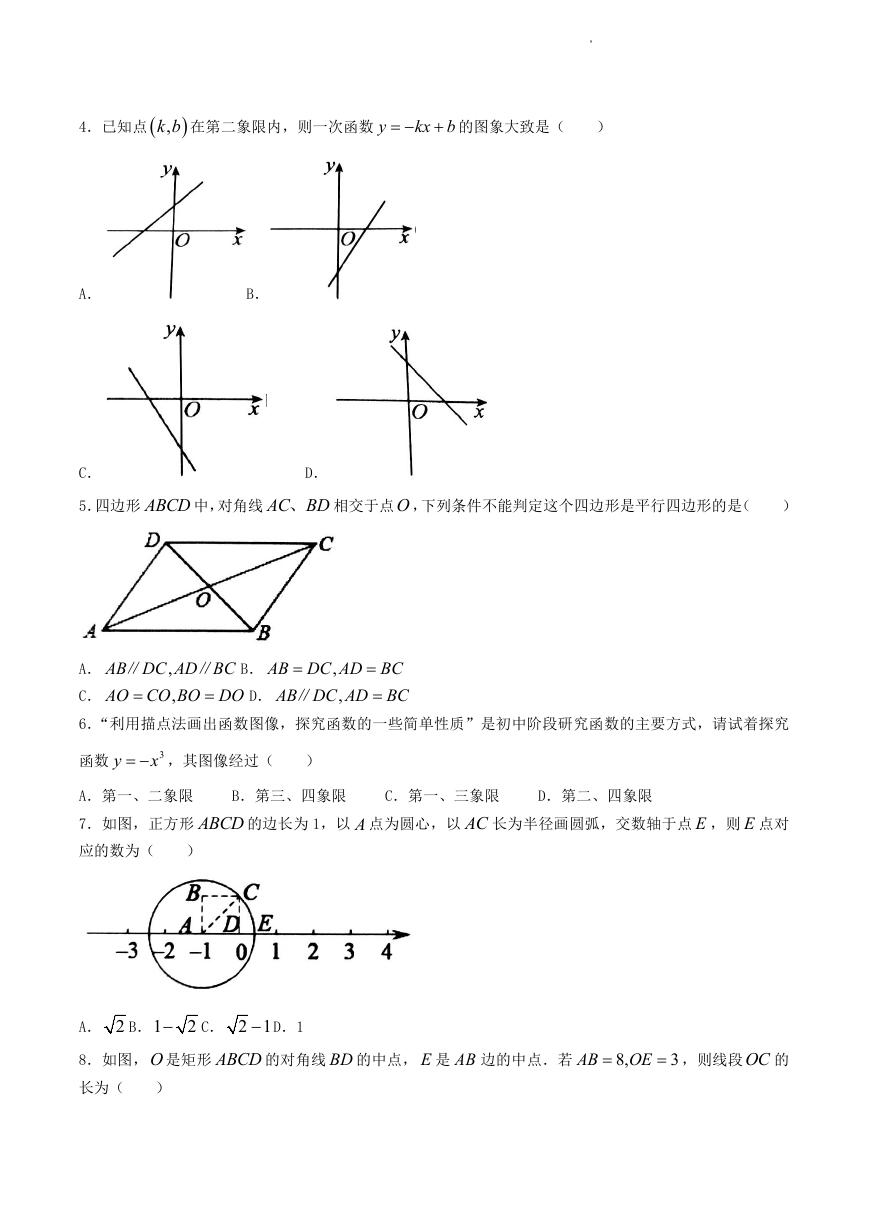 第Ⅰ卷（选择题） 一、选择题：本大题共 12 个小题，在每个小题的四个选项中只有一个是正确的，请把正确的选项选出来， 用 2B 铅笔把答题卡上对应题目的答案标号涂黑，每小题涂对得 3 分，满分 36 分． 1．函数 y  x  3 x 中，自变量 x 的取值范围是（ ） A． 3x  B． 3x  C． 3x  D． 3x  2．下列图象中， y 不是 x 的函数的是（ ） A． B． C． D． 3．若一次函数  y m   3 x  的图象经过点  4 1,A x y 和点   1 B x y ，当 1 x , 2 2  x 时， 1 y 2 y ，则 m 的 2 取值范围是（ 3m  B． A． ） 3m  C． 3m  D． 3m  学科 网（北 京）股 份有限 公司
    4．已知点 ,k b 在第二象限内，则一次函数 y   kx b  的图象大致是（ ） A． B． C． D． 5．四边形 ABCD 中，对角线 AC BD、 相交于点O ，下列条件不能判定这个四边形是平行四边形的是（ ） A． C． AB DC AD BC AO CO BO DO ∥ B．  ∥  , , D． , AB DC AD BC AB DC AD BC  ∥  , 6．“利用描点法画出函数图像，探究函数的一些简单性质”是初中阶段研究函数的主要方式，请试着探究 函数 y x  ，其图像经过（ 3 ） B．第三、四象限 A．第一、二象限 7．如图，正方形 ABCD 的边长为 1，以 A 点为圆心，以 AC 长为半径画圆弧，交数轴于点 E ，则 E 点对 应的数为（ C．第一、三象限 D．第二、四象限 ） 2 C． 2 1 D．1 A． 2 B．1 8．如图，O 是矩形 ABCD 的对角线 BD 的中点， E 是 AB 边的中点．若 长为（ ） AB  8, OE  ，则线段OC 的 3 学科 网（北 京）股 份有限 公司
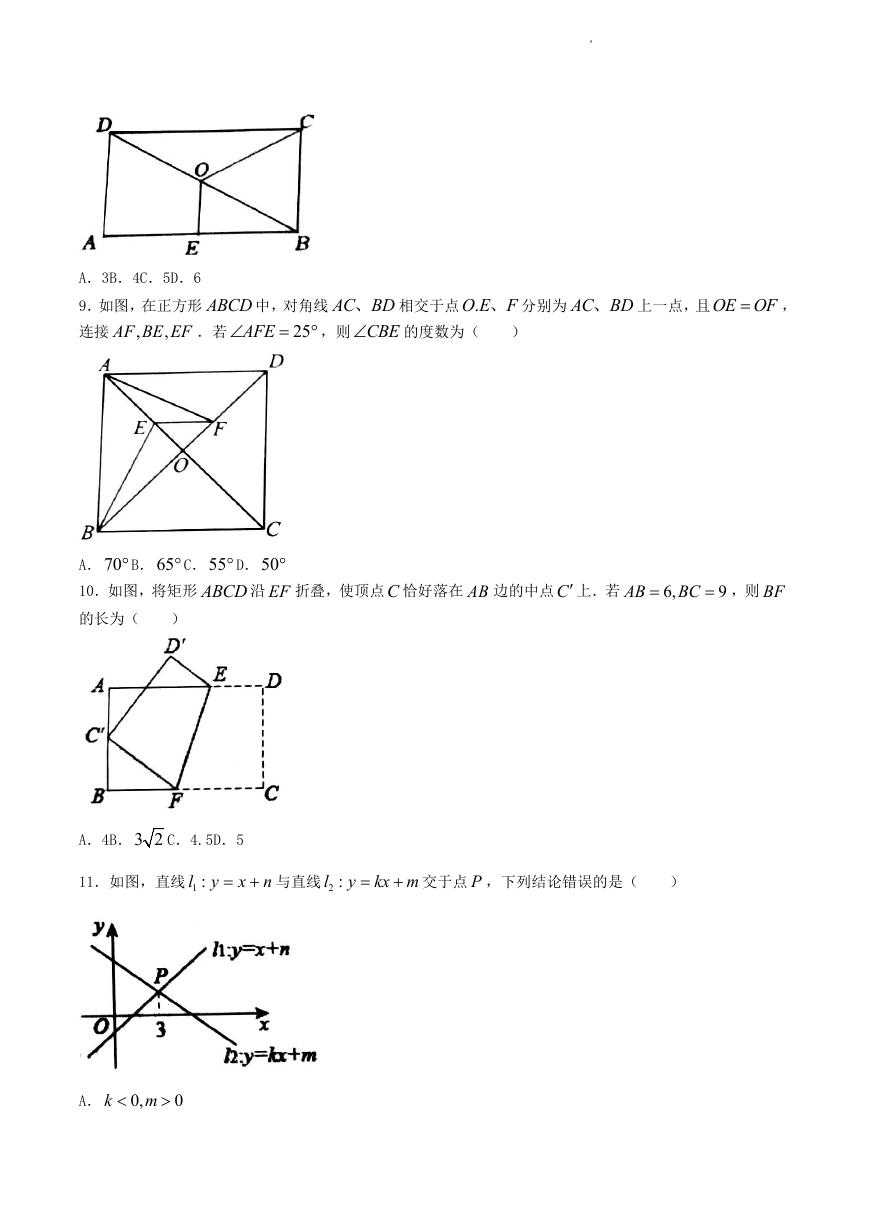
    A．3B．4C．5D．6 9．如图，在正方形 ABCD 中，对角线 AC BD、 相交于点 .O E F、 分别为 AC BD、 上一点，且OE OF 连接 , AF BE EF ．若  ，则 CBE 的度数为（ AFE ） ,  25 ， A．70 B．65 C．55 D．50 10．如图，将矩形 ABCD 沿 EF 折叠，使顶点C 恰好落在 AB 边的中点C 上．若 的长为（ ） AB  6, BC  ，则 BF 9 A．4B．3 2 C．4.5D．5 11．如图，直线 1 :l y   与直线 2 : x n l y  kx m  交于点 P ，下列结论错误的是（ ） A． 0, m k  0 学科 网（北 京）股 份有限 公司
    B．关于 x的方程 x n kx m C．关于 x的不等式   1k   的解为 3x    的解集为 3x  n m x D．直线 1l 上有两点 , x y 1 1   , x y ，若 1 x 2 , 2  x 时，则 1 y 2 y 2 12．动物园内的一段路线如图 1 所示，园内有免费的班车，从入口处出发，沿该线路开往熊猫馆，途中停 靠海洋馆（上下车时间忽略不计），第一班车上午 9：00 发车，以后每隔 10 分钟有一班车从入口处发车， 且每一班车速度均相同，小明周末到动物园游玩，上午 8：35 到达入口处，因还没到班车发车时间，于是 从入口处出发，沿该线路步行 30 分钟后到达海洋馆、离入口处的路程 y（米）与时间 x（分）的函数关系 如图 2 所示，下列结论正确的是（ ） A．第一班车从入口处到达熊猫馆所需的时间为 15 分钟 B．第一班车离入口处的路程 y （米）与时间 x （分）的关系式为 y  200 x  4000 25    x 45  C．第一班车到达海洋馆时小明已经在海洋馆停留了 10 分钟 D．小明在海洋馆游玩 35 分钟后，想坐班车到熊猫馆，则小明最早能够坐上第四班车 第Ⅱ卷（非选择题） 二、填空题：本大题共 6 个小题，每小题 4 分，满分 24 分．只要求填写最后结果． 13．已知函数    是关于 x 的一次函数，则 m  __________． 2 3 m x  m 2 6 y   14．若一次函数 y 2 x  的图象向上平移 m 个单位后，所得图象经过点 1 1,0 ，则 m  __________． 15．在一次函数 3 x y  的图象上，到 y 轴的距离等于 2 的点的坐标是__________． 2 16．如图，在菱形 ABCD 中，对角线 ,AC BD 相交于点 , 则 EF 的长为__________． O BD  6, AC  ，直线OE AB 交CD 于点 F ， 8 学科 网（北 京）股 份有限 公司
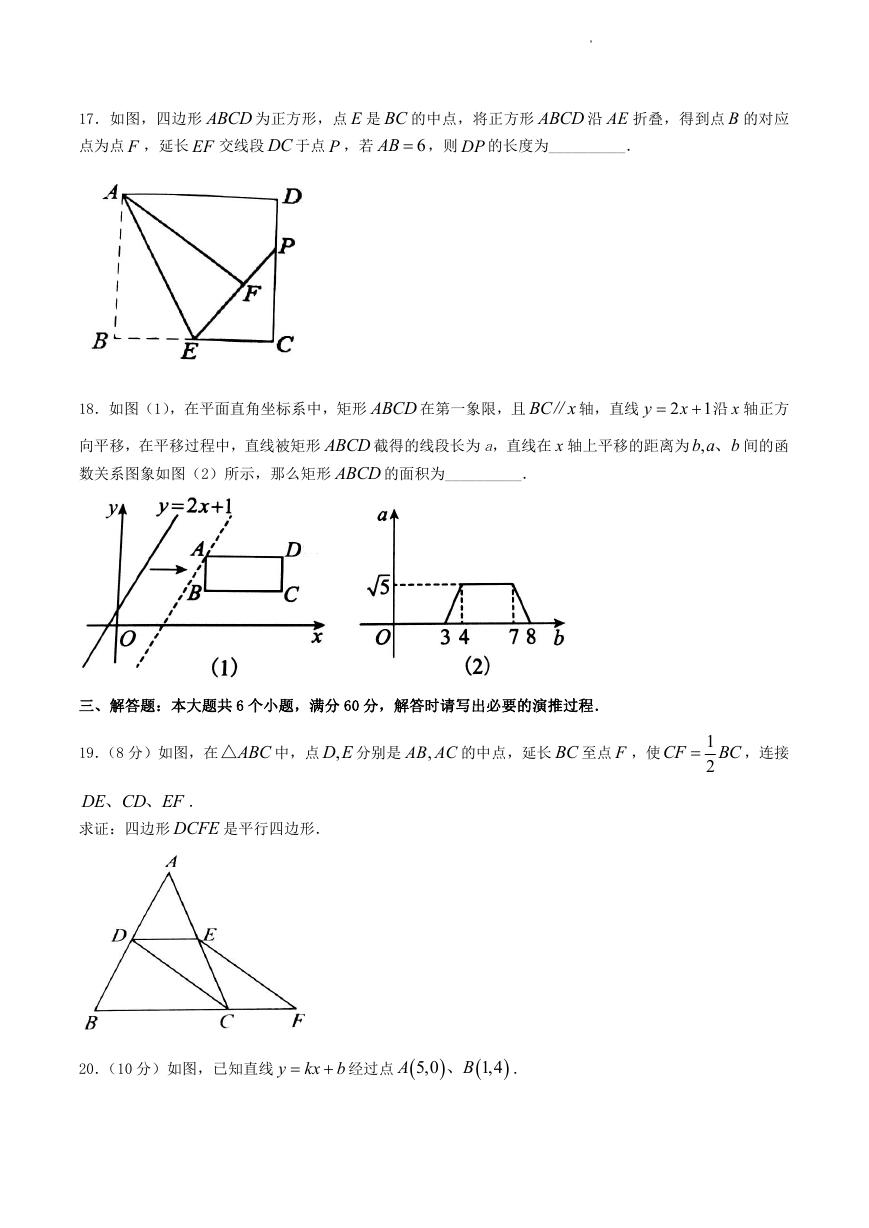
    17．如图，四边形 ABCD 为正方形，点 E 是 BC 的中点，将正方形 ABCD 沿 AE 折叠，得到点 B 的对应 点为点 F ，延长 EF 交线段 DC 于点 P ，若 AB  ，则 DP 的长度为__________． 6 18．如图（1），在平面直角坐标系中，矩形 ABCD 在第一象限，且 BC x∥ 轴，直线 y 2 x 1  沿 x 轴正方 向平移，在平移过程中，直线被矩形 ABCD 截得的线段长为 a，直线在 x 轴上平移的距离为 ,b a b、 间的函 数关系图象如图（2）所示，那么矩形 ABCD 的面积为__________． 三、解答题：本大题共 6 个小题，满分 60 分，解答时请写出必要的演推过程． 19．（8 分）如图，在 ABC△ 中，点 ,D E 分别是 ,AB AC 的中点，延长 BC 至点 F ，使 CF  1 2 BC ，连接 、 、 ． DE CD EF 求证：四边形 DCFE 是平行四边形． 20．（10 分）如图，已知直线 y  kx b  经过点  A 5,0  B、  1,4  ． 学科 网（北 京）股 份有限 公司
    （1）求直线 AB 的解析式； （2）若直线 y 2 x  与直线 AB 相交于点C ，请问直线 4 y   2 3 x  是否也经过点 C ？ 4 21．（10 分）如图，在平行四边形 ABCD 中，O 为 BD 的中点，过点O 作 EF 于点 F ． BD 交 AD 于点 E ，交 BC （1）求证：四边形 BEDF 是菱形； （2）若   BAD 2, AD AB  4,  120  ，求 DE 的长． 22．（10 分）为深人学习党的二十大精神，某校举办了“学习二十大，奋进新征程”知识竞赛，学校计划购 买两种奖品共计 30 份分别发放给获得一等奖、二等奖的同学，获奖同学各发一份奖品，同一等级奖品相同， 设一等奖奖品的单价为 x元，购买两种奖品的总费用为 y元． （1）若购买一等奖、二等奖奖品的单价分别为 40 元、20 元，则学校共需花费 800 元，求获得一等奖、二 等奖的人数分别是多少？ （2）在（1）的结果下，若一等奖、二等奖奖品的单价的和为 60 元，一等奖奖品的单价不超过二等奖奖品 单价的 1.5 倍，求总费用 y 的最小值． 23．（10 分）如图，平面直角坐标系 xOy 中，过点 A   0,  1 2    的直线 1l 与直线 2 : l y 2   x  相交于点 4  P m  ，直线 2l 与 x 轴相交于点 B ． , 2  学科 网（北 京）股 份有限 公司
    的面积． （1）求直线 1l 的函数表达式； （2）连接 AB ，求 ABP△ 24．（12 分）【思考研究】 “如图 1，在正方形 ABCD 中，E 是对角线 AC 上一点，点 F 在 DC 的延长线上，且 DE EF 于点G ，求证： BE EF ，”小贤在研究这个问题时，写出了如下的分析过程：先证 ADE 得到 DE BE ，再由 DE EF ，得到 BE EF ，EF 交 BC ABE ， △ ≌△ ． ． （1）请根据小贤的分析过程证明 BE EF 【解决问题】 （2）求 BEF 【拓展延伸】 （3）如图 2，把正方形 ABCD 改为菱形 ABCD ，其他条件不变，当 线段 DE 与线段 BF 的数量关系，并说明理由． 的度数． ABC  60  时，连接 BF ，试探究 一、选择题：本大题共 12 小题，每题 3 分，共 36 分.在每小题给出的四个选项中，只有一项是正确的，请 把正确的选项选出来． 八年级数学答案 学科 网（北 京）股 份有限 公司
    1 D 2 B 3 B 4 A 5 D 6 D 7 C 8 C 9 B 10 A 11 C 12 D 二、填空题：本大题共 6 小题，共 24 分，只要求填写最后结果，每小题填对得 4 分． 13.-2 14. 1 15.（2，4）或（-2，-8） 16. 24 5 （或 4.8） 17. 2 18. 8 三、解答题：本大题共 6 个小题，共 60 分，解答时请写出必要的演推过程． 19.（8 分） 证明：∵在 ABC 中，点 D ， E 分别是边 AB ， AC 的中点， ∴ DE 是 ABC 的中位线，-------------------------------------------1 分 ∴ DE  ∵ CF  1 2 1 2 BC ， DE BC∥ ， ------------------------ ------------------3 分 BC ， B ，C ， F 共线， ∴CF DE ，CF DE∥ ．------------------------ ------------------7 分 故四边形 DCFE 是平行四边形．------------------------ ------------------8 分 20.（10 分） （1）将点 A(5,0)、B(1,4)代入 y=kx+b中， 得：  5 0 k b      4 , k b  ------------------------ ------------------2 分 解得： 1 k      ， 5 b ------------------------ ------------------4 分 ∴直线 AB的解析式为 y=−x+5------------------------ ------------------5 分 2  y x       y x  4 5 ， （2）联立两直线解析式得： 解得： x    y 3 2 ， ∴点 C(3，2)------------------------ ------------------7 分  2 3 4 2 y      3 ------------------------ ------------------9 分 ∴直线 y   2 3 x 21.（10 分）  也经过点 C------------------------ ------------------10 分 4 （1）∵四边形 ABCD 为平行四边形， 学科 网（北 京）股 份有限 公司
    分享到：
    赞 收藏

    相关推荐

    资料库

    初中二年级

    共收录369份资料，累计95个分类，关注成员有19位，主要包括：2021年,2020年,黑龙江,2022年,贵州,内蒙古,云南,青海,吉林,上海,甘肃,浙江,海南,四川,湖南,广西,山西,山东,辽宁,福建,湖北,河南,河北,江西,广东,安徽,天津,陕西,北京,2019年,江苏

    热门标签

    2021年 2020年 黑龙江 2022年 贵州 内蒙古 云南 青海 吉林 上海 甘肃 浙江 海南 四川 湖南 广西 山西 山东 辽宁 福建 湖北 河南 河北 江西 广东 安徽 天津 陕西 北京 2019年 江苏

    最新资料