logo资料库

2021-2022学年北京市海淀区七年级下册期中数学试卷及答案.doc

发布时间：2023-10-12 发布人：admin 分类：说明书 资料大小：0.95M 资料格式：doc 举报 版权申诉
第1页 / 共13页
第2页 / 共13页
第3页 / 共13页
第4页 / 共13页
第5页 / 共13页
第6页 / 共13页
第7页 / 共13页
第8页 / 共13页
资料共13页，剩余部分请下载后查看
    2021-2022 学年北京市海淀区七年级下册期中数学试卷及答 案 一、选择题（本题共 16 分，每小题 2 分） 第 1-8 题均有四个选项，符合题意的只有一个. 1．9 的算术平方根是 A．81B．3 C．±3 D． 3 2．在平面直角坐标系中，点 P（2，3）在 A．第一象限 B．第二象限 C．第三象限 D．第四象限 ，0.1010010001（相邻两个 1 之间依次多一个 0），  2 ， 3 5 ， 4 3. 下列实数 2 ， 1 3 中，无理数有 A．1 个 B．2 个 C．3 个 D．4 个 4．如图，直线 a，b 被 c 所截，则∠1 与∠2 是 A．同位角 B．内错角 C．同旁内角 D．邻补角 5. 下列各数中一定有平方根的是 D． 2 1m  A． 2 1m  B． m C． 1m 6. 一把直尺和一个含30 , 60 角的三角板如图所示摆放，直尺一边 与三角板的两直角边分别交于 F ， A两点，另一边与三角板的两直 角边分别交于 D , E 两点，且 A．10 C．30 7.如图，直线 AB，CD 相交于点 O，分别作∠AOD，∠BOD 的平分线 OE， B． 20 D． 40  ，那么 BAF CED =50 的大小为 OF. 将直线 CD 绕点 O 旋转，下列数据与∠BOD 大小变化无关的是 A. ∠AOD 的度数 B. ∠AOC 的度数 C. ∠EOF 的度数 D. ∠DOF 的度数 8.如示意图，小宇利用两个面积为 1 dm2 的正方形拼成了一个面积为 2 dm2 的大正方形，并 通过测量大正方形的边长感受了 2 dm 的大小. 为了感知更多无理数的大小，小宇利用类 似拼正方形的方法进行了很多尝试，下列做法不能实现的是
    A.利用两个边长为 2dm 的正方形感知 8 dm 的大小 B.利用四个直角边为 3dm 的等腰直角三角形感知 18 dm 的大小 C.利用一个边长为 2 dm 的正方形以及一个直角边为 2dm 的等腰直角三角形感知 6 dm 的 大小 D.利用四个直角边分别为 1 dm 和 3 dm 的直角三角形以及一个边长为 2 dm 的正方形感知 10 dm 的大小 二、填空题（本题共 16 分，每小题 2 分） 9. 如图，要在河岸 l 上建一个水泵房 D ，修建引水渠到村庄C 处．施 工人员的做法是：过点C 作CD l 于点 D ，将水泵房建在了 D 处．这 样修建引水渠 CD 最短，既省人力又省物力，这样做蕴含的数学原理 是 10. 如 图 ， 直 线 a ， b 交 于 点 O ， 若 1 1 = 11. 如图，在四边形 ABCD 中,点 E 在 AD 的延长线上，连接 BD ，如果 添加一个条件，使 AD ∥ BC ，那么可添加的条件为 ． 2 76  ， 则     °． 写出一个即可 ． 12. 在平面直角坐标系中，A 点的坐标为（ 2 ， 1 ），若线段 AB ∥ x 轴， 且 AB  ,则点 B 的坐标为 . 3 13. 用一个实数 a 的值说明命题“ 2a =a ”是假命题，这个 a 的值可以 是__________. 14．为纪念戍边英雄，某班设计了《致敬英雄》主题宣传板报，黑板是 一块长为 2 a 米，宽为 a 米的长方形 ABCD ，版面设计如图所示，将它 分割成两块边长均为 a 米的正方形 ABFE 和正方形 EFCD ，分别以点 ,F B 为圆心，正方形边长为半径画弧.阴影部分用图画展示英雄形象，空白部分用文字宣传 英雄事迹.阴影部分的面积为________平方米（用含 a 的代数式表示）. 15.为迎接校庆，某学校在东西走向的勤学路上修建了一排边长为 1m 的小正方形花坛，如图 1 所示. 小欢和小乐来到花坛边欣赏风景，小欢以自己所在的 A 点为原点，以向东的方向为 正方向，以花坛对角线的长度 2 m 为单位长度建立数轴，如图 2 所示.若小乐在小欢的东 15 m 处，那么在图 2 的数轴上，小乐所在的点位于两个相邻整数之间，这两个整数分别是. 图 1 图 2 16.在平面直角坐标系中，我们定义，点 P 沿着水平或竖直方
    向运动到达点 Q 的最短路径的长度为 P，Q 两点之间的“横纵距离”.如图所示，点 A 的坐标 为（ 2 ,3 ），则 A，O 两点之间的“横纵距离”为 5. （1）若点 B 的坐标为（ -3 -1， ），则 A，B 两点之间的“横纵距离”为； （2）已知点 C 的坐标为（0，2），D，O 两点之间的“横纵距离”为 5，D，C 两点之间的“横 纵距离”为 3.请写出两个满足条件的点 D 的坐标：___________, ____________. 三、解答题（本题共 68 分，第 17，18，20，21，22，25 题，每小题 5 分，第 19,23,24,26 题，每小题 6 分，第 27，28 题，每小题 7 分） 17．计算： 16 - 3 27 解： 3 +（ ） （- ） + . 1 3 2 3 1 18．计算： ( 3 ) 3 1 - + 2 - 3 . 解： 19.求出下列等式中 x 的值： （1） 27 x  ； 63 解： 解： （2） 3 x   . 5 1 2 20．已知：如图，直线 AB ，CD 相交于点O， 的度数. AOC  40  ，OE 平分 BOC ，求 DOE  21．完成下面的证明： 已知：如图， AEC 求证： AB ∥CD . 证明：过点 E 作 EF ∥ AB . C     . A
    AEC     A C , 1  2, AEC A  ().       2 C   . ∥ (). AB ∥CD (). 22．如图，在平面直角坐标系中，三角形 ABC 的三个顶点分别 是 ( 1,6) A  ， ( 4, ) 3 B  ， (1,4) C .将三角形 ABC 先向右平移 4 个 单位，再向下平移 3 个单位，得到三角形 ' A B C . （1）请在图中画出平移后的三角形 ' ' （2）三角形 ' A B C 的面积是. A B C ； ' ' ' ' ' 23. 已知：实数 a ， b 满足 （1）可得 a  ，b  ； （2）当一个正实数 x 的两个平方根分别为 m a 和 2b m 时，求 x 的值. 3 ( b    0  . 4) a 2  24．已知：如图， AB ∥CD , AD 和 BC 交于点O ， E 为OC 上一点， F 为CD 上一点，   且 求证： EFC 证明： BOD  A   . CEF  180  . 25．2020 年 5 月 1 日新版《北京市生活垃圾管理条例》实施，意味着北京市垃圾分类正式 进入法治化、常态化、系统化轨道.条例明确规定，将垃圾分为厨余垃圾、有害垃圾、其他
    垃圾和可回收物 4 类. 为了帮助同学们养成垃圾分类的好习惯，七年级一班计划以此为主题 召开一次班会，需要一部分同学手绘可回收物的标识小卡片（如图）.发给大家的纸张和样 图中的纸张一样，都是边长为3 cm 的正方形. 为了让大家画的标志在纸张中的位置大小尽可能的一致.标志中标注了 A，B，C 三个关 键点，请你通过测量告诉大家 A，B，C 三点在纸张．．中的位置. 26. 在 平 面 直 角 坐标 系 xOy 中 ， 已 知 点  0A 0 a， ，  1A 1  a， ，  2A 2  0 1 a， ， … ， 2  A n a， ，    n n 0 B n， ，其中 0a ， 1a ， 2a ，…， na ，n 为正整数．顺次连接 0A ， 1A ， 2A ，…， nA ， B 的折线与 x 轴、 y 轴围成的封闭图形记为图形 M ．小明在求图形 M 的面积时，过  a， ，  2A 2 点  1A 1 边形，计算这些四边形面积的和，可以求出图形 M 的面积． a， ，…， 1 a  ， A n n    1  1  1 2 n 作 x 轴的垂线，将图形 M 分成 n 个四 图 1 图 2 备用图 请你参考小明的思路，解决下面的问题． （1）当 2n  时， 1 a ， ， 2 a ①若 0 a 1 3 2    ，如图 1，则图形 M 的面积为； ②用含有 0a ， 1a ， 2a 的式子表示图形 M 的面积为． （ 2 ） 当 4n  时 ， 从 1 ， 2 ， 3 ， … ， 10 这 10 个 正 整 数 中 任 选 5 个 不 同 的 数 作 为
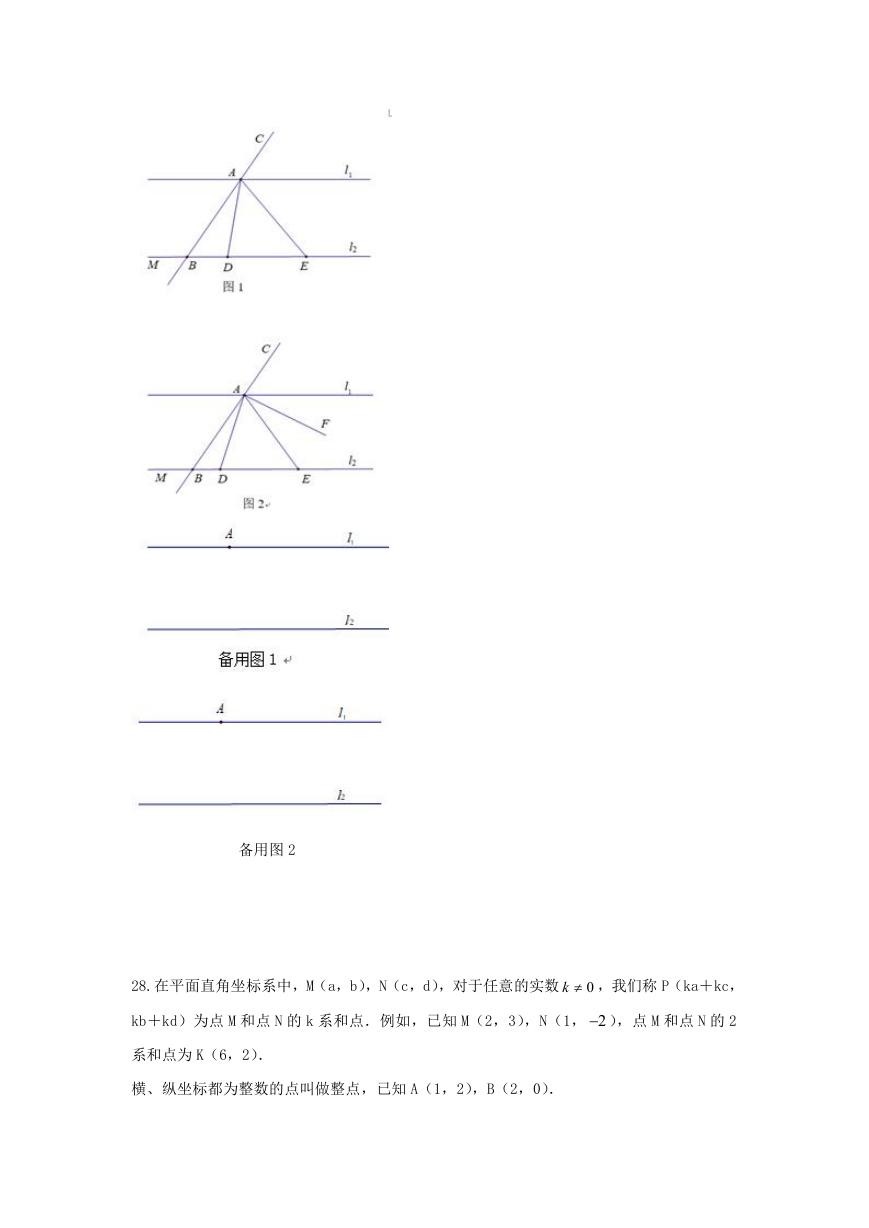
    a ， ， ， ， ． 0 a 2 a 4 a 3 a 1 a ①小明选择了 0  形 M ； 4 a ， ， 2 a 1  5  7 a ， 3  6 a ， 4  3 ，请在图 2 中画出此时的图 a ②在①的条件下，若小聪用剩下的 5 个数 1，2，8，9，10 作为 0 a ， ， ， ， 4 的取值，使新得到的图形 M 的面积与小明的图形 M 的面积相等，请直接写出 这五个数的排序（写出一组即可）． a 2 a 3 a 1 27. 已知：直线 1l ∥ 2l ，A 为直线 1l 上的一个定点，过点 A 的直线交 2l 于点 B，点 C 在线段 BA 的延长线上．D，E 为直线 2l 上的两个动点，点 D 在点 E 的左侧，连接 AD，AE，满足 ∠AED＝∠DAE．点 M 在 2l 上，且在点 B 的左侧． （1）如图 1，若∠BAD＝25°，∠AED＝50°，直接写出ABM 的度数； （2）射线 AF 为∠CAD 的角平分线． ① 如图 2，当点 D 在点 B 右侧时，用等式表示∠EAF 与∠ABD 之间的数量关系，并证明； ② 当点 D 与点 B 不重合，且∠ABM+∠EAF=150°时，直接写出∠EAF 的度数．
    备用图 2 28.在平面直角坐标系中，M（a，b），N（c，d），对于任意的实数 0 k  ，我们称 P（ka＋kc， kb＋kd）为点 M 和点 N 的 k 系和点．例如，已知 M（2，3），N（1， 2 ），点 M 和点 N 的 2 系和点为 K（6，2）． 横、纵坐标都为整数的点叫做整点，已知 A（1，2），B（2，0）．
    （1）点 A 和点 B 的 1 2 系和点的坐标为________（直接写出答案）； （2）已知点 C（m，2），若点 B 和点 C 的 k 系和点为点 D，点 D 在第一、三象限的角平分线 上. ①求 m 的值； ②若点 D 为整点，且三角形 BCD 的内部（不包括边界）恰有 3 个整点，直接写出 k 的值； （3）若点 E 与点 A 关于 x 轴对称，点 B 向右平移一个单位得到点 F，点 H 为线段 BF 上的动 点. 点 P 为点 A 和点 H 的 k 系和点，点 Q 为点 E 和点 H 的 k 系和点，k＞0.在点 H 运动过程 中，若四边形 AEQP 的内部（不包括边界）都至少有 10 个整点，至多有 15 个整点，则 k 的 取值范围为． 备用图 1 备用图 2
    分享到：
    赞 收藏

    相关推荐

    资料库

    初中一年级

    共收录374份资料，累计33个分类，关注成员有19位，主要包括：2023年,综合,上海,2022年,2020年,2021年,广东,河北,甘肃,天津,青海,新疆,2019年,北京,2016年,江苏,2011年

    热门标签

    2023年 综合 上海 2022年 2020年 2021年 广东 河北 甘肃 天津 青海 新疆 2019年 北京 2016年 江苏 2011年

    最新资料