论文研究-基于四元数ESPRIT的极化敏感阵列信号波达方向估计 .pdf-资料库

基于四元数 ESPRIT 的极化敏感阵列信号 http://www.paper.edu.cn 波达方向估计1 龚晓峰，徐友根，刘志文北京理工大学信息科学与技术学院电子工程系，北京 (100081) E-mail：mercury_gone@bit.edu.cn 摘要：在四元数代数体系下研究了极化敏感阵列信号波达方向（DOA）估计问题，提出一种四元数 ESPRIT 算法（Q-ESPRIT）。Q-ESPRIT 利用四元数矩阵低秩逼近对平移不变子阵的信号子空间进行估计，并通过挖掘不同子阵信号子空间之间的旋转不变关系，最终完成 DOA 估计。仿真结果表明，Q-ESPRIT 在短数据长度、低信噪比、以及存在模型误差等不利条件下的 DOA 估计性能明显优于传统的复数 ESPRIT 算法。关键词：四元数，极化，阵列信号处理，波达方向估计中图分类号：TN917.2 1．引言近十多年来，基于极化敏感阵列的信号波达方向（DOA）估计成为信号处理研究领域的热点问题之一，众多以往仅针对标量阵列的 DOA 估计算法（特别是子空间方法）已被成功地推广于极化敏感阵列[1-5]。由于极化敏感阵列能够感应入射信号的极化信息，其输出在局部具有矢量特性，基于极化敏感阵列的 DOA 估计算法比传统的标量阵列算法具有更高的精度。然而，现有方法大多将极化敏感阵列在不同空间位置上的多分量输出用一个复数长矢量进行组织。基于这种“复值长矢量”模型的算法，一定程度上破坏了阵列输出的局部矢量特性。近几年来，人们开始尝试用具有多个虚部的多元数（如四元数、双四元数）对矢量传感器（如交叉偶极子，三极子等）输出进行建模，通过将传感器输出矢量的各成分作为多虚部的系数，达到保留阵列输出局部矢量特性的目的[6-7]。但是，这些研究工作均围绕着 MUSIC 算法展开，其实用价值由于 MUSIC 算法的高运算量及角度估计的非解析形式而受到限制。在此，作者在四元数模型下，讨论基于 ESPRIT 算法的极化敏感阵列信号 DOA 估计问题。 2．四元数及四元数矩阵四元数及四元数矩阵的相关定义、性质及运算规则在文献[6]有详细讨论，这里仅介绍本文中将要用到的四元数和四元数矩阵的运算法则及性质。四元数[6] q ∈ H 由一个实部 0q ∈ R 和三个虚部 1 R 组成2： q q q ∈ , 3 , 2 虚部单位 i , , 满足如下关系： j k q = + + iq 1 q 0 jq 2 + kq 3 (1) ij = − = ji 则四元数还可表示为如下形式： ii k jk ; = = = − 1 i ki ; jj = − = kk kj = − = ik j (2) 1 本课题得到国家自然科学基金（No.60672084, No.60602037, No.60736006）的资助。 2 本文中， R 表示实数集合； l( )C 表示虚部单位为 l 的复数集合， l = , i , ； H 表示四元数集合。 j k -1-

http://www.paper.edu.cn q jq q 0 2 = + b 0 + i q jq ( 1 3 + b 1 ) (3) 其中 0 b b ∈ ( ) j C 。 , 1 同理，四元数矩阵 ∈Q H 可表示为： M N× Q Q 0 = + ⋅ + ⋅ i Q 2 j B 0 (4) Q ( 1 Q 3 ) + ⋅ j B 1 R ， × M N C ∈Q 其中阵的加法及乘法直接推广过来，特别的，由(2)式可得出四元数乘法不满足乘法交换率。 m = 。四元数矩阵的加法和乘法可由复矩， 0,1,...,3 ， 0,1 × )j M N ( ) ∈B m n = ( n 四元数矩阵 ∈Q H 的共轭转置记为 HQ ，定义如下： M N× H Q = Q T 0 − ⋅ − ⋅ − ⋅ k i j Q T 1 Q T 2 Q (5) T 3 这里‘T ’表示实矩阵转置。四元数矩阵 ∈Q H 的伴随矩阵 Qχ M N× ∈ C ( )i ( ) 2 M N× 2 如下定义： χ Q ⎡ B B ∗ ⎢ = ⎢ 0 1 −⎣ B B ∗ 0 1 ⎤ ⎥ ⎥ ⎦ (6) 这里‘ ∗ ’表示求复矩阵共轭， 0B ， 1B 由(4)式定义。记 M Ψ 单位矩阵，则有下面的式子成立： = [ I M , − ⋅ j I M ] ，其中 MI 为 M M× 的 −= Q 12 Ψ Ψ H M χ Ψ Ψ H N Q H N Ψ χ Ψ = M Q I 2 M = Ψ Ψ χ M Q H M M N (7) 由于四元数矩阵同其伴随矩阵具有相似的性质，其运算法则大多可由伴随矩阵的相应运算计算得到（譬如四元数矩阵乘法、特征分解等）[6]，进而通过伴随矩阵可将四元数矩阵运算转化为复矩阵运算。作者接下来介绍如何通过复矩阵运算实现四元数矩阵求逆及特征分解。假设存在四元数方阵 , ∈Q P H ，满足 M M× QP = PQ I ，则 P 和 Q 互为逆矩阵，Q 的逆 = M 矩阵记为 1−Q 。记 1 , −Q Q 的伴随矩阵分别为 Qχ 和 1Q−χ ，则由(7)式： − 1 QQ = = = 2 2 1 − 2 − 2 − 2 − 1 Q H M Q M ⋅ Ψ χ Ψ Ψ χ Ψ H M ⋅ Ψ χ χ Ψ Ψ Ψ H M M ⋅ = Ψ χ χ Ψ I M H M H M M Q M Q − 1 Q M − 1 Q (8) 将 MI 看作是特殊的四元数矩阵（所有虚部的系数都为零），(8)式表明 χ χ 为 MI 的伴随矩 Q Q− I ，即 Qχ 和 1Q−χ 互为逆矩阵。则可利用复矩阵求逆得到 Qχ M 2 1 阵，由伴随矩阵定义有 χ χ Q Q− = 1 的逆矩阵 1Q−χ ，进而由(4)式及(6)式求得 1−Q 。假设存在四元数方阵 ∈Q H ，则其伴随矩阵 Qχ 可特征分解为： M M× =χ Q V D V (9) C H C C -2-

http://www.paper.edu.cn 其中复对角矩阵 ∈D ( (2 M M × 2 量矩阵 V C = [ v 1 ,..., ] M 2 (2 M M )j ( ) C ∈ ( )j ( ) C C v ) 对角线上的第 n 个元素 nξ 为 Qχ 的第 n 个复特征值，特征向 × 2 ) ， nv 为 Qχ 对应于特征值 nξ 的特征向量。 M ，这里 1,..., m ξ = 。并且，若将 mξ ξ + 对应的特征向量为。则 m M 可以证明， Qχ 的特征值成共轭对出现的，即 v , 对应的特征向量表示为 = − v [ , m ξ += * m M C ∈ )j ( ( ) m T m v ， T m v 。由此，可以将 CD 和 CV 写成如下形式： ] T × 1) v M ,0 ,0 m m ,1 ,1 ( v + = m M [( v * m ,1 ) ,( T v * m ,0 ) ] T T D C = D ⎡ ⎢ ⎢ ⎣ ⎤ ⎥ ⎥ ⎦ * D , V C ⎡ V V * ⎢ = ⎢ 0 1 − V V * ⎣ 0 1 ⎤ ⎥ ⎥ ⎦ (10) [ v 1,0 , v 2,0 ,..., v ， 1 ]M ,0 =V [ v 1,1 , v 2,1 ,..., v 。比较(9)式和(6)式，可知 CD ]M ,1 这里 D ξ 1 ⎡ ⎢ ⎢ = ⎢ ⎢ ⎣ ， 0 =V ⎤ ⎥ ⎥ ⎥ ⎥ ⎦ M ∈D C ( M M× ξ 和 CV 分别为元数方阵 V V 0 ∈Q H 的特征分解： )j ( ) M M× 和 = + ( ) i V 1 ∈ H ( M M× ) 的伴随矩阵。则由(7)式和(9)式可得到四 =Q VDV (11) H 对于厄米特的四元数矩阵 ∈Q H 而言3， D 为实对角阵[6]。 M M× 3. 四元数 ESPRIT 3.1 极化敏感阵列四元数模型 ( n d− ， d 为相邻阵元间距， 0 考虑 N 个交叉偶极子天线在 x 轴上均匀排列组成极化敏感阵列（如图 1 所示），第 n 个阵元在 x 轴上的坐标为 1 ) 。组成每一个阵元的两个偶极子天线分别和 x ， y 轴平行，分别感应入射电场在 x 与 y 轴方向的分量。由文献[2]，对于一个在 x - z 平面内由角度 θ 入射的窄带远场完全极化信号，记其在坐标元点处的电场强度为 E ，则 x 与 y 方向的电场强度 xE 与 yE 的表达式分别为： = ⋅ E (12) cos sin = ⋅ E =n ,..., cos γe E E 3 θ γ ⋅ j η , y x 这里 0 γ π / 2 ≤ ≤ 和 π 用一个四元数 e ∈ H 表示 xE 和 yE ： − ≤ ≤ 分别为极化幅角与极化相位差。 π η e = = E x γ (cos cos ) + ⋅ i E y γ θ e sin p θ γ η , , + ⋅ i η ⋅ j (13) E 假设 x 与 y 轴方向电偶极子的输出分别正比于入射信号在该位置处电场矢量的 x 与 y 分量，且该比例系数等于一。则阵列的响应为： x θ γ η , , = T ⎤ p ⎥ ⎦ θ γ η , , ,..., ⎡ ⋅ ⎢ ⎣ )sin )sin πd 1 e e πd (2 (2 θ θ λ λ N j j / / a θ γ η , , E (14) 3 四元数方阵见(5)式。 ∈Q H 若满足 H =Q M M× Q ，则称其为厄米特四元数矩阵。这里‘ H ’表示四元数矩阵共轭转置， -3-

http://www.paper.edu.cn ( N × 1) ∈ 这里 a θ γ η , , H 为阵列导向矢量， nd 为第 n 个阵元在 x 轴上的坐标， 1,..., 波长。在均匀线阵的情况下，并假设阵列第一个阵元位于坐标原点， 0 e [ − ，则(14)式可写成： 1 ] θ n = πd λ / )sin n (2 j ， λ 为信号 N d = ， nd = 0 x θ γ η , , = 这里 θq e= j (2 πd λ / )sin θ 为空间相位因子。 − 1 T ⎤ p ⎥ ⎦ θ γ η , , q N θ ⎡ ⋅ ⎢ 1,..., ⎣ a θ γ η , , E (15) 信号入射方向 y z θ o d 图 1.交叉偶极子阵列 Fig.1 Array of crossed dipoles x 考虑 M 个完全极化的远场窄带信号在 x - z 平面以不同的角度入射的情况，第 m 个信号 θ γ η ， m = 1 M,..., 。则阵列输出的入射角及极化参数为 , m , m m ∈z t ( ) H 可以表示为： × 1) N ( M ∑z t ( ) = m = 1 a θ η m m m γ , , s m t ( ) + n t ( ) = As t ( ) + n t ( ) (16) , , , 1 ) γ ] t ( ) θ γ η , 1 1 + j ωt φ ( m θ η m m m e m a = E ,..., 这里 =A [2]，ω 为载波频率， mE 和 mφ 分别为第 m 个信号在原点处的电场及相位；， ( )t =s s m a [ 记四元数矩阵 A 的前 1N − 行组成的子矩阵为 1A ，A 的最后 1N − 行组成的子矩阵为 2A ，并按照类似的方式得到阵列输出矢量 ( )tz 的子矢量 1( )tz 与 2( )tz ，以及噪声矢量 ( )tn 的子矢量 1( )tn 与 2 ( )tn ，则有： t 。 ( )]T ( ),..., s t 1[ s M z 1 z 2 t ( ) t ( ) = = 并且由 A 的定义及(15)式，可以得到： A s 1 A s 2 t ( ) t ( ) + n 1 + n 2 t ( ) t ( ) (17) A 2 q θ 1 ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ = ⎢ A ⎥ 1 ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ q θ M Φ (18) 3.2 所提算法四元数 ESPRIT 算法（Q-ESPRIT）的基本思想在于用四元数矩阵运算完成 ESPRIT 算法 -4-

的基本步骤，以实现 DOA 估计。算法步骤如下：计算 ( )tz 的样本协方差矩阵： http://www.paper.edu.cn R T = ∑ T − 1 n = 1 z t ( n H ) z t ( n ) (19) 这里T 为快拍数。根据第一节所介绍的四元数矩阵特征分解对 R 进行特征分解，并取最大的 M 个特征值对应的特征矢量（四元数矩阵的低秩逼近[6]），可得到信号子空间的估计值 Ε ，取 Ε 的前 1N − 行以及最后 1N − 行组成 1 ,Ε Ε 之间满足如下关系： ,Ε Ε 。由信号子空间的定义， 1 ,A A 与 1 2 2 2 这里 M M× ∈T H 为四元数方阵。 ,Ε Ε 满秩，存在矩阵由于 1 2 E 1 E 2 = = AT 1 A T 2 = A ΦT 1 (20) ∈Ω H ： M M× = ⇒ E Ω E 1 2 = ATΩ A ΦTΦ 1 TΩ ΦT ⇒ = 1 (21) 这里 Ω 可由第一节中所介绍的四元数矩阵求逆运算得到： =Ω ( E E H 1 1 1 − ) E E (22) H 1 2 由(21)式进一步得到： H Ω T H = H T Φ 。若记 H H =T t 1[ ,..., t ，则有： M ] Ω t H m m θq= * m t (23) 这里 1,..., m = M 。(23)式表明 * 一节中介绍的四元数矩阵特征分解可求得 * mθq 是四元数方阵 HΩ 的特征值， mt 是 HΩ 的特征向量。利用第 mθq 的估计值。进而，由(15)式中关于空间相位因子的定义，可最终得到入射信号的 DOA 估计。由上述步骤不难看出，ESPRIT 算法的性能优劣取决于信号子空间的估计精度。而通过四元数矩阵的低秩逼近，以获得比传统方法更为精确的信号子空间估计[6]，正是 Q-ESPRIT 的优势所在。这一特点，也使得 Q-ESPRIT 在存在模型误差、低信噪比及低快拍数的情况下，较之传统算法具有更好的性能。 4. 仿真结果考虑 3 个非相关窄带信号入射至一个 8 元交叉偶极子均匀线阵，阵元间距为半波长；信 ) ， 10=θ 号 DOA 分别为： 1 = γ η γ η ) ) ， 3 ( , ( , 2 3 2 首先考察 Q-ESPRIT 和传统的复数 ESPRIT 算法（C-ESPRIT）性能随模型误差的变化。 γ η ( , ；极化参数分别为： 1 1 30=θ ， 2 44 60 ( , 45=θ 33 45 ( 22 30 ) 。， 3 = = ) ( , , ) 假定阵列存在如下未知模型误差： d n = + / P ε 1 2 ε d n (24) n -5-

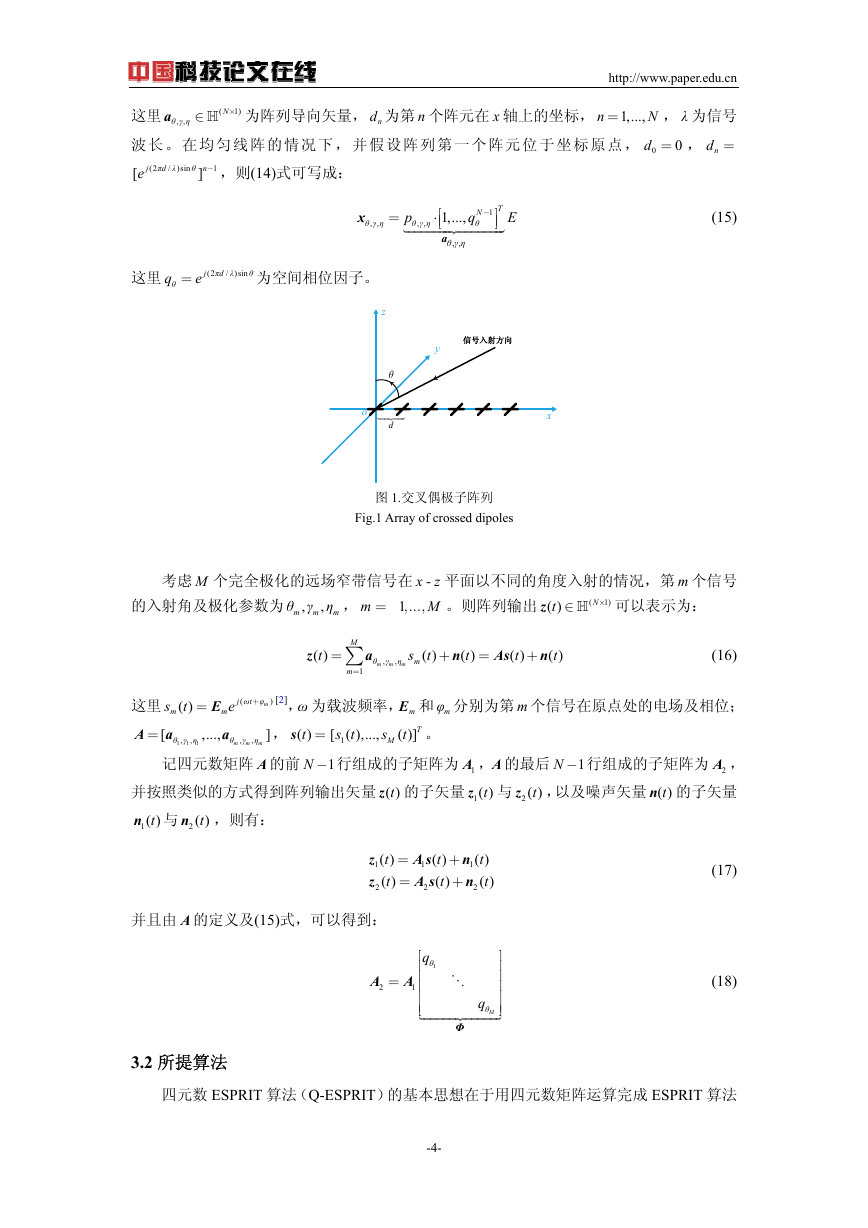
其中 nd 和 nd 分别为第 n 个阵元在 x 轴上的理想坐标值及实际坐标值， nε 为零均值、单位方差的高斯随机变量， 1 = ,..., ， Pε 为模型误差方差。模型误差示意图由图 2 给出。 N n http://www.paper.edu.cn d P⋅ e d 实际阵元位置理想阵元位置图 2.阵列模型误差 Fig.2 Array model error 固定信噪比为 30dB，快拍数为 1000。Q-ESPRIT 和传统的 C-ESPRIT 性能曲线见图 3，其中横坐标为模型误差方差 Pε ，纵坐标为入射信号均方根误差（RMSE）的平均值（总体均方根误差）。可以看到，Q-ESPRIT 比 C-ESPRIT 具有更好的模型误差鲁棒性。 8 7 6 5 4 3 2 1 四元数ESPRIT 传统ESPRIT ) ( 度差误根方均体总 -6- 0 0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045 0.05 图 3. 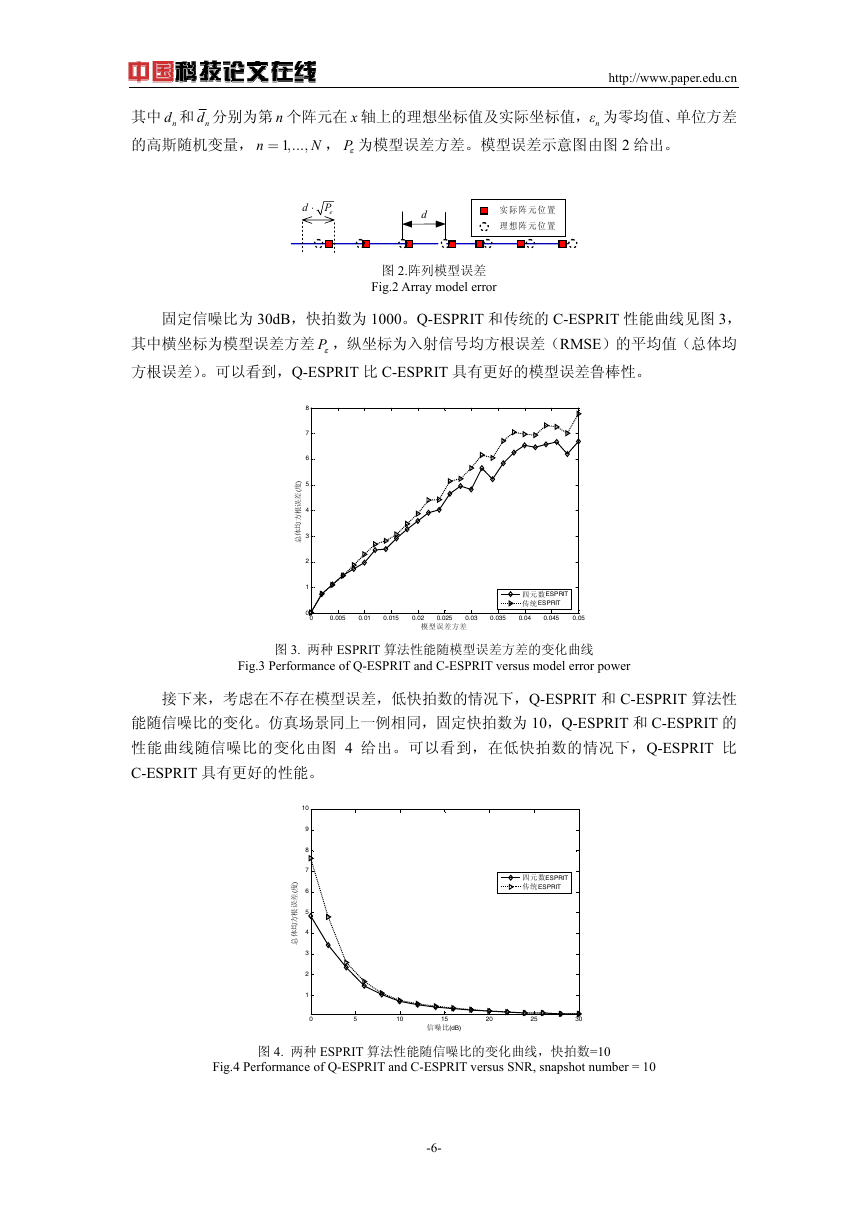两种 ESPRIT 算法性能随模型误差方差的变化曲线模型误差方差 Fig.3 Performance of Q-ESPRIT and C-ESPRIT versus model error power 接下来，考虑在不存在模型误差，低快拍数的情况下，Q-ESPRIT 和 C-ESPRIT 算法性能随信噪比的变化。仿真场景同上一例相同，固定快拍数为 10，Q-ESPRIT 和 C-ESPRIT 的性能曲线随信噪比的变化由图 4 给出。可以看到，在低快拍数的情况下，Q-ESPRIT 比 C-ESPRIT 具有更好的性能。四元数ESPRIT 传统ESPRIT 10 9 8 7 6 5 4 3 2 1 ) ( 度差误根方均体总 0 5 10 15 信噪比(dB) 20 25 30 图 4. 两种 ESPRIT 算法性能随信噪比的变化曲线，快拍数=10 Fig.4 Performance of Q-ESPRIT and C-ESPRIT versus SNR, snapshot number = 10

http://www.paper.edu.cn 5. 结论提出了一种新的极化敏感阵列信号 DOA 估计算法—四元数 ESPRIT，理论分析和仿真结果表明，四元数 ESPRIT 算法比传统的复数 ESPRIT 算法具有更高的模型误差鲁棒性，并且在低快拍数、低信噪比等不利条件下具有更好的 DOA 估计性能。参考文献 [1] R T Compton, Jr. The tripole antenna: an adaptive array with full polarization flexibility [J]. IEEE Trans. on Antennas Propagation, 1981, 29(6): 944-952. [2] J Li and R T Compton, Jr. Angle and Polarization Estimation Using ESPRIT with a Polarization Sensitive Array [J]. IEEE Trans. on Antennas Propagation, 1991, 39(9): 1376-1383. [3] A Nehorai and E Paldi. Vector-sensor array processing for electromagnetic source localization [J]. IEEE Trans. on Signal Processing, 1994, 42(2): 376-398. [4] K T Wong. Direction finding/polarization estimation-dipole and/or loop triad(s) [J]. IEEE Trans. on Aerospace, & Electronic. Systems, 2001, 37(2): 679-684. [5] 徐友根, 刘志文. 基于累积量的极化敏感阵列 DOA 和极化参数的同时估计 [J]. 电子学报, 2004, 32(12): 1962-1966. [6] S Miron, N Le Bihan and J Mars. Quaternion-MUSIC for vector-sensor array processing [J]. IEEE Trans. on Signal Processing, 2006, 54(4): 1218-1229. [7] N Le Bihan, S Miron and J Mars. MUSIC algorithm for vector-sensors array using biquaternions [J]. IEEE Trans. on Signal Processing, 2007, 55(9): 4523-4533. Quaternion-ESPRIT for Direction of Arrival Estimation with Array of Crossed Dipoles Gong Xiaofeng, Xu Yougen, Liu Zhiwen School of Information Science and Technology, Department of Electronic Engineering, Beijing Institute of Technology, Beijing, PRC (100081) Abstract The problem of direction of arrival (DOA) estimation with polarization sensitive arrays is addressed within the quaternionic framework, and a new ESPRIT variant, termed as quaternion-ESPRIT (Q-ESPRIT), is proposed. The proposed algorithm estimates the signal subspace of an array of translational invariance structure via quaternionic low-rank approximation, and exploits the underlying rotational invariance between signal subspaces of different subarrays to obtain the ultimate DOA estimates. Simulation results show that Q-ESPRIT significantly outperforms its conventional counterpart in extremely difficult situations with short data length, low signal to noise ratio, or unknown model errors. Keywords: Quaternion, polarization, array signal processing, direction of arrival estimation. 作者简介：龚晓峰，男，1981 年生，博士研究生，主要研究方向是阵列信号处理及其应用。 -7-

资料库

论文研究-基于四元数ESPRIT的极化敏感阵列信号波达方向估计 .pdf

相关推荐

开发技术

热门标签

最新资料