中国科技论文在线 http://www.paper.edu.cn 解对流扩散方程的 ADI 方法及其应用 李海龙1，戴林超2，张磊1** （1. 中国矿业大学（北京）理学院，北京 100083； 2. 中国矿业大学（北京）资源与安全工程学院，北京 100083） 摘要：运用交替方向隐式格式（ADI 方法）对典型的二维对流扩散方程进行了数值求解，并 利用编程软件 C、Matlab 结合实例进行了数值模拟研究。结果表明：ADI 方法具有运算速度 快、收敛性好、精度高等特点，具有良好的应用前景。 关键词： 对流扩散方程；交替方向隐式格式（ADI 方法）；数值模拟 中图分类号：O246 ADI Solution of Convection Diffusion Equation and Its Application Li Hailong1, Dai Linchao2, Zhang Lei1 (1. School of Science, CUMTB, Beijing 100083; 2. School of Resources and Safety Engineering,CUMTB,Beijing 100083) Abstract: Alternating direction implicit scheme (ADI method) is used to numerically solve the typical two-dimensional convection-diffusion equation ,and the programming software of C and Matlab combined with a practical is used to study numerical simulation. The results showed that: ADI method has fast speed , good convergence, high precision and good prospects. Keywords: convection diffusion equation;ADI method;numerical simulation 1 引言 对流扩散方程是表征流动系统质量传递规律的基本方程，求解此方程可得出浓度分布情 况，其数值计算方法的研究一直受到人们的广泛重视。选取合适的数值计算方法进行求解具 有重要的理论和实际意义。考虑以下具有特殊边值条件的二维对流扩散方程： = k ⎛ ⎜ ⎝ ∂ ∂ 2 ⎞ ρ ρ ⎟ x 2 2 ⎠ 2 ∂ y ∂ + + Q x y ( , ) x y t ( , , ) ∈ Ω× J x y , ∈ Ω x y t , ) ( , ∈∂Ω× J （1） v u + + ⎧ ∂ ∂ ρ ρ ρ ∂ ⎪ y t x ∂ ∂ ∂ ⎪ ⎪ x y ,0) 0 ( , ρ ⎨ ⎪ x y t , ) 0 ( , ρ ⎪ ⎪⎩ 其中 = = 2RΩ∈ 为具有C 边界的有界区域∂Ω ，且 (0, = J T ], T > 。 0 方程（1）在工科数值模拟计算中具有广泛的应用，尤其在描述各种物质的浓度等扩散 过程的物理现象中有极为重要的作用。目前，在研究如何利用用有限差分法解其中的对流占 优扩散方程时，必须要考虑到解对流占有扩散方程时经常遇到的问题：非物理震荡和数值扩 散[1,2]，所以选取合适的数值计算方法，从而合理解决上述谈到的问题是非常重要的。基于 此，本文选用交替方向隐式格式（ADI 方法）[3,4]来求解二维对流扩散方程，此方法除有效 作者简介：李海龙（1988-），男，主要研究方向：数值计算 通信联系人：戴林超（1987-），男，硕士，主要研究方向：安全技术及工程. E-mail: dailinchao@126.com - 1 - 

j + k = l x Δ H y Δ v τ y 4 Δ 中国科技论文在线 http://www.paper.edu.cn 的解决了上述问题之外，更有其他方法所没有的优点：计算速度快，加快收敛速度，是一种 稳定、高效的数值算法。 2 交替方向隐式格式 在对方程（1）进行求解时，考虑到用隐式方法求解二维问题得到的线性方程组其系数 矩阵为宽带状，所以求解起来很不方便，因此本文采用 ADI 方法来求解，并且此格式是无 条件稳定的[2]。具体过程可分为两步，第一步先求出第 n 层与第 1+n 层的中间值： n ρ ρ i j , 1 2 n i , + j τ n ρ i 1, + − / 2 − j k + u n i 1, + n ρ ρ i 1, − x − Δ j 2 j + v + 2 n n ρ ρ i j i , 1, − x 2 Δ n ρ i j , 1 + 1 n + ρ 2 i j 1, + − = k 1 2 1 n n + + 2 ρ ρ 2 i j i j 1, , − x 2 Δ + 2 + （2） 1 − n i j , n − ρ ρ i j , y Δ + 1 + 2 2 n n ρ ρ i j i j , , y 2 Δ − 1 − 式中： 0 ≤≤ NNj , ，l 为巷道长度， xΔ 为模拟巷道长度时所分的步长； 0 ≤ ≤ i M M , = ， H 为巷道宽度， yΔ 为模拟巷道宽度时所分的步长。 , , , 4 2 n p q = = = 设 k τ y 2 Δ 1 n + p ρ 2 i j 1, − um τ = x 4 Δ ，则上式可化简整理为 k τ x 2 Δ 1 n + p n ) ( + ρ = ρ 2 j i j i 1, 1, + + n q m p ( ( + − − + − j N 1M − 循环，则都能得到系数矩阵为三对 1, − 令i 从 1 到 角矩阵的线性方程组，其系数矩阵均为 q n 2 1) − ρ i j , n q ) ( n + − − ρ i j , 对式（3）中每一个 2 m p − ) n ρ i 1, − + − − p ( 1 2 ) p (2 ) n ρ i j , （3） ≤ ≤ n ρ i , + + + j 1 2 1 + 1 − j p 1 2 − − p A ⎛ ⎜ ⎜ ⎜ = ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ p p p 1 2 − − p 1 2 − − p ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ p p 1 2 − − p （4） 对每一个 j 解三对角线性方程组即可得一列的中间值，最终将得到除某些边 界值的所有中间值，然后将这些边界值取与之最接近的已求得的中间值，这样就 得到了所有 M N× 的网格上的中间值，此时就可以进行第二步： 1 2 n + n 1 + − ρ ρ i j i j , , / 2 τ 1 n + ρ ρ 2 i j 1, − x 1 n + − 2 i j 1, + 2 Δ 1 n + ρ ρ 2 i j , 1 − y 1 n + − 2 i j , 1 + 2 Δ + v + u 1 n + ρ 2 i j 1, + − = k m 设 1 = u τ x 4 Δ , n 1 = v τ y 4 Δ , p 1 = n 1 + ρ i 1, + k j + − n n 2 1 1 + + ρ ρ i j i 1, , − y 2 2 Δ k τ x 2 2 Δ k τ y 2 Δ q 1 = 4 , - 2 - 1 2 + 1 n n + + 2 ρ ρ 2 i j i j 1, , − x 2 Δ 1 n n + + 2 ρ ρ 2 i j i j , , 1 − y 2 Δ + 1 2 2 + （5） 1 n + ρ 2 i j , 1 + − j + k ，则上式可化简整理为： 

中国科技论文在线 http://www.paper.edu.cn ( − = m p 1 1 1 n + ) ρ 2 i j 1, − 1 n + ) ρ 2 i j 1, + + (2 1 n + ) ρ 2 i j , 1 + p 1 + 2 q 1 − 1 2 1) n + ρ i j , 1 n + ) ρ 2 i j , 1 − （6） q n 1 + ρ i j 1 1 , − + − − q ( 1 2 ) 1 n 1 + ρ i j , + q n 1 + ρ i j 1 1 , + 对式（6）中每一个 2 m p n q ( − − + − 1 1 1 1 − 令 j 从 1 到 i N 1M − 循环，则都能得到系数矩阵为三对 1, ≤ ≤ + − − q 1 n 1 + ( ( 角矩阵的线性方程组。其系数矩阵均为 q 1 1 2 − − q 1 A ⎛ ⎜ ⎜ ⎜ = ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ q 1 q 1 q 1 1 2 − − q q 1 2 − − 1 1 q 1 ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ （7） q 1 1 2 − − q 1 对每一个i 解三对角线性方程组即可得一列所求值，最终得到所有第 1+n 层的所有值。 至此，便完成了一个时间单位上的计算，即由第 n 层得到第 1+n 层的值，又由题中条 件知当n =0 时所有值为 0，这样对n 循环就可以求出所有时间所有坐标的值。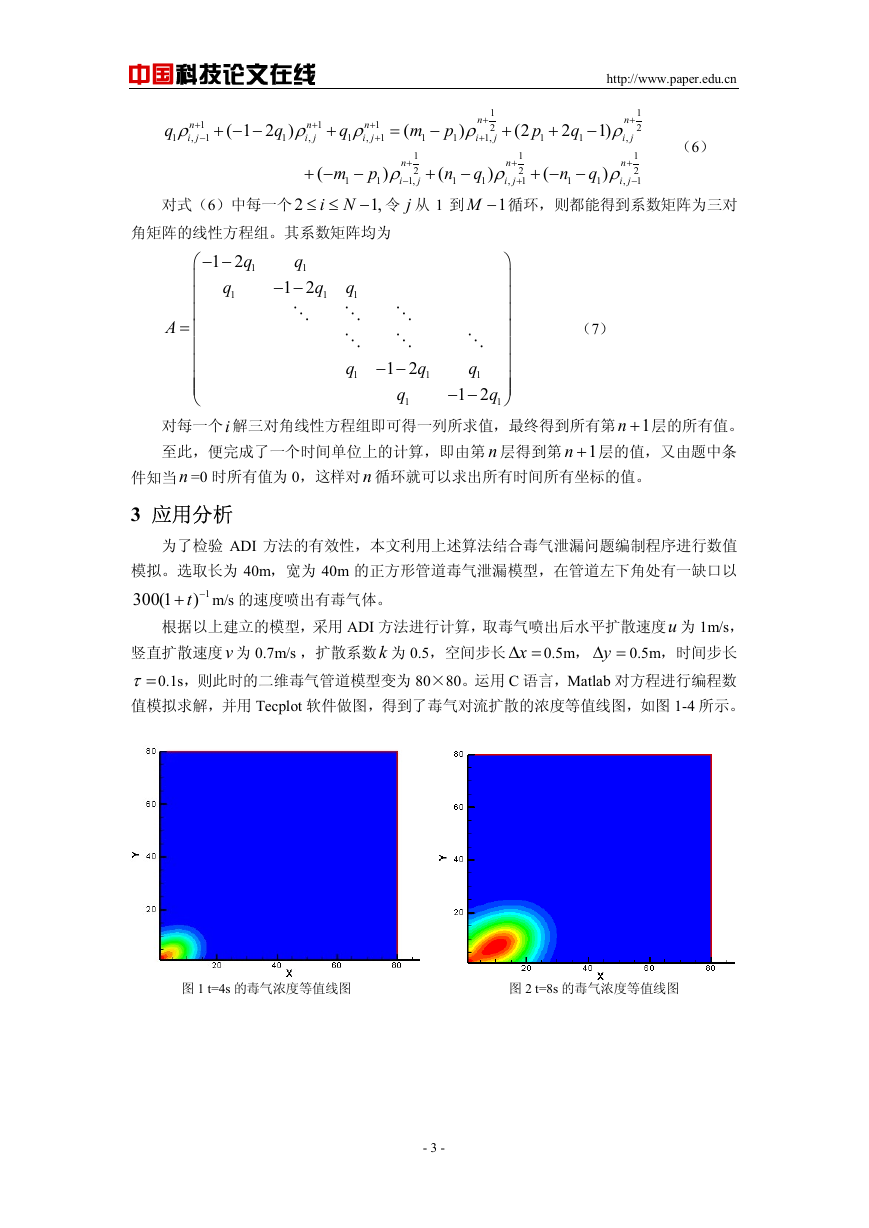 3 应用分析 为了检验 ADI 方法的有效性，本文利用上述算法结合毒气泄漏问题编制程序进行数值 模拟。选取长为 40m，宽为 40m 的正方形管道毒气泄漏模型，在管道左下角处有一缺口以 1(300 −+ t m/s 的速度喷出有毒气体。 1) 根据以上建立的模型，采用 ADI 方法进行计算，取毒气喷出后水平扩散速度u 为 1m/s， 竖直扩散速度v 为 0.7m/s ，扩散系数k 为 0.5，空间步长 =Δx 0.5m，时间步长 =τ 0.1s，则此时的二维毒气管道模型变为 80×80。运用 C 语言，Matlab 对方程进行编程数 值模拟求解，并用 Tecplot 软件做图，得到了毒气对流扩散的浓度等值线图，如图 1-4 所示。 0.5m， =Δy 图 1 t=4s 的毒气浓度等值线图 图 2 t=8s 的毒气浓度等值线图 - 3 - 

中国科技论文在线 http://www.paper.edu.cn 图 3 t=16s 的毒气浓度等值线图 图 4 t=24s 的毒气浓度等值线图 再者，在计算时间上，将本文计算所用时间与文献秦新强[7] 等计算的结果相比较，对 比结果如表 1 所示。 计算精度 0.166666 0.1 表 1 ADI 方法与两重网格算法的计算时间比较表 CPU 时间(文献[7]) CPU 时间(本文) 10.6” 165.9” 8.55” 158.5” 从表 1 中可以看出，在同一误差水平下，ADI 方法比两重网格算法具有计算速度更快的 优点，更适合用于对流扩散方程的求解。 4 结论 本文利用 ADI 方法来求解二维对流扩散方程，并结合实例验证了此方法的有效性。通 过上述讨论及与前人结果对比可知：ADI 方法其关键就在于“交替方向”，因为其将要解的 系数矩阵为宽带状的线性方程组转换成了容易求解的系数矩阵为三对角矩阵的线性方程组， 故而提高了计算速度，是解对流扩散方程的一种稳定性好、消除了数值震荡等现象、计算速 度快的方法，是一种值得推广的稳定、高效的算法。 [参考文献] (References) [1] Douglas J,J R, Russel T F. Numerical methods for convection-dominated diffusion problems based on combining the method of charcateristics with finite element or finite difference prcedures[J].SIAM J Numer Anal,1982,19(5):871-885 [2] 陆金甫,关治.偏微分方程数值解法(第二版)[M]. 北京:清华大学出版社,2003. [3] 张廷芳.计算流体力学[M].大连:大连理工大学出版社,2007:257-259 [4] 张文生.科学计算中的偏微分方程有限差分法[M].北京:高等教育出版社,2006:258-261,312-314 [5] 袁兆鼎,费景高,刘德贵.刚性常微分方程初值问题的数值解法[M].北京:科学出版社,1987 [6] 李庆扬,王能超,易大义.数值分析(第四版)[M].北京:清华大学出版社,Springer 出版社,2001 [7] 秦新强,党发宁,龚春琼等.二维非线性对流扩散方程的特征混合有限元两重网格算法[J].计算机技术及发 展,2009,19(7):137-140 - 4 -