logo资料库

2022-2023学年山西省运城市八年级上学期期中数学试题及答案.doc

发布时间：2023-10-13 发布人：admin 分类：说明书 资料大小：1.61M 资料格式：doc 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    2022-2023 学年山西省运城市八年级上学期期中数学试题及答案 注意事项： 1．答卷前务必将自己的班级、姓名、考号填写在答题卡上． 2．考试结束后，监考人员将答题卡收回． 一、选择题（本题共 10 个小题，每小题 3 分，共 30 分，请将每题中唯一正确答案的序号填入题前的方框 内） 1． 3 的相反数是（ ） A． 3 2．在实数 5 ， B． 3 π 2 ， 4 ， 22 7 中，无理数有（ ） C． 3 3 D．  3 3 ，3.14159， 3 8 ，0.232332332……（每相邻两个 2 之间依次多一个 3） A．4 个 B．3 个 C．2 个 D．1 个 3．河东池盐业博物馆位于运城市盐湖区盐池的北岸，当地人习惯称之为“池神庙”．它也是我国惟一保存 良好的盐神庙．站在池神庙高处俯瞰，“千古中条一池雪”的诗景美不胜收．如图是河东池盐业博物馆的 平面图，已知池神庙的位置是 0,0 ，老火车遗址的位置是 ，则盐湖生态公园的位置是（ ） 6,2 2,4 B． A． 2,4 4．下列计算中，正确的是（ ） A． 2 C．  2  5 3 5  2  3 C． 2, 4  D． 2, 4    B． 2 D． 2   3 6   3 2   3 1   5．全红婵在出征 2022 年国际泳联跳水世界杯前刻苦进行跳水训练，教练对她 20 次的训练成绩进行统计分 析，判断她的成绩是否稳定，则教练需要知道全红婵这 20 次成绩的（ ） A．众数 B．平均数 C．频数 D．方差 6．法国数学家笛卡尔（Descartes，1596—1650），最早引入平面直角坐标系，用代数方法研究几何，这 种研究方法体现的数学思想是（ ） A．数形结合 B．建模 C．类比 D．分类讨论 学科 网（北 京）股 份有限 公司
    到 x 轴的距离是 3 ，则直线 AB x∥ 轴 ,P a b 表示原点 2,2 7．在平面直角坐标系中，下列说法正确的是（ ） 3,2 A．点  P ab  ，则点  0 B．若 、  C．若  2,2 B A  D．点   23, 1 a P  所在象限是第四象限 中， A ， B ， C 的对边分别记为 a ，b ， c ，下列结论中不正确的是（ ） 8．在 ABC△ A．如果 A B．如果 : A C．如果 1a  ， D．如果 2 2 b a 9．如图，数轴上点 A 、 B 对应的数分别是 1，2，过点 B 作 PQ AB ，以点 B 为圆心， AB 长为半径作 圆弧，交 PQ 于点C ，以原点O 为圆心，OC 长为半径画弧，交数轴于点 M ，当点 M 在点 B 的右侧时， 点 M 对应的数是（ ） C B      ，那么 ABC△ : B C     2 b  ，  ，那么 ABC△ c 是直角三角形 90  A  1: 2:3 ，那么 ABC△ 3 c  ，那么 ABC△ 是直角三角形且  2 是直角三角形 是直角三角形 B． 2 1 C． 2 2 D． 5 A． 2 10．如图， ABC△ 论正确的有（ ） BCD ① ACE △ ≌△ 90 ADB  ③  和 ECD△ 都是等腰直角三角形， ABC△ 的顶点 A 在 ECD△ 的斜边 DE 上，下列结 ② DAB  ④ 2 AE    2 AD ACE 2  AC 2 A．1 个 B．2 个 C．3 个 D．4 个 二、填空题（本大题共 5 个小题，每小题 3 分，共 15 分） 11．计算 20  的结果等于______． 1 5 1,3 关于 x 轴对称的点的坐标为______． 12．点 13．党的二十大于 2022 年 10 月 16 日在北京开幕．某校选拔了一名教师参加市里举办的《喜迎二十大，奋 进新征程》演讲比赛．比赛从演讲内容、语言表达、神情动作、仪表形象四个方面按照 30%，40%，20%，10% 学科 网（北 京）股 份有限 公司
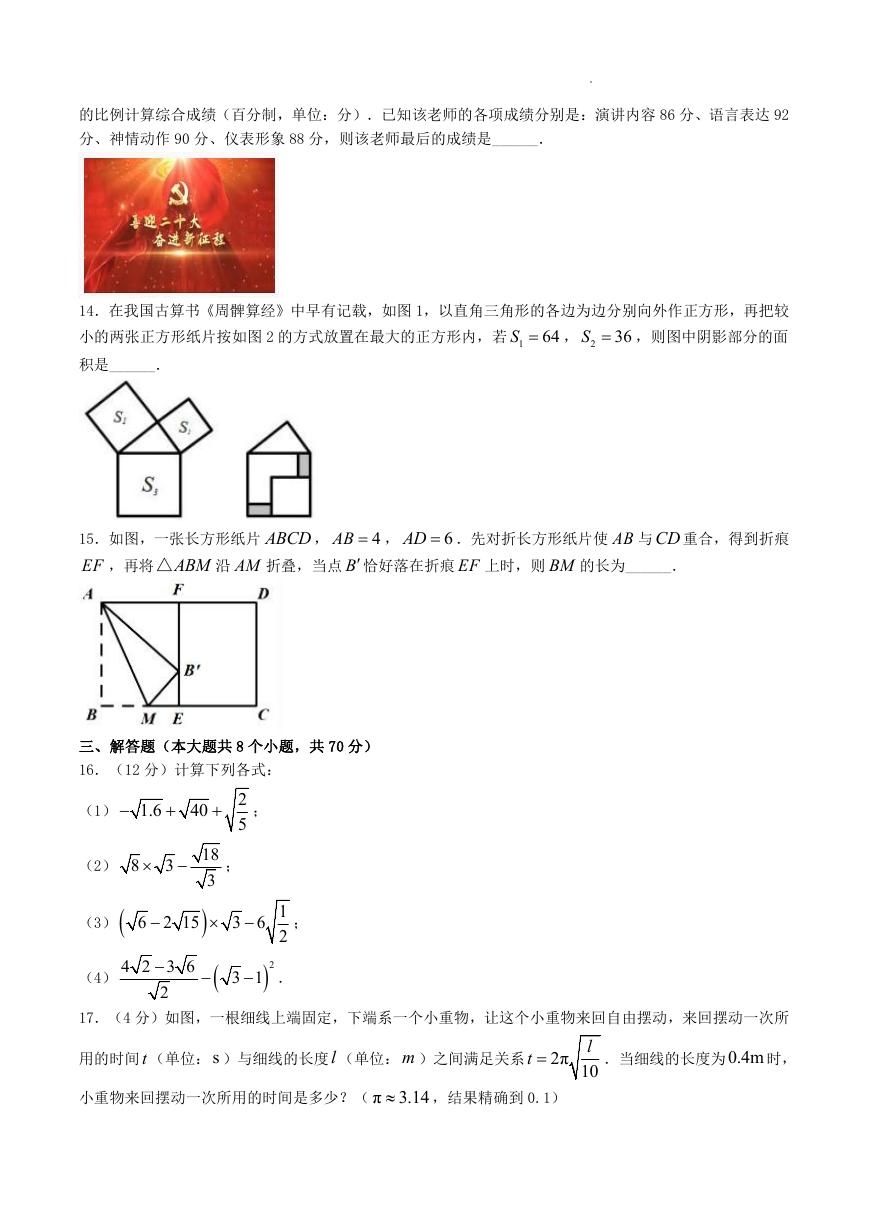
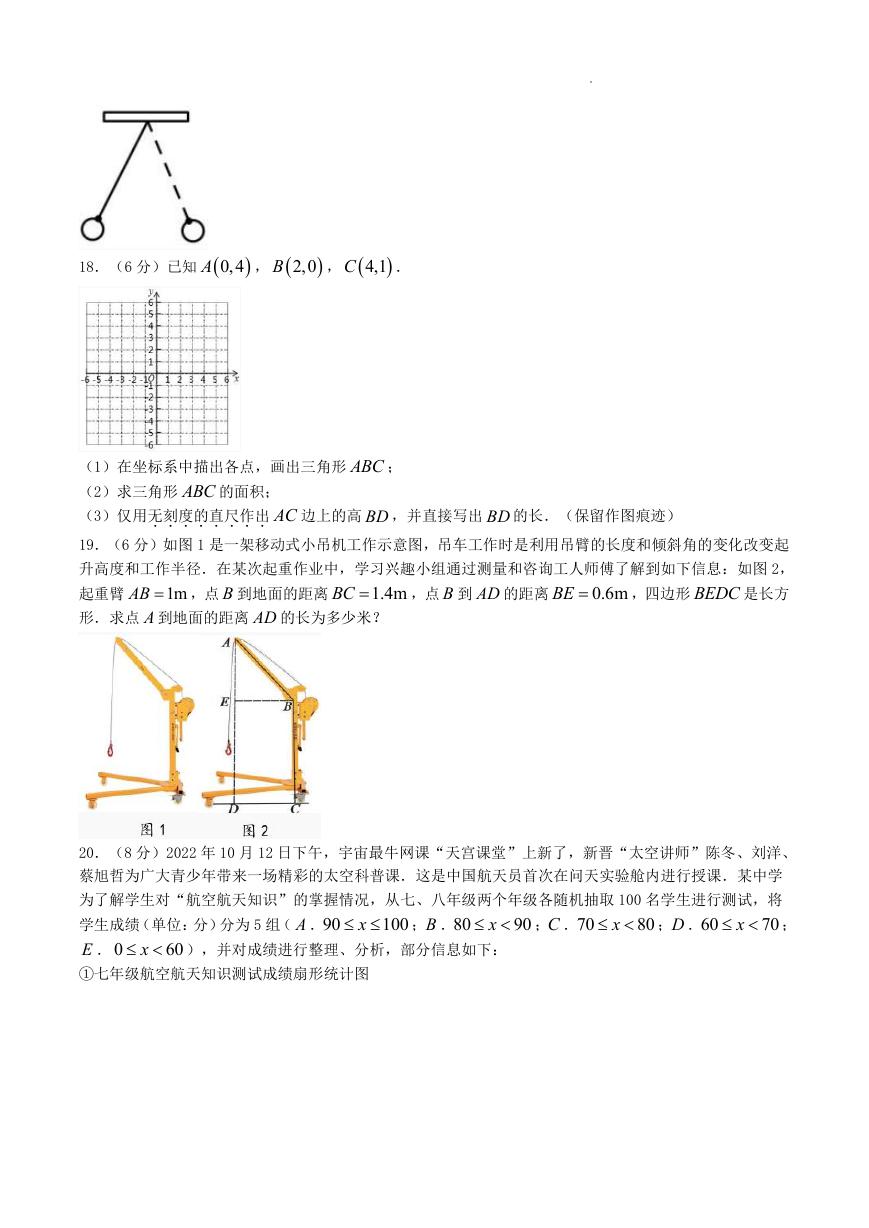
    的比例计算综合成绩（百分制，单位：分）．已知该老师的各项成绩分别是：演讲内容 86 分、语言表达 92 分、神情动作 90 分、仪表形象 88 分，则该老师最后的成绩是______． 14．在我国古算书《周髀算经》中早有记载，如图 1，以直角三角形的各边为边分别向外作正方形，再把较 S  ，则图中阴影部分的面 小的两张正方形纸片按如图 2 的方式放置在最大的正方形内，若 1 积是______． 36 S  ， 2 64 15．如图，一张长方形纸片 ABCD ， EF ，再将 ABM△ AB  ， 4 AD  ．先对折长方形纸片使 AB 与CD 重合，得到折痕 6 沿 AM 折叠，当点 B 恰好落在折痕 EF 上时，则 BM 的长为______． 三、解答题（本大题共 8 个小题，共 70 分） 16．（12 分）计算下列各式： （1）  1.6  40  （2） 8  3  （3） 6 2 15  （4） 4 2 3 6  2 18 3     2 5 ； ； 3 6  1 2 ； 2 3 1  ． 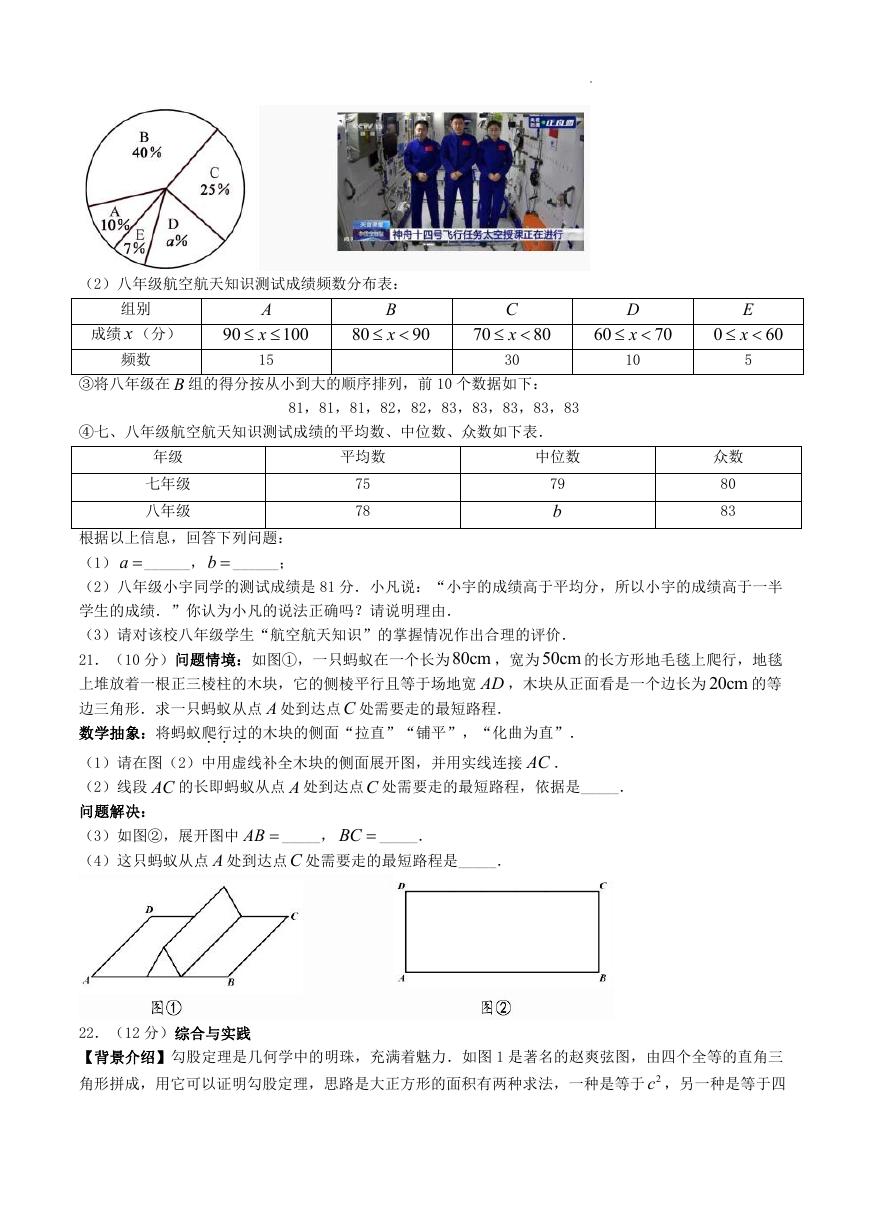17．（4 分）如图，一根细线上端固定，下端系一个小重物，让这个小重物来回自由摆动，来回摆动一次所 用的时间t （单位：s ）与细线的长度l （单位：m ）之间满足关系 2π t  小重物来回摆动一次所用的时间是多少？（ π 3.14  ，结果精确到 0.1） l 10 ．当细线的长度为0.4m 时， 学科 网（北 京）股 份有限 公司
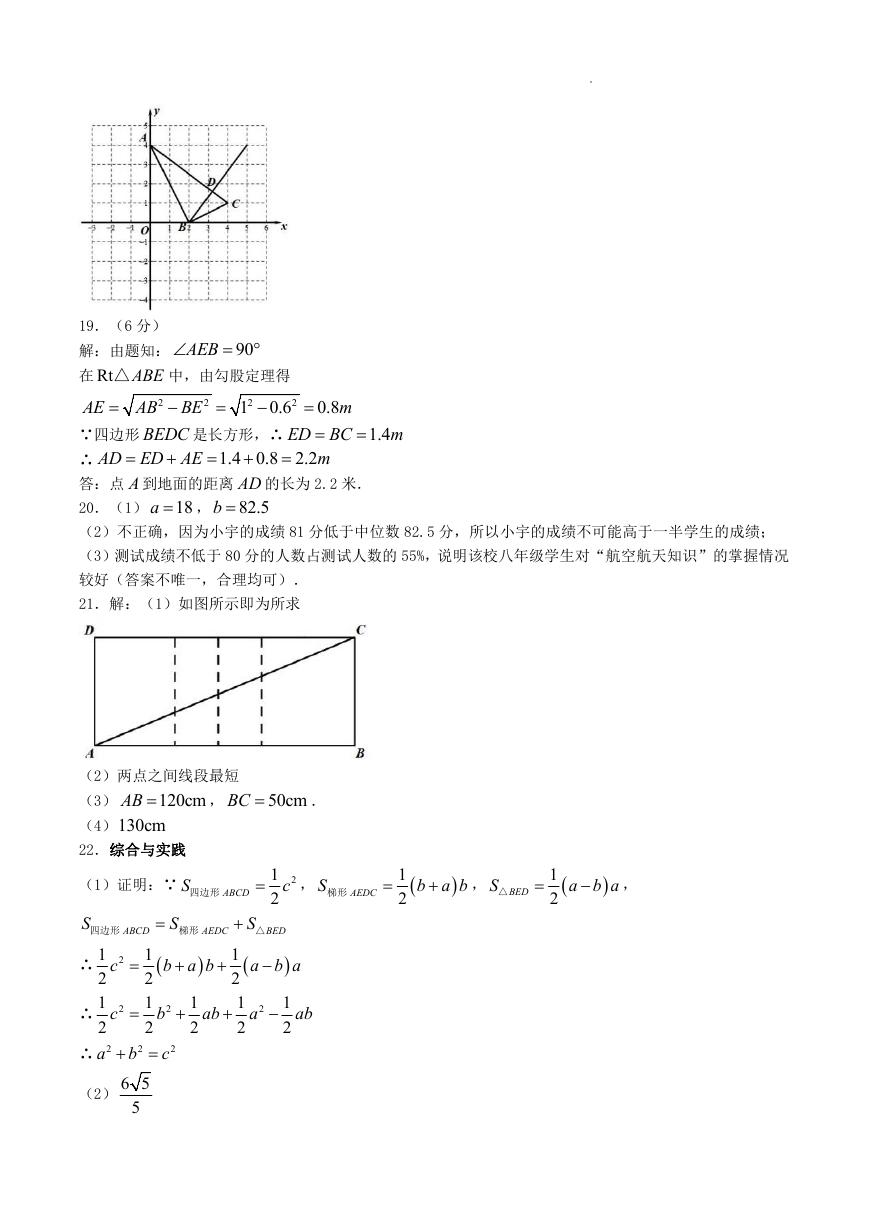
    18．（6 分）已知  A 0,4 ，  B 2,0 ，  4,1C ． （1）在坐标系中描出各点，画出三角形 ABC ； （2）求三角形 ABC 的面积； （3）仅用无刻度的直尺作出 ．．．．．．．．AC 边上的高 BD ，并直接写出 BD 的长．（保留作图痕迹） 19．（6 分）如图 1 是一架移动式小吊机工作示意图，吊车工作时是利用吊臂的长度和倾斜角的变化改变起 升高度和工作半径．在某次起重作业中，学习兴趣小组通过测量和咨询工人师傅了解到如下信息：如图 2， ，四边形 BEDC 是长方 AB  ，点 B 到地面的距离 ，点 B 到 AD 的距离 BC  0.6m 1.4m BE  1m 起重臂 形．求点 A 到地面的距离 AD 的长为多少米？ 20．（8 分）2022 年 10 月 12 日下午，宇宙最牛网课“天宫课堂”上新了，新晋“太空讲师”陈冬、刘洋、 蔡旭哲为广大青少年带来一场精彩的太空科普课．这是中国航天员首次在问天实验舱内进行授课．某中学 为了解学生对“航空航天知识”的掌握情况，从七、八年级两个年级各随机抽取 100 名学生进行测试，将 学生成绩（单位：分）分为 5 组（ A ．90 70 E ． 0 ①七年级航空航天知识测试成绩扇形统计图 x  ），并对成绩进行整理、分析，部分信息如下： x  ；D ．60 x  ；C ．70 ；B ．80 x  100 x  ； 90 60 80 学科 网（北 京）股 份有限 公司
    （2）八年级航空航天知识测试成绩频数分布表： B 组别 100 80 x  90 70 成绩 x （分） 90 频数 A x  15 C x  30 80 60 D x  10 70 0 E x  5 60 ③将八年级在 B 组的得分按从小到大的顺序排列，前 10 个数据如下： 81，81，81，82，82，83，83，83，83，83 ④七、八年级航空航天知识测试成绩的平均数、中位数、众数如下表． 年级 七年级 八年级 平均数 75 78 中位数 79 b 众数 80 83 根据以上信息，回答下列问题： （1） a  ______，b  ______； （2）八年级小宇同学的测试成绩是 81 分．小凡说：“小宇的成绩高于平均分，所以小宇的成绩高于一半 学生的成绩．”你认为小凡的说法正确吗？请说明理由． （3）请对该校八年级学生“航空航天知识”的掌握情况作出合理的评价． 21．（10 分）问题情境：如图①，一只蚂蚁在一个长为80cm ，宽为50cm 的长方形地毛毯上爬行，地毯 上堆放着一根正三棱柱的木块，它的侧棱平行且等于场地宽 AD ，木块从正面看是一个边长为 20cm 的等 边三角形．求一只蚂蚁从点 A 处到达点C 处需要走的最短路程． 数学抽象：将蚂蚁爬行过．．．的木块的侧面“拉直”“铺平”，“化曲为直”． （1）请在图（2）中用虚线补全木块的侧面展开图，并用实线连接 AC ． （2）线段 AC 的长即蚂蚁从点 A 处到达点C 处需要走的最短路程，依据是_____． 问题解决： （3）如图②，展开图中 AB  _____， BC  _____． （4）这只蚂蚁从点 A 处到达点C 处需要走的最短路程是_____． 22．（12 分）综合与实践 【背景介绍】勾股定理是几何学中的明珠，充满着魅力．如图 1 是著名的赵爽弦图，由四个全等的直角三 角形拼成，用它可以证明勾股定理，思路是大正方形的面积有两种求法，一种是等于 2c ，另一种是等于四 学科 网（北 京）股 份有限 公司
    个直角三角形与一个小正方形的面积之和，即 ab   4  1 2 b a  ，从而得到等式 2 2 c  1 2 ab   4  b a  ， 2 化简便得结论 2 a 求法”．  2 b  ．这里用两种求法来表示同一个量从而得到等式或方程的方法，我们称之为“双 2 c  90   BAC   DEA 和 DEA△ 如图 2 放置，其三边 ，显然 BC AD 【方法运用】千百年来，人们对勾股定理的证明趋之若鹜，其中有著名的数学家，也有业余数学爱好者．向 常春在 2010 年构造发现了一个新的证法：把两个全等的直角三角形 ABC△ 长分别为 a ，b ， c ， （1）请用 a ，b ，c 分别表示出四边形 ABDC ，梯形 AEDC ， EBD△ 之间的关系，证明勾股定理 2 a 【方法迁移】请利用“双求法”解决下面的问题： （2）如图 3，小正方形边长为 1，连接小正方形的三个顶点，可得 ABC△ AC  ， （3）如图 4，在 ABC△ 23．（12 分）综合与探究 如图，在平面直角坐标系中，已知  一象限内的点， ，则 AB 边上的高为______． BC  ，设 BD x ，求 x 的值． 中， AD 是 BC 边上的高， B b ，其中 a ，b 满足 的面积，再探究这三个图形面积 0,A  ， AB BC  ，点C 是第 0 a ，  AB  ， 4 ABC a   2 2  ． c ,0  b  2 1  90  2 b ． ． 5 6 （1）分别求出点 A 、 B 、C 的坐标． （2）如果在第二象限内有一点  ,1 请求出点 P 的坐标；若不存在，说明理由． （3）在平面直角坐标系是否存在点 E ，使 ABE△ 不存在，请说明理由． P m ，是否存在点 P ，使得 ABP△ 的面积等于 ABC△ 的面积？若存在， 与 ABC△ 全等，若存在，请直接写出点 E 的坐标；若 命题人：王凤 审题人：王巧娟 学科 网（北 京）股 份有限 公司
    一、选择题（每小题 3 分，共 30 分） 八年级数学试题答案 题号 答案 1 B 2 B 3 D 4 D 5 D 6 A 7 C 8 D 9 D 10 D 二、填空题（每小题 3 分，共 15 分） 11．212． 1, 3   13．89.4  14．16 15． 16 4 7  3 三、解答题（共 70 分） 16．（共 12 分）计算下列各式： （1）  1.6  40  （2） 8  3  （3） 6 2 15  （4） 4 2 3 6  2 18 3     2 5   2 10 5  2 10  10 5  9 10 5 ；  2 6  6  ； 6 3 6  2  3 1  1 2  3 2 6 5 3 2     6 5 ；   4 3 3   3 2 3 1      4 3 3 4 2 3     ． 3 17．解：当 0.4 l  时， t  2π 0.4 10  0.4π 1.3  答：小重物来回摆动一次所用的时间是1.3s ． 18．解：（1）如图所示的三角形 ABC 即为所求． （2）方法 1： S △ ABC             4 3 16 4 1 6 5     4 4 4 2 1 2 1 2 1 2 AB   ，∴ ABC△ 2 2 1 2  ， 2 4 BC  是直角三角形， 20 2 2 2  2 1  ， 2 AC  5 2 3  2 4  25 方法 2：由勾股定理得 2 ∴ 2 AB AC 2 2 S △ ABC  5  5  BC  1 2 5   2 （3）如图所示的线段 BD 即所求作的高， BD 的长为 2． 学科 网（北 京）股 份有限 公司
    19．（6 分） 2 2      2 1 90  BE AEB 解：由题知： 在 Rt ABE△ 中，由勾股定理得 2 0.6 m AE AB ∵四边形 BEDC 是长方形，∴ ED BC  ∴ 答：点 A 到地面的距离 AD 的长为 2.2 米． 20．（1） 18 （2）不正确，因为小宇的成绩 81 分低于中位数 82.5 分，所以小宇的成绩不可能高于一半学生的成绩； 0.8  1.4 0.8 2.2 m a  ， 82.5 AD ED AE b  1.4 m       （3）测试成绩不低于 80 分的人数占测试人数的 55%，说明该校八年级学生对“航空航天知识”的掌握情况 较好（答案不唯一，合理均可）． 21．解：（1）如图所示即为所求 （2）两点之间线段最短 ， BC  50cm ． 120cm AB  （3） （4）130cm 22．综合与实践 （1）证明：∵ S 四边形   ABCD 1 c 2 2 ， S 梯形   AEDC  1 2   b a b  ， S △  BED   a b a  ， 1 2  S 梯形   AEDC   b   b a b 1 2  2 ab  BED S  △ 1  2 1 2 a   a b a 1 2  2 ab S   ∴ 四边形 ∴ 2 c   ABCD 21 1 c 2 2 1 1 2 2 ∴ 2 a b  （2） 6 5 5  2 2 c 学科 网（北 京）股 份有限 公司
    分享到：
    赞 收藏

    相关推荐

    资料库

    初中二年级

    共收录369份资料，累计95个分类，关注成员有19位，主要包括：2021年,2020年,黑龙江,2022年,贵州,内蒙古,云南,青海,吉林,上海,甘肃,浙江,海南,四川,湖南,广西,山西,山东,辽宁,福建,湖北,河南,河北,江西,广东,安徽,天津,陕西,北京,2019年,江苏

    热门标签

    2021年 2020年 黑龙江 2022年 贵州 内蒙古 云南 青海 吉林 上海 甘肃 浙江 海南 四川 湖南 广西 山西 山东 辽宁 福建 湖北 河南 河北 江西 广东 安徽 天津 陕西 北京 2019年 江苏

    最新资料