Vol.29 No.11 2009.11 船电技术 2009 年 第 11 期 双馈风力发电机 P—Q 解耦控制的研究 林波 方宁 刘红兵 （湖南铁道职业技术学院电气工程系, 湖南 412001） 摘 要: 介绍了一种定子磁场定向的双馈风力发电机矢量控制系统，给出了双馈电机在两相同步旋转坐标 系下的数学模型。利用定子磁场定向的矢量控制方法将同步坐标系下的双馈电机模型简化后获得了矢量控 制系统的模型，建立了基于 Matlab/Simulink 的仿真平台，验证了定子磁场定向矢量控制可以实现双馈风力 发电机有功功率、无功功率的独立解耦控制。 关键词：双馈电机 矢量控制 解耦 风力发电 中图分类号：TM315 文献标识码：A 文章编号：1003-4862 (2009)11-0043-05 P—Q Decoupled Control Research for Doubly-fed Wind Power Generator Lin Bo，Fang Ning，Liu Hongbing (Department of Electrical Engineering , Hunan Railway Polytechnic, Hunan 412001, China) Abstract: In this paper, it is presented that a stator flux-oriented vector control system of the doubly-fed wind power generator. And it is built that the mathematic model of two phase synchronous rotating co-ordinate for the doubly-fed machine. The model of vector controlling system is obtained after that the doubly-fed machine is simplified by the vector control strategy of stator flux-oriented vector control, and the simulation platform, which is base on MATLAB/SIMULINK, is established. It can be concluded that the stator flux-oriented vector control strategy can control active and reactive power of Doubly-Fed Wind Power Generator decoupled respectively． Key words: doubly-fed Machine; vector control; decoupling; wind power generation 1 引言 双馈电机采用交流电源励磁，其可调量有三 个，而通过励磁调节不仅保持了同步电机可以调 到和直流电机一样的控制性能[4]。 本文介绍了一种定子磁场定向的双馈电机矢 量控制系统，建立了基于 Matlab/Simulink 双馈风 力发电机系统的仿真平台，对定子磁场定向矢量 节无功功率的优点，还能调速、调有功功率，因 控制策略进行了仿真研究，验证了此控制方法可 而在抽水蓄能及风力发电等方面具有广阔的应用 前景[1~3]。矢量控制技术是交流传动调速系统实 现解耦控制的核心，它通过电机统一理论和坐标 变换理论，把交流电机的定子电流分解成磁场定 向旋转坐标系的励磁电流分量和与之相垂直的转 矩分量，然后分别对它们进行控制使交流电机得 实现双馈电机有功功率和无功功率的快速、解耦 控制。 2 双馈电机的基本方程 由于电机转子的旋转运动，使得定、转子间 的互感为定、转子相对位置角 θr 的余弦函数，描 收稿日期: 2009-06-12 作者简介：林波（1983—），男，讲师，主要研究方向：自动化与新能源。 43 

船电技术 2009 年 第 11 期 Vol.29 No.11 2009.11 述电机特性的数学模型是一组非线性、时变系数 的微分方程组，如将其变换到在空间以同步速ω1 旋转的 d－q 坐标系，则当 A、B、C 坐标系中的 变量为正弦函数时，d、q 坐标系中的变量为直流。 这样，双馈电机的非线性、时变系数微分方程组 在 d－q 同步坐标系中变成了常系数微分方程组。 规定定子绕组按发动机惯例，转子绕组按电动机 惯例，可得双馈电机在 d－q 同步旋转坐标系下的 基本方程如下[5]。 定子电压方程： ωψ qs 1 + ψ ds (1) ωω ψ qs + ds 1 d dt d dt ds − = − r i s ds ⎧ u ⎪⎪ ⎨ ⎪ u ⎪⎩ 转子电压方程： r i s qs = − + qs 3 定子磁场定向的矢量控制策略[6][7] 由于双馈风力发电机系统是一个高阶次、非 线性、强耦合的多变量系统，若用常规的控制方 法将十分复杂，而且效果难以令人满意，而矢量 控制可以在坐标变换的基础上，简化电机内部各 变量间的耦合关系。 双 馈 电 机 的 定 子 绕 组 直 接 接 在 无 穷 大 电 网 上，可以近似地认为定子的电压幅值、频率都是 恒定的，所以选择定子电压或定子磁场定向方式， 使定子磁链矢量与 d 轴重合，定子电压矢量与 q 轴同向。本节将对定子磁场定向方式下的矢量控 制策略进行研究。 如 1 图所示，当选定定子磁场矢量 ψs 的方向 为 d-q-0 坐标系轴 d 方向后，有： 0 sψ ψ= ； qsψ = ； u dsu = ； qs 0 ds U= 。 s ⎧ u ⎪⎪ ⎨ ⎪ u ⎪⎩ = r i r dr − dr = r i r qr + qr ( ω ω ψ qr − ) 1 r ( ω ω ψ dr − ) 1 r 定子磁链方程： = − = − L i s ds L i s qs ψ ⎧⎪ ds ⎨ ψ ⎪⎩ qs 转子磁链方程 + + L i m dr L i m qr + + d dt d dt ψ dr ψ qr (2) q su d rω a 1ω sψ ϕ rθ A (3) 图 1 空间矢量示意图 忽略定子绕组电阻 rs，此时定子电压方程 为： ψ ⎧⎪ dr ⎨ ψ ⎪⎩ qr = − = − L i m ds L i m qs + + L i r dr L i r qr 运动方程： (4) = ⎧ T ⎪ m ⎨ ⎪ = T ⎩ e T e + dJ n ( ω m dt − p n L i i p m qs dr i i ds qr ) = n p ( ψ ψ i ds qs − i qs ds ) 定子输出功率方程 (5) = = u i + qs qs u i − ds qs P u i ds ds 1 Q u i qs ds 1 (6) ⎧⎪ ⎨ ⎪⎩ 以上各式中，下标带 s 的为定子侧向量，下 标带 r 的为转子侧折算到定子侧的向量， Lm 为 互感。 44 s ⎧ U ⎪⎪ ⎨ ⎪ = − 0 ⎪⎩ = − r i s qs + ωψ ds 1 ψ ωψ s = qs 1 r i s ds − ωψ qs 1 + ψ ds = d dt ψ s + d dt d dt (7) 将 uds=0，uqs=Us 代入定子输出功率方程，有 P U i =⎧⎪ s qs 1 ⎨ Q U i = ⎪⎩ s ds 1 (8) 由式(8)可知，在定子磁场定向下，双馈电机 定子输出有功功率 P1 和无功功率 Q1 分别与定子 电流在 d、q 轴上的分量 iqs、ids 成正比，调节 iqs、 ids 可分别独立地调节 P1、Q1，实现两者的解耦控 制。 将 ψds=ψs，ψqs=0 代入定子磁链方程，整理后 有： 

Vol.29 No.11 2009.11 船电技术 2009 年 第 11 期 (9) 则有： u qr = a ( ω ω ψ ω ω r − + − b ) ( 1 1 r s i ) dr 。 ⎧ i ⎪⎪ dr ⎨ ⎪ i qr ⎪⎩ = = L s L m L s L m i ds + ψ s L m i qs 将式(9)中 ids 用 idr 表示，iqs 用 iqr 表示，代入 转子磁链方程，整理后有： + bi dr a ψ ψ ⎧⎪ s dr ⎨ bi ψ ⎪⎩ qr qr = = (10) 其中： a = ， L m L s b L r = (1 − L 2 )m L L s r 。 再将式(10)代入转子电压方程，整理后有： ⎧ u ⎪⎪ ⎨ ⎪ u ⎪⎩ = ( r r + b dr = ( r r + b qr d dt d dt i ) dr − b ( ω ω r − 1 i ) qr i ) qr + a ( ω ω ψ ω ω r − + − b ) ( 1 1 r s i ) dr (11) 同 时 令 u ' dr = ( r r + b u dr b = − iω ω 1( ) qr − r u ， ' qr = ( r r + d dt b i ) dr d dt i ) qr ， ， u u ⎧ ⎪ ⎨ ⎪⎩ dr qr = = u u ' dr ' qr + + u u dr qr (12) dru 、 ' 式中， ' qru 为实现转子电压、电流解耦 控制的解耦项； dru 、 qru 为消除 d、q 轴转子 电压、电流分量间交叉耦合的补偿项。将转子电 压分解为解耦项和补偿项后，既简化了控制，又 能保证 控制 的精度 和动 态响应 的快 速性。 有了 C → 坐标变换，这个转子三 dru 、 qru 后，通过 2 相电压分量值就可以用作调制波去产生转子侧励 3 r s 磁变频器所需的指令信号，用于控制逆变主电路 开关管的通断，以产生所需频率、大小、相位的 三相交流励磁电源。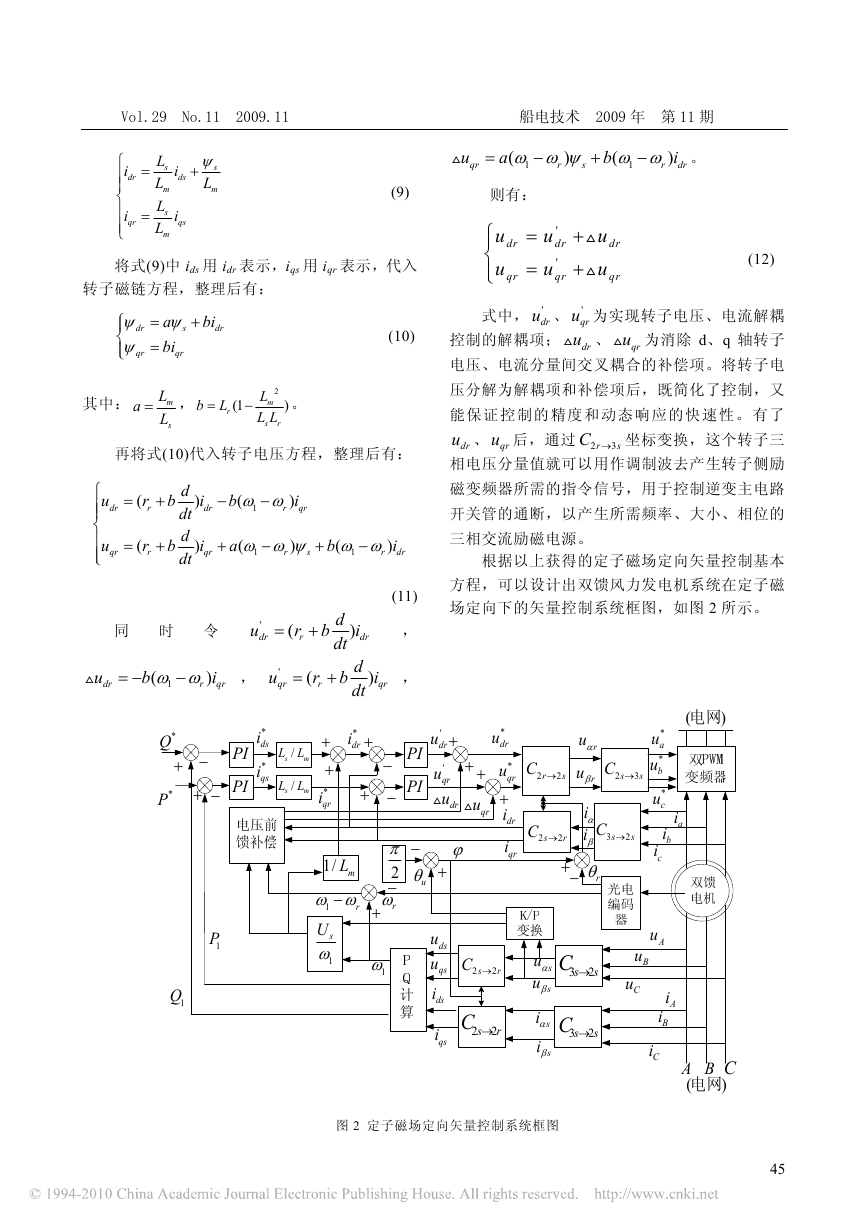 根据以上获得的定子磁场定向矢量控制基本 方程，可以设计出双馈风力发电机系统在定子磁 场定向下的矢量控制系统框图，如图 2 所示。 *Q + *P − + − dsi * qsi * PI PI L L /s m L L /s m + + qri * dri + * − − + PI PI dru ' + qru ' dru + + qru − uθ ϕ + 1/ mL rω ω− 1 sU ω 1 π 2 − + rω 1ω 1P 1Q dru * qru * + dri qri ruα ruβ C → s 2 3 s C → r 2 2 s C → s 2 2 r iα C → iβ s 3 +− rθ 2 s ( )电网 au * bu * cu * bi ci ai dsu qsu dsi qsi C → s 2 2 r rC → 2s 2 sC → 2s 3 sC → 2s 3 suα suβ siα siβ Bu Cu Au Ai Bi Ci 图 2 定子磁场定向矢量控制系统框图 A B C ( )电网 45 

船电技术 2009 年 第 11 期 Vol.29 No.11 2009.11 由控制框图图 2 可知，此控制系统外环为功 率控制环，内环为电流控制环。在功率外环控制 环中，有功功率指令值 P*根据风力机最佳转速给 出，无功功率指令值 Q*根据电网需求给定。反馈 功率则是通过对发电机定子侧输出电压、电流的 检测再经过坐标变换后按式(8)计算求得。有功功 率、无功功率指令与反馈值相比较，经过 PI 调节 qsi 及 器，分别输出发电机定子电流有功分量指令 * dsi ，根据式(9)可获得转子电流参考 无功分量指令 * dri ，将它们分别与转子电流反馈值 qri 分量 * 和 dri 相比较，并经过 PI 调节后，可输出转子电 dru ，再加上转子电压补偿项 qru 、 压解耦项 ' dru 就可以获得转子电压指令值 * dru 。经过 矢量坐标变换后，最终可获得转子侧 PWM 交流 bru 、 励磁电源所需要的三相电压控制指令 * aru 、 * qru 、 * qru 和 ' qri 和 * cru 。 * 5 双馈风力发电机系统的仿真研究 由控制框图 2 可在 MATLAB/SIMULINK 中 建立双馈风力发电机系统仿真模型，如图 3 所示， 各模块的仿真功能在图中已经标出。本文仿真所 用 交 流 励 磁 发 电 机 的 参 数 为 ： 额 定 功 率 Pn=2.5kW ， 额 定 电 压 Un=220V ， 额 定 频 率 f1=60Hz，极对数 np=2，定子绕组电阻 rs=0.436Ω， 转 子 绕 组 电 阻 rr=0.818Ω ， 定 子 绕 组 漏 感 Lls=2mH ， 转 子 绕 组 漏 感 Llr=2mH ， 互 感 Lm=70.32mH，转动惯量 J=0.088kg·m2。所用风力 机仿真参数为：风轮半径 R=3m，最佳叶尖速比 λopt=9.8，最大风能利用系数 Cpmax=0.4，齿轮传动 比 N=8。 风速 V Tm wm Pmax 风机 uas ubs ucs Qref 无功参考值 三相电源 Pmax Pref s Qref Pref in urref 有功参考值 矢量控制 Tm uas ubs ucs uar ubr ucr out uas ubs ucs ur uar ubr ucr 变频器 交流励磁电机 图 3 双馈风力发电机系统定子磁场定向矢量控制仿真模型 4.1 定子有功功率的独立调节过程 假设系统稳定运行在风速 V1=6m/s 下，并已 经实现 最大 风能捕 获。 在 t1=5s 时风速突 变为 V2=7m/s，参考无功功率保持为 150Var 不变。定 子有功、无功功率的调节过程如图 4 所示。 250 200 150 100 50 / r a V 率 功 4 5 6 7 8 9 10 11 时间/s （b）无功输出 1300 1200 1100 1000 / W 率 功 900 46 4 5 6 7 8 9 10 11 时间/s （a）有功输出 图 4 风速变化时，定子有功功率、无功功率的调节过程 由于风速变大，风力机吸收的能量会增大， 图 4(a)显示出发电机的实际有功功率输出能很好 地跟踪风速的变化。从图 4(b)可以看出，在有功 

Vol.29 No.11 2009.11 船电技术 2009 年 第 11 期 功率的调节过程中，系统的无功功率恒等于参考 定子输出的有功功率不发生变化，无功功率也很 无功输入，没有发生变化，这说明有功功率的调 节不影响无功功率。 4.2 定子无功功率的独立调节过程 假定风速保持 V1=6m/s 不变，系统稳定运行。 给定无功功率参考值 Qref 在 t1=5s 时由 150Var 变 为 0，定子有功、无功功率的调节过程如图 5 所 示。 1000 W / 率 功 950 900 850 800 4 5 6 7 8 9 10 11 时间/s （a）有功输出 300 200 100 0 r a V / 率 功 -100 4 5 6 7 时间/s 8 9 10 11 （b）无功输出 图 5 给定无功功率变化时，定子有 功、无功功率的调节过程 由图 5(b)可以看出，独立调节无功功率时， 双馈电机的输出无功功率较好地跟踪了给定值， 同时，其有功功率输出没有发生变化。这说明无 功功率的调节过程不影响有功功率。 5 结束语 本文阐述了双馈风力发电机系统矢量控制 的基本原理，推导出了定子磁场定向矢量控制的 控制策略。利用Matlab/Simulink软件工具建立了 风力机、双馈电机和矢量控制系统的仿真模型并 进行了仿真，仿真结果表明：当风速发生阶跃变 化时，双馈电机定子输出的无功功率保持不变， 同时双馈电机的有功功率很快进入了新的稳定状 态；而当给定的参考无功功率变化时，双馈电机 快进入了新的稳定状态，即验证了定子磁场定向 矢量控制的正确性。 参考文献: [1] 伍小杰，柴建云，王祥珩. 变速恒频双馈风力发电系 统交流励磁综述[J].电力系统自动化，2004, 28(23): 92-96. [2] R. Pena. J. C. Clare. and G M. Asher. Doubly Fed Induction Generator Using Back-to-back PWM Converters and Its Application to Variable Speed Wind-energy Generation[J]. IEEE Proc.B, vol 143. no. 3 ,May 2002: 231-241. [3] Daniel J. Trudnowski, Andrew Gentile, Jawad M. Khan,and Eric M. Petritz. Fixed-speed Wind-generator and Wind-park Modeling for Transient Stability Studies. IEEE Transaction On Power Systems, Vol. 19, No. 4, November 2004 pp1911-1917. [4] 陈伯时，陈敏逊． 交流调速系统[M]．北京：机械工 业出版社，1998. [5] 刘其辉. 变速恒频风力发电系统运行与控制研究[D]. 浙江：浙江大学，2005. [6] 刘其辉，贺益康，张建华. 交流励磁变速恒频风力发 电机的运行控制及建模仿真[J].中国电机工程学报, 2006，26（5）：43-50. [7] 刘其辉，贺益康，赵仁德. 交流励磁变速恒频风力发 电 系统 的 运 行 与 控制[J].电 工 技 术 学 报 ，2008，23 （1）：129-136. [8] 吴国祥，黄建明，陈国呈，蔚兰，俞俊杰. 变速恒频 双馈风力发电运行综合控制策略[J]. 电机与控制学 报, 2008,12（4）：435-441. [9] 马幼捷，尹向前，周雪松，张继东. 变速恒频双馈风 电机组的控制策略研究[J].电气传动，2008，38（4）： 12-16. Power [10] Eftichios Koutroulis, Kostas Kalaitzakis. Design of a Maxi-mum for Wind-energy-conversion IEEE Transactions on Industrial Electronics, 2006, 53 (2) :486-494 . Ap-plications. Tracking System 47