书书书doi:10．3969/j．issn．1009－3230．2015．01．001基于Matlab/Simulink的光伏电池输出特性仿真研究唐俊1，2，周海峰1，2，王荣杰1，2，叶晓军1，2(1．集美大学轮机工程学院，福建厦门361021;2．福建省船舶与海洋工程重点实验室，福建厦门361021)摘要:在清洁能源飞速发展的今天，以太阳能为首的清洁能源已经成为了国内外研究的热点。本文采用Matlab/Simulink仿真模块，建立一种以太阳能光伏电池基本参数为基础的光伏电池数学模型，利用该模型能模拟在不同的太阳辐照度和工作温度下不同光伏模块的光伏电池P－U与I－U输出特性，仿真结果验证了此模型的准确性。关键词:光伏电池;数学模型;Matlab仿真中图分类号:TP391．9文献标志码:A文章编号:1009－3230(2015)01－0001－05ＲesearchonCharacteristicsofPhotovoltaicCellsBasedonMatlab/SimulinkTANGJun1，2，ZHOUHai－feng1，2，WANGＲong－jie1，2，YEXiao－jun1，2(1．MarineEngineeringInstituteofJimeiUniversityXiamen361021;2．ProvincialKeyLaboratoryofNavalArchitecture＆OceanEngineering，Xiamen361021，China)Abstract:Withthefastdevelopmentofcleanenergy，solarledcleanenergyhavebeenpaidmoreattentionbydomesticandinternational，Inthispaper，establishmentofaphotovoltaiccelloutputcharacteristicsbasedonsolarphotovoltaicarraymoduleparametersThemodelcansimulationanysolarradiationintensity，ambienttemperatureoutputcharacteristics．ThesimulationresultsverifythedesignaccuracyofPhotovoltaicmodel．Keywords:PhotovoltaicCells;Mathematicalmodel;MatlabSimulink0引言收稿日期:2014－10－15修订日期:2014－12－20作者简介:唐俊(1990－)，男，硕士研究生，主要研究方向为清洁能源的利用。基金项目:国家自然科学基金资助项目(51179074、51309116);四川省智能重点实验室开放课题(201312270005);李尚大基金(ZC2013012)集美大学博士启动金(ZQ2013001、ZQ2013007);产学研项目(S13060)进入21世纪，全球经济增长引发的能源消耗达到了前所未有的程度。常规化石燃料能源不仅越来越满足不了人类社会发展，而且因化石燃料的过度消耗引起的全球变暖以及生态环境恶化给人类带来了更大的生存威胁，能源和环境的可持续发展已成为人类最为关注的重大问题之一。同时由于，太阳能光伏发电具有最理想的可持续发展特征:最丰富的资源和最清洁的发电过程;目前太阳能光伏发电成为世界可再生能源发展的一大方向;光伏电池的输出特性不仅与本身模块的内部参数有关，而且还随着外界温度和光照的改变而实时变化［1］，文中通过分析光伏模块的直流物理模型，应用Matlab/Simulink仿真软件研究设计了一种光伏电池的通用模型，该模型在给定的光伏模块参数，如标准条件下光伏电池的开路电压Uoc、短路电流Isc、最大功率点电压Um、最大功率点电流Im下，改变太阳辐射强度和工作温度，考12015年第1期(总第205期)应用能源技术

虑其对光伏输出特性的影响。仿真研究结果表明，该简化光伏电池数学模型简单，且具有较高的准确性。1光伏电池等效电路和数学模型太阳电池是一种将光能直接转化成电能的半导体器件，它的基本构造是由半导体的P－N结组成。基本特性与二极管类似，其等效电路由产生光生电流的恒流源及一系列电阻(内部并联电阻Ｒsh和串联电阻Ｒs)组成［2－3］，一类是串联电阻，另一类是并联电阻(又称旁路电阻)，前者主要是由由于半导体材料的体电阻、金属电极与半导体材料的接触电阻、扩散层横向电阻以及金属电极本身的电阻四个部分产生的Ｒs;后者主要是由于电池表面污染、半导体晶体缺陷引起的边缘漏电或耗尽区内的复合电流等原因产生的旁路电阻Ｒsh。太阳能电池等效电路如图1所示［4］。图1光伏电池的等效电路由KCL(基尔霍夫电流定律)可得到公式:Iph－ID－Ish－I=0即I=Iph－ID－Ish。(1)式中:I为流过负载两端的工作电流;Iph为光生电流;ID为流过二极管P－N结的电流;Ish为流过并联电阻Ｒsh的电流。ID表达式为:ID=I0expqUDAKT－()1。(2)式中:I0为二极管反向饱和电流(A);K为玻耳兹曼常数，为1．38×10－23J/K;T为太阳能表面绝对温度(K);A为二极管的曲线因子，取值在1～2之间;q为电子电量;为1．6×10－19C。在旁路电阻Ｒsh两端的电压，因此流过旁路电阻Ｒsh的电流Ish为:Ish=U+IＲsＲsh。(3)式中:U为二极管输出电压(V);Ｒs为串联电阻Ｒs的阻值(Ω)。将式(2)、(3)代入式(1)，可得光伏电池输出的电流表达式为:I=Iph－I0expqUDAKT－()1－U+IＲsＲsh。(4)从公式(4)可知，光伏电池的串联电阻Ｒs越小，并联电阻Ｒsh越大，该太阳电池的性能越好，输出电流I越大。而实际上，Ｒs为低阻值，一般Ｒs的阻值通常小于1Ω，Ｒsh一般为几千欧［5］。同时根据KVL(基尔霍夫电压定律)，UD与输出电压U的关系:UD=U－IＲ。(5)这样就有Ish≈Isc，UD≈U，于是公式(4)可以化简为:I=Isc［1－C1(expUC2Uoc－1)］。(6)C1=1－ImI()scexp－UmC2Uoc。(7)C2=UmUoc－()1/ln1－ImI()sc。(8)式中:U、I为电池的输出电压和电流;C1、C2为修正系数。上述数学模型还与实际环境存在一定偏差，所以应该进行修正。忽略一些次要因素的影响，根据厂商提供的单晶硅太阳能电池作为参考。在环境条件改变时，如太阳辐射强度和工作温度变化，其性能也会相应发生变化，所以要对光伏电池的四个性能参数进行修正，得到接近实际的光伏电池模型，修正系数公式［6］:D1=SSref［1+a(T－Tref)］。(9)2应用能源技术2015年第1期(总第205期)

DU=［1－c(T－Tref)］ln［e+b(S－Sref)］。(10)I'sc=IscDII'm=ImD{I。(11)U＇oc=UocDUU＇m=UmD{U。(12)式中:Isc、Uoc、Im、Um为4个标准参考技术值;Sref为太阳光强参考值1000W/m2;Tref为电池参考温度值25℃;S、T为任意时刻太阳辐照度和电池工作温度;a和c为温度补偿系数，b为光强补偿系数，其中a=0．0025，b=0．0005，c=0.00288。［7］2光伏电池建模仿真下面运用Simulink对该光伏电池模型进行仿真［8－11］。从上面公式可知得到光伏电池实用仿真模型不需要复杂的参数，只需要四个基本性能参数即可模拟在不同辐照度和温度条件下的光伏电池输出特性。以式(6)为基础，根据公式(9)和公式(10)建立DI和DU子模块，将这两个子模块封装后，根据公式(11)和公式(12)建立修正后的Isc、Im、Uoc和Um子模块。图2为该模型的封装模块，并在内封装Isc、Uoc、Im、Um以及Sref、Tref参数。以DPL5M36－85为例，在标准条件下，即S=1kW/m2，T=25℃，AM=1．5的测试条件下4个技术参数:短路电流Isc=5．45A、开路电压Uoc=22．2V、最大功率点电流Im=4．95A和最大功率点电压Um=17．2V。参数设置图3所示。该封装模块输入实际的光照强度和温度，输出修正后的Isc、Uoc、Im和Um。图4为光伏电池模型内部结构。图2封装模块图3仿真电路参数设置图4电流输出模块32015年第1期(总第205期)应用能源技术

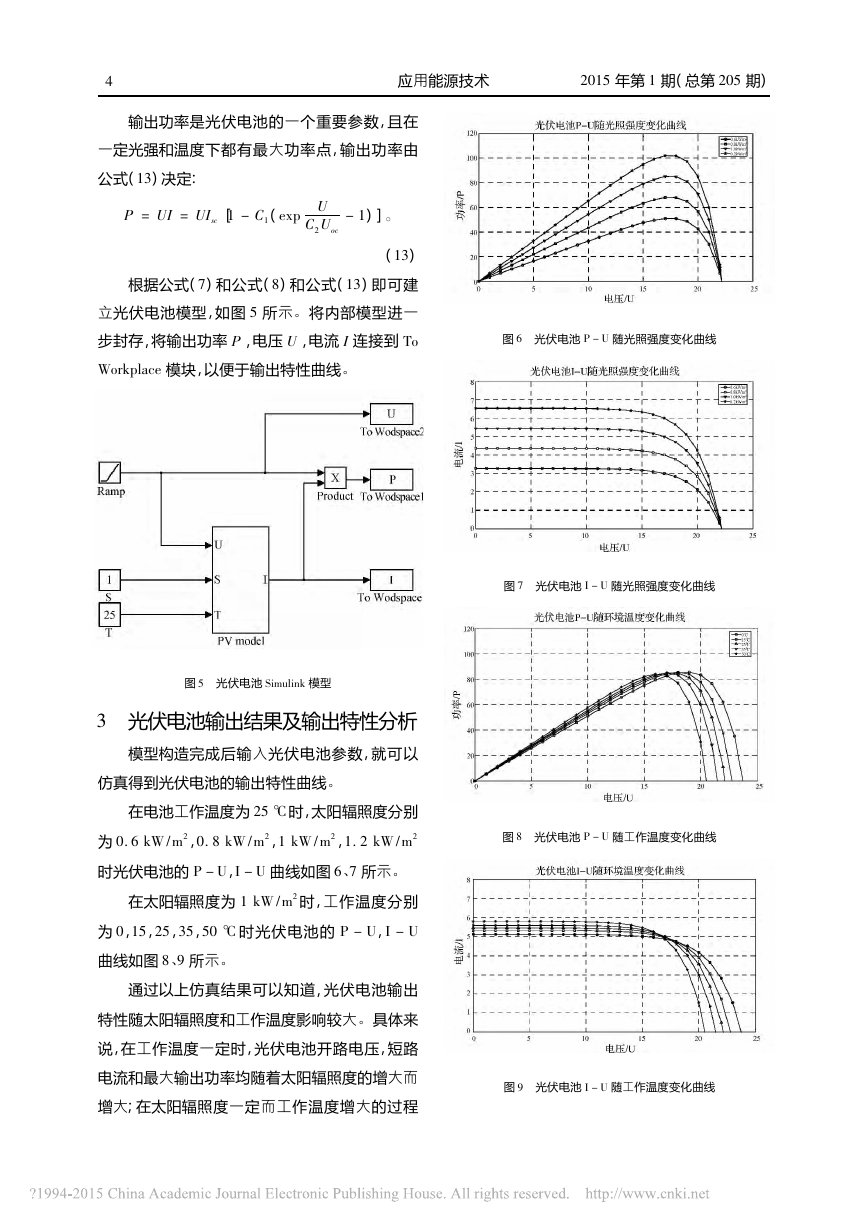
输出功率是光伏电池的一个重要参数，且在一定光强和温度下都有最大功率点，输出功率由公式(13)决定:P=UI=UIsc［1－C1(expUC2Uoc－1)］。(13)根据公式(7)和公式(8)和公式(13)即可建立光伏电池模型，如图5所示。将内部模型进一步封存，将输出功率P，电压U，电流I连接到ToWorkplace模块，以便于输出特性曲线。图5光伏电池Simulink模型3光伏电池输出结果及输出特性分析模型构造完成后输入光伏电池参数，就可以仿真得到光伏电池的输出特性曲线。在电池工作温度为25℃时，太阳辐照度分别为0．6kW/m2，0．8kW/m2，1kW/m2，1．2kW/m2时光伏电池的P－U，I－U曲线如图6、7所示。在太阳辐照度为1kW/m2时，工作温度分别为0，15，25，35，50℃时光伏电池的P－U，I－U曲线如图8、9所示。通过以上仿真结果可以知道，光伏电池输出特性随太阳辐照度和工作温度影响较大。具体来说，在工作温度一定时，光伏电池开路电压，短路电流和最大输出功率均随着太阳辐照度的增大而增大;在太阳辐照度一定而工作温度增大的过程图6光伏电池P－U随光照强度变化曲线图7光伏电池I－U随光照强度变化曲线图8光伏电池P－U随工作温度变化曲线图9光伏电池I－U随工作温度变化曲线4应用能源技术2015年第1期(总第205期)

中，光伏电池的开路电压减小，短路电流却逐渐增大，最大输出功率在减小。光伏电池的输出特性曲线具有非线性，而且有最大功率点，最大功率点随着太阳辐照度和工作温度的改变而改变。所以为了提高光伏电池的效率，一方面要使照射到光伏板上的太阳辐照度尽可能的大，尽量能够垂直于光伏电池板，另一方面需要采用最大功率点跟踪算法，理论上在一定的太阳辐照度和工作温度的条件下，伏安特性曲线上任何一点都是工作点，曲线上得到一点对应电流Im和电压Um的功率乘积最大，保证光伏电池工作一直在最大功率点附近，提高能量的转化效率。4结束语光伏电池的输出特性不仅与自身参数有关，还与太阳辐射度和电池工作温度有关。本文利用Matlab/Simulink建立模型，只需根据生产厂家提供的4个基本参数即可完成在不同太阳辐射度和工作温度下的光伏电池特输出性曲线，基本参数也可以在模块中更改，可以仿真不同型号的光伏电池。该模型结构简单，仿真结果与理想条件下的光伏电池输出特性曲线基本一致，为研究最大功率点的控制与太阳能光伏发电应用提供了便利的条件。参考文献［1］张建坡．光伏系统变步长最大功率跟踪策略仿真研究［J］．可再生能源，2009，27(5):10－14．［2］Huan－LiangTsai，Ci－SiangTu，Yi－JieSu．“De-velopmentofGeneralizedPhotovoltaicModelUsingMATLAB/SIMULINK”，ProceedingsoftheWorldCongressonEngineeringandComputerScienceWCECS，SanFrancisco，USA，2008．［3］KoutroulisE，KalaitzakisK，VoulgarisNC．Develop-mentofaMicrocontroller2Based，PhotovoltaicMaxi-mumPowerPointTrackingControlSystem［J］．IEEETransPowerElectronics，2001，16(1):46－54．［4］冯垛生．太阳能发电原理与应用［M］．北京:人民邮电出版社，2007:53－54．［5］杨金焕，于化丛，葛亮．太阳能光伏发电应用技术［M］．北京:电子工业出版社，2009:50－53．［6］符江升，肖大帅，杨钦超．基于Matlab/Simulink的光伏电池仿真模型研究［J］．电子元器件应用，2005，14(2):48－51．［7］陈玉鸣，张寅孩．基于MATLAB的光伏模块通用仿真模型［J］．工业控制计算机，2012，25(3):30－33．［8］王薇．MATLAB从基础到精通［M］．北京:电子工业出版社．［9］周德佳，赵争鸣．基于仿真模型的太阳能光伏电池阵列特性的分析［J］．清华大学学报，2007，47(7):1109－1112．［10］茆美琴，余世杰，苏建徽．带有MPPT功能的光伏阵列Matlab通用仿真模型［J］．系统仿真学报，2005，17(5):1248－1253．［11］TarakSalmi，MounirBouzguenda，AdelGastli，etal．MATLAB/SimulinkBasedModellingofSolarPhoto-voltaicCell［J］．INTEＲNATIONALJOUＲNALofＲENEWABLEENEＲGYＲESEAＲCH，2012，2(2):213－218．52015年第1期(总第205期)应用能源技术