第1页 / 共287页
第2页 / 共287页
第3页 / 共287页
第4页 / 共287页
第5页 / 共287页
第6页 / 共287页
第7页 / 共287页
第8页 / 共287页
MIT 单变量微积分lecture note+problem set+exam.pdf
18.01 Single Variable Calculus
Fall 2006
Lecture 1
18.01 Fall 2006
Unit 1: Derivatives
A. What is a derivative?
• G e o m e t r i c interpretation
• Ph}^sical interpretation
參 I m p o r t a n t for an}，m e a s u r e m e n t (economics, political science, finance, plxysics, etc.)
B. How to differentiate any function you know.
• For example:
d x 、
differentiate an}^ function is the subject of the first t w o w e e k s of this course.
arctana;^ \ye wn\ discuss w h a t a derivative is toda}^. Figuring out h o w to
■
Lecture 1: Derivatives, Slope, Velocity, and Rate
of Change
Geometric Viewpoint on Derivatives
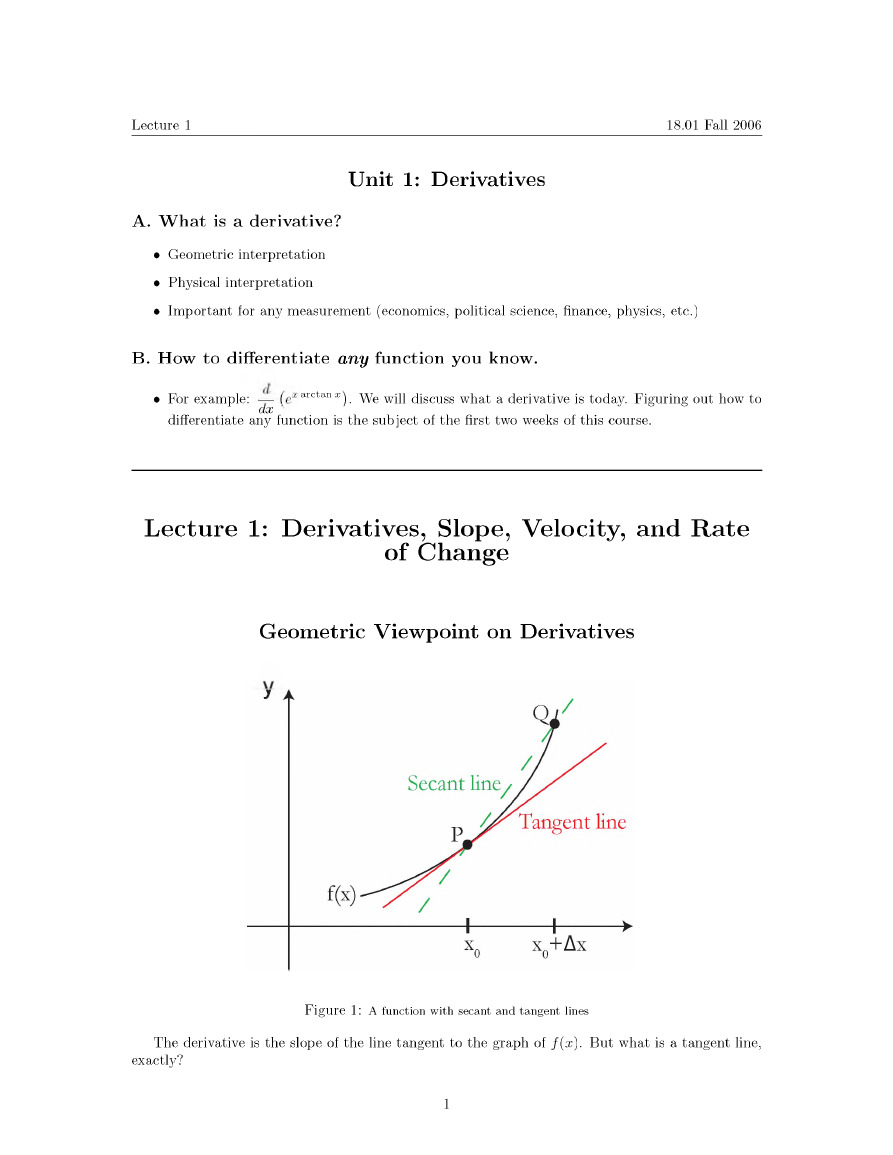
Figure 1 ： A function with secant and tangent lines
T h e derivative is the slope of the line tangent to the g r a p h of /(x). B u t w h a t is a tangent line,
exactl}^?
1
Lecture 1
18.01 Fall 2006
• It is N O T just a line that m e e t s the g r a p h at o n e point.
• It is the limit of the secant line (a line d r a w n b e t w e e n t w o points o n the graph) as the distance
b e t w e e n the t w o points goes to zero.
Geometric definition of the derivative:
Limit of slopes of secant lines P Q as Q ^ P ( P fixed). T h e slope of PQ:
Q
( x 〇+ A x , f ( x 〇+ A x ) )
Secant Line
limAx^O A x
lim / ( x 〇 十 A ：r) — / ( x 〇)
A x
“difference quotient”
f ( x 〇)
^derivative of / at x 〇r,
Example 1. f(x)
1
x
O n e thing to keep in m i n d w h e n w o r k i n g with derivatives: it m a y b e t e m p t i n g to plug in A x = 0
right away. If y o u d o this, however, y o u will always e n d u p with —— = 。 Y o u will always n e e d to
d o s o m e cancellation to get at the answer.
A x
0
A /
A x
l
A x
1
A x
x 〇 — (x〇 十 A x )
(x〇 十 A x ) x 〇
1
A x
—A x
- 1
(x〇 十 A x ) x 〇
(x〇 十 A x ) x 〇
T a k i n g the limit as A x ^ 0,
lim. ------ ---：— = —9
Xq
A x —0 (X〇 十 A x ) X 〇
2
Lecture 1
18.01 Fall 2006
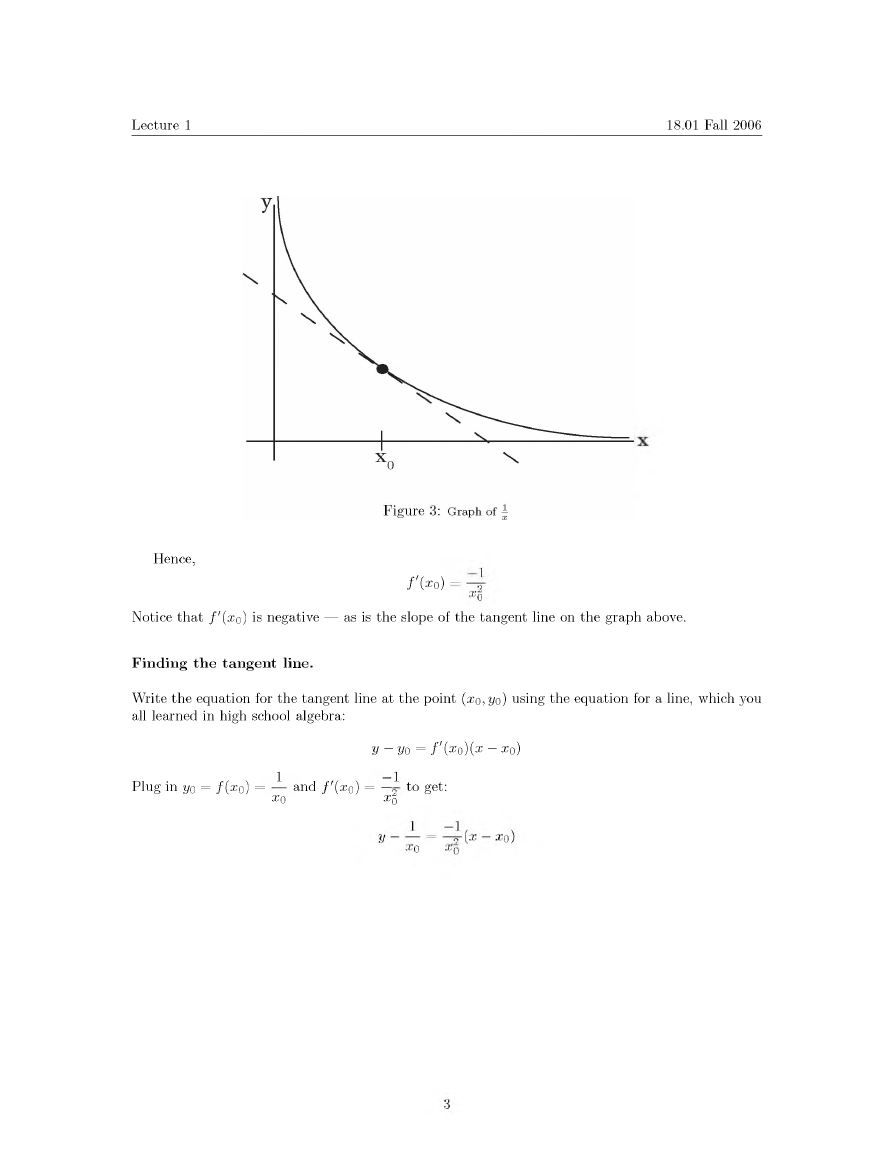
Hence,
f ' ( x 〇)
Notice that / ;(x〇) is negative —— as is the slope of the tangent line o n the g r a p h above.
Finding the tangent line.
Wri te the equation for the tangent line at the point (x〇,y〇) using the equation for a line, w h i c h }^ou
all learned in high school algebra:
y - y 〇 = ff(x〇)(x-x 〇)
P l u g in y 〇 = / ( x 〇) = — a n d / ;(x〇) = — to get:
'
1
X 〇
一 1
X g
Lecture 1
18.01 Fall 2006
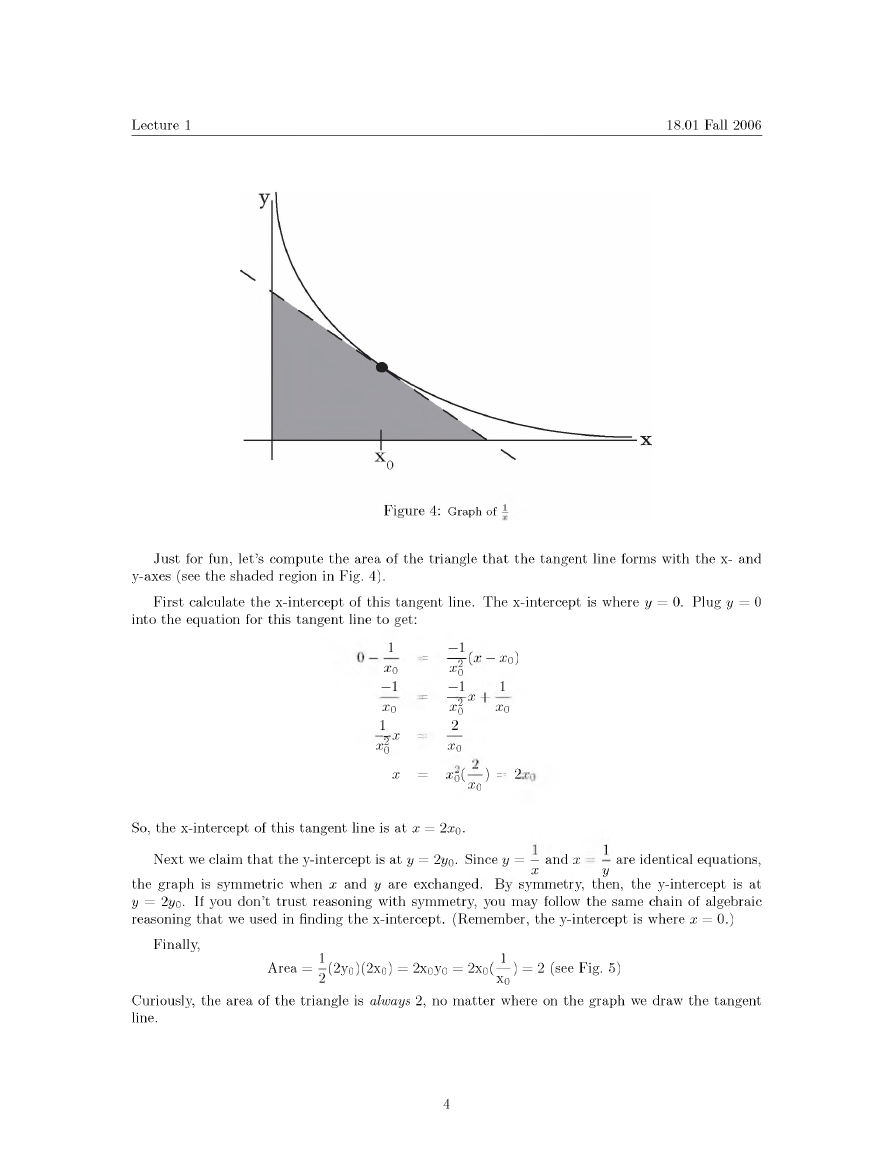
Just for fun, \eVs c o m p u t e the area of the triangle that the tangent line forms wi th the x- a n d
3^-axes (see the s h a d e d region in Fig. 4).
First calculate the x-intercept of this tangent line. T h e x-intercept is w h e r e y = 0. P l u g y = 0
into the equation for this tangent line to get:
1
x 〇
- 1
x 〇
1
_ 2"*^
x 0
=
=
r
- 1 .
x
0
- 1
- 2 X
x
0
2
---
x 〇
- X 〇)
~
1
x 〇
X
=
工 5 ( 二 ） = : 2
X〇
So, the x-intercept of this tangent line is at x = 2 x 〇.
N e x t w e claim that the 3^-intercept is at y = 2y〇. Since y = — a n d x = — are identical equations,
the g r a p h is s}^mmetric w h e n x a n d y are exchanged.
S3^mmetr}^ then, the 3^-intercept is at
y = 2 y 〇. If }，o u d o n ’t trust reasoning with S3，m m e t r } ，，}，o u m a } ，follow the s a m e chain of algebraic
reasoning that w e used in finding the x-intercept. ( R e m e m b e r , the 3^-intercept is w h e r e x = 0.)
x
y
Finall}，，
A r e a = i(2}，0)(2x0) = 2x 〇3,〇 = 2 x 〇(丄）= 2 (see Fig. 5)
1
x 〇
Curiousl}^, the area of the triangle is ahuays 2, n o m atter w h e r e o n the g r a p h w e d r a w the tangent
line.
4
Lecture 1
18.01 Fall 2006
Notations
Calculus, rather like English or an}^ other language, w a s developed
several people. A s a result,
just as there are man}^ wa}^s to express the s a m e thing, there are man}^ notations for the derivative.
Since y = /( ；r), it7s natural to write
Ay = A / = / 〇 ) - / 〇〇) = /〇〇 十 Ax) - / 〇〇)
W e sa)，“Delta y ” or “Delta / ” or the “c h a n g e in y ”.
If w e divide b o t h sides
A x = x — x 〇, w e get t w o expressions for the difference quotient:
T a k i n g the limit as A x ^ 0, w e get
A ^ = A /
A x
A x
A y
A x
A / 一
A x
dx (Leibniz7 notation)
/ ;(x〇) (Newton^s notation)
W h e n }^ou use Leibniz7 notation, }^ou have to r e m e m b e r w h e r e 3^ou7re evaluating the derivative
in the e x a m p l e above, at x = x 〇.
Other, equall}^ valid notations for the derivative of a function / include
df
/ ;, a n d D f
5
Lecture 1
18.01 Fall 2006
Example 2. f(x) = xn where n = 1,2, 3...
W h a t is -f-xn ?
ax
T o find it, plug y = f ( x ) into the definition of the difference quotient.
A y
A x
(x 〇 + A x ) n — Xq
(x + A x ) n — x n
A x
A x
( F r o m here on, w e replace x 〇 with x, so as to have less writing to do.) Since
(x + A x ) n = (x -\- A x ) ( x + Ax)...(x + A x ) n times
W e c a n rewrite this as
x n + n ( A x ) x n_1 + O ( ( A x ) 2)
O ( A x )2 is short h a n d for “all of the terms with ( A x ) 2，（A x ) 3 , a n d so o n u p to ( A x ) n .” （This is part
of w h a t is k n o w n as the binomial theorem; see your text b o o k for details.)
A y
A x
T a k e the limit:
Therefore,
(x + A x ) n — x n
x n + n ( A x ) ( x n _ 1 ) + O ( A x )2 — x n
A x
A x
= n x n_1 + O ( A x )
lim
A x ^ O A x
= nxn~ x
d n
—— x n == nxn~ 1
dx
This result extends to polynomials. For example,
d
dx (x2 十 3 x 10) = 2 x 十 3 0 x 9
Physical Interpretation of Derivatives
Y o u c a n think of the derivative as representing a rate of c h a n g e (speed is o n e e x a m p l e of this).
O n Halloween, M I T students have a tradition of dropp i n g p u m p k i n s f r o m the roof of this building,
w h i c h is a b o u t 4 0 0 feet high.
T h e equation of m o t i o n for objects near the ea r t h s surface (which w e will just accept for n o w )
implies that the height a b o v e the g r o u n d y of the p u m p k i n is:
y = 4 0 0 - 16t2
T h e average speed of the p u m p k i n (difference quotient) =
At
= ^ stance travelled
time elapsed
W h e n the p u m p k i n hits the ground, y = 0,
400 - 16t2 = 0
6
Lecture 1
18.01 Fall 2006
Solve to find t = 5. T h u s it takes 5 seconds for the p u m p k i n to reach the ground.
A v e r a g e s p e e d :
4 0 0 ft
5 sec
80 ft/s
A spectator is prob a b l y m o r e interested in h o w fast the p u m p k i n is going w h e n it slams into the
ground. T o find the instantaneous velocity at t = 5, lefs evaluate y f\
y f = —32t = (—32)(5) = —160 ft/s (about l l O m p h )
y' is negative because the p u m p k i n ^ y-coordinate is decreasing: it is m o v i n g d o w n w a r d .
7
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
