logo资料库

西安电子科技大学计算智能大作业-遗传算法.docx

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.29M 资料格式：docx 举报 版权申诉
第1页 / 共20页
第2页 / 共20页
第3页 / 共20页
第4页 / 共20页
第5页 / 共20页
第6页 / 共20页
第7页 / 共20页
第8页 / 共20页
资料共20页，剩余部分请下载后查看
    3.1基于遗传算法的图像增强
    3.2基于遗传算法的图像分割
    遗传算法在图像分割中最近几年的应用有很多，如
    3.3基于遗传算法的图像匹配
    3.4基于遗传算法的图像恢复
    3.5基于遗传算法的图像压缩
    课程名: 计算智能 论文名：遗传算法研究及应用 姓 名：xxx 学 号：xxxxxxxxxxx 专 业：xxxxxxx 2017 年 12 月 20 日
    摘 要 本文首先介绍了遗传算法的发展历史及研究现状，随着应用领域的不断扩大和实际工程问 题的复杂化，遗传算法逐渐显现出了一些不足和缺点，针对这些问题，一些改进的算法如多目 标优化遗传算法、小生境遗传算法相继被提出。对于遗传算法的主要研究内容，本文综述了参 数设置的选择、编码方法、遗传算子、模式定理、收敛性分析、和并行计算等，然后又介绍了 遗传算法在图像增强、图像分割、图像修复、图像配准以及图像压缩中最近几年的研究及应用。 最后，简单地总结了遗传算法的在图像处理中的研究趋势。虽然遗传算法在图像处理的应用中 还存在某些问题，但通过遗传算法的理论研究将会推动遗传算法理论及其应用的发展。 关键词：遗传算法 发展历史 研究综述 图像处理 1
    1. 遗传算法的发展 计算机技术的飞速发展使大规模的现实模拟成为可能，而针对社会和生物现象的模拟，对 人类认识自身及其环境具有重大意义，进化是其中最为诱人的领域之一[1]。人的智能是从哪里 来的？归根结底是从生物进化中得来的，反映在遗传基因中，脑的结构变化也是通过基因的变 化一代代遗传下来。每一种基因产生的生物染色体(看成一种结构)对环境有一定的适应性，或 叫适应度(fitness)，杂交和基因变异可能产生对环境适应性强的后代，通过优胜劣汰的自然选 择，适应度高的结构被保存下来[2]。因此从进化的观点看，结构是适应的结果。 遗传算法（GA 算法）是模拟前述生物进化过程的计算模型，它源于达尔文的进化论、孟 德尔的群体遗传学说和魏茨曼的物种选择学说；其基本思想是模拟自然界遗传机制和生物进化 论而形成的一种过程搜索最优解的算法[3]。遗传算法作为一种新的全局优化搜索算法，以其简 单通用、鲁棒性强、适于并行处理以及应用范围广等显著特点，奠定了它作为 21 世纪关键智 能计算之一的地位。 1.1 遗传算法的发展历史 遗传算法研究的兴起是在八十年代末和九十年代初期，但它的历史起源可追溯到六十年代 初期。遗传算法的创始人是美国的著名学者，密西根大学教授 Holland。Holland 在二十世纪五 十年代末期开始研究自然界的自适应现象，并希望能够将自然界的进化方法用于实现求解复杂 问题的自动程序设计。Holland 认为，可以用一组二进制串来模拟一组计算机程序，并且定义 了一个衡量每个“程序”的正确性的度量：适应值。Holland 模拟自然选择机制对这组“程序” 进行“进化”，直到最终得到一个正确的“程序”。1967 年，Bagley 发表了关于遗传算法应 用的论文，在其论文中首次使用了“遗传算法”(Genetic Algorithm)来命名 Holland 所提出的“进 化”方法。1970 年，Cavicchio 把遗传算法应用于模式识别中。第一个把遗传算法应用于函数 优化的是 Hollstien。1975 年，Holland 总结了自己的研究成果，发表了在遗传算法领域具有里 程碑意义的著作——《自然系统和人工系统的适应性》(Adaptation in Natural and Artificial Systems)。该书系统地阐述了遗传算法的基本理论和方法，并提出了对遗传算法的理论研究和 发展极为重要的模式理论（schemata theory），该理论首次确认了结构重组遗传操作对于获得 隐并行性的重要性[4]。在这本书中，Holland 为所有的适应系统建立了一种通用理论框架，并展 示了如何将自然界的进化过程应用到人工系统中去。Holland 认为，所有的适应问题都可以表 示为“遗传”问题，并用“进化”方法来解决。同年，DeJong 完成了他的重要论文《遗传自 适应系统的行为分析》。他在该论文中所做的研究工作可看作是遗传算法发展过程中的一个里 程碑，这是因为他把 Holland 的模式理论与他的计算使用结合起来。在一系列研究工作的基础 上，上世纪 80 年代由 Goldberg 进行归纳总结，形成了遗传算法的基本框架。 人们通常把 Holland 所提出的遗传算法称为简单遗传算法或标准遗传算法，简记为 SGA[5]。 在 Holland 的简单遗传算法基础上，人们不断对之进行各种的改进和完善，并将 SGA 与其它算 法相结合解决各自不同领域的问题。从公开发表的论文看，我国首先开始研究应用遗传算法的 有赵改善[6]和华中理工大学的师汉民等人[7]。遗传算法最早应用于一维地震波形反演中[8]，其特 点是处理的对象是参数的编码集而不是问题参数本身，搜索过程既不受优化函数联系性的约 束，也不要求优化函数可导，具有较好的全局搜索能力；算法的基本思想简单，运行方式和实 现步骤规范，具有全局并行搜索、简单通用、鲁棒性强等优点，但其局部搜索能力差，容易出 现早熟现象[9]。 随着技术的不断进步与发展，遗传算法的研究也在不断深入，无论在理论研究方面，还是 在实际应用方面都有了长足的进展。特别是近年来全世界范围内的进化计算热潮，计算智能作 为人工智能的重要研究方向，使得遗传算法受到更广泛关注。1997 年 5 月 IEEE 的（Transaction on Evolutionary Computation）创刊，遗传算法作为具有系统优化、自适应和学习的高性能计算 2
    和建模方法的研究日益成熟[10]。 1.2 遗传算法的发展 自 Holland 教授首次提出遗传算法后，遗传算法作为求解问题的一类自组织与自适应的人 工智能技术，被广泛研究和应用。随着应用领域的不断扩大和实际工程问题的复杂化，遗传算 法逐渐显现出了一些不足和缺点，针对这些问题，一些改进的算法相继被提出。 1.2.1 保持物种多样性的遗传算法 为保持个体间的多样性提出了一种基于多样化成长策略的遗传算法［11］。基于信息熵度量 多目标空间下群体的多样性，提出了一种保持群体多样性的多目标遗传算法［12］。针对多目标 作业车间调度问题，提出了一种双种群遗传算法，该算法将正、逆序调度算法与生成调度活动 的遗传算法有效地结合了起来［13］。在借鉴生物遗传学的基础上提出了一种多群体阶段性杂交 遗传算法［14］。在种群进化进程中，根据采用一定方法能有效缩小搜索区域、动态改变种群规 模的思想，提出了一种变搜索区域多种群遗传算法［15］。一种基于熵的双群体遗传算法，通过 提高初始化群体的熵值和保持进化过程群体的熵值，有效地保持了遗传群体的个体多样性［16］。 1.2.2 多目标优化遗传算法 在非劣分层遗传算法的基础上，提出了加入局部搜索的多目标遗传算法及适用于多目标优 化的模拟退火局部搜索算法和跳转准则，弥补了遗传算法中局部搜索能力差、易早熟的缺［17］ 点。将任意多个目标函数的优化问题转换成两个目标函数的优化问题，并对转换后的优化问题 设计了遗传算法［18］。通过在不同准则之间引入偏好来解决一些算法不能有效处理目标数目较 多时的优化问题，提出了一种多目标调和遗传算法( MOCGA) 。将随机逼近算法( SPSA) 的 快速局部优化方法与遗传算法的整体搜索策略结［19］合起来，提出了一种解决多目标优化问题 的随机梯度遗传算法［20］，基于精英选择和个体迁移的多目标遗传算法求解多目标优化问题的 方法［21］。 1.2.3 约束处理 为了给一般的非线性双层规划问题提供一种简单易操作的有效算法，提出了一种基于插值 的解非线性双层规划的遗传算法［22］。为了在非凸非线性规划问题中获得全局最优解，提出了 一种新技术，通过变量的上下界将主要问题分成若干子问题，减少种群规模，从而在合理的时 间内达到全局最优［23］，还有人提出了一种新的遗传算法解决约束优化问题［24］。提出了一种基 于物种选择的遗传算法，通过缩小最优种群约束边界来提高局部搜索速度，并提出了一种新的 惩罚因子计算法［25］，即 （1） 其中：种群个数为 p，可行点个数为 p1，则不可行点个数为 p－p1；可行域标记为Γ，标准差 函数为 std，通过采用两次计算惩罚因子的办法来处理约束条件。 结合遗传算法和自组织迁移算法的特点，提出了一种自组织迁移遗传算法求解约束优化， 使用惩罚函数来处理选择操作［26］，惩罚函数如下： 其中：Gk 为海维赛德算子。 为处理约束问题，可以在遗传算法中采用不需要任何惩罚参数的小生境惩罚方法［27］，惩 （2） 3
    罚计算如下: （3） f 是种群中所有可行解的最大函数值。在锦标赛选择算子中执行共享策略。 其中： max 1.2.4 小生境遗传算法 有研究人员提出了一种基于社团划分的小生境遗传算法，运用 GN 算法划分超级个体关系 网以获取生境，并提取生境中共有模式［28］，提出了一种面向多模态函数优化的自适应小生境 遗传算法，通过引入小生境熵来度量种群多样性，并利用小生境熵自适应调整进化参数取值; 同时为了提高算法的全局搜索能力和局部收敛速度，在识别出的小生境范围内进行境外、境内 交叉 ［ 29 ］，提出了一种解决连续多模态优化问题的小生境混合遗传算法，将小生境技术和 Nelder-Mead 的单一方法有机地融合在遗传算法中，加强了算法的搜索能力［30］。 1.2.5 混合算法 混合遗传算法的实质是将不同算法的优点有机结合，改善单纯 GA 的性能。基于量子位的 混沌特性和相干特性，有文献提出了一种实数编码混沌量子遗传算法(RCQGA)［31］。通过将量 子位染色体转换成可变界线编码的染色体，提出了一种新的量子遗传算法［32］。将遗传算法与 信赖域方法有机结合，提出了一种信赖域遗传算法，改变了信赖域方法求解多峰值优化不能收 敛到全局最优的问题，对接近二次函数的优化问题具有较强的优势［33］。在标准遗传算法的基 础上，通过改进选择概率提出了一种自适应退火遗传算法。结合蚁群算法很强的局部收敛能力 和遗传算法快速的全局搜索能力［34］，提出了一种带有参数自适应调节能力的混合算法［35］。结 合模糊推理、模拟退火算法和自适应机制，提出了一种模糊自适应模拟退火遗传算法(FASAGA) ［36］。在分析柔性作业车间调度问题特性的基础上，在文化算法的知识源中引入遗传算法，提 出一种采用主群体空间和信仰空间的双层进化结构的调度算法［37］。有文献提出了一种基于结 合神经网络和遗传算法的混合优化算法，在算法中，反向传播神经网络被用于改善遗传算法在 寻找全局最优时的收敛性［38］。 基因表达式编程(gene expression programming，GEP)［39］是在继承和发扬遗传算法与遗传 编程(genetic programming，GP)优点的基础上发展起来的进化计算家族中的新成员，其结合了 遗传算法的简单线性染色体思想和 GP 中使用的大小和形状不同的分叉结构思想。为保持种群 的多样性，采用了基因空间均匀分布策略、自适应交叉和变异算子以及淘汰算子等方法，提出 了一种基于多样化进化策略的基因表达式编程算法 DS-GEP［40］。通过引入同源基因和细胞系 统思想，提出了一种基于多细胞基因表达式编程的函数优化新算法，以求解函数优化问题［41］。 1.2.6 改进的遗传算法 受蜜蜂繁殖进化方式启发，提出了一种新型的遗传算法—蜜蜂进化型遗传算法(BEGA)［42］。 通过借鉴遗传算法的思想，利用云模型云滴的随机性和稳定倾向性的特点提出了云遗传算法 (CGA)［43］。据元胞个体密度与分布的演化规则，提出具有演化规则的元胞遗传算法(CEGA)［44］。 有学者提出了一种自组织遗传算法来优化 PID 控制器的参数，提高了标准遗传算法的全局搜 索效率，避免了早熟收敛［45］。通过分析现存遗传算子的不足和生物进化的基本特征，设计了 一种智能仿生遗传算法［46］。由于简单遗传算法在解决复杂优化问题时速度慢、易陷入局部收 敛，提出了一种逐渐减少优化搜索范围的改进遗传算法［47］。 1.2.7 新型算法 结合遗传算法、关系网模型提出了一种基于智能体的多目标社会进化算法求解多目标优化 问题［47］。针对二进制编码方式设计了族群分类方法，并在该族群结构的基础上形成了具有双 轨协同进化特征的族群进化算法以及相应的族群算子［48］。基于种群中适应度较高的个体对种 群的进化有推动作用这一思想，提出了一种适用于求解约束优化问题的 M-精英协同进化算法 4
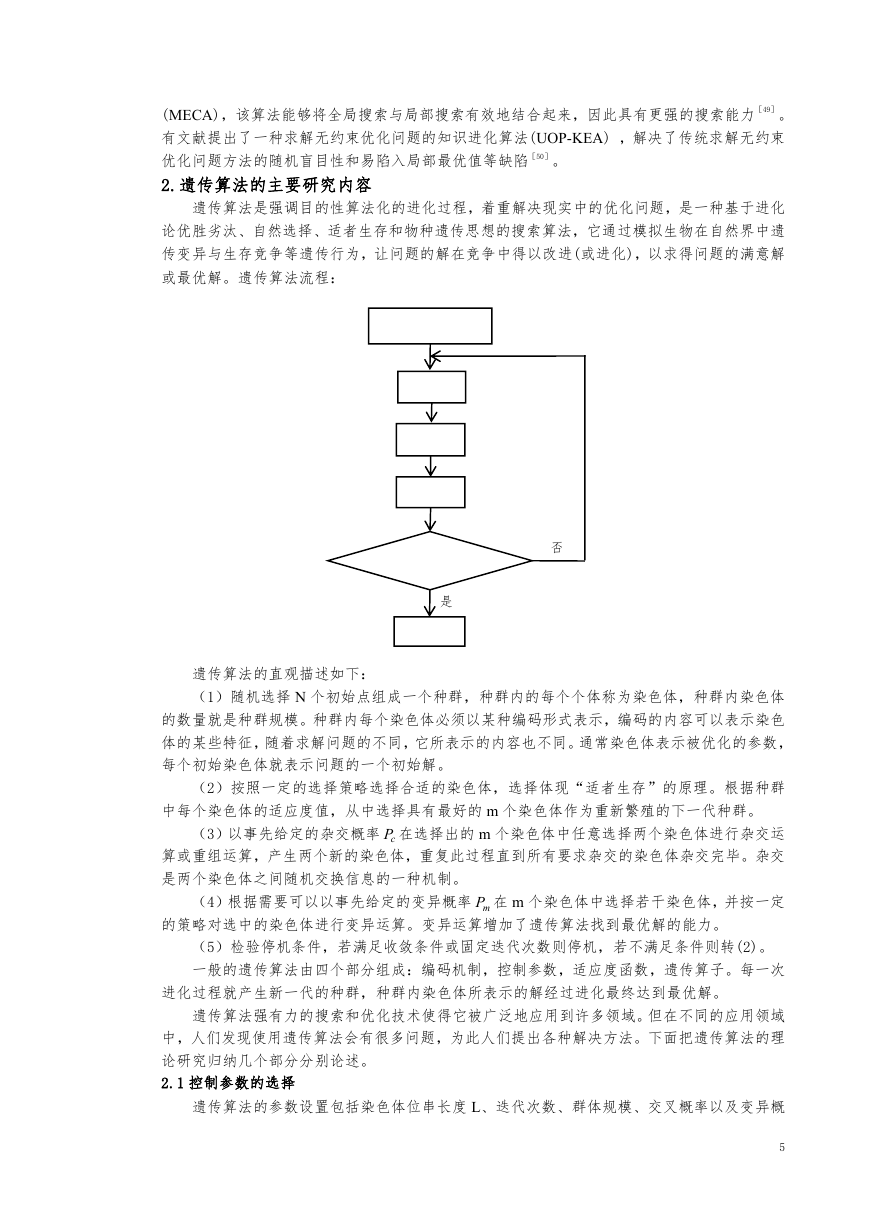
    (MECA)，该算法能够将全局搜索与局部搜索有效地结合起来，因此具有更强的搜索能力［49］。 有文献提出了一种求解无约束优化问题的知识进化算法(UOP-KEA) ，解决了传统求解无约束 优化问题方法的随机盲目性和易陷入局部最优值等缺陷［50］。 2.遗传算法的主要研究内容 遗传算法是强调目的性算法化的进化过程，着重解决现实中的优化问题，是一种基于进化 论优胜劣汰、自然选择、适者生存和物种遗传思想的搜索算法，它通过模拟生物在自然界中遗 传变异与生存竞争等遗传行为，让问题的解在竞争中得以改进(或进化)，以求得问题的满意解 或最优解。遗传算法流程： 初始种群生成 选择 交叉 变异 满足结束条件 否 是 结束 遗传算法的直观描述如下： （1）随机选择 N 个初始点组成一个种群，种群内的每个个体称为染色体，种群内染色体 的数量就是种群规模。种群内每个染色体必须以某种编码形式表示，编码的内容可以表示染色 体的某些特征，随着求解问题的不同，它所表示的内容也不同。通常染色体表示被优化的参数， 每个初始染色体就表示问题的一个初始解。 （2）按照一定的选择策略选择合适的染色体，选择体现“适者生存”的原理。根据种群 中每个染色体的适应度值，从中选择具有最好的 m 个染色体作为重新繁殖的下一代种群。 （3）以事先给定的杂交概率 cP 在选择出的 m 个染色体中任意选择两个染色体进行杂交运 算或重组运算，产生两个新的染色体，重复此过程直到所有要求杂交的染色体杂交完毕。杂交 是两个染色体之间随机交换信息的一种机制。 （4）根据需要可以以事先给定的变异概率 mP 在 m 个染色体中选择若干染色体，并按一定 的策略对选中的染色体进行变异运算。变异运算增加了遗传算法找到最优解的能力。 （5）检验停机条件，若满足收敛条件或固定迭代次数则停机，若不满足条件则转(2)。 一般的遗传算法由四个部分组成：编码机制，控制参数，适应度函数，遗传算子。每一次 进化过程就产生新一代的种群，种群内染色体所表示的解经过进化最终达到最优解。 遗传算法强有力的搜索和优化技术使得它被广泛地应用到许多领域。但在不同的应用领域 中，人们发现使用遗传算法会有很多问题，为此人们提出各种解决方法。下面把遗传算法的理 论研究归纳几个部分分别论述。 2.1 控制参数的选择 遗传算法的参数设置包括染色体位串长度 L、迭代次数、群体规模、交叉概率以及变异概 5
    率等。目前对遗传算法的参数设置的合理选择还缺少相应的理论作为指导。由于参数设置关系 到遗传算法的精度、可靠性和计算时间等诸多因素，并且影响结果的质量和系统性能，因此， 参数设置的研究受到重视。 遗传算法的运行过程中，存在着对其性能产生重大影响的一组参数。这组参数在初始化阶 段或群体进化过程中需要合理的选择和控制，以使遗传算法得到最佳的效果。主要参数有：染 色体位串长度 L，群体规模，交叉概率以及变异概率。大量的实验研究给出了最优参数建议： （1）位串长度 L：位串长度 L 的选择取决于特定问题解的精度。要求的精度越高，位串 越长，但需要的计算时间也长。 （2）群体规模 N：大群体含有较多模式，为遗传算法提供了足够的模式采样容量，可以 改进遗传算法的搜索质量，防止成熟前收敛。但大群体增加了个体适应值的计算量，使得收敛 速度降低。一般情况下专家建议 N=20~200。 （3）交叉概率 cP ：交叉概率控制着交叉算子的应用频率，在每一代新的群体中需要对 N × cP 个个体的染色体结构进行交叉操作。交叉概率越高，群体引入新结构越快，但已获得的优 良基因丢失的也快；反之，交叉概率太低则搜索可能停滞不前。 （4）变异概率 mP ：变异操作是保持种群多样性的有效手段，交叉结束后，全部新个体位 串上的每位等位基因按变异概率 mP 随机改变，每代中大约发生 L×N× mP 次变异。变异概率 越小，可能使得某些基因为过早丢失的信息无法恢复；但变异概率越高，则遗传搜索就退化为 随机搜索。 实际上，上述参数的选择往往与具体的问题有直接联系。问题的目标函数越复杂，参数的 选择就越困难。理论上来说，不存在普遍适应的一组最佳参数。 孙艳丰证明，当采用自然数编码时，从理论上可以证明遗传算法的最优群体规模的存在性， 并给出相应的计算方法。但在大多数情况下，群体规模的大小是很难进行计算，理论上讲不同 的解题过程应该有不同的最佳群体规模。如果群体规模太小，由于群体中的模式缺少使得遗传 算法受到搜索空间的限制。如果群体规模太大，则搜索和优化需要花费大量的时间。 迭代次数的设置分为固定和不固定两种设置。固定迭代次数有利于遗传算法的处理，但设 置选择困难，并且不利于产生最优解。不固定迭代次数通过对个体解的判断自动进行迭代有利 于产生最优解，并且解决了参数选择的困难，但容易增加遗传算法的处理时间，尤其是在算法 发散时。最佳群体规模和迭代次数的设置研究目前很少有报道。通常，群体规模和迭代次数的 设置是根据经验或实验进行的。 对杂交概率 cP 和变异概率 mP 的设置，由于它们关系到遗传算法的收敛性和群体中个体的 多样性，即探索和开发问题，因此倍受重视。传统的 cP 和 mP 的设置是静态人工设置。现在有 人提出动态参数设置的方法，以减少人工选择参数的困难和盲目性。Srinivas et al.提出用自适 应杂交概率和变异概率来实现两个目的：维持群体的多样性和保证遗传算法的收敛性。探索问 题是指在寻找全局最优解时能探索新的解空间区域；开发问题是指在探索到最优解区域时能收 敛到最优解。两者的平衡由 cP 和 mP 值决定。 cP 和 mP 值增加，则以开发为代价提高探索过程。 增加探索过程也就增加个体的变化，却降低了个体适应性值。这有利于探索各种解空间，保证 解的全局性，但不利于群体收敛到最优解。而 cP 和 mP 值降低，则以探索为代价提高开发过程。 增加开发过程即增加个体适应性值，减少个体的变化，有助于群体收敛到最优解，但不能保证 全局最优解。因此由算法自动设置 cP 和 mP 是必要的。 目前许多学者意识到这些参数应该随着遗传进化而自适应变化，Davis 提出自适应算子概 率的方法，即用自适应机制把算子概率的选择与算子产生的个体适应性结合，高适应性值被分 配高算子概率。Fogarty 研究了变异率对整数编码的影响。Whiley 提出一种自适应变异策略与 一对父串间的 Hamming 距离成反比，结果显示能有效地保持基因的多样性。张良杰等通过引 入 i 位改进子空间概念，采用模糊推理技术来确定选取变异概率的一般性原则。 6
    2.2 适应函数 遗传算法将问题空间表示成染色体位串空间，为了执行适者生存的原则，必须对各个体的 染色体位串的适应性进行评价。所以，适应函数就构成了个体的生存空间。根据个体的适应值 就可以确定该个体在此环境下的生存能力，一般来说好的染色体位串具有较高的适应值，具有 较强的生存能力。 适应值是群体中各个体的生存机会选择的唯一标准，选择的好坏直接影响算法的优劣，所 以适应函数的形式直接决定着群体的进化行为。为了能够直接将适应函数与群体中的个体优劣 量度相联系，在遗传算法中规定适应值为非负值，且在任何情况下越大越好。引入适应值调节 和资源共享策略可以加快收敛速度和跳出局部最优点。对适应值进行调节就是通过变换改变原 适应值间的比例关系，常用的比例变换有线性变换、乘幂变换和指数变换等。 针对某一给定的问题，目标函数可能有正有负，甚至是复数，故此必须建立适应函数与目 标函数的映射关系，从而保证映射后的适应值是非负值，且目标函数的优化方向应对适应值增 大的方向。 2.3 选择策略 优胜劣汰的选择机制使得适应值大的染色体有较大的存活机会，不同的选择策略对算法性 能有较大的影响，轮盘赌法是使用最多的选择策略，但这种策略可能会产生较大的抽样误差， 于是对此提出了很多的改进方法，如繁殖池选择，Boltzmann 选择等等，但是这几种策略都是 基于适应值比例的选择，常常会出现早熟收敛现象和停滞现象。为此人们又提出了非线性排名 选择，这种选择不仅避免了上述问题，而且可以直接使用原始适应值进行排名选择，而不需对 适应值进行标准化。但这种选择在种群规模很大时，其额外计算量(如计算总体适应值和排序) 也相当可观，甚至在进行并行实现时有时要带来一些同步限制。基于局部竞争机制的选择如 (  )选择，它使双亲和后代有同样的生存竞争机会，在一定程度上避免了这些问题。 2.4 编码方法 编码方法是 GA 的基础。GA 不是对研究对象直接进行讨论，而是通过某种编码机制把对 象统一由特定符号(字母)按一定顺序排成串（string）。正如研究生物遗传，是从染色体着手， 染色体则是由基因排成的串。在 SGA 中，字符集由 O 与 1 组成，码为二进串。对一般的 GA， 自然可不受此限制。串的集合构成总体，染色体就是串。对 GA 的码可以有十分广泛的理解。 在优化问题中，一个串对应于一个可能解，在分类问题，串可解释为一个规则，即串的前半部 为输入或前件，后半部为输出或后件、结论，等等。这也正是 GA 有广泛应用的重要原因。按 照遗传算法的工作流程，用遗传算法求解的首要问题就是在目标问题实际表示与遗传算法的染 色体位串结构之间建立联系，即编码和解码运算。由于遗传算法计算过程 的鲁棒性，它对编码的要求并不苛刻。一般来说，问题编码应满足以下 3 个原则： （1）完备性：问题空间中的所有潜在解都能成为遗传算法编码空间中的染色体位 串的表现性； （2）健全性：遗传算法编码空间中的染色体位串必须对应问题空间中的某一个潜 在解； （3）非冗余性：染色体和潜在解必须一一对应。 Hol1and 在运用模式定理分析编码机制时，建议使用二进制编码，但二进制编码不能直接 反映问题的固有结构，精度不高，染色体长度大，占用计算机内存多。遗传算法对被优化的参 数(用个体表示)进行编码，并以编码方式运算。对参数编码的目的是把一个优化问题变成一个 组合问题。根据应用的不同，遗传算法的搜索空间可以分为连续空间和离散空间，分别称为连 续遗传算法和离散遗传算法(即标准遗传算法)。在离散遗传算法中，染色体编码常用的方法是 有限长度二进制编码，其优点是有利于遗传算法建立数学模型，并便于诸如模式定理、收敛性 7
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料