第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
2020-2021学年天津市南开区七年级上册期末数学试卷及答案.doc
2020-2021 学年天津市南开区七年级上册期末数学试卷及答
案
注意事项：
1．答第Ⅰ卷前，考生务必先将自己的姓名、准考让号，用蓝、黑色墨水的钢笔或圆珠笔填
写在“答题卡”上．
2．答案答在试卷上无效，每小题选出谷案后，用 2B 铅笔把“答题卡”上对应题目答案的序
号的信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案．
3．考试结束后，监考人员将试卷和答题卡一并收回．
一、选择题：本大题共 12 小题，每道题 3 分，共 36 分，再每小题给出的四个选项中，只有
一个项是符合题目要求的．
1. 如果升降机下降10 米记作 10 米，那么上升15 米记作（ ）米
A.
15
【答案】B
B.
15
C.
10
D.
10
2. 绝对值大于 1 而小于 4 的整数有（ ）个
A. 1
【答案】D
B. 2
C. 3
D. 4
3. 下列判断正确的是（
）
A.
2
2
x y 的次数是 2
C.
2
3
2
a b 的系数是
2
3
【答案】D
B. 0 不是单项式
D.
4
3
x
2
2
x
6
是四次三项式
4. 将一副直角三角尺按如图所示的不同方式摆放，则图中∠α与∠β相等的是（
）
A.
C.
B.
D.
【答案】C
5. 《算法统宗》是我国古代数学著作，其中记载了一道数学问题大意如下：若将绳子三折
后测井深则多 4 尺；若将绳子四折去测井深则多 1 尺．问绳长和井深各多少尺？设井深为 x
尺，则可列方程为（
）
A. 3（x+4）＝4（x+1）
C. 3（x﹣4）＝4（x﹣1）
【答案】A
B. 3x+4＝4x+1
D.
x
3
﹣4＝
x
4
﹣1
6. 已知∠α＝27′，∠β＝0.45°，则∠α与∠β的大小关系是（
）
A. ∠α＝∠β
B. ∠α＞∠β
C. ∠α＜∠β
D. 无法确
定
【答案】A
7. 如图，射线 OC的端点 O在直线 AB上，∠AOC的度数比∠BOC的 2 倍多 10 度．设∠AOC
和∠BOC的度数分别为 x，y，则下列正确的方程组为（
）
A.
C.
x
y
x
y
180
10
x
x
180
y
10 2
y
【答案】B
B.
D.
x
x
y
y
2
180
10
x
y
y
2
x
180
10
8. 如图，B、C 两点把线段 MN 分成三部分，其比为 MB：BC：CN＝2：3：4，点 P 是 MN 的中
点，PC＝2cm，则 MN 的长为（
）
A. 30cm
【答案】B
B. 36cm
C. 40cm
D. 48cm
9. 钟表上 8 点 30 分时，时针与分针的夹角为（ ）
A. 15°
【答案】C
B. 30°
C. 75°
D. 60°
10. 如图，直线 AB与 CD相交于点 O，∠DOE＝α，∠DOF：∠AOD＝2：3，射线 OE平分∠BOF，
则∠BOC＝（
）
A. 540°﹣5α
B. 540°﹣6α
C. 30°
D. 40°
【答案】B
11. 若 ab≠0，那么
|
|
a
a
A. ﹣2
【答案】C
|
的取值不可能是（
|
b
b
B. 0
）
C. 1
D. 2
12. 已知：线段 AB，点 P 是直线 AB 上一点，直线上共有 3 条线段：AB，PA 和 PB，若其中
有一条线段的长度是另一条线段长度的两倍，则称点 P 是线段 AB 的“巧分点”，线段 AB 的
“巧分点”的个数是（ ）
A. 6
【答案】C
B. 8
C. 9
D. 10
第Ⅱ卷（非选择题，共 64 分）
二、填空题：本大题共 6 小题，每小题 3 分，共 18 分．请将答案直接填在答题纸中对应的
横线上
13. 据有关报道，2020 年某市斥资约 5 800 000 元改造老旧小区，数据 5 800 000 科学记
数法表示为_________．
【答案】5.8×106．
14. 若 a，b 互为相反数，c，d 互为倒数，则 2021（a＋b）－2020cd＝___．
【答案】 2020
15. 直线 AB ， BC ，CA 的位置关系如图所示，则下列语句：
①点 B 在直线 BC 上；②直线 AB 经过点C ；③直线 AB ， BC ，CA 两两相交；④点 B 是
直线 AB ， BC 的交点．
以上语句正确的有________．（只填写序号）
【答案】①③④
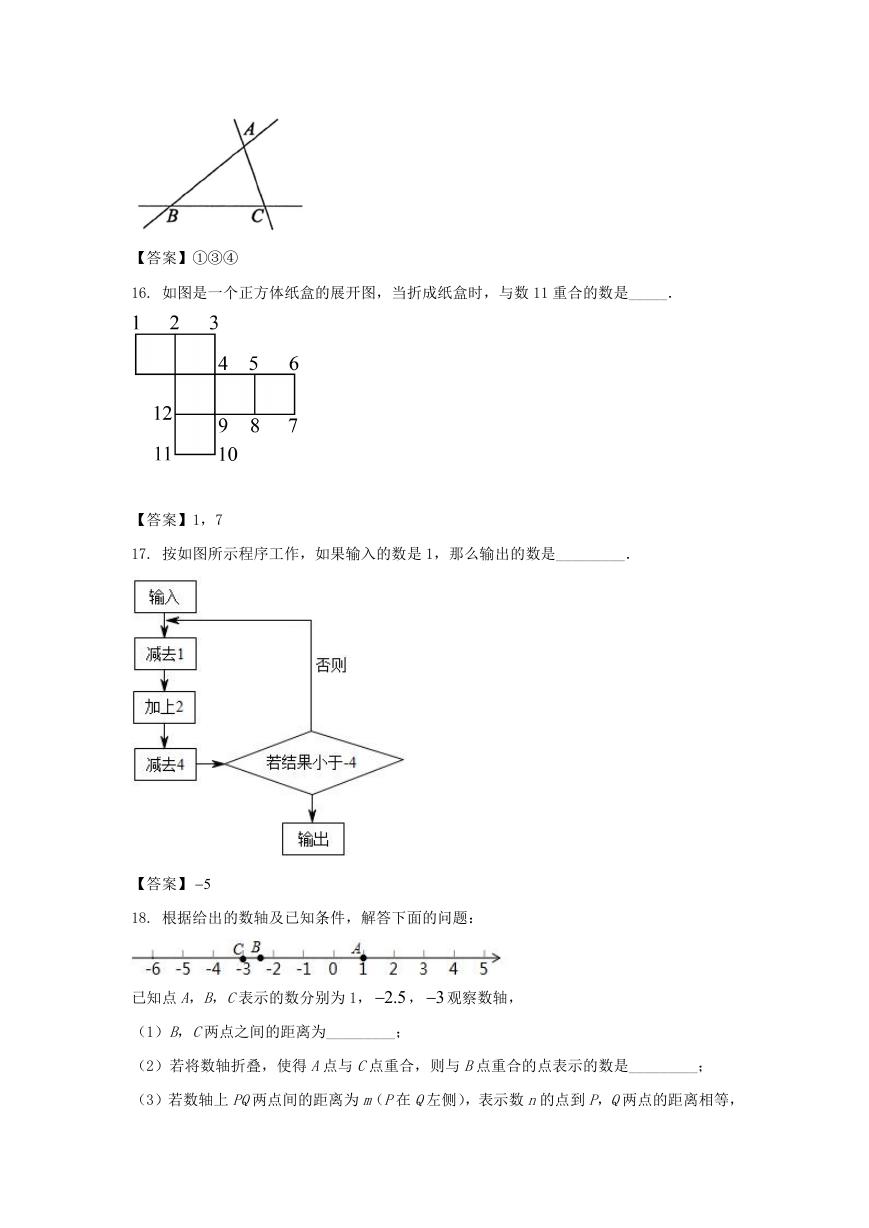
16. 如图是一个正方体纸盒的展开图，当折成纸盒时，与数 11 重合的数是_____．
【答案】1，7
17. 按如图所示程序工作，如果输入的数是 1，那么输出的数是_________．
【答案】 5
18. 根据给出的数轴及已知条件，解答下面的问题：
已知点 A，B，C表示的数分别为 1， 2.5 ， 3 观察数轴，
（1）B，C两点之间的距离为_________；
（2）若将数轴折叠，使得 A点与 C点重合，则与 B点重合的点表示的数是_________；
（3）若数轴上 PQ两点间的距离为 m（P在 Q左侧），表示数 n的点到 P，Q两点的距离相等，
则将数轴折叠，使得 P点与 Q点重合时，Q点代表的数_________（用含 m，n的式子表示这
个数）．
【答案】
①. 0.5
②. 0.5
③.
mn
2
三、解答题（共 46 分）
19. 计算
（1）
( 1)
1000
2.45 8 2.55 ( 8)
．
（2） 2
2
5
3
1
5
25 0
．
【答案】（1）-41；（2）-2
（1）先计算整数指数幂和利用乘法结合律计算（注意符号的变化），再进行加、减、乘、除
计算即可．
（2）先计算整数指数幂，分数乘法，去绝对值，整数乘法，再进行加、减计算即可．
【详解】（1）
( 1)
1000
2.45 8 2.55 ( 8)
1 (2.45 2.55)
( 8)
1 5
8
41
（2） 2
2
5
3
1
5
25 0
4 1 3 0
5 3
2
20. 如图所示，已知 O是直线 AB上一点，
BOE
FOD
90
，OB平分 COD
．
（1）图中与 DOE
（2）图中与 DOE
（3）图中与 DOE
相等角有_______________________
互余的角有________________________
互补的角有________________________
【答案】（1） AOF
（1）由题意可知
；（2） BOD
EOF
AOF
， EOF
90
，
， BOC
DOE
；（3） BOF
， COE
EOF
90
，即得到与 DOE
相
等的角为 AOF
．
（2）由 OB 平分 COD
可得 BOC
BOD
，再由（1）即易证
EOF
BOD
．最后即可知与 DOE
BOC
180
BOD
（3）由（2）知 EOF
互余的角为 BOD
，即证明 BOF
，即可知与 DOE
DOE
AOF
BOF
和
90
，
BOD
、 BOC
DOE
、 EOF
COE
互补的角为 BOF
，又由
．
、
AOF
COE
．
【详解】（1）∵
，
BOE
AOE
90
EOF
， EOF
DOE
相等的角为 AOF
DOE
．
∴
AOF
∴ AOF
故与 DOE
BOD
．
FOD
EOF
90
，
90
，
DOE
BOD
90
．
（2）∵OB 平分 COD
，
∴ BOC
BOD
，
又由（1）可知
BOD
90
， EOF
BOD
．
180
,
COE
DOE
、 COE
3 a b 1
．
2
2
2
2ab
1
，其中a
2 ，
b
．
1
4
【答案】 2a b 4
，3．
直接利用整式的加减运算法则分别化简合并同类项，进而把已知代入即可．
【详解】解：
2
2 a b ab
2
3 a b 1
2
2
2ab
1
、 EOF
、 BOC
．
BOD
， COE
BOC
，
BOE
BOC
，
DOE
90
．
EOF
∴
DOE
BOC
互余的角为 BOD
故与 DOE
（3）由（2）可知 EOF
∵ BOF
BOE
∴ BOF
COE
由（1）可知 AOF
BOF
BOF
互补的角为 BOF
DOE
180
180
故与 DOE
21. 先化简，再求值：
AOF
DOE
，
∵
∴
2
，
2 a b ab
2
2a b 2ab
2
2
3a b 3 2ab
2
1
，
2a b 4
，
把 a
2 ，
b
代入上式得：原式
1
4
22. 解方程或方程组
．
2
2
4
3
1
4
（1）解方程： 2(10 0.5 )
y
(1.5
y
2)
（2）解方程：
2(
6(
x
3
x
y
y
y
)
x
4
) 4(2
x
1
y
) 16
【答案】（1）
y ；（2）
44
x
y
2
2
．
（1）首先进行去括号，然后移项合并求解即可；
（2）先分别对两个方程进行整理化简，然后运用加减消元法求解即可．
【详解】（1） 2(10 0.5 )
y
(1.5
y
2)
解：去括号，得： 20
y
1.5
y
，
2
移项，得：
y
1.5
y
，
2 20
合并，得： 0.5
y ，
22
解得：
y ．
44
（2）
2(
6(
x
3
x
y
y
y
)
x
4
) 4(2
x
1
y
) 16
解：
8(
6(
x
x
) 3(
x
y
) 4(2
y
x
y
)
12
) 16
y
5
x
2
x
11
y
10
y
12
16
①
②
①×2＋②×5 得
28
y
56
y
2
把 2
y 代入②得 2
x
∴
x
y
2
2
．
23. 整理一批图书，由一个人做要 40h 完成，现计划由一部分人先做 4h，然后增加 2 人与
他们一起做 8h，完成这项工作，假设这些人的工作效率相同，具体应先安排多少人工作？
【答案】应安排 2 人先做 4h．
设安排 x人先做 4h，然后根据先后两个时段的工作量之和等于总工作量，可列方程求解．
【详解】解：设安排 x人先做 4h，
由题意得：
4
x
40
8(
x
40
2)
1
解得 2
x ，
∴应安排 2 人先做 4h，
答：应安排 2 人先做 4h．
24. 已知点C 在线段 AB 上，
AB ，
18
DE ，线段 DE 在线段 AB 上移动．
8
AC
2
BC
，点 D 、E 在直线 AB 上，点 D 在点 E 的左侧．若
（1）如图 1，当 E 为 BC 中点时，求 AD 的长；
（2）点 F （异于 A ， B ，C 点）在线段 AB 上，
AF
AD
3
，
CE EF
，求 AD 的
3
长．
【答案】（1）7
（2）3 或 5
（1）根据
AC
2
BC
，
AB ，可求得
18
BC ，
6
AC ，根据中点的定义求出 BE，
12
由线段的和差即可得到 AD的长．
（2）点 F（异于 A，B，C点）在线段 AB上，
AF
AD
3
，
CE EF
，确定点 F是 BC
3
的中点，即可求出 AD的长．
【小问 1 详解】
AC
BC
，
2
BC
6
，
AB ，
AC ，
18
12
如图 1，
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
