基于RBF 神经网络分位数回归的概率密度预测方法.pdf

发布时间：2022-06-01 发布人：admin 分类：说明书资料大小：0.73M 资料格式：pdf 举报版权申诉

challenger_yu-10360455-4744302542869753396.pdf-第1页.png

第1页 / 共6页

challenger_yu-10360455-4744302542869753396.pdf-第2页.png

第2页 / 共6页

challenger_yu-10360455-4744302542869753396.pdf-第3页.png

第3页 / 共6页

challenger_yu-10360455-4744302542869753396.pdf-第4页.png

第4页 / 共6页

challenger_yu-10360455-4744302542869753396.pdf-第5页.png

第5页 / 共6页

challenger_yu-10360455-4744302542869753396.pdf-第6页.png

第6页 / 共6页

文本预览

第 33 卷第 1 期 2013 年 1 月 5 日文章编号：0258-8013 (2013) 01-0093-06 中图分类号：TM 71 文献标志码：A 学科分类号：470⋅40 中国电机工程学报 Proceedings of the CSEE Vol.33 No.1 Jan.5, 2013 ©2013 Chin.Soc.for Elec.Eng. 93 基于 RBF 神经网络分位数回归的电力负荷概率密度预测方法何耀耀，许启发，杨善林，余本功 (过程优化与智能决策教育部重点实验室(合肥工业大学)，安徽省合肥市 230009) A Power Load Probability Density Forecasting Method Based on RBF Neural Network Quantile Regression HE Yaoyao, XU Qifa, YANG Shanlin, YU Bengong (Key Laboratory of Process Optimization and Intelligent Decision-making (Hefei University of Technology), Ministry of Education, Hefei 230009, Anhui Province, China) ABSTRACT: According to the problem of short-term load forecasting in the power system, this paper proposed a probability density forecasting method using radical basis function (RBF) neural network quantile regression based on the existed researches on combination forecasting and probability interval prediction. The probability density function of load at any period in a day was evaluated. The proposed method can obtain more useful information than point prediction and interval prediction, and can implement the whole probability distribution forecasting for future load. The practical data of a city in China show that the proposed probability density forecasting method can gain more accurate result of point prediction and obtain the forecasting results of integrated probability density function of short-term load. KEY WORDS: load forecasting; radical basis function (RBF); neural network; quantile regression; probability density function 摘要：针对电力系统短期负荷预测问题，在现有的组合预测和概率性区间预测的基础上，提出了基于 RBF 神经网络分位数回归的概率密度预测方法，得出未来一天中任意时期负荷的概率密度函数，可以得到比点预测和区间预测更多的有用信息,实现了对未来负荷完整概率分布的预测。中国某市实际数据的预测结果表明，提出的概率密度预测方法不仅能基金项目：国家高技术研究发展计划项目(863 计划)(2011AA 05A116)；中国博士后科学基金项目(20100480679，201104323)；全国优秀博士学位作者专项基金(200982)；国家自然科学基金(70901048)。 The National High Technology Research and development of China (863 Program) (2011AA05A116)；China Postdoctoral Science Foundation (20100480679,201104323) ； Author of National Excellent Doctoral Dissertation of P.R. China (200982); National Natural Science Foundation (70901048). 得出较为精确的点预测结果，而且能够获得短期负荷完整的概率密度函数预测结果。关键词：负荷预测；径向基函数；神经网络；分位数回归；概率密度函数 0 引言电力负荷预测是根据电力负荷的过去和现在推测它的未来数值，具有不确定性、条件性、时间性、多方案性等特点。随着现代人工智能方法的快速发展，模糊集、粗糙集、人工神经网络、群体进化算法等智能化方法被广泛引入到电力负荷预测技术之中[1-2]。然而单一的优化方法各自存在一些不足，因此将不同方法组合在一起形成了一些混合预测方法[3]。Amjady 和 Keynia 将小波变换(wavelet transform ， WT) 方法和神经网络进化 (neuro- evolutionary)算法运用到短期负荷预测之中[4]；卫志农等提出了动态状态估计算法与潮流计算相结合的母线超短期负荷预测方法[5]；乔维德、陆宁、周建中、李元诚等分别用粒子群 (particle swarm optimization ，PSO) 算法优化误差反向传播(error backpropagation ， BP) 神经网络 [6] 、径向基函数 (radical basis function ，RBF) 神经网络 [7] 、灰色 Bernoulli 模型[8]和核心向量回归模型[9]的参数； Unsihuay-Vila 等提出了混沌时间序列与进化算法相结合的负荷预测方法[10]；李瑾等利用模拟退火 (simulated annealing ， SA) 算法优化支持向量机 (support vector machine，SVM)中长期负荷预测模型的参数[11]。

94 中国电机工程学报第 33 卷在各种确定性的点预测方法的基础上，从多种不确定性因素出发，开展了大量概率性区间预测的研究工作，给出了一定置信水平下的概率化区间预测结果，可以描述出未来负荷值可能出现的范围[12]。陈新宇等运用序列运算理论得出日极值负荷的概率分布。然而，现有的研究成果都未能给出未来一天中每个时刻电力负荷的完整概率分布函数[13]。回归分析(regression analysis，RA)是确定 2 种或 2 种以上变数间相互依赖的定量关系的一种统计分析方法。已有回归分析通常只关注被响应变量的平均取值，称为均值回归。然而，当响应变量服从非对称分布或者散布较大时，均值回归很难具有代表性。 Koenker 等提出的分位数回归 (quantile regression，QR)可以较好地克服均值回归的不足，能够完整地考察响应变量整个条件分布[14]。许启发等基于分位数回归考察了条件密度预测问题，得到了比均值回归预测更多的有用信息[15]。基于神经网络技术，Taylor 更进一步研究了非线性分位数回归问题，称为神经网络分位数回归，进而给出了条件密度预测方法[16]在神经网络分位数回归的应用情况，Feng 等将其应用于金融市场，解决了金融市场中信用组合投资决策问题[17]；Cannon 等将其应用于环境领域，对降水概率进行了准确预报[18]。本文利用非线性分位数回归理论，建立了短期负荷概率密度分位数回归预测模型，采用标准的梯度优化算法估算出模型的参数向量，运用 RBF 神经网络分位数回归方法给出一天 6 个时段的概率密度函数，选取密度函数的中位数和众数进行误差分析，并与传统的 BP 和 RBF 神经网络的预测结果进行了比较。 1 RBF 神经网络结构 RBF 神经网络是多维空间插值的传统技术，具有很好的全局逼近能力，由输入层、隐含层和输出层组成，是为了克服 BP 神经网络存在的局部最小值和收敛速度慢这 2 个缺陷而提出的神经网络模型，其结构如图 1 所示。作为隐含层基函数的形式，最常用的是高斯核函数： R j ( X c − j ) exp( = − X c − j 2 /2 2 σ j ), 1,2,..., = j p (1) 式中：X=[x1,x2,…,xn]，为 n 维输入向量；cj 为第 j 个基函数的中心，是与 X 具有相同维数的向量；σj 为第 j 个神经元的的标准化常数，即高斯基函数的 x1 x2 xn … Rj(X−cj) w1,1 w1,m w2,1 w2,m … … wj,1 wj,m y1 ym 图 1 RBF 神经网络 Fig. 1 RBF neural network 方差；n、p 分别输入层和隐含层的神经元的个数。确定了隐含层函数后，RBF 网络输入和输出的之间的关系表达式为 y i = p ∑ j 1 = w j i , exp( − x − c j 2 / 2 2 σ j ), i = 1,2,..., m (2) 式中：m 为输出层神经元的个数；yi 为输出层第 i 个神经元的输出值；wj,i 为隐含层第 j 个单元与输出层第 i 个单元之间的连接权值。RBF 神经网络结构的确立，需要求解的参数有 3 个：基函数的数据中心 cj、方差σj 以及隐含层到输出层的权值 wj,i。 RBF 神经网络属于前向型神经网络，其结构具有自适应性，且其输出与初始权值无关。实现 RBF 神经网络的基本思想是用 RBF 作为隐单元的“基” 构成隐藏层空间，隐含层中的基函数对输入信号在局部上产生响应，也就是对输入向量进行变换，将低维的模式数据变换到高维空间中，使得隐含层节点产生较大输出，从而能让在低维空间内的线性不可分的问题在高维空间中线性可分。RBF 网络相比其他前向型网络，具有结构简单、训练简洁、收敛速度快、局部逼近性能好、需设置参数少等特点，因此被广泛应用于非线性优化、时间序列预测和模式识别等科学领域。 2 概率密度负荷预测方法 2.1 分位数回归方法 ( | τ Q = Y ( ) ( ) β τ β τ + 1 0 X ( ) + β τ X ≡ ( ) β τ + 2 1 X β ( ) ′ τ 2 现在考虑一个结果 Y ，受到 k 个因素 X1, X2,…,Xk 的影响，Koenker 等提出了如下的分位数回归模型[14]： X ) X + k k L (3) 式中：QY(τ|X) 为响应变量 Y 在解释变量 X=[X1, X2,…,Xk]′给定下的条件τ分位数；τ∈(0,1)，为分位点；β(τ)=[β0(τ),β1(τ),β2(τ)X2,…,βk(τ)]′，为回归系数向量，随着分位点τ变动，这一点与均值回归分析存在显著差异，在均值回归分析中，回归系数向量

第 1 期何耀耀等：基于 RBF 神经网络分位数回归的电力负荷概率密度预测方法 95 为常数向量。式(3)中参数向量β(τ)的估计，可以转化求解以下优化问题： N Y ( i ∑ τρ min β 1 = i − X ′ β i ∑ (1 i Y | i X ′< i β ) min = β Y i ) τ − Y i − X ′ β i + ∑ τ X ′ ≥ β i X ′ β i i Y | i − (4) 式中：B 为样本量；ρτ(u)=u[τ−I(u<0)]，为检验函数。 I u ( < 0) 1, ⎧ = ⎨ 0, ⎩ u u < ≥ 0 0 (5) 式中 I(⋅)为指示函数，常用的估计方法包括 Koenker 等给出的单纯形法、Portnoy 等给出的内点法[19]等。由式(3)容易看出，在获得参数向量β(τ)估计之后，就能够测算出在不同分位点τ处，解释变量对响应变量的条件分位数的影响。当τ在(0,1)区间上连续取值时，就可以得到响应变量的条件分布，进而得到其条件密度，实现条件密度预测。 2.2 基于 RBF 分位数回归的负荷预测概率密度方法分位数回归模型式(3)采用了线性形式，也就限定了解释变量对响应变量的影响模式为线性范式。然而，更多现实行为表现为非线性范式。人工神经网络能够模拟从输入到输出之间的非线性结构，为解决非线性范式提供了一个有效的工具。基于单隐层神经网络，Taylor 提出了神经网络分位数回归模型[16]： , f [ ) YQ ( | τ =X ( ), ( )] τ τ X W V (6) 式中：W(τ)={wjk(τ)}j=1,2,…,J; k=1,2,…,K，为输入层与隐含层之间的连接权重向量；V(τ)={vj}j=1,2,…,J，为隐含层与输出层之间的连接权重向量；K 为隐含层节点数目；f[X,W(τ),V(τ)]为由权重向量 W(τ)与 V(τ) 复合而成的非线性函数，其表达式为 f [ X W V ( ), ( )] τ τ , J = ∑ g { 2 j 1 = v ( ) τ g 1 [ j K ∑ k 1 = w jk ( ) τ x ki ]} (7) 体现由解释变量 X 到响应变量 Y 的非线性结构。这里，神经网络选取 RBF 神经网络结构，输入层节点直接传递输入信号到隐含层，隐含层节点由高斯核函数式(1)等构成辐射状作用函数 g1(⋅)，输出层节点可以由线性函数 g2(⋅)来转化。特别地，当 g1(⋅) 和 g2(⋅)都是等值函数时，神经网络分位数回归模型式(6)就是线性分位数回归模型。神经网络分位数回归模型式(6)中参数向量 W(τ)、V(τ)的估计可以转化求解优化问题： min{ W V , N ∑ i 1 = Y [ τρ i − f ( X W V , , i )] + λ 1 ∑ ∑ 2 v i } min( = W V , i X W V , , i ∑ ∑ i Y f | ≥ i ( X W V , , i λ 2 f ( f ( w 2 ji + − j i , Y i − ) τ Y i − τ ) (1 ) ) + + ) i X W V , , w + 2 ji i Y | i < f ( λ 1 ∑ j i , X W V , , i λ 2 ∑ i 2 v i ) (8) 式中λ1、λ2 为惩罚参数，以避免网络结构陷入过度拟合的状态。Donaldson 等提出了交叉验证方法[20]，可用于确定惩罚参数λ1、λ2 和隐含层节点数 K 的最优取值。可以使用标准的梯度优化算法对式(8)进行求解，得到参数向量 W(τ)、V(τ)的估计。 , f ( ) ˆ ( ) τ ( ) τ ( | τ ˆ YQ =X ˆ V、 ( ), ( )) τ τ ˆ X W V 在得到参数估计向量 ˆ W 之后，将其分别代入式(4)，就可以得到 Y 的条件分位数估计。 (9) 在获得条件分位数估计之后，可以进一步对条件密度 ˆ ( | YP τ X 进行预测。当τ在(0,1)上连续取值时，分位数曲线 Q 就是分布函数曲线 F，即 F Q 。许启发等[15]由分布函数 F 与分布函数的逆函数 F ( )) τ = τ出发，两边关于τ求微分，推导出之间复合恒等关系 1 1 Q− − 1 F Q ( − F F ( ( )) τ 1 − ) P Q ( ( )) τ = 1 τ τ Q d ( ) / d (10) 对式(10)关于 X 进行条件化和关于τ离散化，即 YP Q τ X 。可得到Y 的条件密度预测 ˆ ˆ( 3 算例仿真 3.1 算例描述 ( ) | ) 本文选取中国某市某年 12 月 7 日至 12 月 19 日的历史电力负荷数据作为算例，以 12 月 7 日至 12 月 17 日为输入数据，12 月 18 日数据为输出数据建立 RBF 神经网络进行网络训练；以 12 月 8 日至 12 月 18 日数据为输入数据，对 12 月 19 日的 24 个时段进行预测。RBF 神经网络的迭代次数为 1 000，神经网络结构为 11-1-1，即输入层的节点数为 11，隐含层为 1，输出层为 1；分位数回归模型的惩罚参数λ1、λ2 都为 1。所有的样本均使用式(11) 进行归一化处理。 X − min X − K (11) X X 1,2, ,24 , X = = t t t max min 式中：Xt 为 t 时刻的样本向量；Xmin、Xmax 分别为所有样本的最小值和最大值。

中国电机工程学报第 33 卷 96 3.2 仿真结果采用 RBF 神经网络分位数回归方法可以得到 12 月 19 日 24 个时段负荷的概率密度曲线，第 1、 5、9、13、17、21 小时的概率密度函数分布区间如图 2 所示。负荷的完整概率分布，且真实值也出现在密度函数之中。同时，可以发现除了第 9 小时的实际值出现在概率密度函数的尾部之外，其余实际值都落在概率密度函数的中部，表明以较高概率出现的电力负荷预测值与实际值几乎相同。在获得了更多信息的同时，为了更好地说明该方法的优势，选取概率密度函数的中位数(即中点)和众数(即密度函数的峰值)的负荷与实际值进行对比，如表 1 所示，中位数和众数的平均绝对误差分别为 1.21%和 1.32%，其最大相对误差分别为 3.822 2%和 3.835 5%。表 1 的计算结果表明，与实际值相比，概率密度函数的中位数和众数的平均绝对误差和最大相对误差十分相近，但是中位数的预测结果更接近实际值。这说明最高概率可能的结果并不一定是最理想的结果。为了充分说明使用 RBF 分位数回归方法的优势，本文列出了 RBF、BP 和 PSO-BP 神经网络的表 1 RBF 分位数回归方法预测结果 Tab. 1 Forecasting results of RBF quantile regression method 时间/h 0:00 1:00 2:00 3:00 4:00 5:00 6:00 7:00 8:00 9:00 10:00 11:00 12:00 13:00 14:00 15:00 16:00 17:00 18:00 19:00 20:00 21:00 22:00 23:00 实际值/ MW 616.223 9 596.241 0 586.304 0 583.484 6 591.235 1 604.175 4 646.088 9 731.201 6 744.928 5 802.489 1 815.600 0 824.319 7 759.681 6 719.229 9 789.486 9 813.171 1 803.750 4 860.330 6 965.051 7 922.696 9 916.377 2 866.874 5 775.147 8 673.879 9 中位数众数预测值/ MW 613.467 7 591.207 0 581.910 3 576.152 2 581.964 4 594.975 2 654.154 1 733.605 9 732.163 2 784.717 3 806.065 0 820.259 7 762.855 7 719.971 7 781.091 8 796.118 9 793.755 5 851.151 0 928.165 8 911.928 3 908.328 1 880.786 9 788.299 3 676.464 7 MW 预测值/ 相对误差/% −0.447 3 613.355 9 −0.844 3 591.436 0 −0.749 4 583.034 8 −1.256 7 576.922 3 −1.568 0 583.010 0 −1.522 8 594.707 6 1.248 3 654.345 3 0.328 8 731.998 9 −1.713 6 721.017 8 −2.214 6 778.922 4 −1.169 1 803.910 1 −0.492 5 818.360 9 0.417 8 757.899 2 0.103 1 718.784 7 −1.063 4 778.758 8 −2.097 0 794.595 3 −1.243 5 793.379 7 −1.067 0 848.169 3 −3.822 2 928.037 4 −1.167 1 929.738 1 −0.878 4 926.500 8 1.604 9 881.671 1 1.696 6 785.527 5 0.383 6 677.757 1 相对误差/% −0.465 4 −0.805 9 −0.557 6 −1.124 7 −1.391 2 −1.567 1 1.277 9 0.109 0 −3.209 8 −2.936 7 −1.433 3 −0.722 9 −0.234 6 −0.061 9 −1.358 9 −2.284 4 −1.290 3 −1.413 6 −3.835 5 0.763 1 1.104 7 1.706 9 1.339 1 0.575 4 度密率概 0.04 0.02 0.00 度密率概 0.08 0.04 0.00 0.03 度 0.02 密率 0.01 概 0.00 实际值 600 620 640 电力负荷/MW (a) 第 1 小时实际值 570 580 590 600 电力负荷/MW (b) 第 5 小时 610 620 实际值 680 700 720 电力负荷/MW (c) 第 9 小时 740 0.04 度密率概 0.02 0.00 730 度密率概 0.03 0.02 0.01 0.00 0.04 度密率概 0.02 0.00 实际值 750 770 电力负荷/MW (d) 第 13 小时 790 实际值 760 780 800 820 840 860 电力负荷/MW (e) 第 17 小时实际值 890 900 910 920 电力负荷/MW (f) 第 21 小时 930 940 图 2 概率密度函数图 Fig. 2 Diagram of probability density function 从图 2 的 6 个时段的概率密度函数的预测结果可以看出，使用 RBF 分位数回归方法可以得到未来

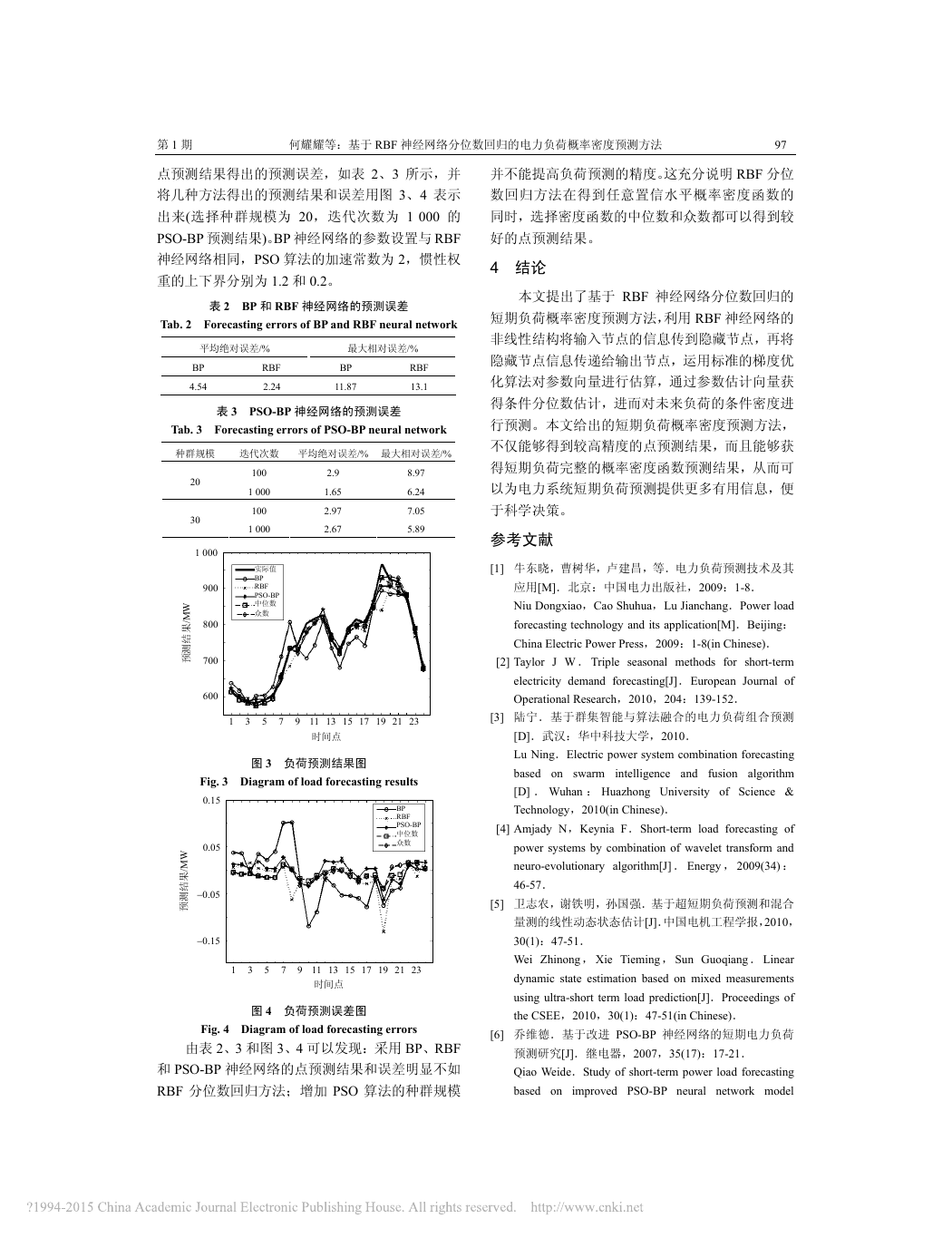
第 1 期何耀耀等：基于 RBF 神经网络分位数回归的电力负荷概率密度预测方法 97 点预测结果得出的预测误差，如表 2、3 所示，并将几种方法得出的预测结果和误差用图 3、4 表示出来(选择种群规模为 20，迭代次数为 1 000 的 PSO-BP 预测结果)。BP 神经网络的参数设置与 RBF 神经网络相同，PSO 算法的加速常数为 2，惯性权重的上下界分别为 1.2 和 0.2。表 2 BP 和 RBF 神经网络的预测误差 Tab. 2 Forecasting errors of BP and RBF neural network 平均绝对误差/% 最大相对误差/% BP 4.54 RBF 2.24 BP 11.87 RBF 13.1 表 3 PSO-BP 神经网络的预测误差 Tab. 3 Forecasting errors of PSO-BP neural network 种群规模迭代次数平均绝对误差/% 最大相对误差/% 2.9 1.65 2.97 2.67 8.97 6.24 7.05 5.89 100 1 000 100 1 000 实际值 BP RBF PSO-BP 中位数众数 20 30 1 000 / W M 果结测预 900 800 700 600 1 3 5 7 9 15 11 13 时间点 17 19 21 23 图 3 负荷预测结果图 Fig. 3 Diagram of load forecasting results 0.15 BP RBF PSO-BP 中位数众数 / W M 果结测预 0.05 −0.05 −0.15 1 3 5 7 9 15 11 13 时间点 17 19 21 23 图 4 负荷预测误差图 Fig. 4 Diagram of load forecasting errors 由表 2、3 和图 3、4 可以发现：采用 BP、RBF 和 PSO-BP 神经网络的点预测结果和误差明显不如 RBF 分位数回归方法；增加 PSO 算法的种群规模并不能提高负荷预测的精度。这充分说明 RBF 分位数回归方法在得到任意置信水平概率密度函数的同时，选择密度函数的中位数和众数都可以得到较好的点预测结果。 4 结论本文提出了基于 RBF 神经网络分位数回归的短期负荷概率密度预测方法，利用 RBF 神经网络的非线性结构将输入节点的信息传到隐藏节点，再将隐藏节点信息传递给输出节点，运用标准的梯度优化算法对参数向量进行估算，通过参数估计向量获得条件分位数估计，进而对未来负荷的条件密度进行预测。本文给出的短期负荷概率密度预测方法，不仅能够得到较高精度的点预测结果，而且能够获得短期负荷完整的概率密度函数预测结果，从而可以为电力系统短期负荷预测提供更多有用信息，便于科学决策。参考文献 [1] 牛东晓，曹树华，卢建昌，等．电力负荷预测技术及其应用[M]．北京：中国电力出版社，2009：1-8． Niu Dongxiao，Cao Shuhua，Lu Jianchang．Power load forecasting technology and its application[M]．Beijing： China Electric Power Press，2009：1-8(in Chinese)． [2] Taylor J W ． Triple seasonal methods for short-term electricity demand forecasting[J]．European Journal of Operational Research，2010，204：139-152． [3] 陆宁．基于群集智能与算法融合的电力负荷组合预测 [D]．武汉：华中科技大学，2010． Lu Ning．Electric power system combination forecasting based on swarm intelligence and fusion algorithm [D] ． Wuhan ： Huazhong University of Science & Technology，2010(in Chinese)． [4] Amjady N，Keynia F．Short-term load forecasting of power systems by combination of wavelet transform and neuro-evolutionary algorithm[J] ． Energy ， 2009(34) ： 46-57． [5] 卫志农，谢铁明，孙国强．基于超短期负荷预测和混合量测的线性动态状态估计[J]．中国电机工程学报，2010， 30(1)：47-51． Wei Zhinong ， Xie Tieming ， Sun Guoqiang ． Linear dynamic state estimation based on mixed measurements using ultra-short term load prediction[J]．Proceedings of the CSEE，2010，30(1)：47-51(in Chinese)． [6] 乔维德．基于改进 PSO-BP 神经网络的短期电力负荷预测研究[J]．继电器，2007，35(17)：17-21． Qiao Weide．Study of short-term power load forecasting based on improved PSO-BP neural network model

98 中国电机工程学报第 33 卷 [J]．Relay，2007，35(17)：17-21(in Chinese)． 64-72(in Chinese)． [7] 陆宁，周建中，何耀耀．粒子群优化的神经网络模型在短期负荷预测中的应用[J]．电力系统保护与控制，2010， 38(12)：65-68． Lu Ning，Zhou Jianzhong，He Yaoyao．Particle swarm optimization-based neural network model for short-term load forecasting[J] ． Power System Protection and Control，2010，38(12)：65-68(in Chinese)． [8] Zhou J Z，Fang R C，Li Y H，et al．Parameter optimization of nonlinear grey Bernoulli model using particle swarm optimization[J]．Applied Mathematics and Computation， 2009(207)：292-299． [9] 李元诚，刘克文．面向大规模样本的核心向量回归电力负荷快速预测方法[J]．中国电机工程学报，2010， 30(28)：18-22． Li Yuancheng ， Liu Kewen ． A rapid electric load forecasting method using core vector regression for large scale data set[J]．Proceedings of the CSEE，2010，30(28)： 18-22(in Chinese)． [10] Unsihuay-Vila C，Zambroni de S A C，Marangon- Lima J W，et al．Electricity demand and spot price forecasting using evolutionary computation combined with chaotic nonlinear dynamic model[J]．Electrical Power and Energy Systems，2010(32)：108-116． [11] 李瑾，刘金朋，王建军．采用支持向量机和模拟退火算法的中长期负荷预测方法[J]．中国电机工程学报，2011， 31(16)：63-66． Li Jin，Liu Jinpeng，Wang Jianjun．Mid-long term load forecasting based on simulated annealing and SVM algorithm[J]．Proceedings of the CSEE，2011，31(16)： 63-66(in Chinese)． [12] 方仍存．电力系统负荷区间预测[D]．武汉：华中科技大学，2008． Fang Rengcun．Power system load interval forecasting [D] ． Wuhan ： Huazhong University of Science & Technology，2008(in Chinese)． [13] 陈新宇，康重庆，陈敏杰．极值负荷及其出现时刻的概率化预测[J]．中国电机工程学报，2011，31(22)：64-72． Chen Xinyu，Kang Chongqing，Chen Minjie．Short term probabilistic forecasting of the magnitude and timing of extreme load[J]．Proceedings of the CSEE，2011，31(22)： [14] Koenker R W ， Bassett J G ． Regression quantiles [J]．Econometrica，1978，46(1)：33-50． [15] 许启发，蒋翠侠．分位数局部调整模型及应用[J]．数量经济技术经济研究，2011，28(8)：115-133． Xu Qifa，Jiang Cuixia．Quantile partial adjustment model and its application[J]．Journal of Quantitative & Technical Economics，2011，28(8)：115-133(in Chinese)． [16] Taylor J W ． A quantile regression neural network approach the conditional density of multiperiod returns[J]．Journal of Forecasting，2000， 19(4)：299-311． to estimating [17] Feng Y，Li R，Sudjianto A，et al．Robust neural network to credit portfolio data analysis with applications [J]．Statistics and Its Interface，2010，3(4)：437． [18] Cannon A J ． Quantile regression neural networks ： implementation in R and application to precipitation downscaling[J]．Computers & Geosciences，2010，37(9)： 1277-1284． [19] Portnoy S ，Koenker R ．The Gaussian hare and the Laplacian tortoise：computability of squared-error versus absolute-error estimators[J]．Statistical Science，1997， 12(4)：279-300． [20] Donaldson R G，Kamstra M．Forecast combining with neural networks[J]．Journal of Forecasting，1996，15(1)： 49-61．何耀耀收稿日期：2012-05-14。作者简介：何耀耀(1982)，男，工学博士，讲师，硕士生导师，主要从事智能优化方法在电力系统中的应用，hy-342501y@163.com；许启发(1975)，男，教授，博士生导师，主要从事分位数回归理论与方法研究， xuqifa1975@163.com；杨善林(1948)，男，教授，博士生导师，研究方向为人工智能、决策科学与技术， hgdysl@gmail.com。 (责任编辑刘浩芳)

分享到：

赞收藏

资料库

基于RBF 神经网络分位数回归的概率密度预测方法.pdf

相关推荐

行业

热门标签

最新资料