Computer Engineering and Applications 计算机工程与应用 2012，48（22） 41 ⦾ ⦾ 研究、探讨 多重网格方法求解两类 Helmholtz 方程 赵 婧，聂玉峰 ZHAO Jing, NIE Yufeng 西北工业大学 应用数学系，西安 710129 Department of Applied Mathematics, Northwestern Polytechnical University, Xi’an 710129, China ZHAO Jing, NIE Yufeng. Multigrid method applied to two kinds of Helmholtz equations. Computer Engi- neering and Applications, 2012, 48（22）：41-44. Abstract：The procedure of multigrid method is described in detail and its properties are discussed by applying mul- tigrid to both positive definite Helmholtz equation and indefinite Helmholtz equation. Comparisons of convergence performance are implemented between V cycle, W cycle and F cycle. It is shown that, by solving positive definite Helmholtz equation, multigrid method has high computing efficiency. However, as the value of wave-number in- creases in indefinite Helmholtz equation, the results obtained by multigrid method diverge. The reasons lie in both fine grid smoothing and coarse grid correction, and the improvement of Multigrid is still needed in future. Key words：multigrid; F cycle; positive definite Helmholtz; indefinite Helmholtz 摘 要：详细给出了多重网格方法的实现过程，借助正定 Helmholtz 方程及不定 Helmholtz 方程的求解来探讨多 重网格方法的特性。对多重网格 V 环、W 环以及 F 环三种不同迭代格式的收敛效果进行了对比。通过正定 Helmholtz 方程的求解，发现多重网格的确有很高的计算效率。对于不定 Helmholtz 方程，随着波数的增加，利 用多重网格方法得到结果不收敛，原因出在细网格光滑和粗网格矫正过程。如何针对此问题对多重网格进行 有效改进还有待进一步研究。 关键词：多重网格；F 环；正定 Holmholtz 方程；不定 Helmholtz 方程 文章编号：1002-8331（2012）22-0041-04 文献标识码：A 中图分类号：TP301.6 1 引言 多重网格方法的基本思想来源于套迭代（nested iteration）、松弛方法的误差光滑以及总下降（total reduction）。 自 从 上 世 纪 60 年 代 Fedorenko[1-2] 和 Bakhvalov[3]第一次提出严格意义上的多重网格方法 以来，众多学者对此方法进行了多方面的研究。Brandt 于上世纪 70 年代从理论上证明了多重网格方法的可 靠性，并且介绍了非线性多重网格方法（FAS），自适 应技术（MLAT）[4]以及用于误差分析的局部傅里叶分 析方法[5]。此后，如何将多重网格方法推广到更一般 的计算区域，如何将其与有限单元法、有限差分法以 及有限容积法相结合以及它的自适应性、并行性等 研究课题也取得了众多发展[5]。 本文首先详细给出了多重网格的实现过程，然 后利用多重网格方法分别对正定 Helmholtz 方程及不 定 Helmholtz 方程进行求解，其中对比讨论了 V 环，W 环以及 F 环三种不同迭代格式的收敛效果。最后，对 于多重网格方法在求解不定 Helmholtz 方程时失效的 基金项目：国家自然科学基金项目（No.90916027，No.11071196）。 作者简介：赵婧（1986—），女，硕士研究生，主要研究领域为多重网格方法及其工程应用；聂玉峰（1968—），男，通讯作者，博士，教授。 E-mail：jejin128@gmail.com 收稿日期：2011-08-03 修回日期：2011-11-04 DOI：10.3778/j.issn.1002-8331.2012.22.008 CNKI 出版日期：2011-12-09 http://www.cnki.net/kcms/detail/11.2127.TP.20111209.1003.073.html 

42 2012，48（22） Computer Engineering and Applications 计算机工程与应用 原因进行了分析。 2 二重网格方法 一个基本的多重网格法由两部分组成：细网格 光滑和粗网格校正。这里从基本的二重网格开始阐 述，然后拓展到多重网格。在此，考虑如下形式的二 维线性椭圆边值问题： Lu(xy)= f (xy) in (xy)Î Ω LΓ u(xy) = g(xy) on (xy)Î Γ: = ¶Ω ì í î （1） 其中，LLΓ 是算子，Ω Ì R2 是求解区域，Γ 是区域 边界。通过对问题（1）进行离散（例如可用 5 点差分 格式），得到如下的离散方程组： h h (xy) (xy)Î Ω (xy) = f h 是 L 的离散算子，f （2） u L h 其中，L 是 f 限制到网格点上 的值，下角标 h 代表网格尺寸。这里假设此问题有 解。针对问题（2）的二重网格算法具体阐述如下。 2.1 前细网格光滑（pre-smoothing） h 离散方程组（2）可以采用 Gauss-Seidel，Jacobi 等 的一个近 方法求解，经过迭代得到式（2）的精确解 u 似解 uˉ m h vm h ，此时的误差 vm h : = u 定义为： - uˉ m h h h （3） (x + hy + h) + d (x - hy + h) + d d d h h h h (x + hy - h) + (x - hy - h)] （5） 综合式（3）、（4），得到粗网格上的残量方程： L 在粗网格上求解方程（6），得到解 v̂ m H （6） 。然后利用 = dˉ m H v̂ m H H 从粗网格传送回细网格： 插值算子 I h 将解 v̂ m H H = I h v̂ m H H v̂ m h 对于算子 I h H （7） ，以单元尺寸由 2h 到 h 的网格为 例，给出一个常用的插值算子，如图 2 及式（8）所示： for ● ì vm ï 2h ï 1 ï [vm ïï 2 2h ï 1 í 2 ï ï 1 ï ïï 4 ï vm î 2h [vm 2h (xy + h) + vm 2h (x + hy) + vm 2h (xy - h)] for  (x - hy)] for ⋄ （8） I h 2h vm 2h = (x + hy + h) + vm 2h (x - hy - h)] for  [vm 2h (x - hy + h) + vm 2h (x + hy - h) + 其中，上角标 m 表示多重网格迭代的次数。 2.2 粗网格校正（Coarse Grid Correction，CGC） 2h ，首先计算残量 dˉ m h ： 利用逼近解 uˉ m h dˉ m uˉ m h h 然后利用算子 I H h : = f - L h h （4） ，将细网格上的残量限制传送 2h 图 2 双线性插值 到粗网格上，如图 1 所示。 Ωh Ω2h 图 1 粗网格到细网格的投影算子 得到 v̂ m h 之后，对之前在细网格上得到的逼近解 进行校正： uˉ m h umafterCGC h = uˉ m h + v̂ m h 2.3 后细网格光滑（Post-smoothing） 这里对经过粗网格校正得到的解 umafterCGC h （9） 再次 进行光滑，由此得到新的迭代步上的解 um + 1 。至此， 一个完整的二重网格迭代就完成了。用图 3 更直观 地表示了这一过程： h um h uˉ m h dˉ m h = f h - L uˉ m h h v̂ m h uˉ m h + v̂ m h 细网格 um + 1 h 这里上下角标 H 和 h 分别代表粗细网格的单元 ，以单元尺寸由 h 到 2h 的网格为 尺寸。对于算子 I H h 例，常用如下完全权算子（full weighting operator）： I H h dˉ m H I h H L v̂ m H H = dˉ m H 图 3 二重网格过程 粗网格 d 2h (xy) = I 2h h 2d 2d h h (xy) = 1 d 16 h (x - hy) + 2d (xy + h) + 2d [4d h (xy) + (x - hy) + (xy - h) + h h 2.4 多重网格 如果在粗网格上不直接精确求解残量方程（6）， 而是继续利用新的二重网格法来逼近残量方程的 

赵 婧，聂玉峰：多重网格方法求解两类 Helmholtz 方程 2012，48（22） 43 解，便得到了多重网格结构，如图 4 所示。其中，γ 表 示多重网格在粗网格上应用的次数，●表示细网格光 滑，○表示求解精确解，\表示细网格到粗网格的传 送，/表示粗网格到细网格的传送。 二重网格： 三重网格： 四重网格： γ=1 γ=2 γ=1 γ=2 五重网格： γ=2 图 4 多重网格结构 l=1 l=2 l=3 l=4 衡量收敛速度，而 q̂ (m) 表示迭代 m 次后残量减少的平 均值。当 m 值较大的时，q̂ (m) 可以给出一个较好的估计。 3 算例结果与分析 Helmholtz 方程是一个描述电磁波的椭圆偏微分 方程，常出现在物理学中的电磁辐射、地震学和声学 等领域的问题中。这里，首先利用多重网格方法求 解正定 Helmholtz 方程，由此检测多重网格方法的有 效性。然后，利用同样方法求解不定 Helmholtz 方程。 3.1 算例一：正定 Helmholtz 方程 考虑二维情况 ì -Ñ2u(xy) + k 2u(xy) = ïï -2y3 - 6x2 y + k 2 x2 y3 in Ω =[01]´[01] í ïï u(xy) = x2 y3 on ¶Ω î （10） 其 中 ，k 是 波 数 ，u 是 振 幅 。 此 问 题 的 解 析 解 为 (xy) = x2 y3 。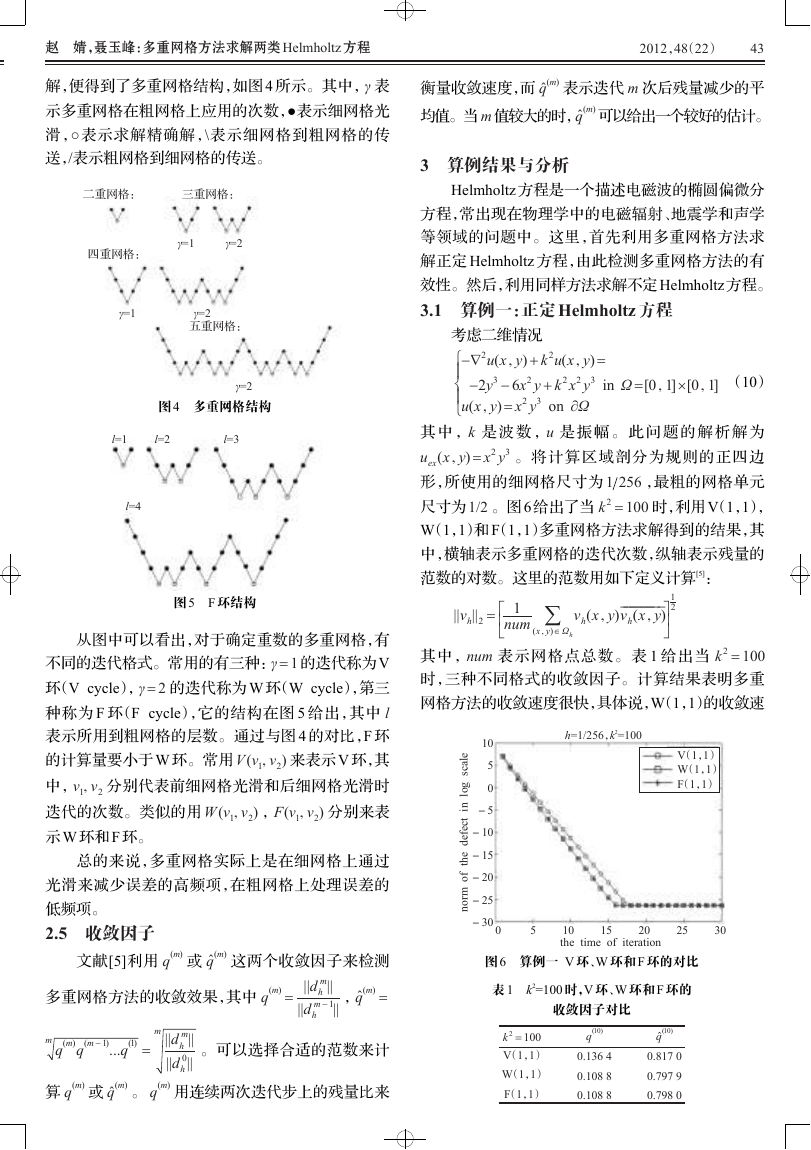将计算区域剖分为规则的正四边 u ex 形，所使用的细网格尺寸为 1 256 ，最粗的网格单元 尺寸为 1/2 。图 6 给出了当 k 2 = 100 时，利用 V（1，1）， W（1，1）和 F（1，1）多重网格方法求解得到的结果，其 中，横轴表示多重网格的迭代次数，纵轴表示残量的 范数的对数。这里的范数用如下定义计算[5]： 图 5 F 环结构 ||v || h 2 1 num å = é ê ë (xy)Î Ω (xy) v h h 1 2 -- --- -- - - - ù (xy) v ú h û 从图中可以看出，对于确定重数的多重网格，有 不同的迭代格式。常用的有三种：γ = 1 的迭代称为 V 环（V cycle），γ = 2 的迭代称为 W 环（W cycle），第三 种称为 F 环（F cycle），它的结构在图 5 给出，其中 l 表示所用到粗网格的层数。通过与图 4 的对比，F 环 ν 的计算量要小于 W 环。常用 V (ν ) 来表示 V 环，其 1 ν 分别代表前细网格光滑和后细网格光滑时 中，ν 1 ν 迭代的次数。类似的用 W (ν ) 分别来表 1 示 W 环和 F 环。 ν ) ，F(ν 1 2 2 2 2 总的来说，多重网格实际上是在细网格上通过 光滑来减少误差的高频项，在粗网格上处理误差的 低频项。 2.5 收敛因子 其中，num 表示网格点总数。表 1 给出当 k 2 = 100 时，三种不同格式的收敛因子。计算结果表明多重 网格方法的收敛速度很快，具体说，W（1，1）的收敛速 10 5 0 －5 －10 －15 －20 －25 －30 e l a c s g o l n i t c e f e d e h t f o m r o n 0 5 h=1/256，k2=100 10 the time of iteration 15 20 V（1，1） W（1，1） F（1，1） 25 30 文献[5]利用 q(m) 或 q̂ (m) 这两个收敛因子来检测 图 6 算例一 V 环、W 环和 F 环的对比 多重网格方法的收敛效果，其中 q(m) = ||d m || h ||d m - 1 || h ，q̂ (m) = m q(m)q(m - 1)...q(1) = m ||d m || h ||d 0 || h 。可以选择合适的范数来计 算 q(m) 或 q̂ (m) 。 q(m) 用连续两次迭代步上的残量比来 表 1 k2=100 时，V 环、W 环和 F 环的 收敛因子对比 k 2 = 100 V（1，1） W（1，1） F（1，1） q(10) 0.136 4 0.108 8 0.108 8 q̂ (10) 0.817 0 0.797 9 0.798 0 

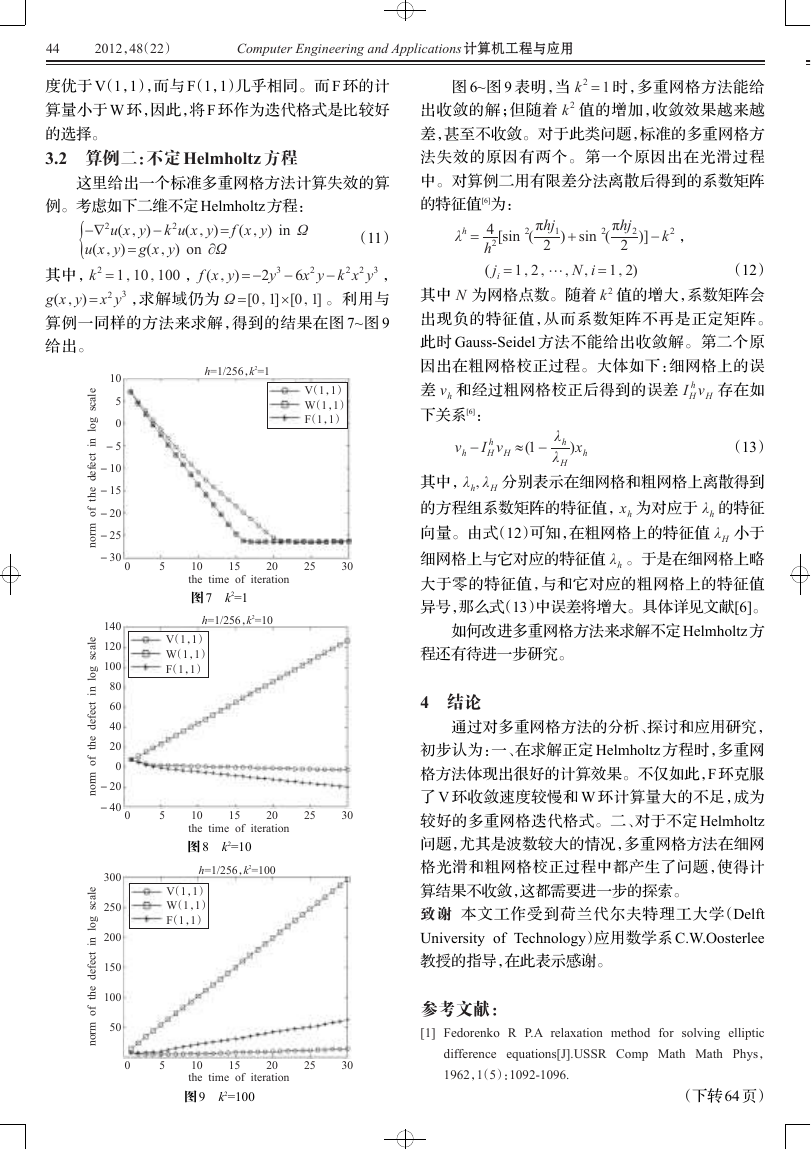
44 2012，48（22） Computer Engineering and Applications 计算机工程与应用 度优于 V（1，1），而与 F（1，1）几乎相同。而 F 环的计 算量小于 W 环，因此，将 F 环作为迭代格式是比较好 的选择。 3.2 算例二：不定 Helmholtz 方程 这里给出一个标准多重网格方法计算失效的算 例。考虑如下二维不定 Helmholtz 方程： {-Ñ2u(xy) - k 2u(xy) = f (xy) in Ω u(xy) = g(xy) on ¶Ω （11） 其中，k 2 = 110100 ，f (xy) = -2y3 - 6x2 y - k 2 x2 y3 ， g(xy) = x2 y3 ，求解域仍为 Ω =[01]´[01] 。利用与 算例一同样的方法来求解，得到的结果在图 7~图 9 给出。 10 5 0 －5 －10 －15 －20 －25 －30 140 120 100 80 60 40 20 0 －20 －40 300 250 200 150 100 50 e l a c s g o l n i t c e f e d e h t f o m r o n e l a c s g o l n i t c e f e d e h t f o m r o n e l a c s g o l n i t c e f e d e h t f o m r o n 0 5 0 5 0 5 h=1/256，k2=1 V（1，1） W（1，1） F（1，1） 20 15 10 the time of iteration 图 7 k2=1 h=1/256，k2=10 V（1，1） W（1，1） F（1，1） 20 15 10 the time of iteration 图 8 k2=10 h=1/256，k2=100 V（1，1） W（1，1） F（1，1） 20 15 10 the time of iteration 图 9 k2=100 25 30 25 30 25 30 图 6~图 9 表明，当 k 2 = 1 时，多重网格方法能给 出收敛的解；但随着 k 2 值的增加，收敛效果越来越 差，甚至不收敛。对于此类问题，标准的多重网格方 法失效的原因有两个。第一个原因出在光滑过程 中。对算例二用有限差分法离散后得到的系数矩阵 的特征值[6]为： λh = 4 h2 ( j [sin 2( πhj 1 2 ) + sin 2( πhj 2 = 12Ni = 12) 2 )] - k 2 ， i （12） 其中 N 为网格点数。随着 k 2 值的增大，系数矩阵会 出现负的特征值，从而系数矩阵不再是正定矩阵。 此时 Gauss-Seidel 方法不能给出收敛解。第二个原 因出在粗网格校正过程。大体如下：细网格上的误 差 v 存在如 下关系[6]： 和经过粗网格校正后得到的误差 I h H v H h v h - I h H v H »(1 - λ λ H h )x h （13） h H λ h 为对应于 λ 其中，λ 分别表示在细网格和粗网格上离散得到 的方程组系数矩阵的特征值，x 的特征 h 向量。由式（12）可知，在粗网格上的特征值 λ 小于 细网格上与它对应的特征值 λ 。于是在细网格上略 大于零的特征值，与和它对应的粗网格上的特征值 异号，那么式（13）中误差将增大。具体详见文献[6]。 如何改进多重网格方法来求解不定 Helmholtz 方 H h 程还有待进一步研究。 4 结论 通过对多重网格方法的分析、探讨和应用研究， 初步认为：一、在求解正定 Helmholtz 方程时，多重网 格方法体现出很好的计算效果。不仅如此，F 环克服 了 V 环收敛速度较慢和 W 环计算量大的不足，成为 较好的多重网格迭代格式。二、对于不定 Helmholtz 问题，尤其是波数较大的情况，多重网格方法在细网 格光滑和粗网格校正过程中都产生了问题，使得计 算结果不收敛，这都需要进一步的探索。 致谢 本文工作受到荷兰代尔夫特理工大学（Delft University of Technology）应用数学系 C.W.Oosterlee 教授的指导，在此表示感谢。 参考文献： [1] Fedorenko R P.A relaxation method for solving elliptic difference equations[J].USSR Comp Math Math Phys， 1962，1（5）：1092-1096. （下转 64 页）