第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
信噪比估计算法研究.pdf
0535
0536
0537
0538
0539
0540
0541
0542
0543
第 12 卷第 5 期
2011 年 10 月
信息工程大学学报
Journal of Information Engineering University
Vol. 12 No.5
Oct. 2011
信噪比估计算法研究
张金成 1 ，彭 华 1 ，赵国庆 1 ,2
(1.信息工程大学信息工程学院，河南郑州 450002; 2.72406 部队，山东威海 264200)
摘要:信噪比是现代无线通信系统中的重要参数之一，人们对信噪比估计技术进行了大量的研
究。根据所采用的信号处理技术不同，分最大似然、谱分析和基于统计量等 3 类基本的信噪比
估计方法，并给出了典型估计方法的比较和计算机仿真，得到了一些较为直观的结论。最大似
然方法精度高，但需要周期地发送训练序列;谱分析方法实现简单，但估计精度有限;基于统计
量的方法需要较大的数据量才能实现信噪比的精确估计。
关键词:信噪比估计;无线通信;最大似然;谱分析;统计量
中图分类号 :TN91 1. 6
文献标识码 :A
文章编号 :1671 -0673(2011)05 -0535 -09
Research 00 SNR Estimatioo Algorithms
ZHANG Jin-cheng
1 , PENG Hua
1 , ZHAO Guo-qing
1
.
2
( 1. Institute of Information Engineering , Information Engineering University , Zhengzhou 450002 , China;
2. U nit 72406 , Weihai 264200 , China)
Abstract: Signal to noise ratio (SNR) is a key parameter in modern wireless communication sys
tems. and SNR estimation attracts the attention of many researchers. In this paper. several SNR es
timation methods proposed recently are presented. with typical estimation methods simulated and
compared. and then some conclusions are drawn. The ML methods are accurate buther training se
quences have to be sent periodically. Spectrum analysis methods can be easily implemented. but the
performance is poor. Statistics-based methods reguire large amounts of data to realize precise estima
tion.
Key words: SNR estimation; wireless communication; ML; spectrum analysis; statistics
0 引言
信噪比信息在自适应系统和类 Turbo( 包括类 Turbo 码、迭代比特交织调制编码以及 Turbo 均衡等)系
统中非常重要，精确估计对保证这些系统逼近理想性能具有非常重要的意义[ 1] 。如码分多址系统中利用
信噪比信息进行各链路的功率分配;自适应调制系统根据信噪比来选择调制方式或编码速率;在 Turbo 类
选代译码器译码初始化步骤中，需要准确的信噪比参数以生成接收比特的先验信息 [2]; 在块传输 (OFDM
和 SC-FDE) 系统的 MMSE 均衡中，也需要根据精确的信噪比信息设计相应的频域均衡器，以提高系统的
可靠性 [34] 。
信噪比信息不仅对许多算法本身很重要，而且为很多信号处理过程提供了关键的参考信息。如均衡
收稿日期: 20 1I '{)3 -28 ;修回日期 :20 1l '{)8-22
基金项目:国家自然科学基金资助项目 (61072046)
作者简介:张金成 (1984-). 男，硕士生，主要研究方向为双选信道估计与信噪比估计。
536
信息工程大学学报
2011 年
处理中，在盲均衡算法与判决指向 (DD) 算法切换时机的选择上，最可靠的依据就是信噪比 [5] 。此外，通
过估计输入判决器信号的信噪比，可以粗略知道信号的解调质量水平，这是由于此时信号信噪比可以方便
地对应到误码率和解调性能上去[ 6 ]。信噪比作为现代通信系统中的一个重要参数，人们对其估计技术进
行了广泛的研究。本文就近年来常用的信噪比估计技术进行了系统阐述，给出了典型估计方法的仿真，在
此基础上得到了一些相对直观的结论，为信噪比估计方法在实际中的应用提供了重要的参考信息。
1 系统模型
为了便于比较各算法的性能，本文采用图 1 所示的等效数字通信系统模型。
信号源 d斗过采祥 μi
采样
I z,
高斯自噪声 E
J万
成型滤波
h,
J言
m,
e i屿，
图 1 等效数字通信系统模型
k=nN"
yk
Y.
匹配滤波
图 1 中，叽为映射后信号，满足 E{an1 α n2} = u:8(n 1
， hk 为成型滤波器系数 ， N" 为每符号的采样
点数。当 wc=O 时，图 l 所示为等效基带系统模型;当 W ， 并 O 时，图 1 所示为等效带通系统模型。需要说明
的是，当飞为 BPSK 信号时，考虑实高斯白噪声信道;当 αn 为 QPSK 等复信号时，考虑复高斯白噪声信道。
- n2 )
过采样和脉冲成型后的信号可表示为
则接收信号可表示为
m k = 2, α n h川，
-
-
且
、
‘E
F
，
，
，
、
(2)
式中 ， Zk 是零均值单位方差加性高斯白噪声， S 是信号功率因子 ， N 是噪声功率因子。则匹配滤波输出信号
为
rk = ßm k + 厅Zk
Yk = (♂mk + 厅Zk) @凡=♂ plmkJ+J万平ZZk_Z
式中，@代表离散卷积， *表示共辄。最后对匹配滤波器输出信号下采样，得
式中， gιk = hιk ③ hι丁k= 车 hZhk_Z ， wn = Yk I k 叫
y几n=叮Y k I 山I k = n耐N.. =，j♂Eαπngo品o+J厅万w
(3)
(4)
2 主要的信噪比估计算法
根据是否需要训练序列，信噪比估计算法可以分为有数据辅助 (DA) 和非数据辅助( NDA)2 类。本文
从采用的信号处理方法的角度出发，将信噪比估计方法分为基于最大似然 (ML) 、基于谱分析和基于统计
量等 3 类。
2. 1 基于最大似然的估计方法
基于 ML 的信噪比估计算法中，所用信号既有输入匹配滤波器的过采样信号 rk ， 也有输入判决器的符
号间隔采样信号 Yn O 文献 [7] 研究了过采样信号的信噪比估计问题，推导得到了 MPSK 信号在复 AWGN 信
道条件下的估计器:
时， [运 Re{川r
PML , DA , Complex =
• r- l
~~ Irk l 2 叫[去 ZRef机 }r
_ K-l
?
(5)
第 5 期
张金成等:信噪比估计算法研究
537
其中，下标‘ DA' 表示数据辅助 ;K 为用于估计的样点数，‘* '表示共辄运算， Re{.} 表示取大括号内数据
的实部。对实信号通过实信道的情形，通过将上式中的复数成份改成相应的实数即可。
为进一步提高估计器的性能，文献 [7J 给出了实 AWGN 和复 AWGN 信道下的低偏差信噪比估计器:
PML , DA ,æal
-
PML , DA.Complex
N;, [ 过门mk]
lL IMK I
Zd- 讨元[三叫 2
叫过 Re{川f
lZ !rJ-KK-ss3AJ ER叫 mk } ]
K-I
I\T
(6)
(7)
即在 (5) 式的基础上，分母分别乘以一个因子 K/(K - 3) 和 K/(K - 3/2) 。
从 (5) - (7) 式不难看出，过采样条件下基于 ML 的信噪比估计器需要知道成型滤波器输出信号，是
DA 类算法。若将该类算法推广到非协作通信中，使之成为 NDA 类算法，那么不仅需要准确估计发送符号，
而且还要知道成型滤波器系数，以便重构叫，从而给信噪比估计带来了双重困难，极大限制了 NDA 类方
法在实际中的应用。
通过前面分析易知， ML 类算法难以推广到非协作通信下的过采样信号的信噪比估计当中。因此，对
ML 类非数据辅助算法来说，其估计用信号主要是输入判决器的符号间隔采样信号凡，可认为已经基本消
除了载波偏差和码间干扰，仅有 AWGN 的影响。此时，该估计器通常又称为信号平方比噪声方差 (SNV) 估
计器，由 (6) - (7) 式易得
PSNV , DA , reø.1 =
li:?αnf
(NL亏了Xyi-N(ι3)[XYnα] 2
I 去主 Re句:αJl2
PSNV. DA , complex =
s 17772|yJL 川 LM)[ 主叫时f
(8)
(9)
N， 为用于估计的样点数。
由 (8) 、 (9) 式知，以上 2 个估计器均需要知道发送符号信息，是 DA 类算法。若利用发送符号的估计ι
代替叽，则得到 NDA 类估计器:
PSNV , NDA , æal
-
PSNV. NDA , compJex
[ ~，主叭r
(Ns!士亏了三 y:-N( 」 -3)[ 主川nf
lt主 Re川 ωr
、-丁、N盯(NιL ωω[非呈岸Re叫e
1-丁丁工丁7工丁丁丁÷E;扣|川了 |M2LV
(1 0)
J
'
t飞
4EA
咽
'
-
、
1
/
在数据辅助条件下， ML 类算法是最优的，其估计效果接近克拉米罗下限 (ωC l1L山B) ;但在没有数据辅助
时，其估计效果在高信噪比下较好，低信噪比下由于判决误差影响，其性能很差。为了提高 ML 类 NDA 算法
在低信噪比下的估计性能，文献 [5 ， 7J 将对 MPSK 信号的信噪比估计问题转化为对发送符号的幅值估计，
提出了一系列有效降低判决错误的改进算法。文献 [8J 提出了一种基于迭代的信号幅度和信噪比联合估
计算法，改善了由判决错误导致的估计偏差现象，估计器的性能接近 DA 类算法的性能，明显优于直接判
决反馈时的性能。虽然该方法实现了低信噪比下信噪比的高精度估计，但计算比较复杂。文献 [5J 通过 M
538
信息工程大学学报
2011 年
次方去调制方法避开了估计中的判决过程，得到了一种低信噪比下性能也较好的估计器:
Ns-I
三 Re( r!)IN,
P = N.-l
三 rn 21N, - L Re(r!)IN,
, 0 运 NS -1 。
(1 2)
(1 2) 式各变量定义与(11)式相同。该估计器实现复杂度低，估计性能也较好，但是当 M 较大时，由 M
次方引人的噪声积累就越大，所以对估计性能的影响也就越大。研究和仿真表明，当 M = 4 时的性能基本
可以接受，但当 M 取更大值时，这种方法已经完全失效。文献 [5J 还从信道编码角度出发，提出了一种与前
向纠错编码结合的判决指向 SNR 估计方法。以上改进算法主要针对 BPSK 和 QPSK 信号，文献[ 1 J 利用 ML
类算法实现了对 M-APSK 信号的信噪比估计。文献 [9J 结合期望最大化 (EM) 和 ML 技术，研究了所有二维
线性调制信号的盲信噪比估计问题，并运用该方法成功地估计了 SIMO 系统下信号的信噪比，拓展了 ML
类方法的使用范围。
2.2 基于谱分析的估计方法
ML 类算法在取得良好性能的同时，其要求相对较高。因此，人们开始提出一些简单实用的信噪比估计
算法。文献 [10J 利用移动信道的功率谱特性，提出了一种基于谱分析的平均信噪比估计算法。对一般通信
系统的工作信噪比范围来说，该方法具有较高的估计精度。在基于谱分析的估计方法中，功率分布函数的
拐点是与信号频带有关的重要信息参数，通过检测该参数可精确估计信号的带宽和信噪比。文献 [11 J 提
出一种针对中频信号的无需先验信息的快速信噪比盲估计算法。其实现步骤如下:
①根据 Welch 平均周期图法计算观测信号的功率谱 X (f) ;
②对功率谱均值滤波，设计一定规则求信号所对应的频率范围 (λ - fH) ;
③对信号频率范围外的谱图进行直方图统计，得出噪声谱的均值 No ;
④将信号频率范围内的功率谱值减去噪声谱均值，得到信号的谱值;
⑤按下式计算观测信号信噪比:
pdB=10lg
X (f) df - No (儿 -λ)
NJ, 12
(1 3 )
其中，兀为接收信号的采样频率。该类算法可以方便地通过 FFT 来实现，能有效节省运算资源。同时，它不
需要任何先验信息即可完成对信号信噪比的估计，是一种鲁棒性非常强的算法，值得深入研究。文献
[ 12-13 J 比较了基于谱分析的信噪比估计方法与其它经典方法的性能。与经典方法相比，谱分析方法计算
量小，实现简单，能实时估计出信号信噪比。
2.3 基于统计量的估计方法
根据信号和噪声的统计特性的不同，通过构造统计量很容易区分信号和噪声。常用的基于统计量的信
噪比估计算法有:分隔符号矩( SSME: Split Symbol Moment Estimator) 、二阶四阶矩( M2M4) 、多项式拟合
以及子空间分解等。
2.3.1 SSME 算法
SSME 算法由美国喷气推进实验所首先提出，已用于美国国家航空和宇宙航行局的深层空间研究
中[ 14] 。该算法对匹配滤波器输入信号过采样后，将一个符号周期内的样点均匀地分为前后 2 段，分别计算
这 2 段接收数据的采样点之和，再利用同一符号周期内有用信号相关而噪声无关这一性质构造 2 个新的统
计量，最后用这 2 个统计量估计出信噪比的大小。
为便于分析，参照文献 [6 ]，将 (3) 式中的观测信号改为如下形式:
S
rik = 万"αk + n ik
(14 )
其中，向表示信号的真实星座点 ， k=1 ， 2 ， … ， N.. ， i=1 ， 2 ， … 1" ， NS 表示符号个数 ， N" 表示每符号采样点
数，那么 rik 表示第 k 个符号的第 i 个采样点。设每符号中信号能量为 S2 ，那么 S/N 表示每个采样点的信号
幅度。 nik 表示均值为零，方差为 NIN" 的复高斯白噪声样点。
第 5 期
张金成等:信噪比估计算法研究
539
为提高原算法估计精度，文献[ 15 J 提出了广义 SSME 算法( GSSME: Generalized SSME) 。原 SSME 算
法与 GSSME 算法对第 k 个符号进行分段方法见图 2 ，其中 M， = N，，ILk 。
从图 2 可以看出， GSSME 相当于将每个符号转化成 Lk 产-JL
个"短符号"进行处理，对每个"短符号"的信噪比估计均 ;
采用原 SSME 算法，得到 Lk 个信噪比估计值后，对其求算术
飞 f
i
Nu l2
( a) 原始SSME算法
Y"
J、
飞
』
N"
平均就得到了 GSSME 算法的估计结果。
研究表明，当信噪比高于一定值时， GSSME 算法更加
接近 CRLB 。这是因为信噪比较高时，尽管"短符号"中样点
较少，但已经可以确保原算法的估计结果落在真实值附近
点与江、
I M, /2 M,
」一!
I
A冉气.，.且具气
(l-I)M ,+I t IM,( L,-I)M,+I \
lVss
({-1/2)M,
( b)GSSME算法
(L,-I I2 )M,
一个较小的范围内，再通过对 L 次估值求平均则能够更好
地反映出真实信噪比的大小。文献 [16J 提出了计算最佳分段数 L 的自适应算法。但文献[ 15-16J 考虑的都
是实 AWGN 信道下 BPSK 信号的信噪比估计问题。文献 [6J 将 GSSME 算法推广到复 AWGN 信道中 MPSK
信号的信噪比估计，并利用信噪比估计值的标准差作为算法迭代是否终止的度量，有效解决了原 GSSME
图 2 原 SSME 算法与 GSSME 算法的分段方法
算法很难确定最佳选代次数的问题，同时还给出了确定最佳分段数 L 的方法。
总之， SSME 算法虽然实现了对 MPSK 信号信噪比的盲估计，但它要求发送端采取矩形成型的方式，否
则算法性能将会恶化。
2.3.2 M2M4 算法
早在 20 世纪 60 年代，就有人使用 M2M4 算法成功地对实 AWGN 信道中的载波强度和噪声强度进行估
计[川。文献 [7J 对 M2M4 算法的发展做了分析与总结，给出了实、复信道下基于 M2M4 算法的信噪比估计
器:
P2=O 5j6M~ - 2M4
M2M4"e81 M
_ O. 5斤两丁2M4
2
川4 叫
J2M;-M
(1 5 )
(1 6)
其中 M2 和 M4 表示接收信号的二阶矩和四节矩。在实际处理中，接收信号的统计平均是不可直接得到的，
通常的做法是采用时间平均替代统计平均。利用 (4) 式的观测信号，得到二阶、四阶矩的估计值为
M矶2 臼寸去 E |几川川|尸2
矶臼寸古 E| 川
(1 7)
M2M4 算法具有许多优点:首先，计算简单，只需要对观测信号做二次方、四次方处理即可得到信噪比
估值;其次，它是一种全盲的方法;第 3 ，对载波相位偏差不敏感。与其它基于统计量的算法一样， M2M4 算
法随着观测数据的增加，估计值越来越接近真实值，是一致估计器。研究发现，当估计符号个数在 20∞O∞O 以
上时，信噪比估计值的标准差不超过 0.2d扭B 。此外，该方法还能用于估计平坦衰落信道中信号的信噪
比[ 18 J 。
由于 M2M4 算法具有这些优点，能够满足一般常见场合下的信噪比估计要求，应用比较广泛。遗憾的
是，当信号调制阶数增加时，该方法随着信噪比的升高估计偏差越来越大。为充分利用 M2M4 算法的优点，
克服其不足，文献 [19J 研究了基于接收信号的高阶统计量的盲信噪比估计新方法，改善了 M2M4 算法在
高阶调制时和高信噪比条件下的性能。文献 [20J 则进一步研究了该类算法在 SIMO 系统中的性能。
2.3.3 多项式拟合法
多项式拟合法是一类十分重要的盲信噪比估计方法，经常与 Turbo 码 [24 ， 27J 及 LDPC 码[ 22] 等译码算
法结合使用，也可以用来估计衰落信道下[刀]观测信号的信噪比。这类方法主要通过寻求观测信号统计量
的比值与信噪比的关系实现对信噪比的盲估计。文献 [21J 给出了 AWGN 信道下 BPSK 信号信噪比与 2 统
计量之比的关系式:
540
信息工程大学学报
2011 年
f(p) = ,_ _
E [y! 1
, - n
,? =
t ' /
(E[ Yn 1])2
1 + 2p
[ l2ï石e-P+AJey:f(JF)]2
(1 8 )
其中 ， Yn 为观测信号，ρ 为信噪比 ， erfC .)为误差函数。令 g() =]1 () ，则信噪比估计值 :p = g (jCρ) )。其中
(1 8 )式计算比较复杂，很难直接得到反函数 gC .) ，通常做法是通过数据拟合的方式，在一定信噪比范围
内(即需要估计的信噪比范围)进行多项式近似，故该方法称为多项式拟合法。为了拓展该方法的应用范
围，文献 [5J 采取实、虚部分开的方式，推导了复 AWGN 信道下 QPSK 信号及 QAM 信号的盲信噪比估计
器，在感兴趣的范围内实现信噪比的盲估计。进一步研究发现，该算法还可以与 AWGN 信道下 Turbo 编码
系统中的定时同步算法结合，联合完成定时同步和译码 [25 J 。
文献 [7J 利用 2 个不同统计量之比，得到了比(1 8 )式简单的关系式:
f (p )== (19 )
EfynYJYn-IY;-1}ρ2 + 2p + 1
E{ C YnY: )2}_ E{yS: Yn-1Y:-1}
C ka - 1)/ + 2p + C kw + 1)
该算法还称为信号方差比( SVR) 方法。令 β = fCp) ， 易得信噪比估计值的表达式:
p-(β- 1)+ .j Cβ_ 1) 2-[1-β(kaE1)][1-βC kw - 1)]
SVR
-
1 _β(ka-1)
(20)
其中，对复 AWGN 信道下的 MPSK 信号来说:札= 1 和札 =2; 对实 AWGN 信道下的 BPSK 信号来说:札=
1 和 kw=3 。
2.3.4 子空间分解法
子空间类算法最早用于窄带 TDMA 蜂窝通信系统 [26-27J 的信噪比估计当中，它利用训练序列来构造接
收信号的自相关矩阵，然后再利用子空间 (SB) 分解算法得到信号与噪声功率的估计》从而计算出较为精
确的实时信噪比。子空间类算法的理论基础是:接收信号自相关矩阵进行特征值分解可以得到信号子空间
和噪声子空间，信号子空间对应的特征值之和为信号功率与噪声功率之和，噪声子空间则只对应噪声功
率。但该方法需要周期地发送训练序列以估计接收信号的信噪比，降低了系统的频带利用率。文献 [28J 提
出了不需要训练序列的盲信噪比估计算法，并研究了该算法在多径信道下的估计性能。
子空间分解算法主要有 3 个研究方向:一是如何构造接收信号的自相关矩阵，文献 [28J 给出了自相
关矩阵维数的经验值 50~100; 二是如何准确地估计出信号子空间维数;三是该方法涉及一个 50 维-100 维
的矩阵分解，如何降低计算复杂度是近年研究的重点。文献 [29J 利用紧缩投影近似子空间跟踪( PASTd)
代替子空间算法中的子空间分解，并将 Gram-Schmidt 正交化过程引入到 PASTd 中，以确保得到的特征向
量相互正交，使算法具有很好的收敛性，提出了一种新的基于改进 PASTd 的中频信号盲信噪比估计算法，
在性能基本不变的条件下，大大降低了算法的复杂度。以上算法在信噪比较低时( < 5 dB) ，均会因维数估
计错误导致信噪比估计性能下降。为提高低信噪比下估计性能，文献 [30J 利用信号的过采样率信息构造特
定维数( < 50) 的自相关矩阵，避免了对信号和噪声子空间维数的估计，提出了一种新的基于子空间分解的
盲信噪比估计算法，提高了估计的精度，并且计算复杂度也有所降低。同时，为了进一步降低算法的复杂度，
以及更好地跟踪信噪比的时变，文献 [30J 提出基于 PASTd 的子空间跟踪算法对时变信噪比进行跟踪估计。
3 性能分析与仿真比较
表 1 列出了现有各信噪比算法应用条件。为直观分析各算法性能，本小节就不同条件下对各算法进行
仿真比较。仿真中，采取下式的估计偏差和均方误差作为衡量算法性能的评价标准:
Bias(ρ)=tz(PU)-p)
MSE(p) = 走 Z(P( 川)2
N
(21)
其中 ， Nmc 为蒙特卡洛仿真次数，pC i) 为第 i 次仿真的估值 ，p 为信噪比真实值。表中‘ V' 表示算法在该条件
第 5 期
下有效。
张金成等:信噪比估计算法研究
541
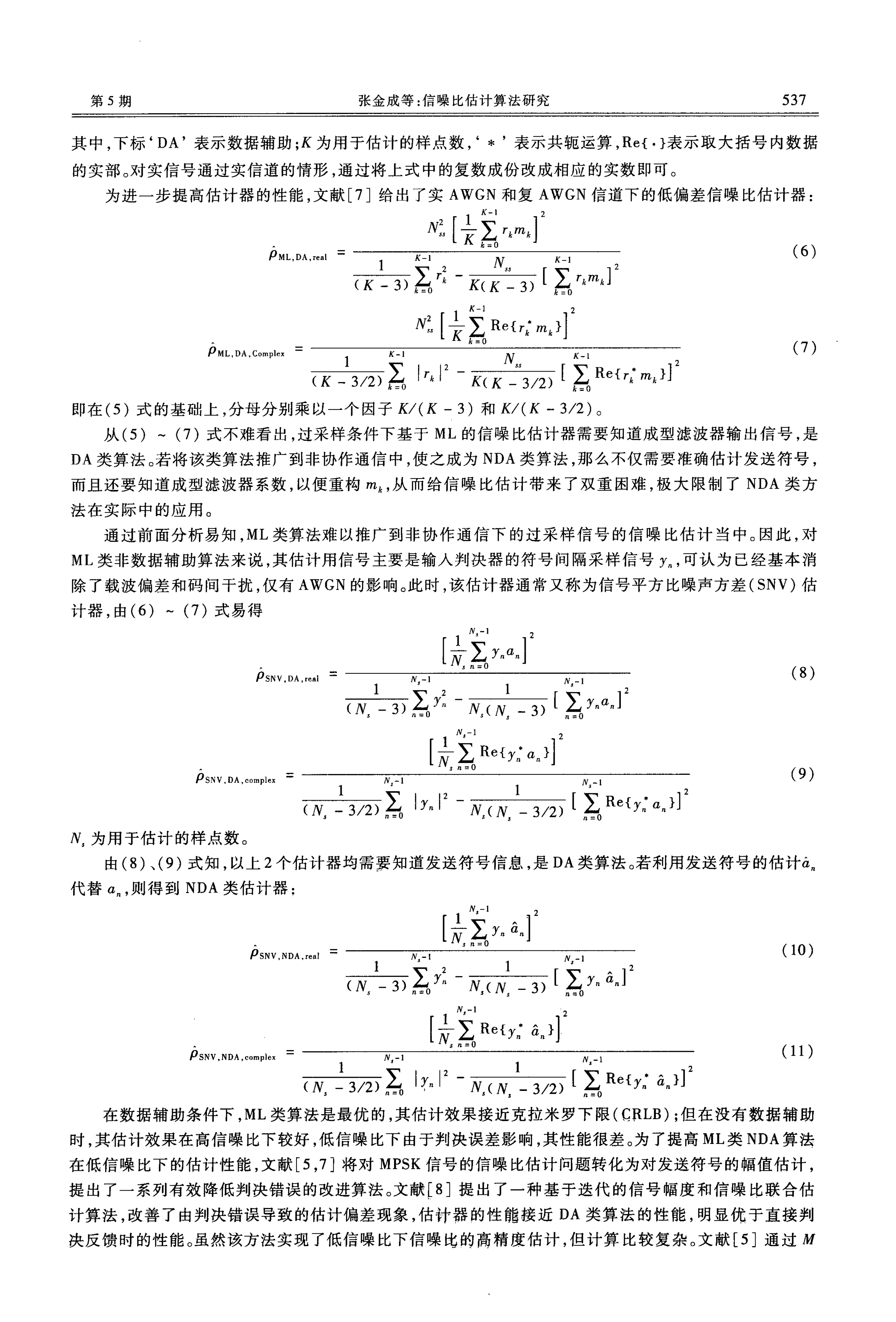
实验 1 矩形成型时，匹配滤波器输入信
号信噪比估计
SSME 算法主要用于估计实 AWGN 信道下
BPSK 信号的信噪比。本实验以 BPSK 信号为
例，仿真比较各算法性能。对于 BPSK 信号来
说，人们感兴趣的信噪比一般较低，因此这里信
噪比估计范围取为- lOdB -10dB 。图 3 和图 4
给出了各算法的估计偏差、均方误差与信噪比
表 1 备信噪比估计算法应用条件
条件
且Li 回己滤波器输入
一
矩形成型 升余弦成型
判决器输入
算法
ML 类
谱分析类
DA
NDA
>
>
>
>
>
>
>
>
>
>
SSME
M2M4
统计量类 多项式拟合
子空间法
的关系。其中‘ MLDA' 和‘ MLNDA' 分别表示基于 ML 的 DA 和 NDA 算法，‘ SUB1 '和‘ SUB2' 分别为文献
[28 J 和文献 [30J 中的方法。
10 '
10'
喇
喇
耐m
h
k交
、
、
10
~ MLDA
~ MLNDA
- e -SSME
-也-SUBI
-号 -SUB2
bt==@=-B" 毡，
、守--气，...
、、任 --Q
-0.5
115
-2
-2.5
-3
-3.5
& MLDA
-叶-MLNDA
-" -SSME
-击-SUBI
-号 -SUB2
-4
-10 -8 -6
-4
-2
0
2
4
6
8
10
10-2
10
-8 -6
一4
-2
0
2
4
6
8
10
信噪比 /dB
{言噪比 /dB
图 3 估计偏差与信噪比关系曲线
图 4 估计均方误差与信噪比关系曲线
从图 3 、4 可以看出， NDA 类 ML 算法在低信噪比时性能很差，这是因为此时符号容易发生误判，进而
使估计的信号功率比实际值要小，信噪比估值也比实际值要小。当信噪比大于某一定值(对 BPSK 来说约
为 8dB) 时，可认为判决无误，此时 NDA 算法获得了与 DA 算法相近的性能。子空间类算法在低信噪比下
性能不是很理想，这主要是低信噪比下易造成信号子空间维数的过估计，使得信噪比估计值较真实值大。
‘ SUB1 '算法由于自相关矩阵维数高，能更好地反映出现测信号的统计特性，性能较‘ SUB2' 稍好。与上述
3 种算法随信噪比下降时性能呈现恶化趋势不同， SSME 算法和 DA 类 ML 算法对信噪比的鲁棒性较好。
综合比较各算法性能和计算复杂度，对实 AWGN 信道下 BPSK 信号，当发送端使用矩形成型时，宜采
取 SSME 算法估计其信噪比。
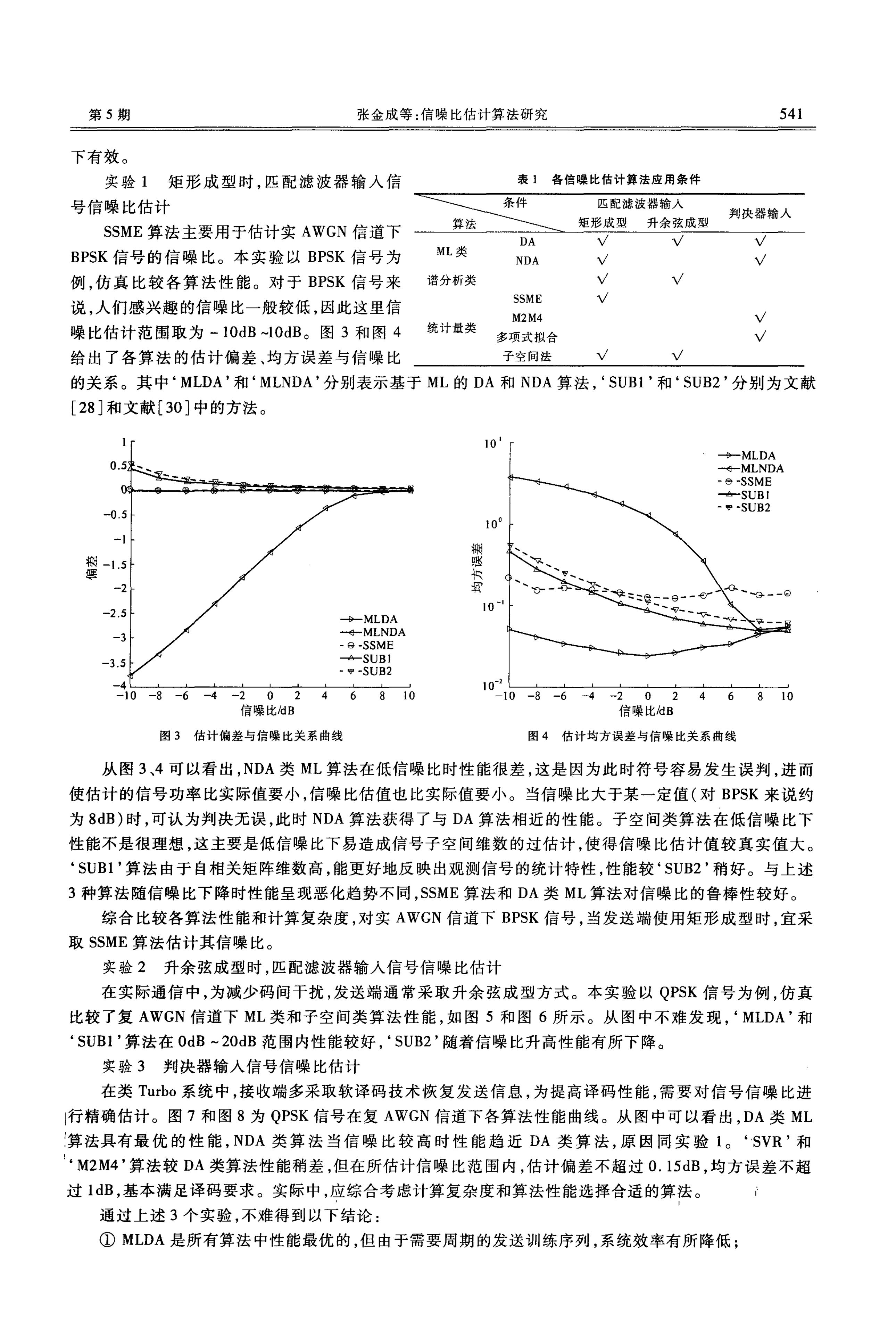
实验 2 升余弦成型时，匹配滤波器输入信号信噪比估计
在实际通信中，为减少码间干扰，发送端通常采取升余弦成型方式。本实验以 QPSK 信号为例，仿真
比较了复 AWGN 信道下 ML 类和子空间类算法性能，如图 5 和图 6 所示。从图中不难发现，‘ MLDA' 和
‘ SUBl' 算法在 OdB -20dB 范围内性能较好，‘ SUB2' 随着信噪比升高性能有所下降。
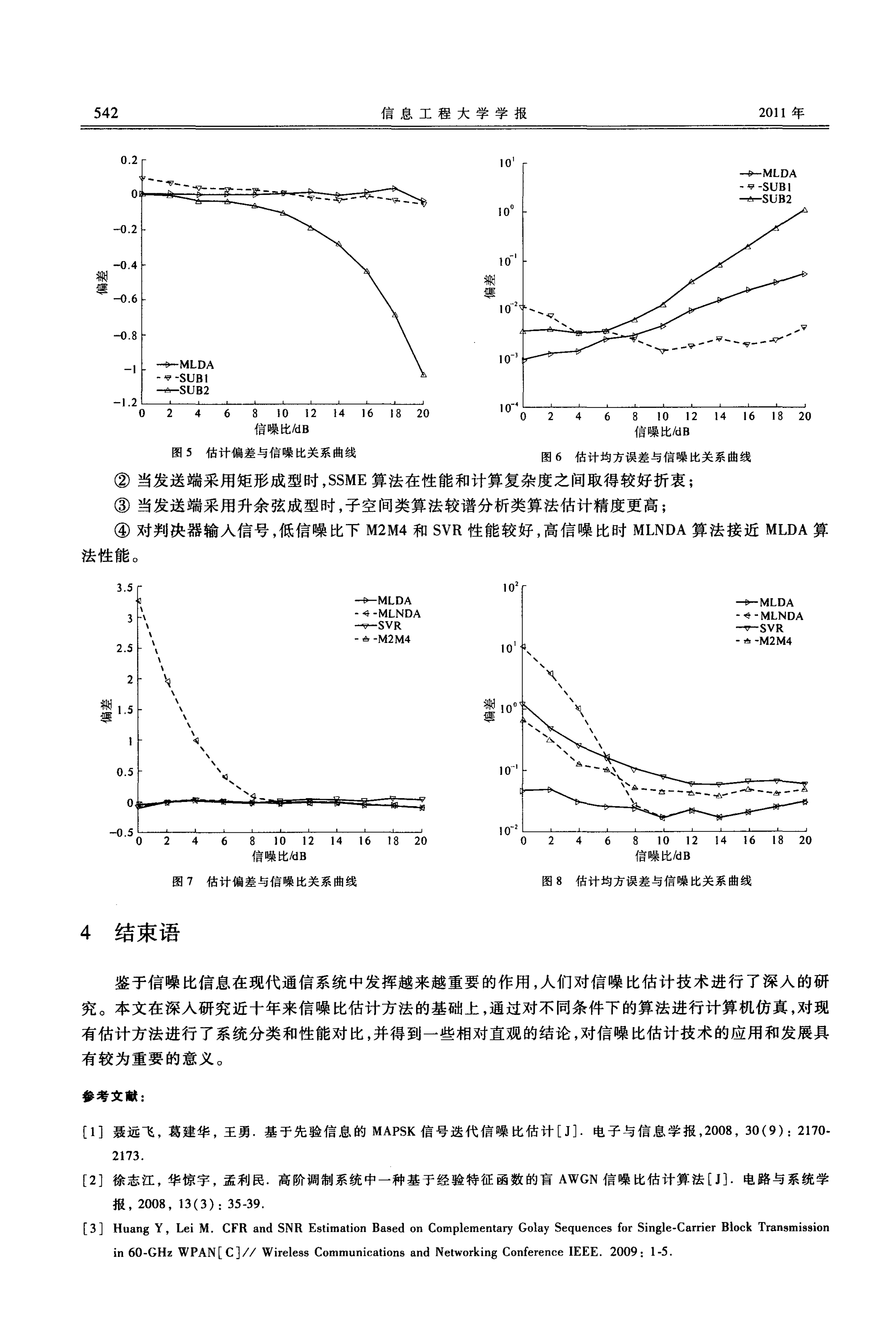
实验 3 判决器输入信号信噪比估计
在类 Turbo 系统中，接收端多采取软译码技术恢复发送信息，为提高译码性能，需要对信号信噪比进
l 行精确估计。图 7 和图 8 为 QPSK 信号在复 AWGN 信道下各算法性能曲线。从图中可以看出， DA 类 ML
!算法具有最优的性能， NDA 类算法当信噪比较高时性能趋近 DA 类算法，原因同实验 10 "SVR' 和
" M2M4' 算法较 DA 类算法性能稍差，但在所估计信噪比范围内，估计偏差不超过 O. 15dB ，均方误差不超
过 1dB ，基本满足译码要求。实际中，应综合考虑计算复杂度和算法性能选择合适的算法。
通过上述 3 个实验，不难得到以下结论:
① MLDA 是所有算法中性能最优的，但由于需要周期的发送训练序列，系统效率有所降低;
542
0.2
。
-0.2
-0 .4
:IlIlJ
4重-0.6
-0 .8
-1. 2
0
信息工程大学学报
2011 年
--专，-‘-~，- -
-
-MLDA
'甲 -SUBl
-告-SUB2
2
4
6
10
8
信噪比 /dB
12
14
16
18
20
图 5 估计偏差与信噪比关系曲线
1 0 '
100
10- 1
:IIl日
零
10-' 1-、、 q
、
、
10-3
& MLDA
·甲 -SUBl
-舍-SUB2
、、勺~--字'
帘__-'7"
，号-
v
,
,
{言噪比/dB
图 6 估计均方误差与信噪比关系曲线
②当发送端采用矩形成型时， SSME 算法在性能和计算复杂度之间取得较好折衷;
③当发送端采用升余弦成型时，子空间类算法较谱分析类算法估计精度更高;
④对判决器输入信号，低信噪比下 M2M4 和 SVR 性能较好，高信噪比时 MLNDA 算法接近 MLDA 算
法性能。
3.5
3
、
、
句
，
&
ζ
d
l
「
'
「
、
飞
、
、
饨
，
‘
事1.5
飞
。
飞
、
、
、
、
、
、‘
、
、
、
、
喝
、
、
0.5
。
-0 .5 o
2
4
6
~ MLDA
-4-MLNDA
-甲-SVR
，合 -M2M4
10'
nu
理 10 0
~ MLDA
- .令 -MLNDA
" SVR
-"'-M2M4
、
M
飞
、
、
、
、
、
、
气
、
飞
、
.
、
、
‘
、
、
、A
10
L
AZ
、
、
、
、
、
、
、
A
昌
、
B
咀-4E
,
-t;. --Æ墅--
14
16
18
20
10-'
o
2
4
6
10
8
f言噪比 /dB
12
14
16
18
20
10
8
f言噪比 /dB
12
图 7 估计偏差与信噪比关系曲线
图 8 估计均方误差与信噪比关系曲线
4 结束语
鉴于信噪比信息在现代通信系统中发挥越来越重要的作用，人们对信噪比估计技术进行了深入的研
究。本文在深入研究近十年来信噪比估计方法的基础上，通过对不同条件下的算法进行计算机仿真，对现
有估计方法进行了系统分类和性能对比，井得到一些相对直观的结论，对信噪比估计技术的应用和发展具
有较为重要的意义。
参考文献:
[ 1 ]聂远飞，葛建华，王勇.基于先验信息的 MAPSK 信号迭代信噪比估计[J] .电子与信息学报， 2008 ， 30 ( 9): 2170-
2173.
[2] 徐志江，华惊宇，孟利民.高阶调制系统中一种基于经验特征函数的盲 AWGN 信噪比估计算法[J] .电路与系统学
报， 2008 , 13 ( 3 ) : 35 -39.
[3 J Huang Y , Lei M. CFR and SNR Estimation Based on Complementary Golay Sequences for Single-Carrier Block Transmission
in 60-GHz WPAN [ C] 11 Wireless Communications and Networking Conference IEEE. 2009: 1-5.
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
