数学建模灾情巡视路线作业论文
灾情巡视路线模型
摘要
本文研究的是考察灾情最佳巡视线路设计的问题,属于多旅行商问题,为
此 我们建立了网络图模型。利用最小生成树图形和最短路树图形相结合,通过
分析、 计算比较得出最优解。
对于问题一:通过建立赋权网络图,同时利用 Matlab 编程
求解得到此网络图的最小生成树图和最短路径树图,而对于分组的问题,
经过参考相关论文,我们决定以两图相重合的部分为分批的依据,将需要视察
的地域分为三块。最后根据题意要求,设置目标函数为最短总路程和均衡度最
小为目标函数,将问题转化为多目标线性规划问题,最终用 Matlab 进行求解
(对于均衡度的解释详见模型的建立过程)。
对于问题二:在模型的建立过程中,我们发现三组无法满足问题二所提出
的要求,并且证明了最少有四组,才能满足题目所述条件,并用类似的方法求
出了对应的四组的最优路线设置。
�
对于问题三:在问题所述条件下,考虑到最短路径树,我们从树的末端
(也就是距离县政府最远的地点开始),逐渐向内巡视,同时保证所用时间不
大于所求出的最短时间,最终分为了 23 个组进行巡视,最短时间约为 6.43 小
时。
对于问题四:在不改变分组的前提下,对 T,t,V 的改变仅影响巡视时间,
在模型建立过程中我们找到了三者之间的关系并给出关系表
达式,从而根据所得关系得出结论。
关键词:最小生成树,均衡度,哈密顿算法
�
一、 问题重述
下图为某县的乡(镇)、村公路网示意图,公路边的数字为该路段的公
里数。今年夏天该县遭受水灾。为考察灾情、组织自救,县领导决定,带领
有关部门负责人到全县各乡(镇)、村巡视。巡视路线指从县政府所在地出
发,走遍各乡(镇)、村,又回到县政府所在地的路线。
1. 若分三组(路)巡视,试设计总路程最短且各组尽可能均衡的巡视路线。
2. 假定巡视人员在各乡(镇)停留时间 T=2 小时,在各村停留时间 t=1 小
时,汽车行驶速度 V=35 公里/小时。要在 24 小时内完成巡视,至少应分几
组;给出这种分组下你认为最佳的巡视路线。
3. 在上述关于 T,t 和 V 的假定下,如果巡视人员足够多,完成巡视的最短
时间是多少;给出在这种最短时间完成巡视的要求下,你认为最佳的巡视路
线。
4. 若巡视组数已定(比如三组),要求尽快完成巡视,讨论 T,t 和 V 改变
对最佳巡视路线的影响。
图 1.题目图
�
二、 模型假设
2.1 汽车在路上的速度总是一定,不会出现抛锚等现象;忽略天气、故障等
因素的影响。
2.2 巡视当中,在每个乡镇、村的停留时间一定,不会出现特殊情况而延误
时间。
2.3 每个小组的汽车行驶速度完全一样;
2.4 各巡视组行动统一,一个巡视组不可再分成若干小组。
2.5 情况不受灾情影响,即车辆在所有公路上所有公路上都可以顺利通过。
三、 变量以及符号说明
:第 i 个小组所走路程
:均衡度
:巡视一个乡镇所花时间
:巡视一个村所花时间
:汽车形式速度
:第 i 个小组巡视所用时间
:最短路径树中从县政府到所有点中最远距离。
:最短路径树中点 j 距出发点的距离
:完成所有巡视所用的最短时间
:巡视完所规定的点剩余的时间
:小组巡视乡镇的个数
:小组巡视村的个数
四、 问题分析
本问题属于旅行商问题的拓展,相当于在有多位旅行商的基础上进行问题
的设置,多条路线,且起点相同,最终带权路径长度总和最小,而回到题目中,
第一题则是由三位“旅行商”,第二题则是有四位“旅行商”。
本题给出了某县的公路网络图,要求的是在不同的条件下,灾情巡视的最
分组方案和路线.将每个乡(镇)或村看作一个图的顶点,各乡镇、村之间的公
路看作此图对应顶点间的边,各条公路的长度(或行驶时间)看作对应边上的
权,所给公路网就转化为加权网络图,问题就转化图论中一类称之为旅行售货
员问题,即在给定的加权网络图中寻找从给定点 O 出发,行遍所有顶点至少一
�
次再回到点 O,使得总权(路程或时间)最小。
对于问题一,题目要求在分三组巡视的情况下,使总路程最短且各小组所
走路程均衡。先考虑分区,我们将得出的最小生成树图形和最短路树图形,进
行比较并找出其公共部分。分组要求尽量不破坏最短生成树和最小生成树,所
以我们 以公共部分为界限,将此网络图分为三组。为使每小组所走路程均衡,
我们引入了均衡度。它表示最大路程和最小路程的差值与最大路程的比值。α
越小,表示均衡度越好。以总路程最短和均衡度最小作为目标函数建立多目标
规划模型,利用哈密顿原理得出各组的巡回路线,并对其分析修正求得各组最
优巡回路线。
对于问题二,要求 24 小时内完成所有巡视。通过第一问的结果,求得在
分三组的情况下所用的平均时间1=13(17+35+609.835 )=28.8h 大于 24 小时,
所以我们先考虑分四组。我们的分组原则为:1、每子区域所分得的点近似相等;
2、尽量使每一个子区域连通;3、使每一个子区域中与点 O 的最短路上的点在
该区域内。根据以上分组原则将整个图大致划分为四个子图,同样利用哈密顿
算法求得在相对均衡的情况每个小组的最短路径和所需时间。如果部分时间大
于 24 小时,则调整分组方式;若所有时间均大于 24 小时再考虑多加一组。直
到找到相对均衡条件下的最佳路线。
对于问题三,考虑在人员足够多的情况下,求出最短的巡视时间。假设一
个 小组只巡视一个点的情况下,则去巡视离 O 点最远的点所花时间最长。我们
以巡 视小组中所耗时间最长的小组所用时间作为这次整个巡视的最短时间。要
使这次巡视时间最短,则要求去巡视离县镇府最远的点所花时间最小。当此小
组只巡视 H 时,最小。在不超过的情况下,根据其他小组的剩余时间
确定沿途是否巡视其他点。其中巡视原则为:①当一组人员巡视完规定点后时,
在剩余时间允许的情况下,优先考虑原巡视点附近而距离 O 较远的点,②最大
限度使用剩余时间,主要考虑原则①。按照此原则,逐个巡视,直至巡视完所
有点。
对于问题四,若巡视组数已定,则每个小组的最短路径就已确定,T、t、V
改变只影响的是整个的巡视时间。要求尽快完成巡视,即巡视时间要尽可能小。
巡视时间包括到巡视点的行驶时间和在巡视点的停留时间。行驶时间主要取决
于速度 V,而停留时间由 T、t 决定。所以此问题讨论的是当 T、t、V 改变时对
�
巡视时间的影响,即对 T、t、V 的灵敏度分析。
五、 模型的建立与求解
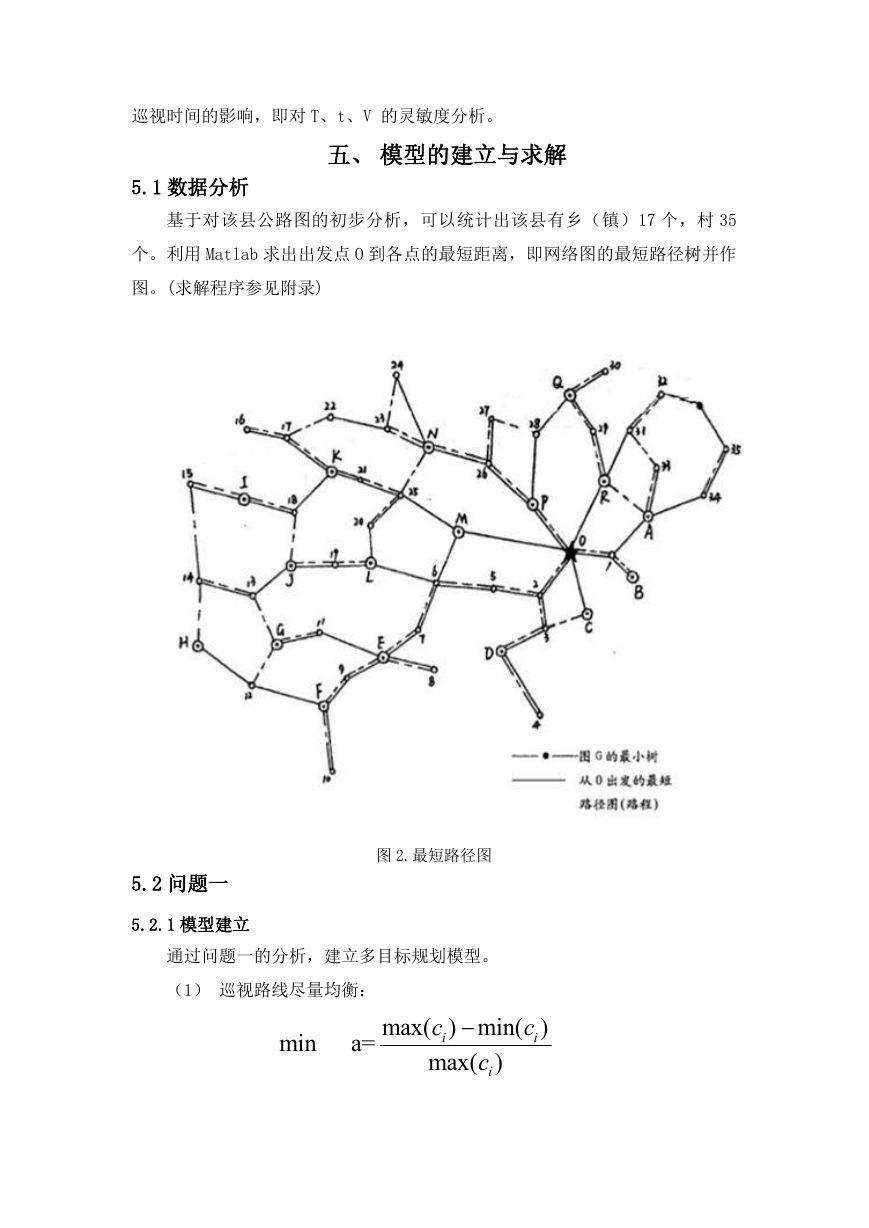
5.1 数据分析
基于对该县公路图的初步分析,可以统计出该县有乡(镇)17 个,村 35
个。利用 Matlab 求出出发点 O 到各点的最短距离,即网络图的最短路径树并作
图。(求解程序参见附录)
图 2.最短路径图
5.2 问题一
5.2.1 模型建立
通过问题一的分析,建立多目标规划模型。
(1) 巡视路线尽量均衡:
min
a=
max(
) min(
c
i
max(
)
c
i
c
i
)
�
(2) 三组巡视的总路线最短:
min
3
i
1
c
i
设当 a < 15 .0 时,认为均衡度比较好。 综上得出目标函数:
min
min
c
i
3
1
i
a
st. 每个小组走的路必须是回路
同时有决策变量为:,= 1,乡镇村,间有巡查团通过
0,乡镇村,间无巡查团通过
① =1 =1,=1,2,3,…,
�② =1 =1
,=1,2,3,…,
�
③−+≤−1,≠,,=2,3,…,
④=0 或1
⑤≥0,=1,2,..,
⑥=35
可得约束条件为:
约束式 ①保证只能到达每个城市一次,约束式②保证只能离开一个城市一
次,约束式③确保:1.由解得到的任何圈一定包含城市 1(即县镇府点 O);2.
包含全部城市的圈是可行的。
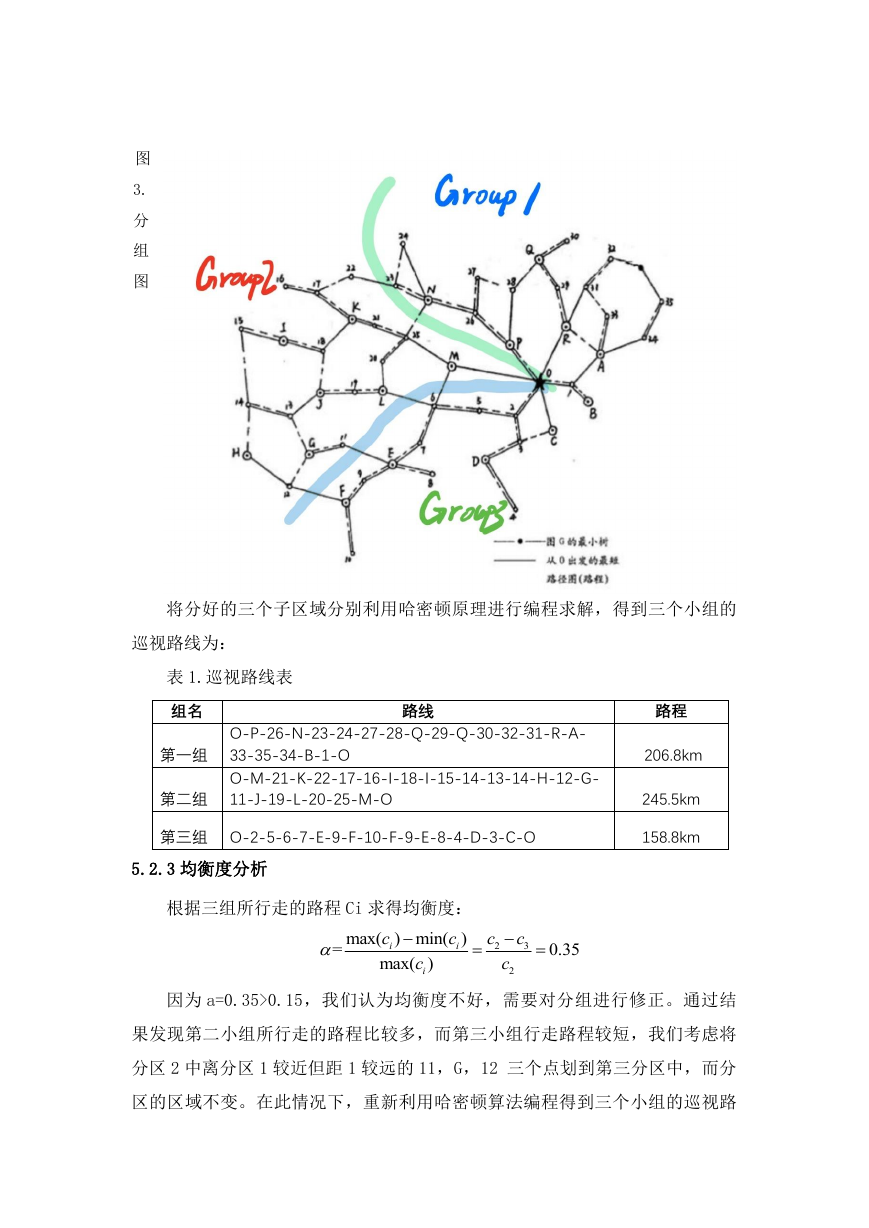
5.2.2 模型求解
根据问题一的分析,根据两图的公共部分作为分组的界限,分组图如下:
�
图
3.
分
组
图
将分好的三个子区域分别利用哈密顿原理进行编程求解,得到三个小组的
巡视路线为:
表 1.巡视路线表
组名
第一组
第二组
路线
O-P-26-N-23-24-27-28-Q-29-Q-30-32-31-R-A-
33-35-34-B-1-O
O-M-21-K-22-17-16-I-18-I-15-14-13-14-H-12-G-
11-J-19-L-20-25-M-O
第三组 O-2-5-6-7-E-9-F-10-F-9-E-8-4-D-3-C-O
路程
206.8km
245.5km
158.8km
5.2.3 均衡度分析
根据三组所行走的路程 Ci 求得均衡度:
)
max(
c
i
=
) min(
c
i
max(
)
c
i
c
3
c
2
c
2
0.35
因为 a=0.35>0.15,我们认为均衡度不好,需要对分组进行修正。通过结
果发现第二小组所行走的路程比较多,而第三小组行走路程较短,我们考虑将
分区 2 中离分区 1 较近但距 1 较远的 11,G,12 三个点划到第三分区中,而分
区的区域不变。在此情况下,重新利用哈密顿算法编程得到三个小组的巡视路
�














 2023年江西萍乡中考道德与法治真题及答案.doc
2023年江西萍乡中考道德与法治真题及答案.doc 2012年重庆南川中考生物真题及答案.doc
2012年重庆南川中考生物真题及答案.doc 2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc 2020年四川甘孜小升初语文真题及答案I卷.doc
2020年四川甘孜小升初语文真题及答案I卷.doc 2020年注册岩土工程师专业基础考试真题及答案.doc
2020年注册岩土工程师专业基础考试真题及答案.doc 2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc 2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc 2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc 2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc 2012年河北国家公务员申论考试真题及答案-省级.doc
2012年河北国家公务员申论考试真题及答案-省级.doc 2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc 2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc