第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
2022－2023学年广东深圳龙岗区七年级上册期末数学试卷及答案.doc
2022－2023 学年广东深圳龙岗区七年级上册期末数学试卷
及答案
一、选择题：（每道题只有一个正确选项，请将答题卡上的正确选项涂黑，每小题 3 分，共
30 分）
1. 龙岗某校七年级（1）班期末考试数学的平均成绩是 73 分，小亮得了 90 分，记作 17 分，
若小英的成绩记作 3 分，表示小英得了（）分．
A. 76
【答案】D
B. 73
C. 77
D. 70
2. 2022 年 11 月 5 日，第 23 届深圳读书月正式启动，本次读书月以“读时代新篇，创文明
典范”为主题，按照文明的阶梯、文化的闹钟、城市的雅集、阅读的节日四大板块，设置了
科学、人文、艺术三大专场，深圳读书月自创办以来，累计吸引 2.4 亿人次参与，将数据 2.4
亿（240000000）用科学记数法表示为（）
A.
9
0.24 10
B.
2.4 10
9
C.
8
2.4 10
D.
8
24 10
【答案】C
3. 下列是正方体展开图的是（ ）
A.
C.
【答案】B
B.
D.
4. 若单项式 3 2
ma
b 与
A.
6
【答案】B
1
2
nab 是同类项，则 mn 的值是（）
B.
4
C. 9
D. 4
5. 如果 1x 是关于 x 的方程3
x
m
2
的解，则 m 的值为（）
9
B. 1
C. 3
D. 6
B.
2
5
x
2
3
x
2
C.
2
x
x
3
x
D.
A.
1
3
【答案】C
6. 下列计算正确的是（）
A. 2
x
3
y
5
xy
8
y
3
y
5
y
【答案】D
7. 如图，点 O 在直线 AB 上，射线OD 是 AOC 的平分线，若
COB
40
，则 DOC
的度数是（）
A. 20°
【答案】D
B. 45°
C. 60°
D. 70°
8. 有理数 a，b 在数轴上对应的位置如图所示，则（
）
A. |
a
|
|
b
|
C.
a b
0
【答案】C
B.
ab
0
D.
a b
0
9. “鸡兔同笼”问题是中国古代著名典型趣题之一，大约在 1500 年前，《孙子算经》中就
记载了这个有趣的问题：今有雄（鸡）兔同笼，上有三十五头，下有九十四足，问雉兔各几
何？这四句话的意思是：有若干只鸡兔同在一个笼子里，从上面数，有 35 个头，从下面数，
有 94 只脚．问笼中各有多少只鸡和兔？如果我们设有 x 只鸡，则可列方程（）
A. 2
x
4(35
x
) 94
C. 2
x
4(94
x
) 35
【答案】A
B. 4
x
2(35
x
) 94
D. 4
x
2(94
x
) 35
10. 如图所示，动点 P 从第一个数 0 的位置出发，每次跳动一个单位长度，第一次跳动一个
单位长度到达数1的位置，第二次跳动一个单位长度到达数 2 的位置，第三次跳动一个单位
长度到达数3 的位置，…，依此规律跳动下去，点 P 从 0 跳动 6 次到达 1P 的位置，点点 P 从
0 跳动 21 次到达 2P 的位置，…，点 1
P P P
P、、
3
n
2
在一条直线上，则点 P 从 0 跳动（）次
可到达 12P 的位置．
A. 595
【答案】B
B. 666
C. 630
D. 703
二、填空题：（本大题共 5 小题，每题 3 分，共 15 分）
第Ⅱ卷（非选择题）
11. 单项式
21
a b
5
的系数为__________．
【答案】
## 0.2
1
5
12. 如图所示的网格式正方形网格，∠ABC________∠DEF（填“>”，“=”或“<”）
【答案】＞
13. 如图，已知线段
AB
12cm
，点 C 在线段 AB 上，
AC
2
BC
，则 BC __________cm ．
【答案】4
14. 2022 年 11 月 13 日，全球首个“国际红树林中心”落地深圳，为了解学生对红树林生
态系统的认知水平，龙岗区某校对初中部 1200 名学生进行了红树林生态系统知识测试，并
从中抽取了 100 名学生的成绩进行统计分析，下列说法正确的是__________．（填序号）
①1200 名学生是总体；②100 名学生的测试成绩是总体的一个样本；
③样本容量是 100 名学生；④该校初中部每个学生的测试成绩是个体．
【答案】④
15. 龙岗某校积极响应“双减”政策，开展课后延时服务，七年级某数学兴趣小组在课后综
合实践活动中，把一个直角三角尺 AOB 的直角顶点 O 放在互相垂直的两条直线 PQ MN、
的垂足 O 处，并使两条直角边落在直线 PQ MN、 上，若将 AOB
绕着点 O 顺时针旋转一个
小于180 的角得到 A OB
则 POC
__________．
△
，射线OC 是 B OM
的角平分线且满足
A OC
2
A OM
，
【答案】60 或36
三、解答题（共 7 题，55 分）
16. 计算：
（1）
2
( 1)
1
2
| 2 |
（2）
2
1 1
13 3 6
78
7
2
【答案】（1）
（2） 27
【小问 1 详解】
解：原式
11
2
2
．
7
2
【小问 2 详解】
解：原式
2
1 1
13 3 6
1
1
2
13
6
3
12 26 13
78
78
78
78
27 ．
17. （1）化简：
2
3b
2
a
2
b
2
；
b
（2）先化简再求值：
2
2
a b
1
4
2
ab
1
2
2
b
2
2
a b
2
3
ab
，其中 1,
b
a
．
2
【答案】（1） 2
b
2
a ，（2）
5
2
2
ab
2
， 14
b
【分析】（1）先去括号，再按照整式的加减混合运算计算即可；
（2）先去括号，再按照整式的加减混合运算化简，最后将 a 和 b 的值带入求解即可．
【详解】解：（1）原式
2
3b
2
a
2
b
2
b
1
2
ab
2
a b
1
2
2
ab
2
b
2
2
a b
2
3
ab
2
2
3
ab
2
b
2
b
2
．
a
（2）原式
2
2
2
a b
2
b
，
2
2
a b
5
2
当 1,
b
ab
a
2
2
时，
5 1
2
10 4
2
原式
2
2
2
．
14
18. 解方程：
（1）8
y
3(3
y
2)
6
（2）
x
1 2
3
3
x
5
4 3
【答案】（1）
y
12
（2） 2
x
【分析】（1）去括号，合并同类项，移项，系数化为1，即可求解；
（2）去分母，移项，合并同类项，系数化为1，即可求解．
【小问 1 详解】
解：8
y
3(3
y
2)
6
8
y
9
y
6 6
y
12
y ，
12
∴原方程的解为
y ．
12
【小问 2 详解】
解：
x
1 2
3
3
x
5
4 3
x
1 2
3
15
4
3
x
5
3
15
5 (1 2 ) 3 (3
x
x
4) 45
12 45
12 45 5
5 10
10
x
19
x
x
9
x
9
x
38
x ，
2
∴原方程的解是 2
19. 如图，已知线 a 、b ，求作一条线段 c ，使 2c
x ．
a b
．
要求：不写画法，保留必要的作图痕迹．
【答案】作图见详解
【分析】画射线 AM ，用尺规在射线 AM 上取 AB a= ，取 BC a ，再以 C 点为起点，向
反方向取CD b ，则 AD 即为所求线段 c ．
【详解】解：如图如下，
AB a= ， BC a ，以 C 点为起点，向反方向，即CB 方向取CD b ，
∴
AD c
2
a b
．
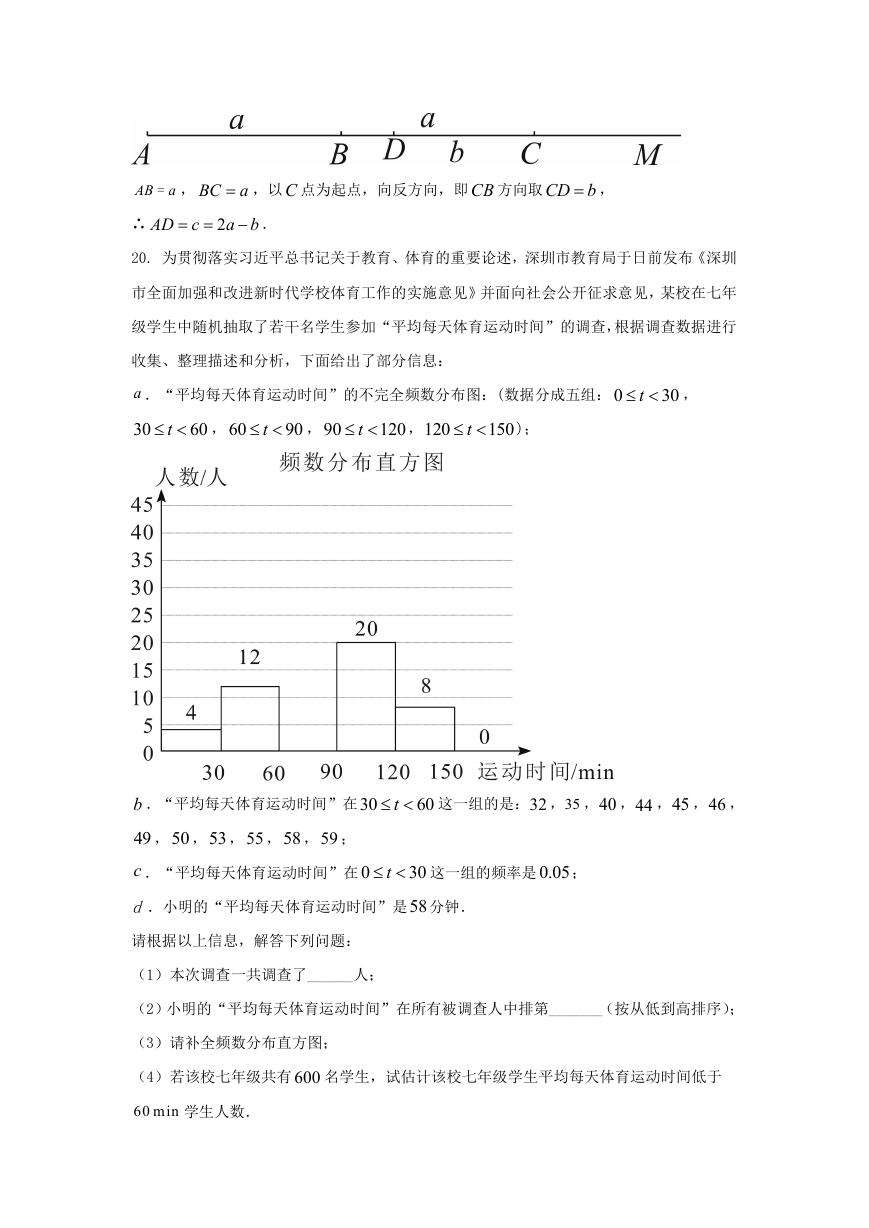
20. 为贯彻落实习近平总书记关于教育、体育的重要论述，深圳市教育局于日前发布《深圳
市全面加强和改进新时代学校体育工作的实施意见》并面向社会公开征求意见，某校在七年
级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查，根据调查数据进行
收集、整理描述和分析，下面给出了部分信息：
a ．“平均每天体育运动时间”的不完全频数分布图：(数据分成五组： 0
30
t ，120
t ，90
t ， 60
60
t
120
90
150
)；
t ，
30
t 这一组的是：32 ，35 ，40 ，44 ，45 ，46 ，
60
b ．“平均每天体育运动时间”在30
49 ，50 ，53 ，55 ，58 ，59 ；
c ．“平均每天体育运动时间”在 0
d ．小明的“平均每天体育运动时间”是58 分钟．
30
t 这一组的频率是 0.05 ；
请根据以上信息，解答下列问题：
（1）本次调查一共调查了______人；
（2）小明的“平均每天体育运动时间”在所有被调查人中排第_______（按从低到高排序）；
（3）请补全频数分布直方图；
（4）若该校七年级共有 600 名学生，试估计该校七年级学生平均每天体育运动时间低于
60 min 学生人数．
【答案】（1）80
（2）15
（3） 60
（4）120 人
【分析】（1）根据“平均每天体育运动时间”在 0
90
t 的人数为36 人，补全频数分布直方图见详解
t 这一组的频率是0.05 ，即可求出
30
本次调查一共调查的人数；
t 的有 4 人，30
30
t 的有12 人，小明是58 分钟，即可求解；
60
（2） 0
（ 3 ） 60
120
90
t ， 30
t 的人数，求出人数后即可补全频数分布直方图；
t 的 人 数 是 总 人 数 分 别 减 去 0
150
30
t ， 90
60
t
120
，
（4）运动时间低于 60 min 的频数为
4 12
80
，用 600 人乘以这个频率即可求解．
【小问 1 详解】
（人），即本次一共调查了80 人，
解： 4 0.05 80
故答案为：80 ．
【小问 2 详解】
30
30
60
t 的有 4 人，30
t 的有12 人，小明的时间是58 分钟，则从低到高的排
t 的有 4 人，32 ，35 ，40 ，44 ，45 ，46 ，49 ，50 ，53 ，55 ，58（小
解： 0
序是：0
明），59 ，
∴小明的“平均每天体育运动时间”在所有被调查人中排第名为：4 11 15
，即第15 名．
【小问 3 详解】
t 的人数为：80 4 12 20 8 36
（人），补全频数分布直方图，如图所
90
解：60
示，
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
