2020年湖南省邵阳市中考数学真题及答案.doc-资料库

第1页 / 共20页

第2页 / 共20页

第3页 / 共20页

第4页 / 共20页

第5页 / 共20页

第6页 / 共20页

第7页 / 共20页

第8页 / 共20页

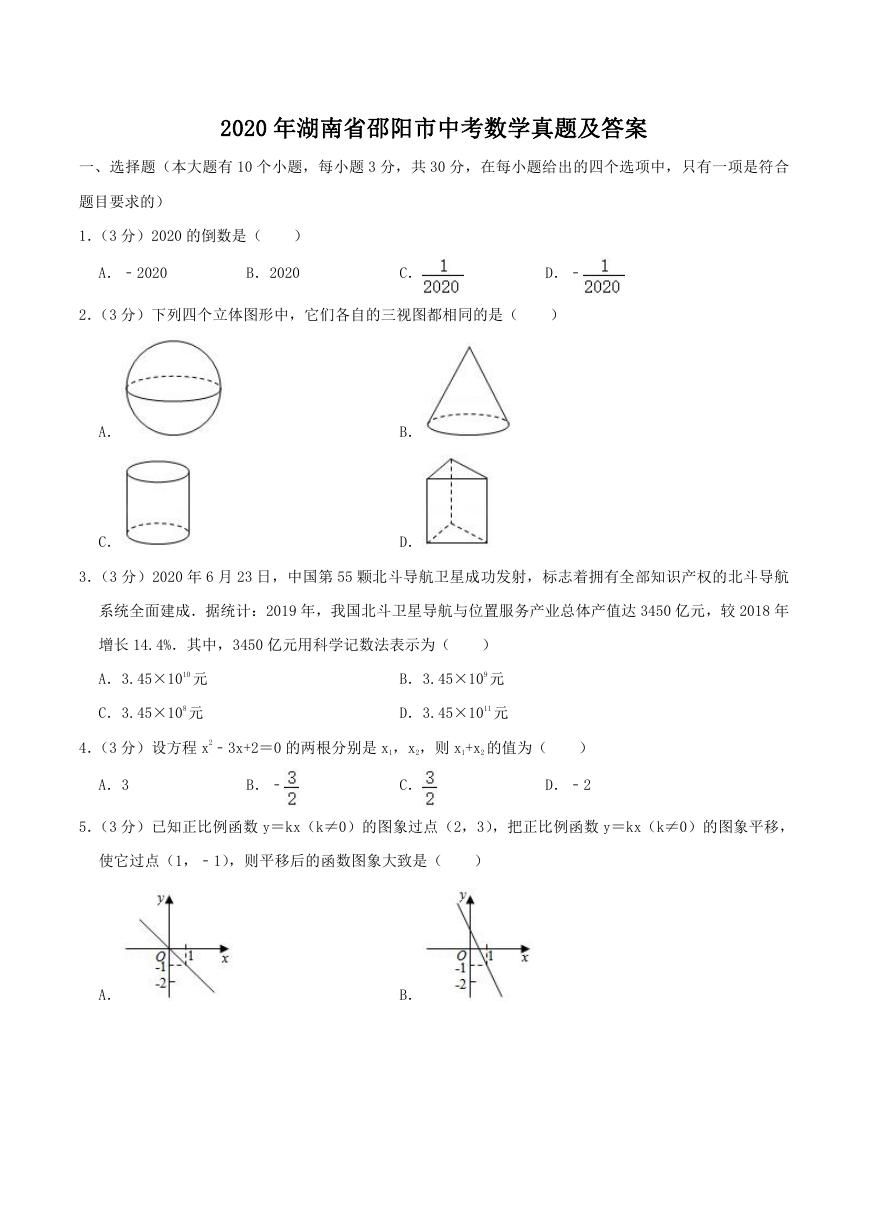
2020 年湖南省邵阳市中考数学真题及答案一、选择题（本大题有 10 个小题，每小题 3 分，共 30 分，在每小题给出的四个选项中，只有一项是符合题目要求的） 1．（3 分）2020 的倒数是（） A．﹣2020 B．2020 C． D．﹣ 2．（3 分）下列四个立体图形中，它们各自的三视图都相同的是（） A． C． B． D． 3．（3 分）2020 年 6 月 23 日，中国第 55 颗北斗导航卫星成功发射，标志着拥有全部知识产权的北斗导航系统全面建成．据统计：2019 年，我国北斗卫星导航与位置服务产业总体产值达 3450 亿元，较 2018 年增长 14.4%．其中，3450 亿元用科学记数法表示为（） A．3.45×1010 元 C．3.45×108 元 B．3.45×109 元 D．3.45×1011 元 4．（3 分）设方程 x2﹣3x+2＝0 的两根分别是 x1，x2，则 x1+x2 的值为（） A．3 B．﹣ C． D．﹣2 5．（3 分）已知正比例函数 y＝kx（k≠0）的图象过点（2，3），把正比例函数 y＝kx（k≠0）的图象平移，使它过点（1，﹣1），则平移后的函数图象大致是（） A． B．

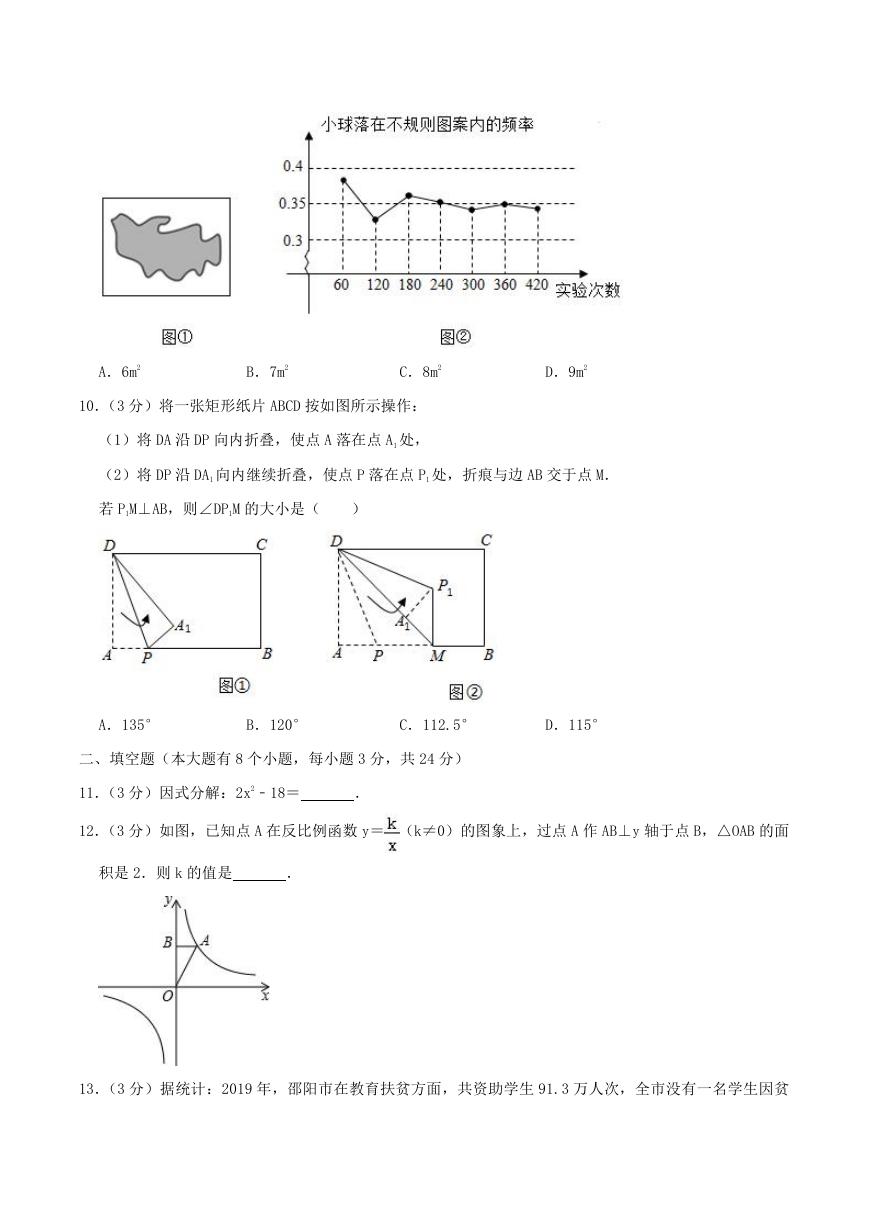
C． D． 6．（3 分）下列计算正确的是（） A．5 + ＝8 B．（﹣2a2b）3＝﹣6a2b3 C．（a﹣b）2＝a2﹣b2 D．＝a﹣2 7．（3 分）如图，四边形 ABCD 是平行四边形，点 E，B，D，F 在同一条直线上，请添加一个条件使得△ABE ≌△CDF，下列不正确的是（） A．AE＝CF B．∠AEB＝∠CFD C．∠EAB＝∠FCD D．BE＝DF 8．（3 分）已知 a+b＞0，ab＞0，则在如图所示的平面直角坐标系中，小手盖住的点的坐标可能是（） A．（a，b） B．（﹣a，b） C．（﹣a，﹣b） D．（a，﹣b） 9．（3 分）如图①所示，平整的地面上有一个不规则图案（图中阴影部分），小明想了解该图案的面积是多少，他采取了以下办法：用一个长为 5m，宽为 4m 的长方形，将不规则图案围起来，然后在适当位置随机地朝长方形区域扔小球，并记录小球落在不规则图案上的次数（球扔在界线上或长方形区域外不计试验结果），他将若干次有效试验的结果绘制成了②所示的折线统计图，由此他估计不规则图案的面积大约为（）

A．6m2 B．7m2 C．8m2 D．9m2 10．（3 分）将一张矩形纸片 ABCD 按如图所示操作：（1）将 DA 沿 DP 向内折叠，使点 A 落在点 A1 处，（2）将 DP 沿 DA1 向内继续折叠，使点 P 落在点 P1 处，折痕与边 AB 交于点 M．若 P1M⊥AB，则∠DP1M 的大小是（） A．135° B．120° C．112.5° D．115° 二、填空题（本大题有 8 个小题，每小题 3 分，共 24 分） 11．（3 分）因式分解：2x2﹣18＝． 12．（3 分）如图，已知点 A 在反比例函数 y＝（k≠0）的图象上，过点 A 作 AB⊥y 轴于点 B，△OAB 的面积是 2．则 k 的值是． 13．（3 分）据统计：2019 年，邵阳市在教育扶贫方面，共资助学生 91.3 万人次，全市没有一名学生因贫

失学，其中，某校老师承担了对甲，乙两名学生每周“送教上门”的任务，以下是甲、乙两名学生某十周每周接受“送教上门”的时间（单位：小时）：甲：7，8，8，9，7，8，8，9，7，9；乙：6，8，7，7，8，9，10，7，9，9．从接受“送教上门”的时间波动大小来看，学生每周接受送教的时间更稳定．（填“甲”或“乙”） 14．（3 分）如图，线段 AB＝10cm，用尺规作图法按如下步骤作图．（1）过点 B 作 AB 的垂线，并在垂线上取 BC＝ AB；（2）连接 AC，以点 C 为圆心，CB 为半径画弧，交 AC 于点 E；（3）以点 A 为圆心，AE 为半径画弧，交 AB 于点 D．即点 D 为线段 AB 的黄金分割点．则线段 AD 的长度约为 cm．（结果保留两位小数，参考数据：＝1.414，＝1.732，＝2.236） 15．（3 分）在如图方格中，若要使横、竖、斜对角的 3 个实数相乘都得到同样的结果，则 2 个空格的实数之积为． 3 1 2 3 6 16．（3 分）中国古代数学家杨辉的《田亩比数乘除减法》中记载：“直田积八百六十四步，只云阔不及长一十二步，问阔及长各几步？翻译成数学问题是：一块矩形田地的面积为 864 平方步，它的宽比长少 12 步，问它的长与宽各多少步？利用方程思想，设宽为 x 步，则依题意列方程为． 17．（3 分）如图①是山东舰航徽的构图，采用航母 45 度破浪而出的角度，展现山东舰作为中国首艘国产舰母橫空出世的气势，将舰徽中第一条波浪抽象成几何图形，则是一条长为 10π的弧，若该弧所在的扇形是高为 12 的圆锥侧面展开图（如图②），则该圆锥的母线长 AB 为．

18．（3 分）如图，在 Rt△ABC 中，∠ACB＝90°，斜边 AB＝，过点 C 作 CF∥AB，以 AB 为边作菱形 ABEF，若∠F＝30°，则 Rt△ABC 的面积为．三、解答题（本大题有 8 个小题，第 19～25 题每题 8 分，第 26 是 10 分，共 66 分．解答应写出必要的文字说明，演算步骤或证明过程） 19．（8 分）计算：（﹣1）2020+（）﹣1+|﹣1+ |﹣2sin60°． 20．（8 分）已知：|m﹣1|+ ＝0，（1）求 m，n 的值；（2）先化简，再求值：m（m﹣3n）+（m+2n）2﹣4n2． 21．（8 分）如图，在等腰△ABC 中，AB＝AC，点 D 是 BC 上一点，以 BD 为直径的⊙O 过点 A，连接 AD，∠CAD ＝∠C．（1）求证：AC 是⊙O 的切线；（2）若 AC＝4，求⊙O 的半径． 22．（8 分）2019 年 12 月 23 日，湖南省政府批准，全国“十三五”规划重大水利工程﹣﹣邵阳资水犬木塘水库，将于 2020 年开工建设施工测绘中，饮水干渠需经过一座险峻的石山，如图所示，AB，BC 表示需铺设的干渠引水管道，经测量，A，B，C 所处位置的海拔 AA1，BB1，CC1 分别为 62m，100m，200m．若管

道 AB 与水平线 AA2 的夹角为 30°，管道 BC 与水平线 BB2 夹角为 45°，求管道 AB 和 BC 的总长度（结果保留根号）． 23．（8 分）“新冠病毒”疫情防控期间，我市积极开展“停课不停学”网络教学活动，为了了解和指导学生有效进行网络学习，某校对学生每天在家网络学习时间进行了随机问卷调查（问卷调查表如图所示），并用调查结果绘制了图①，图②两幅统计图（均不完整），请根据统计图解答以下问题： xx 学校“停课不停学”网络学习时间调查表亲爱的同学，你好！为了了解和更好地指导你进行“停课不停学”网络学习，请在表格中选择一项符合你学习时间的选项，在其后的空格内打“√”．平均每天利用网络学习时间问卷调查表选项学习时间（小时） A B C D 0＜t≤1 1＜t≤3 3＜t≤5 t＞5

（1）本次接受问卷调查的学生共有人；（2）请补全图①中的条形统计图；（3）图②中，D 选项所对应的扇形圆心角为度；（4）若该校共有 1500 名学生，请你估计该校学生“停课不停学”期间平均每天利用网络学习时间在 C 选项的有多少人？ 24．（8 分）2020 年 5 月，全国“两会”召开以后，应势复苏的“地摊经济”带来了市场新活力，小丹准备购进 A、B 两种类型的便携式风扇到地摊一条街出售．已知 2 台 A 型风扇和 5 台 B 型风扇进价共 100 元， 3 台 A 型风扇和 2 台 B 型风扇进价共 62 元．（1）求 A 型风扇、B 型风扇进货的单价各是多少元？（2）小丹准备购进这两种风扇共 100 台，根据市场调查发现，A 型风扇销售情况比 B 型风扇好，小丹准备多购进 A 型风扇，但数量不超过 B 型风扇数量的 3 倍，购进 A、B 两种风扇的总金额不超过 1170 元．根据以上信息，小丹共有哪些进货方案？ 25．（8 分）已知：如图①，将一块 45°角的直角三角板 DEF 与正方形 ABCD 的一角重合，连接 AF，CE，点 M 是 CE 的中点，连接 DM．（1）请你猜想 AF 与 DM 的数量关系是．（2）如图②，把正方形 ABCD 绕着点 D 顺时针旋转α角（0°＜α＜90°）． ①AF 与 DM 的数量关系是否仍成立，若成立，请证明；若不成立，请说明理由；（温馨提示：延长 DM 到点 N，使 MN＝DM，连接 CN） ②求证：AF⊥DM； ③ 若旋转角 α ＝ 45 ° ，且 ∠ EDM ＝ 2 ∠ MDC ，求的值．（可不写过程，直接写出结果） 26．（10 分）如图，在平面直角坐标系中，矩形 ABCD 的边 BC 与 x 轴、y 轴的交点分别为 C（8，0），B（0， 6），CD＝5，抛物线 y＝ax2﹣ x+c（a≠0）过 B，C 两点，动点 M 从点 D 开始以每秒 5 个单位长度的速

度沿 D→A→B→C 的方向运动到达 C 点后停止运动．动点 N 从点 O 以每秒 4 个单位长度的速度沿 OC 方向运动，到达 C 点后，立即返回，向 CO 方向运动，到达 O 点后，又立即返回，依此在线段 OC 上反复运动，当点 M 停止运动时，点 N 也停止运动，设运动时间为 t．（1）求抛物线的解析式；（2）求点 D 的坐标；（3）当点 M，N 同时开始运动时，若以点 M，D，C 为顶点的三角形与以点 B，O，N 为顶点的三角形相似，求 t 的值；（4）过点 D 与 x 轴平行的直线，交抛物线的对称轴于点 Q，将线段 BA 沿过点 B 的直线翻折，点 A 的对称点为 A'，求 A'Q+QN+DN 的最小值．

资料库

2020年湖南省邵阳市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料