进化算法概述进化算法概述.pdf-资料库

ELEDIA Research Center ELEDIA@UniTN ‐ University of Trento Via Sommarive 9, I‐38123 Trento, Italy E‐mail: andrea.massa@unitn.it Web: www.eledia.org/eledia‐unitn Laboratoire des Signaux et Systèmes UMR8506 (CNRS‐CENTRALE SUPELEC‐UNIV. PARIS SUD) rue Joliot‐Curie 3, 91192 Gif‐sur‐Yvette, France E‐mail: andrea.massa@l2s.centralesupelec.fr Web: www.eledia.org/eledia‐l2s Optimization Theory, Techniques, and MATLAB simulations Global (Evolutionary) Optimization Methods Prof. Andrea MASSA UESTC “2018 International Summer School” July 16‐20, 2018 – Chengdu, China Outline (1) What are EAs? What are EAs? (2) How are EAs defined? How are EAs defined? (3) Why and where using EAs? Why and where using EAs? (4) Conclusions Conclusions Copyright Notice All rights to the content of this document are reserved. Any use, in whole or in part, of the contents included in this document, including the storage, reproduction, editing, dissemination or distribution of their content through any technology platform, support, or computer network is forbidden without the prior written permission from the author. Tutti i diritti relativi ai contenuti del presente documento sono riservati. È vietato qualsiasi utilizzo, totale o parziale, dei contenuti inseriti nel presente documento, ivi inclusa la memorizzazione, riproduzione, rielaborazione, diffusione o distribuzione dei contenuti stessi mediante qualunque piattaforma tecnologica, supporto o rete telematica, senza previa autorizzazione scritta da parte dell’autore. ELEDIA Research Center – All Rights Reserved What are EAs? What are EAs? EAs are Methods for determining the Solution of Problems ... … but the Problems MUST be properly reformulated as suitable Optimization Problems Problem Problem Eating • Good meal • In a lovely place Where to go? Solution Solution Restaurant in Paris Home Restaurant in Chengdu McDonald’s ELEDIA Research Center – All Rights Reserved 3 ELEDIA Research Center – All Rights Reserved 2 4

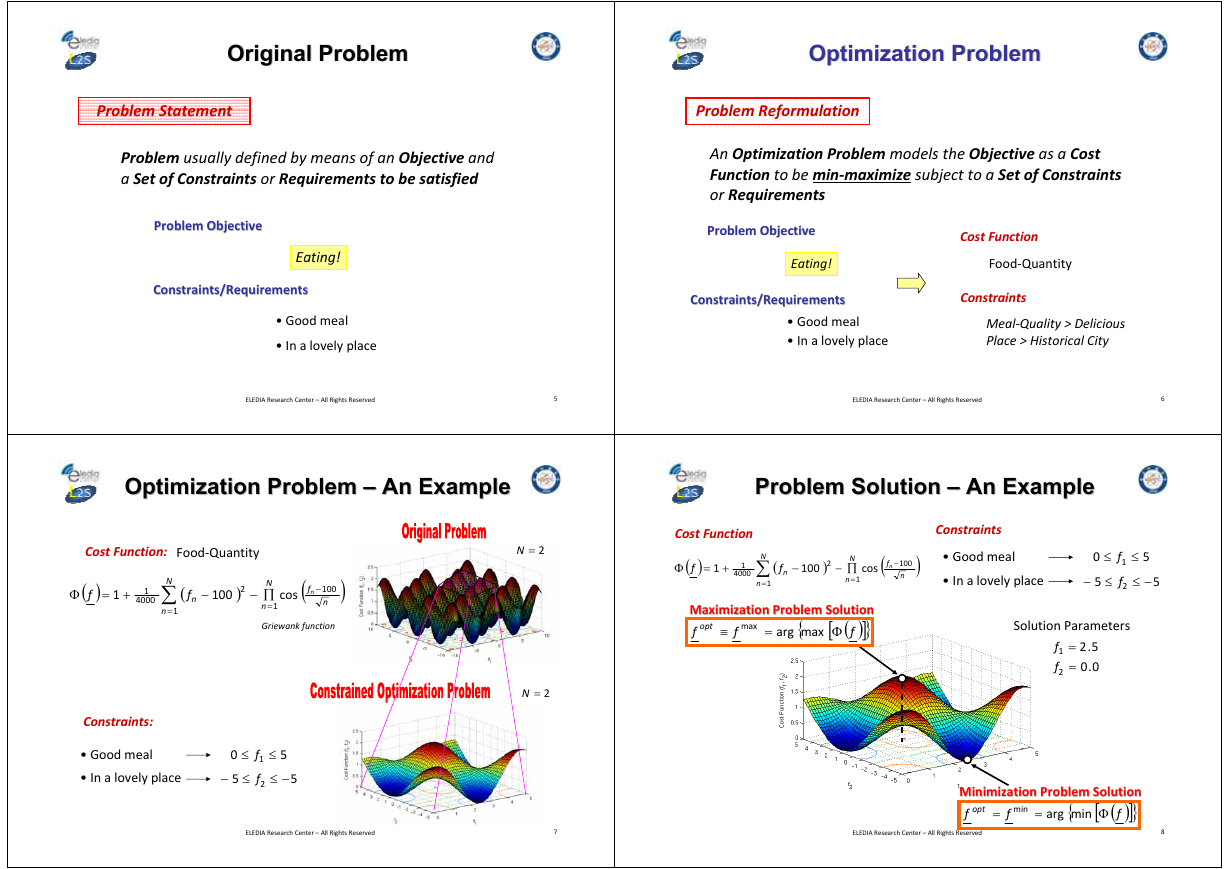
Original Problem Original Problem Optimization Problem Optimization Problem Problem Statement Problem Reformulation Problem usually defined by means of an Objective and a Set of Constraints or Requirements to be satisfied Problem Objective Problem Objective Eating! Constraints/Requirements Constraints/Requirements • Good meal • In a lovely place ELEDIA Research Center – All Rights Reserved Optimization Problem –– An Example An Example Optimization Problem Cost Function: Food‐Quantity ( ) f Φ += 1 1 4000 N ∑ n = 1 ( f n − 100 ) 2 N ∏− = n 1 cos ( − f n 100 n ) Griewank function Constraints: • Good meal • In a lovely place 0 ≤ f ≤− 5 1 ≤ f 5 −≤ 2 5 ELEDIA Research Center – All Rights Reserved 2=N 2=N 5 7 An Optimization Problem models the Objective as a Cost Function to be min‐maximize subject to a Set of Constraints or Requirements Problem Objective Problem Objective Eating! Constraints/Requirements Constraints/Requirements Cost Function Food‐Quantity Constraints • Good meal • In a lovely place Meal‐Quality > Delicious Place > Historical City ELEDIA Research Center – All Rights Reserved Problem Solution –– An Example An Example Problem Solution Cost Function ( ) f += Φ 1 1 4000 Constraints ( f n − 100 ) 2 N ∏− = n 1 cos ( − f n 100 n ) • Good meal • In a lovely place N ∑ n = 1 0 ≤ f ≤− 5 1 ≤ f 5 −≤ 2 Problem Solution Maximization Problem Solution Maximization ] ( ) }f f opt = arg { max [ Φ max ≡ f Solution Parameters f 1 f 2 = = 5.2 0.0 Problem Solution Minimization Problem Solution Minimization ] ( ) }f f opt = arg { min [ Φ min = f ELEDIA Research Center – All Rights Reserved 5 6 8

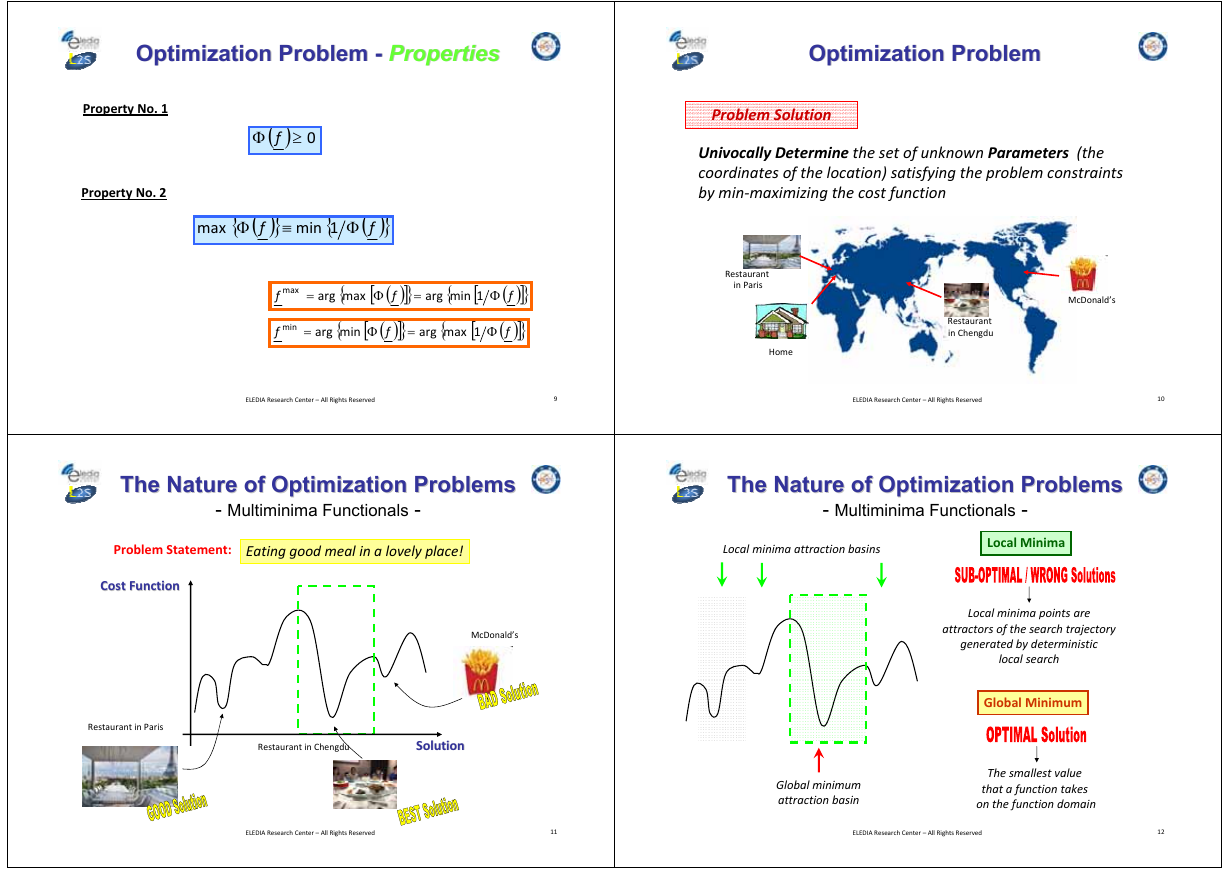
Optimization Problem Optimization Problem -- Properties Properties Optimization Problem Optimization Problem Property No. 1 Property No. 2 ( ) 0≥ Φ f max { Φ ( ) } f ≡ { 1min ( ) }f Φ Problem Solution Univocally Determine the set of unknown Parameters (the coordinates of the location) satisfying the problem constraints by min‐maximizing the cost function max = arg min = arg f f = { max [ { Φ min ] [ ( ) } Φ f ] ( ) } f [ { 1min arg [ { 1max = arg ] ( ) }f Φ ] ( ) }f Φ Restaurant in Paris Home McDonald’s Restaurant in Chengdu ELEDIA Research Center – All Rights Reserved 9 ELEDIA Research Center – All Rights Reserved 10 The Nature of Optimization Problems The Nature of Optimization Problems - Multiminima Functionals - Problem Statement: Eating good meal in a lovely place! Cost Function Cost Function McDonald’s Restaurant in Paris Restaurant in Chengdu Solution Solution The Nature of Optimization Problems The Nature of Optimization Problems - Multiminima Functionals - Local minima attraction basins Local Minima Local minima points are attractors of the search trajectory generated by deterministic local search Global Minimum Global minimum attraction basin The smallest value that a function takes on the function domain ELEDIA Research Center – All Rights Reserved 11 ELEDIA Research Center – All Rights Reserved 12

The Nature of Optimization Problems The Nature of Optimization Problems Local Minima: Benefit or Problem? Local Minima: Benefit or Problem? Two local minima are neighbors if and only if their attraction basins are neighbors Local minimum “The ensemble of the attraction basins forms the function landscape” “The values of the objective function at local minima are (generally) better than the values at the starting points” In a minimization problem, the probability of low values of the objective function is larger for local minima than for a point randomly extracted from the function landscape “In one search for low‐cost solutions, sampling local minima is more effective than sampling random points” [*] R. Battiti, et al., Reactive Search and Intelligent Optimization.Operations Research/Computer Science Interfaces Series, Vol. 45, Springer, November 2008. [*] R. Battiti, et al., Reactive Search and Intelligent Optimization.Operations Research/Computer Science Interfaces Series, Vol. 45, Springer, November 2008. ELEDIA Research Center – All Rights Reserved 13 ELEDIA Research Center – All Rights Reserved 14 Local Minima: TabuTabu Local Minima: “The memory about the previously found local minima, can be mined to produce better and better starting points” LEARNING from the previous history Iterated Search )fΦ ( Penalty Term Once the local minimum “a” is found, the penalty term allows to avoid the search in the attraction basin of “a” in the next iterations. [*] R. Battiti, et al., Reactive Search and Intelligent Optimization.Operations Research/Computer Science Interfaces Series, Vol. 45, Springer, November 2008. 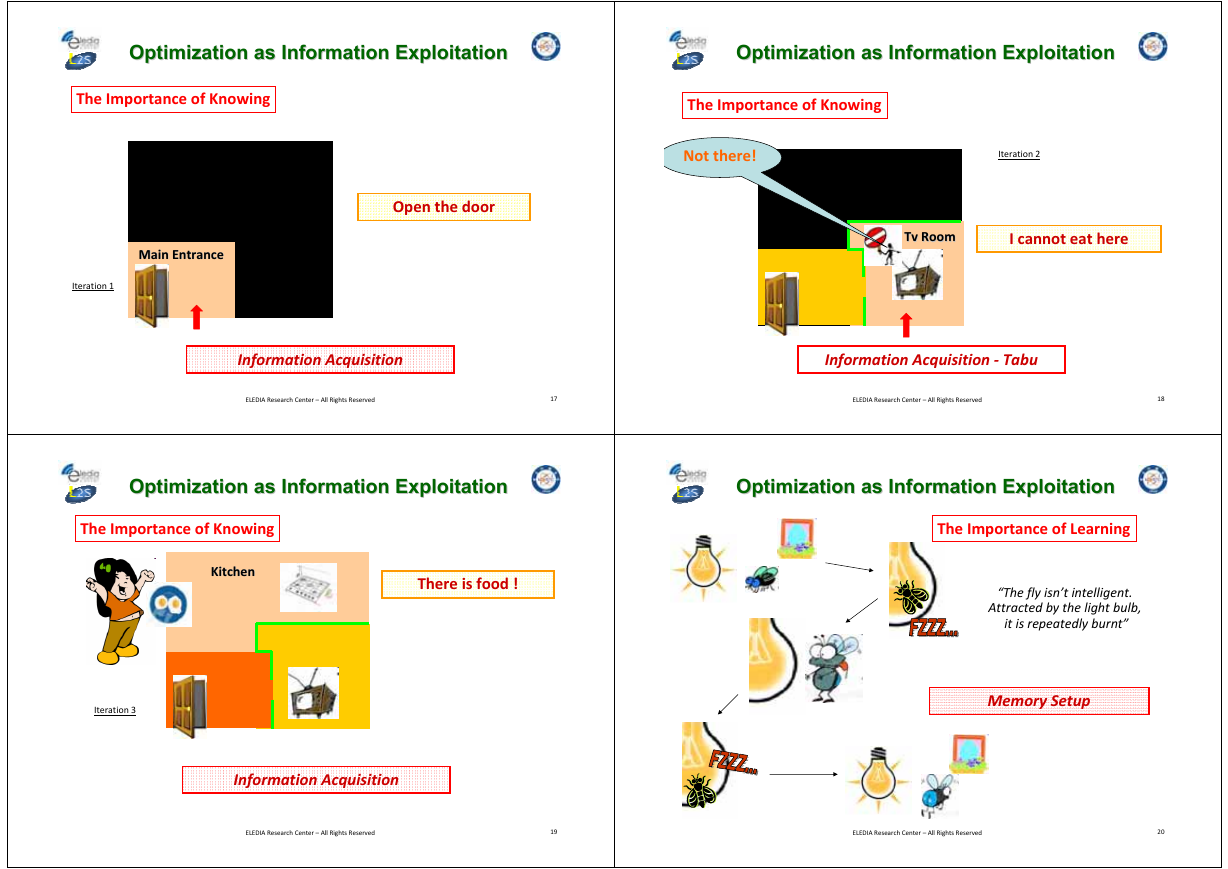f Optimization Meaning/Needs Optimization Meaning/Needs “Optimization as Information Exploitation” The Importance of Knowing Analytical framework A‐priori information Eating! “I can eat at home!” “Definition of the Boundary Landscape” Problem Bounds ELEDIA Research Center – All Rights Reserved 15 ELEDIA Research Center – All Rights Reserved 16

Optimization as Information Exploitation Optimization as Information Exploitation Optimization as Information Exploitation Optimization as Information Exploitation The Importance of Knowing The Importance of Knowing Open the door MainMain Entrance Entrance Iteration 1 Not there! Iteration 2 Tv Room Tv Room I cannot eat here Information Acquisition Information Acquisition ‐ Tabu ELEDIA Research Center – All Rights Reserved 17 ELEDIA Research Center – All Rights Reserved 18 Optimization as Information Exploitation Optimization as Information Exploitation Optimization as Information Exploitation Optimization as Information Exploitation The Importance of Knowing The Importance of Learning Kitchen Kitchen There is food ! “The fly isn’t intelligent. Attracted by the light bulb, it is repeatedly burnt” Iteration 3 Memory Setup Information Acquisition ELEDIA Research Center – All Rights Reserved 19 ELEDIA Research Center – All Rights Reserved 20

The Importance of Information The Importance of Information “Human problem solving is strongly connected to learning. Learning takes places when the problem at hand is not well known at the beginning, and its structure becomes more and more clear when more experience with the problem is available” Information Exploitation Define the Bounds of the Problem Landscape Memory Setup Knowing Problem Landscape [*] R. Battiti et al., Reactive Search and Intelligent Optimization.Operations Research/Computer Science Interfaces Series, Vol. 45, Springer, November 2008. EAs as …… Information Exploitation Information Exploitation EAs as Tools Tools Optimization Methods Local Techniques Conjugate Gradient Methods Quasi‐Newton Methods Convex Programming Linear Programming Greedy Algorithm Global Techniques Random Walk Simulated Annealing (SA) Tabu Search Genetic Algorithms (GAs) Memetic Algorithm (MA) Differential Evolution (DE) Particle Swarm (PSO) Ant Colony (ACO) Bacteria Foraging (BF) } Single Agent Multiple Agent (EAs) ELEDIA Research Center – All Rights Reserved 21 ELEDIA Research Center – All Rights Reserved 22 Local vs. Global Approaches Local vs. Global Approaches Which initial locations are suitable to reach the global minimum? Local Techniques Local Techniques Initialization (k=0): Guess (approximate) solution ) af ( 0 Iterative Procedure: f a ( =+ k ) 1 f ) a ( k + s k k ,...,1= K Global Search Algorithms Algorithms able to escape from local minima points Local Search Algorithms Algorithms which only exploring the neighborhood of a local minimum point Local strategies can reach the global optimum if and only if Local strategies can reach the global optimum if and only if their their search starts in the attraction basin of the global optimum search starts in the attraction basin of the global optimum s α= k k d k kα Step Length kd Search Direction ( )0>kα Approaches: Steepest Descent Method Conjugate Gradient Method ELEDIA Research Center – All Rights Reserved 23 ELEDIA Research Center – All Rights Reserved 24

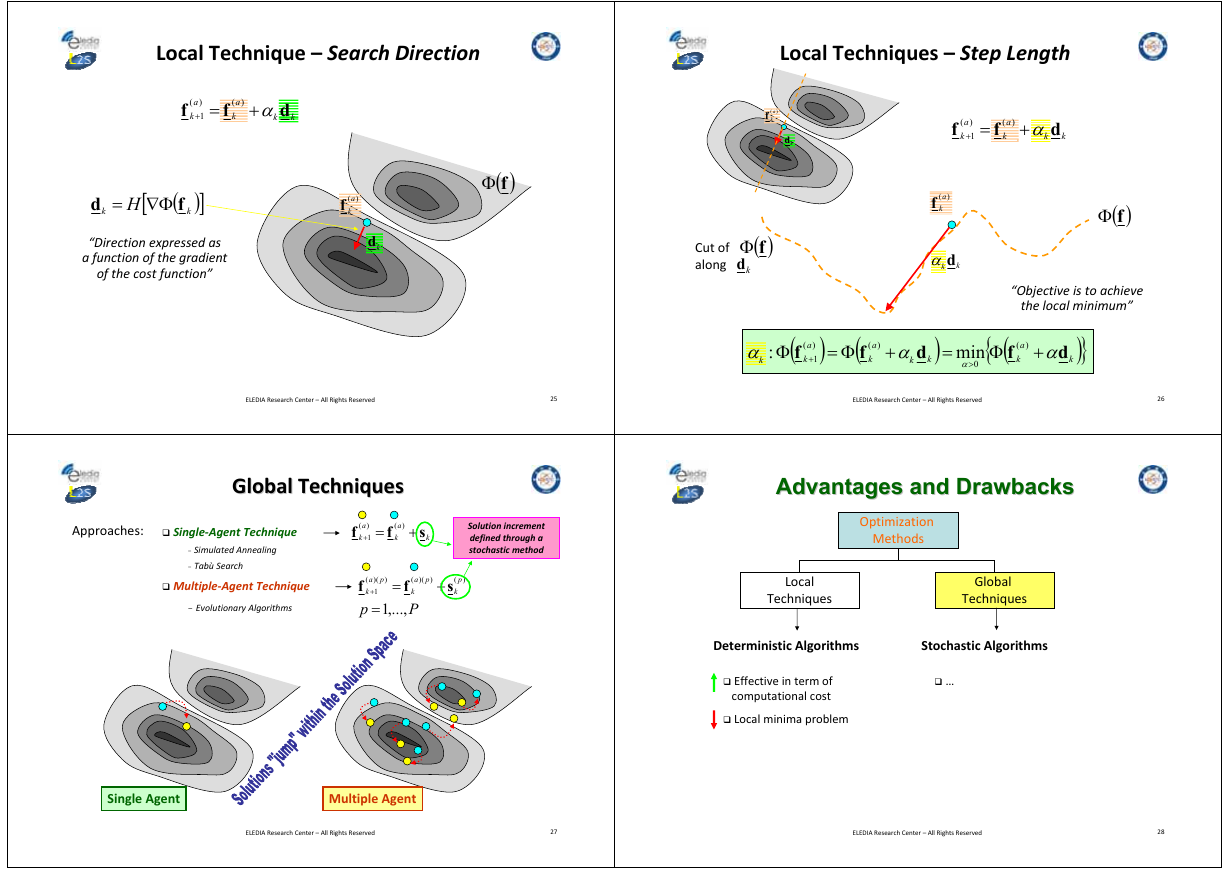
Local Technique – Search Direction Local Techniques – Step Length f a ( =+ k ) 1 f ) a ( k α+ k d k d ( f k H Φ∇= [ ]k ) “Direction expressed as a function of the gradient of the cost function” ( )fΦ ) (a kf kd ) (a kf kd f a ( =+ k ) 1 f ) a ( k α+ k d k Cut of along ( )fΦ kd ) (a kf kdα k α k : Φ ( f ) a ( ) k 1 + ( f Φ= ) a ( k + α k d k ) = { min Φ α > 0 ( )fΦ “Objective is to achieve the local minimum” ( f ) a ( k + d α ) }k ELEDIA Research Center – All Rights Reserved 25 ELEDIA Research Center – All Rights Reserved 26 Global Techniques Global Techniques Approaches: Single‐Agent Technique f - Simulated Annealing - Tabù Search Multiple‐Agent Technique - Evolutionary Algorithms a ( k ) 1 =+ f ) a ( k + s k Solution increment defined through a stochastic method ) f p pa )( ( k 1 + = f = ,...,1 ) pa )( ( k p ) + s ( k P Advantages and Drawbacks Advantages and Drawbacks Optimization Methods Local Techniques Global Techniques Deterministic Algorithms Stochastic Algorithms Effective in term of computational cost Local minima problem … Single Agent Multiple Agent ELEDIA Research Center – All Rights Reserved 27 ELEDIA Research Center – All Rights Reserved 28

Advantages of EAs Advantages of EAs Global search Hill‐climbing features (no local “minima” problem) No differentiation Straightforward introduction of a‐priori information (or constraints) Discrete / continuous space Intrinsically parallel computing Hybridization with deterministic procedures Drawbacks: Computational load Low convergence rate Do they exist? How to mitigate? EAs as Optimal/General Purpose Tools? The “Holy Grail” for Problem Optimization? ELEDIA Research Center – All Rights Reserved 29 ELEDIA Research Center – All Rights Reserved 30 Optimization Paradigms Optimization Paradigms “Which Algorithm is More Suitable for the Solution of an Optimization Problems?” DE GAs PSO “The Lunch is No‐Free” [*] ACO MA BF … Optimization Theorems Optimization Theorems Theorem 1 [*] Algorithms Problems “The average performance of any pair of algorithms across all possible problems is identical” Implication: Representative Example “If an algorithm performs better than random search on some class of problems then in must perform worse than random search on the remaining problems” [*] D.H. Wolpert et al., IEEE Trans. Evol. Comput., vol. 1, no. 1, pp. 67‐82, Apr.1997. [*] D.H. Wolpert et al., IEEE Trans. Evol. Comput., vol. 1, no. 1, pp. 67‐82, Apr.1997. ELEDIA Research Center – All Rights Reserved 31 ELEDIA Research Center – All Rights Reserved 32

资料库

进化算法概述进化算法概述.pdf

相关推荐

大数据

热门标签

最新资料