软阈值函数学习笔记：理论推导、案例详解、代码.pdf-资料库

signalproc8848-12631236-16359647239591924616.pdf-第1页.png

第1页 / 共10页

signalproc8848-12631236-16359647239591924616.pdf-第2页.png

第2页 / 共10页

signalproc8848-12631236-16359647239591924616.pdf-第3页.png

第3页 / 共10页

signalproc8848-12631236-16359647239591924616.pdf-第4页.png

第4页 / 共10页

signalproc8848-12631236-16359647239591924616.pdf-第5页.png

第5页 / 共10页

signalproc8848-12631236-16359647239591924616.pdf-第6页.png

第6页 / 共10页

signalproc8848-12631236-16359647239591924616.pdf-第7页.png

第7页 / 共10页

signalproc8848-12631236-16359647239591924616.pdf-第8页.png

第8页 / 共10页

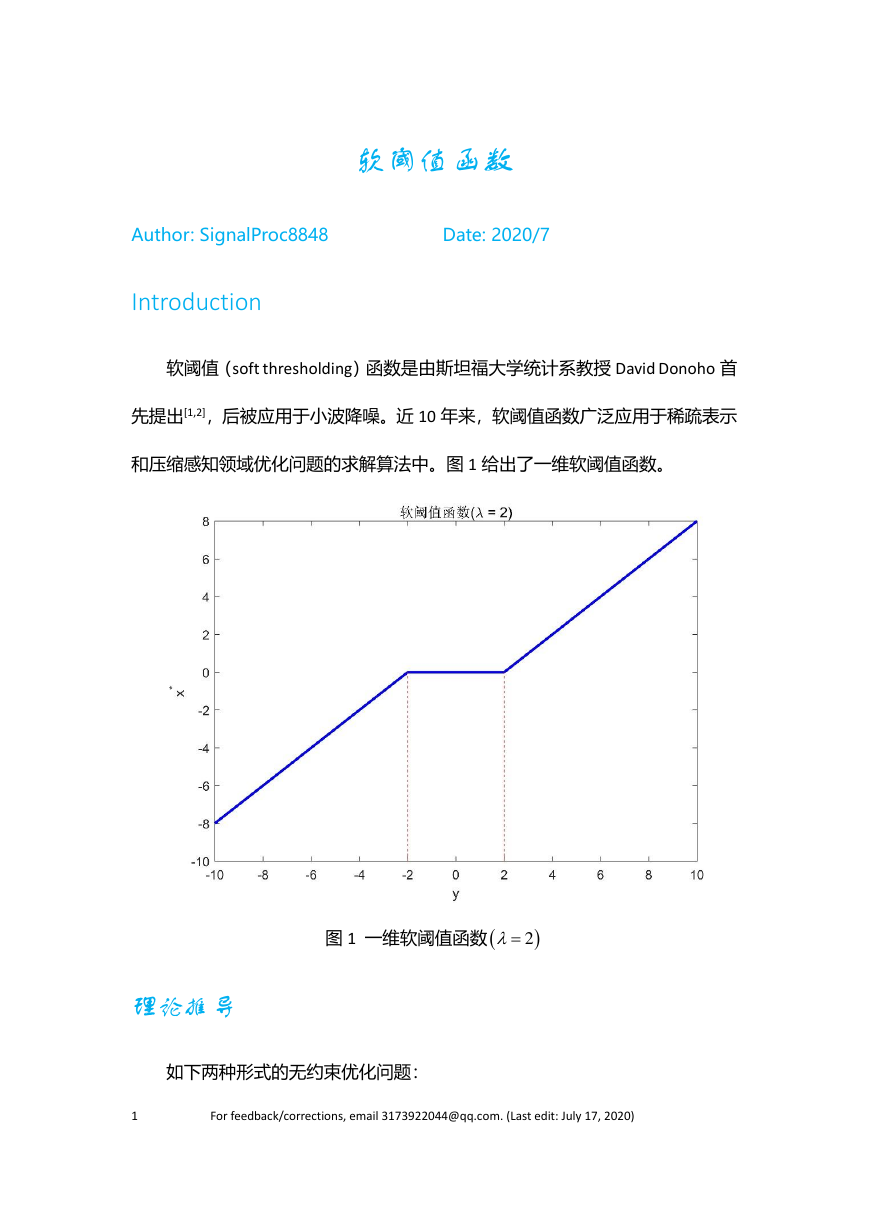
软阈值函数 Author: SignalProc8848 Date: 2020/7 Introduction 软阈值（soft thresholding）函数是由斯坦福大学统计系教授 David Donoho 首先提出[1,2]，后被应用于小波降噪。近 10 年来，软阈值函数广泛应用于稀疏表示和压缩感知领域优化问题的求解算法中。图 1 给出了一维软阈值函数。图 1 一维软阈值函数理论推导如下两种形式的无约束优化问题： 1 For feedback/corrections, email 3173922044@qq.com. (Last edit: July 17, 2020) ()2=

（1）（2）式中， —n 维优化变量，； —给定的 n 维向量，； —罚参数，； —向量的范数，； —向量的范数，；式（1）—（2）是等价的，下面的推导都采用式（2），这是因为式（2）是范数的近邻映射[3]。式（2）中优化变量，因此这是一个 N 维无约束优化问题。巧妙利用范数和范数平方和的分离特性，可将 N 维优化问题转化为 N 个一维优化问题，从而显著降低原问题的难度。依照上述分析，式（2）可作如下变形（3） 2 For feedback/corrections, email 3173922044@qq.com. (Last edit: July 17, 2020) 2211argmin2n−+xxyx2121argmin2n+−xxxyxnxyny01xx1l11niix==x2xx2l()12221niix==x1lnx1l2l()()()()()12122122,,112,,1211argmin21argmin21argmin21argmin2nninniiixxxiiniiixxxiniiixixxyxxyxxy=====+−=+−=+−=+−xxxxy

（4）式（3）中，极小值与求和作了交换，简化了问题，相对于问题（2），问题（4）是 N 个独立的一维优化问题，处理起来简单的多。此处蕴含着一个重要的数学思想：运算次序交换，如极限与微分交换次序、极限与积分交换次序、积分与微分交换次序、积分交换次序等。不失一般性，我们首先讨论如下一维优化问题式中，（5） —优化变量，，是向量的一个分量； —给定的常数，，是向量的一个分量； —罚参数，，与式（2）中的罚参数一样；在上连续，且严格凸，仅在处不可导。这意味着问题（5）有且仅有一个最小值点。由极值存在的必要条件，对目标函数求导，并令导数等于 0，得到极值点（6a）（6b） 3 For feedback/corrections, email 3173922044@qq.com. (Last edit: July 17, 2020) ()()()122111222221argmin21argmin21argmin2nxxnnnxxxyxxyxxy+−+−=+−x()()21argmin2xfxxxy=+−xxxyyy0()fx0x=()fxx()()()1sgndfxxxydx=+−()()()1sgn0sgnxxyxyx+−==−

（6c）式（6b）的等号右边仍含有变量，需要分情况讨论。时，，则 1）当 ①若即，，则在取得极小值，（7） ②若，则，，矛盾。通过导数观察在区上的单调性，即间（8）则在上单调递减，再由的连续性可知，在处取得极小值，即比较和当（9）（ 10 ）时，综合①和②，在上的最小值点为。 2）当时 ①若，则，，矛盾。通过导数观察在区间上的单调性，即（11） 4 For feedback/corrections, email 3173922044@qq.com. (Last edit: July 17, 2020) ()1,0sgn1,0xxx=−x0y()0,x+()sgn1x=0xy=−()fxxy=−()21122fxyy=−+=−(),0x−()sgn1x=−0xy=+()fx(),0−()()110dfxxydx=−+−()fx(),0−()fx()fx0x=()2102fy=()fx()0f()()()()222211110202222fxfyyyyy−=−−=−+−=−−0y()fxxxy=−y−()0,x+()sgn1x=20xy=−−()fx()0,+()()110dfxxydx=+−

则在上单调递增，再由的连续性可知，在处取得极小值，即（12） ②若，则，，则在取得极小值，（13）（14）即比较和当 3）当 ①若时，综合①和②，在上的最小值点为。时，，则，，矛盾。通过导数观察在区间上的单调性，即（15）则在上单调递增，再由的连续性可知，在处取得极小值，即（16） ②若，则，，矛盾。通过导数观察在区上的单调性，即间（17）则在上单调递减，再由的连续性可知，在处取得极 5 For feedback/corrections, email 3173922044@qq.com. (Last edit: July 17, 2020) ()fx()0,+()fx()fx0x=()2102fy=(),0x−()sgn1x=−0xy=+()fxxy=+()21122fxyy=++=−−()fx()0f()()()()222211110202222fxfyyyyy−=−−−=−++=−+y−()fxxxy=+y−()0,x+()sgn1x=0xy=−()fx()0,+()()()11110dfxxyxydx=+−=+−()fx()0,+()fx()fx0x=()2102fy=(),0x−()sgn1x=−0xy=+()fx()0,+()()()11110dfxxyxydx=−+−=+−−()fx(),0−()fx()fx0x=

小值，即（18）综合①和②，当时，在上的最小值点为综合 1）、2）和 3）三种情形，可得（19）若将式（19）中的视为变量，视为阈值，上式即为一维软阈值(soft thresholding) 公式。案例 1、若，，那么优化问题（2）的解为多少？解析：的任意分量都大于阈值，即所有分量均落入内。由式（19）可知，所以，同理可得，，，综上所述，优化问题（2）的解为 2、若，，那么优化问题（2）的解为多少？解析：的任意分量都小于，即所有分量均落入这区间内。由式（19）可知，，同理可得，，。综上所述，优化问题（2）的解为 6 For feedback/corrections, email 3173922044@qq.com. (Last edit: July 17, 2020) ()2102fy=y−()fxx0x=()()2,1argmin0,2,xyyfxxxyyyy−=+−=+−y1234Ty= 0.5=xy0.5=()2.5,+110.510.50.5=−=−=xy21.5=x32.5=x43.5=xx0.51.52.53.5=x1234T−−−−y= 0.5=xy0.5−(),0.5−−110.510.50.5=+=−+=−xy21.5=−x32.5=−x43.5=−xx

. 3、若，，那么优化问题（2）的解为多少？解析：的第 1 分量和第 2 分量落入内，由式（19）可知，；的第 3 分量落入，则；的第 4 分量落入，则。综上所述，优化问题（2）的解为。 Matlab 代码软阈值冗长的推导过程使人心很累，但软阈值的 Matlab 代码却如此简单，以至于可以用一句代码去实现问题（2） function [ soft_thresh ] = softThreshold(y,lambda) soft_thresh = sign(y).*max(abs(y) - lambda,0); end 代码中是 n 维向量，是标量，表示向量与标量作差，线性代数老师可从没教过啊，令人费解。Matlab 软件中约定表示向量的每个分量都与作差，结果是与同维度的向量。读者可在 Matlab 中作简单试验，予以验证。为了便于读者理解软阈值的 Matlab 代码，我将式（19）作如下变形（20） 7 For feedback/corrections, email 3173922044@qq.com. (Last edit: July 17, 2020) 0.51.52.53.5−−=−−x1234T−y= 2.5=xy()2.5,2.5−120==xxy()2.5,+30.5=xy(),2.5−−41.5=−xx000.51.5=−xy−y−yyy()2(),1argmin0,2(),xyabsyyxxyyyabsyy−=−+−=+=−−−

式（20）中，和这两种情况仅相差一个负号，对应 Matlab 代码中的 sign(y)函数，sign(y)表示对向量 y 中各分量符号的判断。总结 1）软阈值函数其实就是的 Moreau 包络，而是近邻算子。关于 Moreau 包括和近邻算子的详细内容参考文献[3]。 2）优化问题（2）与基追踪降噪问题（21）非常相似，却不解决基追踪降噪问题式中，（21） — 矩阵；稀疏表示中称作过完备词典，通常要求； —稀疏表示系数，；文献[4]对此作了说明:由于矩阵的存在，破坏了范数的分离的特性，其实就是的各分量经过的线性组合后，再平方会出现分量间的交叉项，造成变量不能像式（3）那样可分离。 3）软阈值函数是分裂增广拉格朗收缩算法（split augmented Lagrangian shrinkage algorithm）[5]变量更新的关键一步，深入理解软阈值函数是学习后续稀疏优化算法的基础。 8 For feedback/corrections, email 3173922044@qq.com. (Last edit: July 17, 2020) 0y0y−()21212fx=+−xxy1x()12,121argmin2nproy=+−xxxxy1x2211argmin2nD−+xxDnmmnmD2lD

资料库

软阈值函数学习笔记：理论推导、案例详解、代码.pdf

相关推荐

大数据

热门标签

最新资料