logo资料库

2012全国大学生数学建模全国一等奖_葡萄酒的评价.doc

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：0.87M 资料格式：doc 举报 版权申诉
第1页 / 共32页
第2页 / 共32页
第3页 / 共32页
第4页 / 共32页
第5页 / 共32页
第6页 / 共32页
第7页 / 共32页
第8页 / 共32页
资料共32页，剩余部分请下载后查看
    方差检验模型 灰色关联分析法 多元数据的相关性分析 二元线性回归模型
    二、问题分析
    【2】
    2012 高教社杯全国大学生数学建模竞赛 承 诺 书 我们仔细阅读了中国大学生数学建模竞赛的竞赛规则. 我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮 件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问 题。 我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他 公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正 文引用处和参考文献中明确列出。 我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。如有违反 竞赛规则的行为，我们将受到严肃处理。 我们授权全国大学生数学建模竞赛组委会，可将我们的论文以任何形式进行 公开展示（包括进行网上公示，在书籍、期刊和其他媒体进行正式或非正式发表 等）。 我们参赛选择的题号是（从 A/B/C/D 中选择一项填写）： A 我们的参赛报名号为（如果赛区设置报名号的话）： 所属学校（请填写完整的全名）： 辽宁省大连海事大学 参赛队员 (打印并签名) ：1. 2. 3. 指导教师或指导教师组负责人 (打印并签名)： 日期： 年 月 日 赛区评阅编号（由赛区组委会评阅前进行编号）：
    2012 高教社杯全国大学生数学建模竞赛 编 号 专 用 页 赛区评阅编号（由赛区组委会评阅前进行编号）： 赛区评阅记录（可供赛区评阅时使用）： 全国统一编号（由赛区组委会送交全国前编号）： 全国评阅编号（由全国组委会评阅前进行编号）： 评 阅 人 评 分 备 注 2
    葡萄酒的评价 摘要 葡萄酒质量的评定一般是由有资质评酒员在对葡萄酒进行品尝后分类指标 打分，然后求和得到其总分而确定，酿酒葡萄的好坏与所酿葡萄酒的质量有直接 的关系，葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的 质量。我们将本题归为对大量数据分析整理的统计问题，采用方差检验、灰色关 联、数据样本统计分析、二元线性回归模型等数学方法进行分析得到预期结果。 对于问题一，我们将两组评酒员对酒的评价结果有无显著性差异的问题， 转化为两组评酒员这一因素对酒的评分的影响是否显著的问题，若影响不显著则 说明两组评酒员的评分实质上无显著性差异，据此建立方差检验模型，构造一个 F 变量，通过假设检验来确定两组评酒员对酒的评价结果有无显著性差异，由于 酒的选取是随机的，所以可以用标准差这一统计数值表来表示两组评酒员评分的 波动性，波动性越小，评分结果越可靠。 对于问题二，首先选出与评价方面最为相关的理化指标，用变异系数法计 算出每一种理化指标的权重，再用均值化无差异法对理化指标进行处理，得出各 种葡萄理化指标的综合评分，并再次将其与葡萄酒的评分均值化无差异化处理， 将结果求和得到每一种葡萄质量的评分，重新排序后，用 Excel 模拟出序号与葡 萄质量评分的曲线图，将位于同一高度的序号划分为一级，由此得出葡萄的分类 级别。 对于问题三，对酿酒葡萄与葡萄酒的理化指标的关系这一问题，我们分类 讨论，对于葡萄酒色泽理化指标，我们查得其实质是与葡萄样品花色苷和单宁两 个理化指标有关的，因此运用灰色关联分析法分析每一个因素对葡萄酒色泽的影 响，并采用优势比较法，分析出哪一因素对葡萄酒色泽这一理化指标更有影响。 关于葡萄酒样品中除色泽以外的其它理化指标，都可以在葡萄样品中找到相应的 理化指标与之一一对应，因此算出葡萄酒样品与酿酒葡萄样品理化指标之间的相 关系数，从而说明它们之间的联系。 对于问题四，由于在问题二中已对酿酒葡萄的理化指标进行了综合分析并 给出了一个质量分数，所以酿酒葡萄可用问题二中给出的质量分数来分析。对于 葡萄酒的理化指标的分析，我们采用问题二中提出的综合评分法，基于葡萄酒的 理化指标对其样品给出一个分数，作为另一个影响葡萄酒质量的因素，从而变成 二元线性回归模型。建立二元线性回归模型，用 matlab 软件将得到的评酒员对 葡萄酒的评分、葡萄样品的评分、葡萄酒样品评分三者带入方程中，确定回归系 数并进行检验，从而分析出葡萄酒的质量是否可以用酿酒葡萄与葡萄酒的理化指 标来衡量。 关键词 方差检验模型 灰色关联分析法 多元数据的相关性分析 二元线性 回归模型 变异系数法 均值化无差异法 3
    一、问题重述 葡萄酒质量的评定一般是让有资质评酒员在对葡萄酒进行品尝后对其分 类指标打分，然后求和得到其总分，从而确定葡萄酒的质量。酿酒葡萄的好坏与 所酿葡萄酒的质量有直接的关系，葡萄酒和酿酒葡萄检测的理化指标会在一定程 度上反映葡萄酒和葡萄的质量。 （1）附件一中给出了两组评酒员共 20 人对某一年份红葡萄酒和白葡萄酒 的打分，取样总共 27 份红葡萄酒和 28 份白葡萄酒，试分析两组评酒员的评价结 果有无显著性差异，哪一组结果更可信； （2）附件 2 和附件 3 分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数 据，根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。 （3）分析酿酒葡萄与葡萄酒的理化指标之间的联系。 （4）分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响，并论证能否 用葡萄和葡萄酒的理化指标来评价葡萄酒的质量？ 二、问题分析 本题第一问采用的方法是方差检验的方法，由于 27 种红葡萄酒样品和 28 种白葡萄酒样品是随机选取的，所以两组评酒员对 27 种红葡萄酒样品和 28 种白 葡萄酒样品的评分也认为是随机的，并且服从正态分布，要分析他们两组评酒员 的评价结果是否有显著性差异，就要用到假设检验的方法，构造一个 F 检验的模 型，通过分析计算出的 AF 与 关系，来判断两组评 , a DF e DF a DF , e F 01.0 ( (05.0 F DF ) 和 ) 酒员的评价结果到底有无显著性差异，可信度的分析可以采用标准差来分析，标 准差较小，评分的波动较小，结果也就更可信一些。 由第一问得出评酒员对葡萄酒样品的评分，作为所酿葡萄酒的质量的指标。 葡萄的理化指标较多，从影响所酿葡萄酒的各个评价方面出发，选取与之联系最 为相关的理化指标作为葡萄的理化指标的评价方面。采用变异系数法算出各个指 标的权重，再采用均值化无差异法对原始指标进行标准化，根据标准化的指标数 据和各个指标的权重，计算出每一种葡萄的理化指标的综合评分，作为葡萄理化 指标的评价指标。以葡萄的理化指标的综合评分和所酿葡萄酒的评分为基础，进 行标准化，采用两组指标的和作为该种葡萄的质量的评分，对这些葡萄的评分按 从大到小的顺序进行重新排序，用 Excel 做出排序号与葡萄的质量评分的曲线 图，将位于同一高度的序号分为一个等级，再根据序号与葡萄种类的对应关系， 对每一种葡萄进行分级。 第三问的分析酿酒葡萄与葡萄酒的理化指标之间的联系，采用了灰度关联分 析法和数字特征分析法，通过资料查询我们知道葡萄酒的色泽主要与葡萄中的花 色苷和单宁有关，在分析色泽这一指标时我们采用了灰度关联分析法求出葡萄酒 的色泽与葡萄中的花色苷和单宁的联系系数，对所有数据取平均就求出相关系 数，并通过比较相关系数的大小找出影响色泽的优势因素。在分析其它指标时我 们采用了数字特征分析法，通过计算相关系数确定葡萄与葡萄酒的理化指标之间 的联系。 4
    问题四中葡萄酒的质量可以用在问题一中的评分进行衡量，而酿酒葡萄在 问题二中的求解中也给出了一个评分来衡量质量的好坏，因此此题的关键就是对 葡萄酒的理化指标的处理，由于葡萄的理化指标多而复杂，在进行回归分析的时 候，未免太过复杂，考虑到葡萄酒理化指标和酿酒葡萄的理化指标之间存在一定 相似性，因此葡萄酒的理化指标也可采用变异系数法进行一个评分，从而化简成 葡萄的质量与这两个评分之间的关系，对它们进行二元线性回归分析，并进行检 验，从而论证出葡萄的质量可否用酿酒葡萄和葡萄的理化指标来衡量。 三、模型假设与符号说明 一、模型假设 （1）评酒员对葡萄酒样品的评分是随机的，不含任何自己的主观意见。 (2)由于葡萄的理化指标的评价与所酿葡萄酒的质量对葡萄的质量都有影响， 且无法判断两者之间的重要性，可假设两者对葡萄的质量的影响程度是相同的。 （3）假设红、白葡萄样品和红、白葡萄酒样品的选取是随机的，且其理化指 标数据是服从正态分布的。 （4）在计算得到相关数据前，假设葡萄酒样品中理化指标含量的来源都是来 自于葡萄样品本身的，不考虑人工添加成分。 二、符号说明 iV 第 i 个因素的变异系数即标准差系数 Δi ix 第 i 个因素的标准差 第 i 个因素的平均数 第 i 种指标的权重 第 i 种葡萄的理化指标所构成的向量 （i=1、2·······26）  、 2S  由向量 1S 第 i 种葡萄的第 j 种理化因素  ······· 26S 构造成的矩阵 （i=1、2·······27） 第 i 种葡萄对应的葡萄酒的评分与理化指标 Wi  iS A Xij  B 5 各个指标的权重构造成的向量 第 i 种葡萄的综合得分为 Gi  iZ 的评分构成的向量。 Yij SST SSA SSE Dft Dfa Dfe  ki 第 i 种葡萄的第 j（j=1,2）个指标 总的离差平方和 组间离差平方和 组内的离差平方和 总自由度 组间自由度 组内自由度 第 k 个样本比较曲线 ix 与参考曲线 0x 的相对差值
    ir0 第 i 组数据相对第一组数据的相关系数 四、模型的建立和求解 4.1 模型一：两组评酒员的评价结果显著性差异的比较和可信度比较 对第一问可以采取 F 检验的方法 假设每一个评酒员的评分都是随机的且 服从正态分布，在方差检验中，通常，若 FA>F（Dfa，Dfe）就称某因素对试验验 结果有非常显著的影响;若 F 05.0 ( DF a , DF e )  F A  F 01.0 ( DF a , DF e ) ，则表示某因素对 试验结果有显著影响;若 F  A F 05.0 ( DF a , DF e ) ，则表示某因素对试验结果的影响不 显著。 由此思路，可以把组别作为影响酒的品质（即评分）的因素，若求出该因素 对酒的评分有十分显著或显著的影响，可以说明他们的评分是有十分显著或显著 的差异的，否则，由于两组评酒员的评分没有显著性差异，组别这一因素就不可 能对评分造成十分显著或显著的影响，所以可以用 F 检验先求出两组评酒员这一 因素对评分的影响，进而求出他们做出的评分有无显著性差异。以下用 F 检验计 算两组数据结果差异的显著性。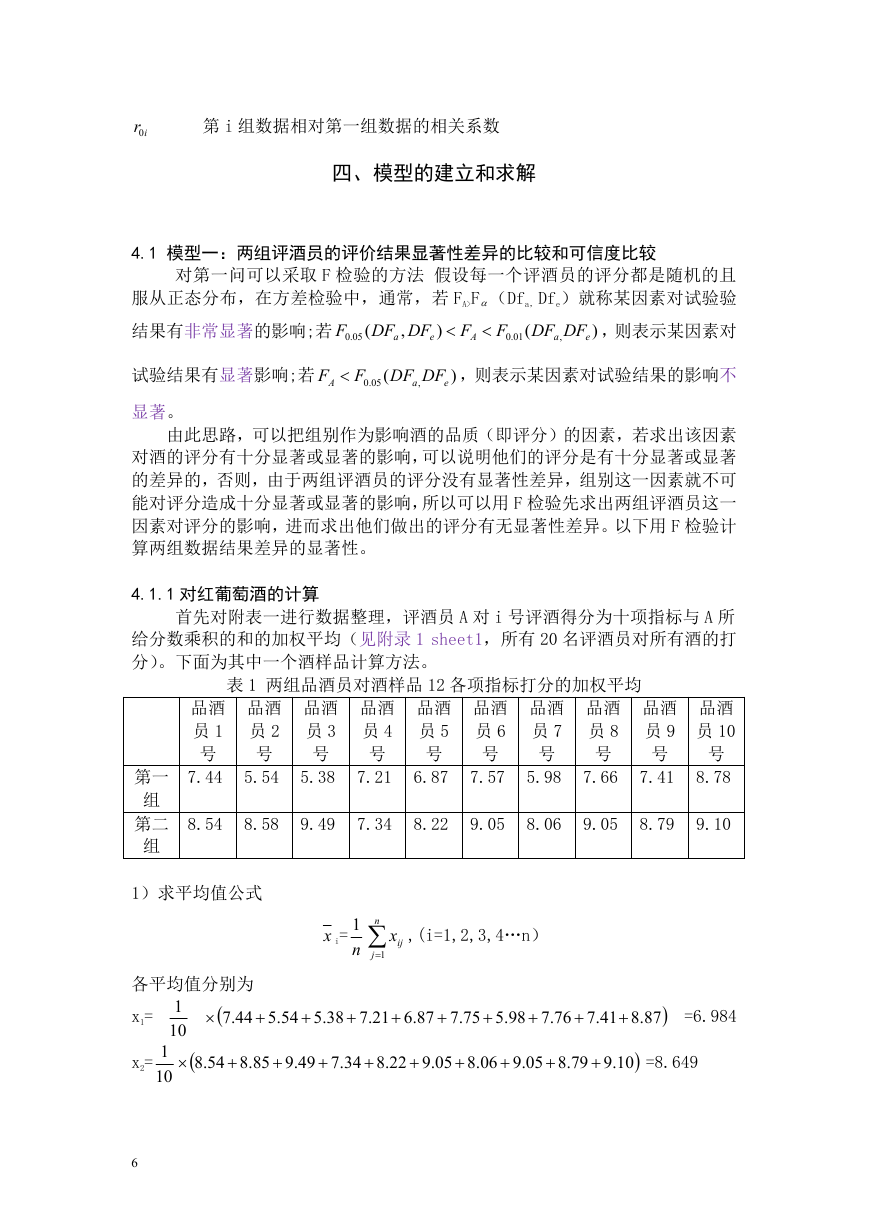 4.1.1 对红葡萄酒的计算 首先对附表一进行数据整理，评酒员 A 对 i 号评酒得分为十项指标与 A 所 给分数乘积的和的加权平均（见附录 1 sheet1，所有 20 名评酒员对所有酒的打 分）。下面为其中一个酒样品计算方法。 表 1 两组品酒员对酒样品 12 各项指标打分的加权平均 品酒 员 1 号 7.44 品酒 员 2 号 5.54 品酒 员 3 号 5.38 品酒 员 4 号 7.21 品酒 员 5 号 6.87 品酒 员 6 号 7.57 品酒 员 7 号 5.98 品酒 员 8 号 7.66 品酒 员 9 号 7.41 品酒 员 10 号 8.78 第一 组 第二 8.54 8.58 9.49 7.34 8.22 9.05 8.06 9.05 8.79 9.10 组 1）求平均值公式 各平均值分别为 x i= 1  n 1  n j ijx ,(i=1,2,3,4…n）  44.7   54.5  38.5  21.7  87.6  75.7  98.5  76.7  41.7  87.8 =6.984  54.8  85.8  49.9  34.7  22.8  05.9  06.8  05.9  79.8  10.9 =8.649 x1= x2= 1 10  1 10 6
    总的平均值为 x =  .6  984  .8 649  =7.817 1 2 2）总的离差平方和 总的离差平方和用 SST 表示，其计算式为 r SST= n  i 1  j 1   x ij 2   x 可计算得 SST=50.68661 组间离差平方和 各组间的离差平方和用 SSA 表示，其计算式为 SSA=  x i 2  x r  i 1  可计算得 SSA=13.66784 组内离差平方和 组内的离差平方和用 SSE 表示，其计算式为  SSE=   x ji  x i 2 n r i 1  j 1  可计算得 SSE=37.01877 3）计算自由度 SST 的自由度为总自由度 Dft=n-1=10-1=9 SSA 对应的自由度为组间自由度 Dfa=r-1=2-1=1 SSE 对应的自由度为组内自由度 Dfe=n-r=10-2=8 4）计算平均平方 用离差平方和除以对应的自由度即可得到平均平方，简称均方 MSA= MSE= SS A DF A SS E DF E 可计算得 MSA=13.66784 MSE=40627346 5）F 检验 组间均方和组内均方之比 F 是一个统计量，即： FA= MS MS A E 计算可得 FA=2.95 FA 服从自由度为（Dfa，Dfe）的 F 分布，对于给定的显著水平α，从任意的 F 分布表查得 F（Dfa，Dfe），如果根据数据得出的 FA>F（Dfa，Dfe）,则认为两个 7
    组对实验结果的分析有显著差异. 结果可以得到如下的表格 2 表 2 两组品酒员对 15 号红葡萄酒方差分析表 方差来源 平方和 自由度 均方 两组品酒员 13.66784 随机误差 37.01877 50.68661 总和 1 8 9 13.66784 4.627334 F 2.95 显著性 无显著差异 查表得 F0.05(1,8)=5.32>2.95 所以我们认为在 15 号红葡萄酒样品上两组数据无显著差异，不能根据单一 数据对两个评酒员评价结果的差异显著性做出结论。因此用同样的方法计算两组 品酒师对所有红葡萄酒评分的均值的差异显著性可得数据如下表 3 所示 表 3 两组品酒员对所有红葡萄酒方差分析表 方差来源 平方和 两组品酒员 0.4599 随机误差 3.67885 总和 4.13879 查表得 F0.05(1,8)=5.32>1.0002，所以我们认为在红葡萄酒的评价过程中两组评 酒员的结果是无显著性差异的 自由度 1 8 9 显著性 无显著差异 均方 0.4599 0.4598 F 1.0002 4.1.2 对白葡萄酒的分析 采用同样的方法对 15 号白葡萄酒分析可得如下表格 4 表格 4 两组品酒员对 15 号白葡萄酒方差分析表 方差来源 平方和 两组品酒员 2.178 随机误差 49.04758 总和 51.22558 查表得 F0.05(1,8)=5.32>0.3774，所以我们认为在 15 号白葡萄酒样本上俩组数据 无显著差异 自由度 1 8 9 均方 2.178 5.77047 显著性 无显著差异 F 0.3774 同样地，我们也不能根据单一数据对两个评酒员评价结果的差异显著性做出 结论，因此用同样的方法计算两组评酒师对白葡萄酒评分均值的差异显著性可得 数据如下表 5 所示 表格 5 两组品酒员对所有白葡萄酒方差分析表 方差来源 平方和 两组品酒员 0.57128 随机误差 13.1787 总和 13.7499 自由度 1 8 9 均方 0.5713 1.6473 F 0.3468 显著性 无显著差异 查表得 F0.05(1,8)=5.32>0.3468，所以我们认为在白葡萄酒的评价过程中两 组评酒员的结果也是无显著性差异的 4.1.3 对哪一组数据更可信的分析 虽然用方差检验的方法可以看出两组评酒员的瓶酒结果是无显著性差异的， 作出的折线图如下图 6、图 7 所示 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料