基于改进多目标狼群算法的微电网调度优化.pdf-资料库

c1a3553c-b3dc-4ddf-8188-7a2fc8753be3.pdf-第1页.png

第1页 / 共6页

c1a3553c-b3dc-4ddf-8188-7a2fc8753be3.pdf-第2页.png

第2页 / 共6页

c1a3553c-b3dc-4ddf-8188-7a2fc8753be3.pdf-第3页.png

第3页 / 共6页

c1a3553c-b3dc-4ddf-8188-7a2fc8753be3.pdf-第4页.png

第4页 / 共6页

c1a3553c-b3dc-4ddf-8188-7a2fc8753be3.pdf-第5页.png

第5页 / 共6页

c1a3553c-b3dc-4ddf-8188-7a2fc8753be3.pdf-第6页.png

第6页 / 共6页

基于改进多目标狼群算法的微电网调度优化基于改进多目标狼群算法的微电网调度优化为获得微电网系统建设成本、环境成本和运行成本的多重目标优化，以构建系统独立运行模块和仿真模块为核心，设计了微电网系统的多目标调度模型。使用能量模块对微电网调度模型的建设成本、环境成本和运行成本指标进行评价，优化调度算法模块则使用基于个体密度多目标狼群算法(Multi-objective wolf colony algorithm，MOWCA)。在MOWCA算法中引入了非支配排序和个体密度多样性保持操作，有效提高了多目标优化的前沿分布多样性和收敛精度。将所提优化调度算法基于Docker容器技术，对风柴蓄光微电网系统进行调度优化模拟，验证了所提调度算法在多重目标优化上的有效性。 0 引言引言微电网在现代电力中得到不断应用推广，如何获得微电网构建和运行成本经济性、环境效益最大化是非常有价值的研究方向[1-2]。而传统针对大型发电机的调度优化策略无法适应微电网复杂多目标属性。进化计算方法具有优秀全局优化性能，但初始点对算法收敛效果影响很大。文献[3]研究了具有爬坡限制条件发电机的经济性调度策略，实现算法性能提升。文献[4]提出种群多样性为策略的遗传算法改进，对建设成本、设备容量进行经济性调度。文献[5]基于梯度策略对遗传进化算法种群进行初始改进，但梯度策略需对优化目标执行求导，实现过程复杂。传统基于多目标算法的电网调度策略的设计思路是将其转化成单目标问题优化，如权重策略[6]、模糊评估策略[7]等；但附加转化过程会受主观意识左右，很难均衡各评价目标间的重要性。多目标遗传进化算法(NSGA-Ⅱ)采用精英进化方法，并利用非支配形式的排序策略进行个体隶属关系比较，是一种常用的多目标优化方法。狼群算法[8]是一种在连续空间内采取随机方式进行启发式优化的搜索方法，在算法结构上与遗传算法近似，但无需编码、解码过程，因此具有算法实现简单、运行和收敛速度快的优点。本研究建立了微电网多目标调度优化模型，并采用基于个体密度多目标狼群算法进行求解。改进算法引入了非支配排序和个体密度多样性保持操作，有效提高了多目标优化的前沿分布多样性和收敛精度。 1 系统模块系统模块 1.1 模块结构设计模块结构设计本研究模块调度优化结构如图1所示。图1所示的调度模块设计方法包含输入、输出、系统仿真和调度优化4个模块，相互之间通过数据交流进行目标的优化。其中，输入部分的作用是向系统中输入参数数据；输出部分包含调度优化目标值和最终的实施方案；调度优化模块和系统模型是所设计调度模块的核心，基于两个模块之间信息交流实现目标的调度优化。其中，上述系统模型基于能量模型进行准稳态特性下的系统仿真运行，并评估所设计方案的经济和环境性；采用优化方法实现调度策略的优化设计，调度优化模块利用种群对调度方案进行学习和指标评估，并以适应值形式进行模块优化值传递。 1.2 运行约束条件运行约束条件微电网系统运行约束主要是功率均衡方程：

1.3 调度优化多目标模型调度优化多目标模型调度优化多目标模型可表示成下列计算方式：式中，fi为优化目标i，X为需优化微电网变量，G为等式约束，H为不等式约束，Ω为解空间。微电网调度优化目标为： 2 微电网微电网MOWCF多目标调度优化多目标调度优化 2.1 狼群算法狼群算法狼群算法（WCA）主要是通过对群狼捕猎行为的协作模拟实现目标的优化，见图2。 WCA算法中，群狼分工明确，有猛狼、探狼和头狼之分，其中头狼的目标函数值最优，气味浓度是目标适应值。算法步骤如下： (1)对人工狼位置初始化Xi，设定探狼游走次数上限Tmax，狼群规模N，探狼比重α，迭代数上限kmax，比例更新因子β，步长因子S，距离因子w。 (2)选取头狼并选择S_num探狼游走，如浓度Yi优于头狼浓度Ylead，或游走数达最大值Tmax，则跳转步骤(3)。 (3)猛狼围捕猎物，如探测到浓度YiYlead，那么猛狼继续围捕，直到满足dis=dnear，则跳转步骤(4)。

(5)按优胜劣汰方式进行头狼位置更新，按照强者保留原则进行狼群个体更新。 (6)判定是否达到终止条件，如满足则终止，并输出头狼信息，获得最优解，否则跳转步骤(2)。 2.2 非支配个体选取非支配个体选取这里设计了一种非支配快速排序选择方法： (1)对狼p操作：①设定Sp=φ，np=0，Sp储存个体p支配个体，np为支配个数；②如满足p>q，那么令Sp=Sp∪{q}；否则 q>p，np=np+1； ③若满足np=0，那么狼p等级prank=1，然后把p加入Pareto前沿集合内，F1=F1∪{p}； (2)满足Fi=φ前，对算法执行操作：①设定Q=φ，对Fi临时存放；②对Fi内狼p进行操作：对Sp内狼q，令nq=nq-1，若满足 nq=0，那么q仅受p支配，Q=Q∪q，qrank=i+1；③设定i=i+1；④设定Fi=Q，并获得前沿集F2～Fn。 2.3 个体密度计算个体密度计算对r个目标f1、f1…fr，狼i个体密度为P[i]dis，那么可得个体密度值计算形式为：对于大小为N的狼群，最差情况对r个目标密度计算复杂度为O(rN)，排序复杂度为O(rNlogN)，则总计算复杂度是 O(rNlogN)。 2.4 微电网多目标调度算法微电网多目标调度算法多目标狼群微电网标调度算法如图3所示。图3中，选取N/2个体构建猛狼子群，通过围捕和更新生成狼群p1，并与狼群p混合，执行非支配选取和个体密度计算，获得规模为N的新狼群p′。 3 实验分析实验分析 3.1 性能测试性能测试所选用的测试函数形式为：

式中，向量x的区间为0≤xi≤1。设定参数N=200，Tmax=500，α=0.25，β=0.1，S=0.01，w=0.01。对比算法：NSGAⅡ、VEGA、SOEA[8]和SPEA算法，对比结果见图4。图4(a)~图4(b)分别是算例1~2的Pareto前沿解集的对比情况。根据图4实验结果可看出，在前沿性指标上，本文算法要优于选取的NSGAⅡ、VEGA、SOEA和SPEA 4种算法，在均匀性指标上，本文算法要显著好于SOEA和VEGA两种算法，略好于 SPEA和NSGAⅡ两种算法。 3.2 微电网算例优化微电网算例优化 Docker容器技术与传统虚拟技术的差别在于其直接对虚拟化过程进行操作系统层面操作，可实现系统内核共享。不存在额外的中间层的计算开销。由此可知，Docker容器技术具有非常高的资源利用率和执行效率。这里以Garver-14节点的风柴蓄光微电网系统为算例，采用Docker容器技术进行算法性能验证。各设备单元的具体参数如表1所示。

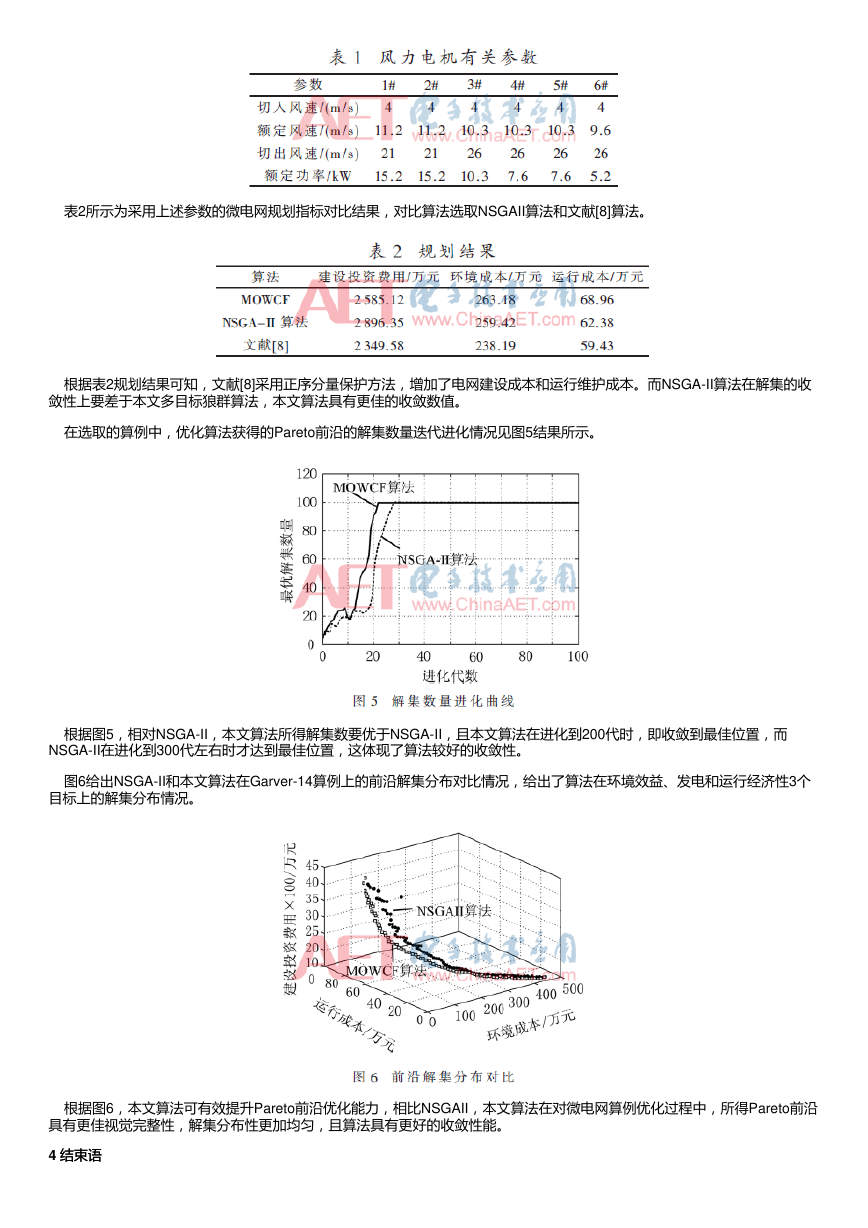
表2所示为采用上述参数的微电网规划指标对比结果，对比算法选取NSGAII算法和文献[8]算法。根据表2规划结果可知，文献[8]采用正序分量保护方法，增加了电网建设成本和运行维护成本。而NSGA-II算法在解集的收敛性上要差于本文多目标狼群算法，本文算法具有更佳的收敛数值。在选取的算例中，优化算法获得的Pareto前沿的解集数量迭代进化情况见图5结果所示。根据图5，相对NSGA-II，本文算法所得解集数要优于NSGA-II，且本文算法在进化到200代时，即收敛到最佳位置，而 NSGA-II在进化到300代左右时才达到最佳位置，这体现了算法较好的收敛性。图6给出NSGA-II和本文算法在Garver-14算例上的前沿解集分布对比情况，给出了算法在环境效益、发电和运行经济性3个目标上的解集分布情况。根据图6，本文算法可有效提升Pareto前沿优化能力，相比NSGAII，本文算法在对微电网算例优化过程中，所得Pareto前沿具有更佳视觉完整性，解集分布性更加均匀，且算法具有更好的收敛性能。 4 结束语结束语

本文采用MOWCA算法进行了风柴蓄光微电网系统多目标规划，该模型考虑到了微电网设计的环境效益和经济型成本，并对算法引入了个体密度计算和非支配个体选取过程，有效增加了种群进化的多样性能，获得了更好的收敛性能，本文的规划方法可为微电网设计提供解决思路。参考文献参考文献 [1] 郭筱瑛，王嘉磊，黎凡森，等.基于VSG的LCL型微网逆变器技术研究[J].电子技术应用，2017，43(1)：152-155，160. [2] 陈西，付蓉.并网模式微电网双层分布式优化调度算法[J].微型机与应用，2016，35(7)：79-82. [3] VRIONIS T D，KOUTIVA X I，VOVOS N A.A genetic algorithm-based low voltage ride-through control strategy for grid connected doubly fed induction wind generators[J].IEEE Transactions on Power Systems，2014，29(3)：1325-1334. [4] ROSTAMI N， FEYZI M R，PYRHONEN J，et al.Genetic algorithm approach for improved design of a variable speed axial-flux permanent-magnet synchronous generator[J].IEEE Transactions on Magnetics，2012，48(12)：4860-4865. [5] SAMARAWICKRAMA K，JACOB N D，GOLE A M，et al.Impulse generator optimum setup for transient testing of transformers using frequency-response analysis and genetic algorithm[J].IEEE Transactions on Power Delivery，2015，30(4)：1949-1957. [6] Li Haiyan， Ma Mingxu，Zhang Wenlei.Multi-objective collaborative optimization using linear physical programming with dynamic weight[J].Journal of Mechanical Science and Technology，2016，30(2)：763-770. [7] 李国亮，魏振华，徐蕾.基于改进搜索策略的狼群算法[J].计算机应用，2015，35(6)：1633-1636，1687. [8] MIRSAEIDI S，SAID D M，MUSTAFA M W，et al.A protection strategy for micro-grids based on positive-sequence component[J].IET Renewable Power Generation，2015，9(6)：600-609. 作者信息：作者信息：马文1，耿贞伟1，张莉娜1，于凤荣2 （1.云南电网有限责任公司信息中心应用技术部，云南昆明650217； 2.昆明理工大学冶金与能源工程学院，云南昆明650093）

资料库

基于改进多目标狼群算法的微电网调度优化.pdf

相关推荐

开发技术

热门标签

最新资料